双臂空间机器人闭链系统的协同柔顺控制策略研究

原劲鹏, 葛连正, 李德伦

1.北京空间飞行器总体设计部, 北京 100094 2.哈尔滨工业大学, 哈尔滨 150001

0 引 言

多臂空间机器人协调操作是机器人学非常重要的研究方向,许多关键技术问题还处于探索和仿真阶段[1-4].空间协作机器人和目标的闭合系统末端与目标之间不存在相对运动,目标、协作机器人和基座需要满足闭链运动约束[5-6].同时,整个系统不受外部力和力矩作用,基座、机器人和目标的速度满足线动量和角动量守恒约束[7].为了保证在调整目标位置过程不损坏目标或者机器人末端工具,需要调节机器人末端施加在目标上的作用力.此外,在调整目标位置的过程中应尽量减少对基座姿态的扰动.

闭链机器人系统控制过程中既存在闭链约束几何关系又存在抓持内力的均衡配置问题,即表现为力/位置混合控制问题[8-11];在漂浮基闭链多臂空间机器人系统中还有耦合系统动量及动量矩守恒关系,其控制系统设计问题更难.针对协同移动同一目标这一任务,主要有外力/目标柔顺[12-14]、内力/机器人末端柔顺[15-17]和关节柔顺机制[18-20]3种柔顺机制.其中,外力/目标柔顺机制是建立反作用力和目标位姿之间的关系,将空间机器人动力学方程融合进目标动力学方程中,针对得到目标动力学方程设计柔顺控制器,不足在于需要目标精确的运动学和动力学参数;内力/机器人柔顺机制是建立内力与机器人末端位姿的关系,其优点是不需要考虑目标的运动学和动力学模型;关节柔顺机制就是将内力/机器人柔顺机制中的机器人位姿信息表示为关节角的相关信息.关节柔顺机制只能在电流控制环级实现,而内力/机器人柔顺机制可以在位置和速度控制环级实现.

本文以双臂六自由度空间机器人为研究对象,针对双臂移动空间目标的运动控制进行研究.首先进行了双臂空间机器人的闭链分析和动力学建模,然后基于外力/目标柔顺控制机制,引入虚拟铰接机构,采用弹簧+阻尼结构将操作目标和机械臂断开,并转化为有约束限制的多体动力学问题进行了机器人协同柔顺控制器设计,最后进行了仿真验证.

1 双臂空间机器人闭链系统模型

1.1 闭链系统描述

空间双臂机器人和捕获目标的闭链系统如图1所示,包括基座、操作臂、协作臂和捕获目标等部分,操作臂和协作臂各为6个自由度.

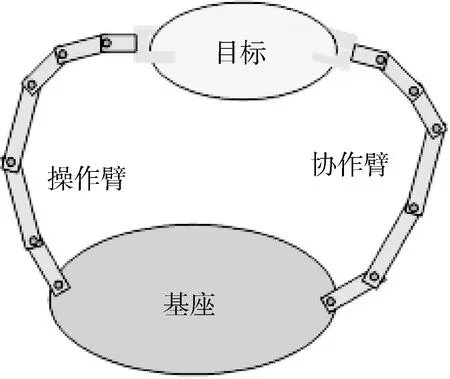
图1 闭链系统示意图

为了便于对闭链系统的运动学和动力学模型进行分析,假设双臂空间机器人和操作目标闭链系统满足如下的约束:

1)手爪和目标之间不存在相对运动时,基座、机器人和目标构成闭链系统。

2)整个闭链系统不受任何外部力和力矩的作用,也即闭链系统的线动量和角动量守恒.

1.2 闭链系统动力学模型

操作臂/协作臂的第i个刚性连杆受到的力和力矩可以迭代地表示为

(1)

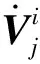
利用式(1),可得下面的关系

(2)

(3)

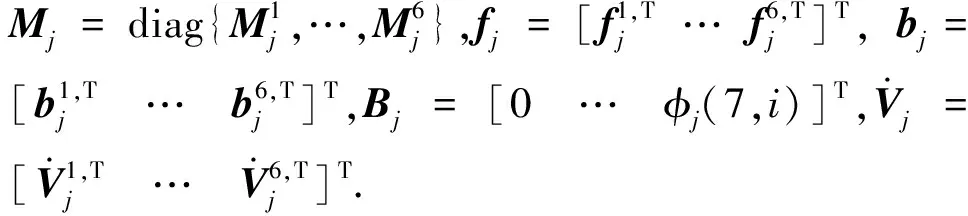
(4)

由于整个系统不受到任何外力和外力矩,因此基座航天器的力和力矩平衡方程为

(5)

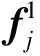
(6)

操作/协作臂各连杆的空间速度表示为

(7)

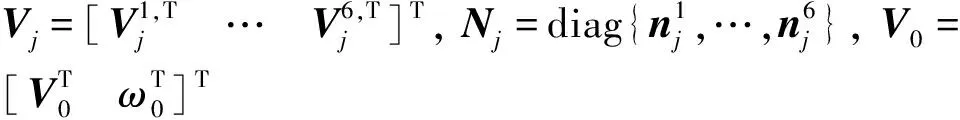
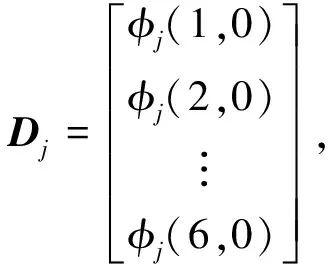
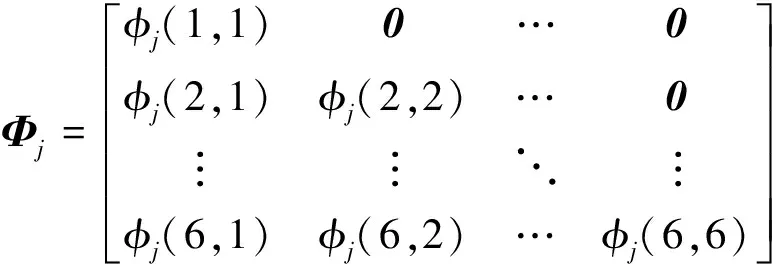
对式(7)关于时间求导,利用矩阵N为常矩阵的事实,可得

(8)

当闭链系统的初始动量为零时,可以得到基座速度和关节角速度之间的关系,即

(9)

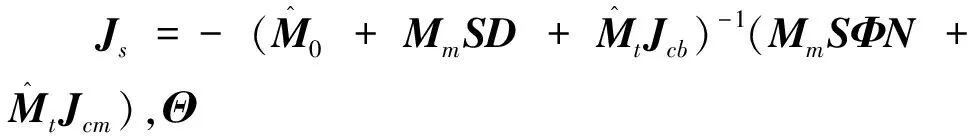
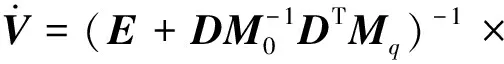
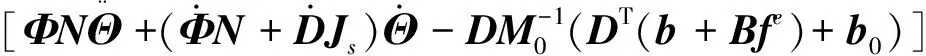
(10)

将式(10)代入式(4),对所得方程式进行整理,可得空间双臂机器人的动力学方程为

(11)

其中,

τ=NTf为各关节处的控制力矩.

此外,目标的动力学方程为

(12)

其中,Mt是目标的广义惯量矩阵,Ct是向心力和科氏力项,W=[EE]T,Jce=diag{Jce1,Jce2}.

2 协同柔顺控制器设计

双臂空间机器人在夹持移动同一目标物体的过程可以由受到外力作用的空间机器人的动力学方程结合目标的动力学方程来描述.同时,两者在夹持点处满足刚性夹持的约束条件,即两者在接触点处的速度相同.为了保证在移动过程中既能保持目标与基座的相对位姿关系,又不破坏闭链约束条件,需要一臂刚性地移动目标以维持相对位姿关系,另一臂以柔顺的方式进行协同运动避免破坏闭链约束关系.因此,整个移动过程中,需要在一个接触点处引入一个虚切断铰接结构.虚切断铰接是在双臂闭链系统中引入虚拟的铰接,采用弹簧加阻尼结构将操作目标和机械臂断开,从而可将双臂机器人协调问题转化为有约束限制的多体动力学问题.

协同柔顺控制问题的核心就是设计合适的柔顺机制建立力偏差与加速度偏差、速度偏差以及位置偏差之间的关系.通常,这种关系可以表示为

(13)

这里,δx=xd-xr为期望位姿与输入到位置控制回路中的参考位姿之间的偏差,δF=Fd-F为期望力和力矩与真实力和力矩之间的偏差,M、B、K分别为正定的惯量、阻尼和弹性系数矩阵.由式(13)可知看到,柔顺机制可以看作是一个二阶滤波器,滤波器的输入是力和力矩偏差,输出是对期望位姿的一个修正值δx.

2.1 系统柔顺控制器

针对基座自由漂浮机器人协同移动目标运动的任务,本文提出如图2所示的协同柔顺控制器.整个协同移动控制的实现机制为

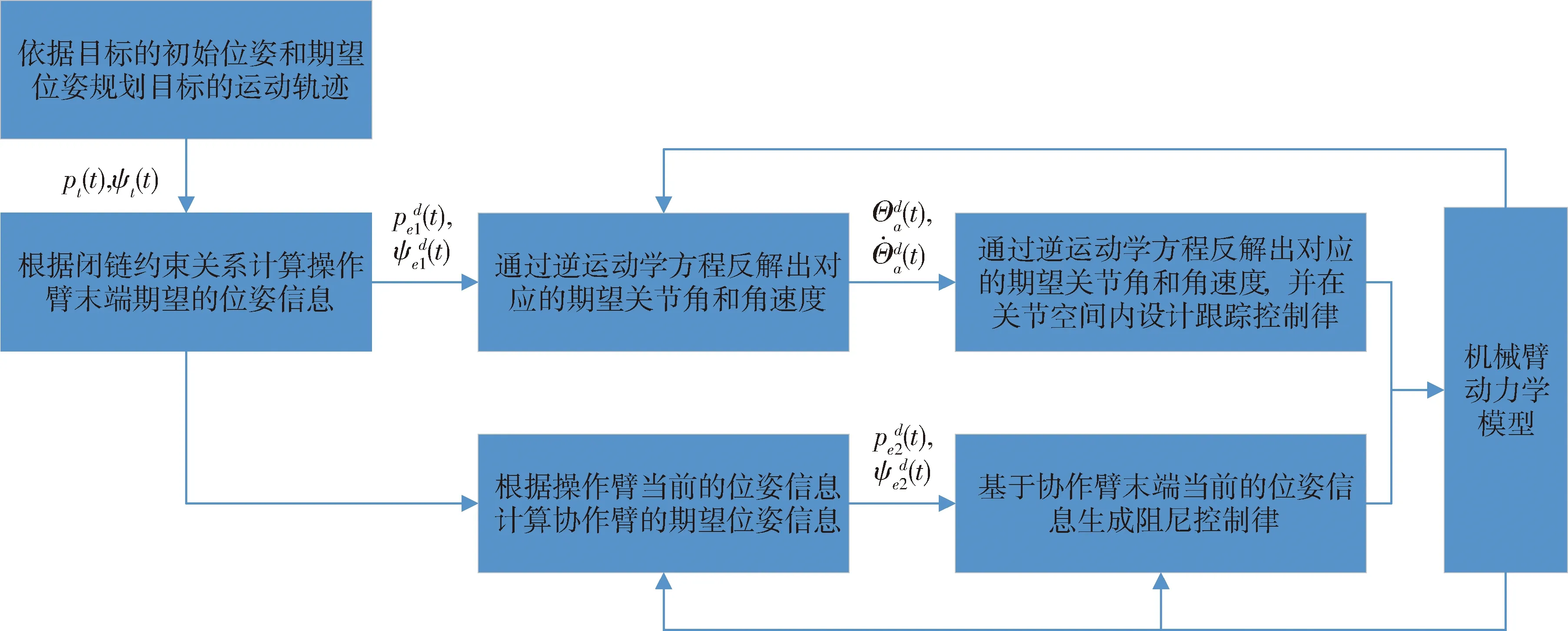
图2 柔顺控制结构示意图

1)依据目标的初始位姿和期望位姿规划目标的期望运动轨迹,并基于闭链约束条件设计操作臂的运动轨迹和跟踪控制律;

2)基于目标的尺寸信息和操作臂末端的位姿,生成协作臂末端的期望位姿信息;

3)基于式(13)得到位姿偏差信息对期望轨迹进行补偿,最后实现协同移动作业任务.

2.2 目标位置和姿态运动规划

设目标坐标系相对于基座坐标系的初始位置和姿态矩阵分别为pt(0)和Rbt(0),目标期望位置和姿态矩阵分别为pt,d和I3×3.目标位置的运动由梯形速度法进行规划,设定目标期望加速度为at,m,最大速度为vt,m,目标期望运动轨迹为

(14)

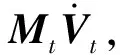
考虑目标动力学方程式(12),机器人对目标的作用力可以分解为

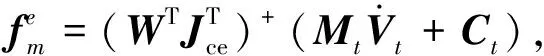
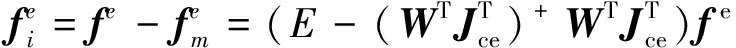
(15)

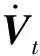
2.3 操作臂关节角和角速度的跟踪控制器设计

操作臂末端速度和抓捕点处的速度满足如下的关系:

(16)

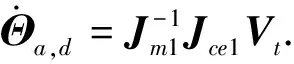
(17)

其中,Ma是维度(3×18)的机器人子系统的广义惯量矩阵,依次包括机械臂的6个杆件惯量参数.fe1为目标对操作臂的作用力.因此设计控制力矩为

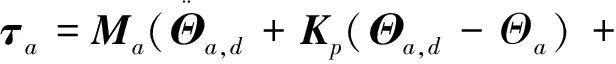
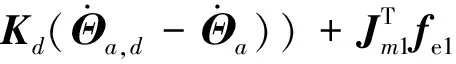
(18)

2.4 协作臂协同控制律的设计

假设两个抓捕点之间的位置矢量为l,根据当前操作臂末端在基座坐标系下的位姿信息,可以得到期望的协作臂末端的位姿信息分别为

pb,d=pa+Ral,Rb,d=f(Ra)

(19)

式中,f(Ra)由具体的闭链拓扑构型决定.记协作臂末端当前的位置和姿态信息分别为pb和Rb,设计协作臂的控制律为

(20)

其中,X和Xd分别是协作臂末端相对于基座坐标系的真实和期望位姿参数化表示,δX=X-Xd.

2.5 稳定性证明

令eΘ=Θa-Θa,d,选取Lyapunov函数为

(21)

对式(21)关于时间求导,可得

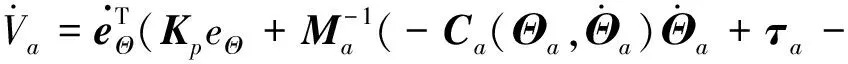
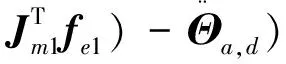
(22)

将控制律(18)代入式(22),可得

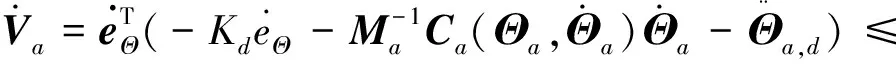
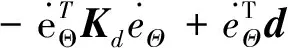
利用Young不等式,可得

对于协作臂而言,其末端的运动学方程和动力学方程分别为

(23)

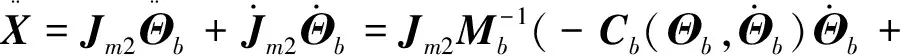
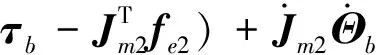
(24)

将协同控制律(20)代入(24),可得

(25)

由式(25)可知,当选取合适的矩阵M、B、K可以保证各通道的二阶系统是稳定的.

3 仿真实验

3.1 数值仿真

设双臂机器人和目标的初始构型如图9所示,目标为800 mm立方体,基座为2 000 mm×2 000 mm×3 000 mm的长方体,系统仿真参数如表1.

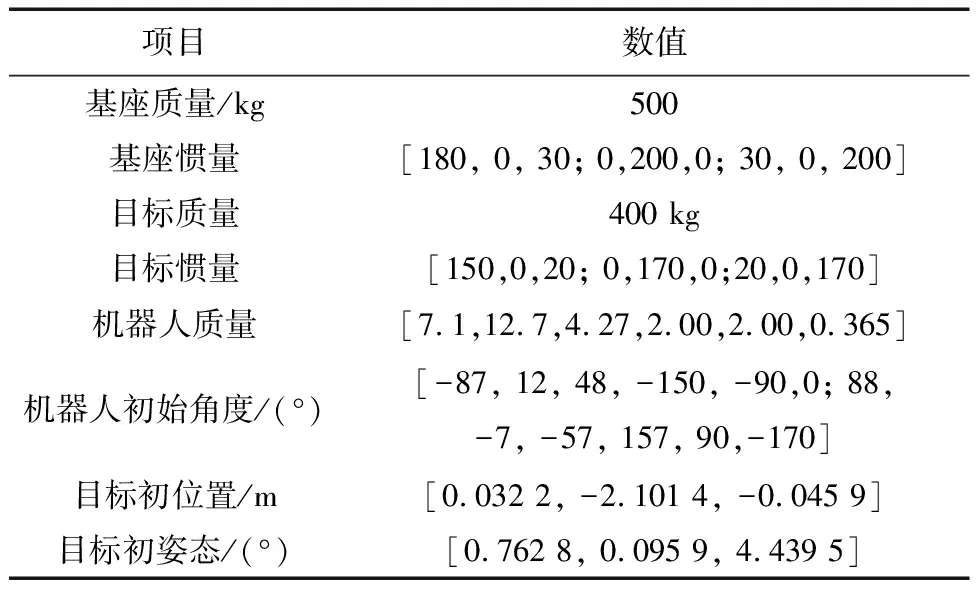
表1 系统仿真参数

设定目标在基座坐标系中期望的停靠位置和姿态分别为bpt,d=[0 -1.65 0]m和I3×3.抓取点在目标中位置分别为:tph1=[-0.413 0.487 0.013]m,tph2=[0.416 0.484 0]m.对应的雅克比矩阵为

目标的相对平动运动选取加减速时长为10 s,最大平动速度为0.04 m/s.为了保证目标坐标系指向和基座坐标系对齐,设计目标的角速度为

ωt=0.5(abt×e1+obt×e3)

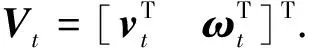
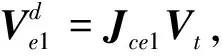
其中,M1为操作臂的广义惯量系数矩阵,Kp和Kd分别为正定对称增益矩阵.

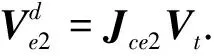
也即两者之间的作用关系由一个阻尼器和一个弹簧来模拟,式中Km和Kb分别为环境的阻尼系数和刚性系数.设计柔顺控制律为

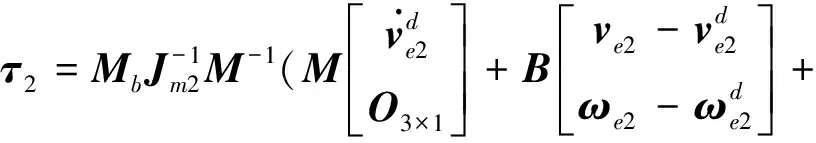
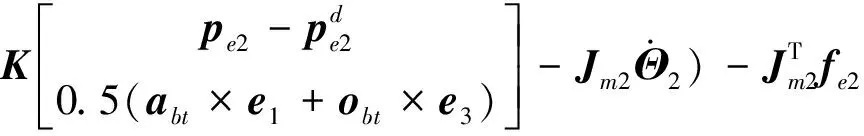
其中,M2为协作臂的广义惯量矩阵,M、B、K分别为柔顺控制律中的质量、阻尼和刚性系统矩阵.

根据以上条件,双臂空间机器人对目标的操作仿真结果如图3～7所示.其中,图3为机器人在基座坐标系中的运动轨迹;图4为双臂操作目标时操作臂和协作臂的运动轨迹偏差仿真,仿真结果表明双臂操的轨迹偏差小于3 mm,可实现双臂的协同柔顺控制.图5和图6分别为操作臂和协作臂关节控制力矩的轨迹;图7为基座质心位置和欧拉角的运动轨迹,可以发现自由漂浮基座的位置和姿态会受机械臂运动的影响.

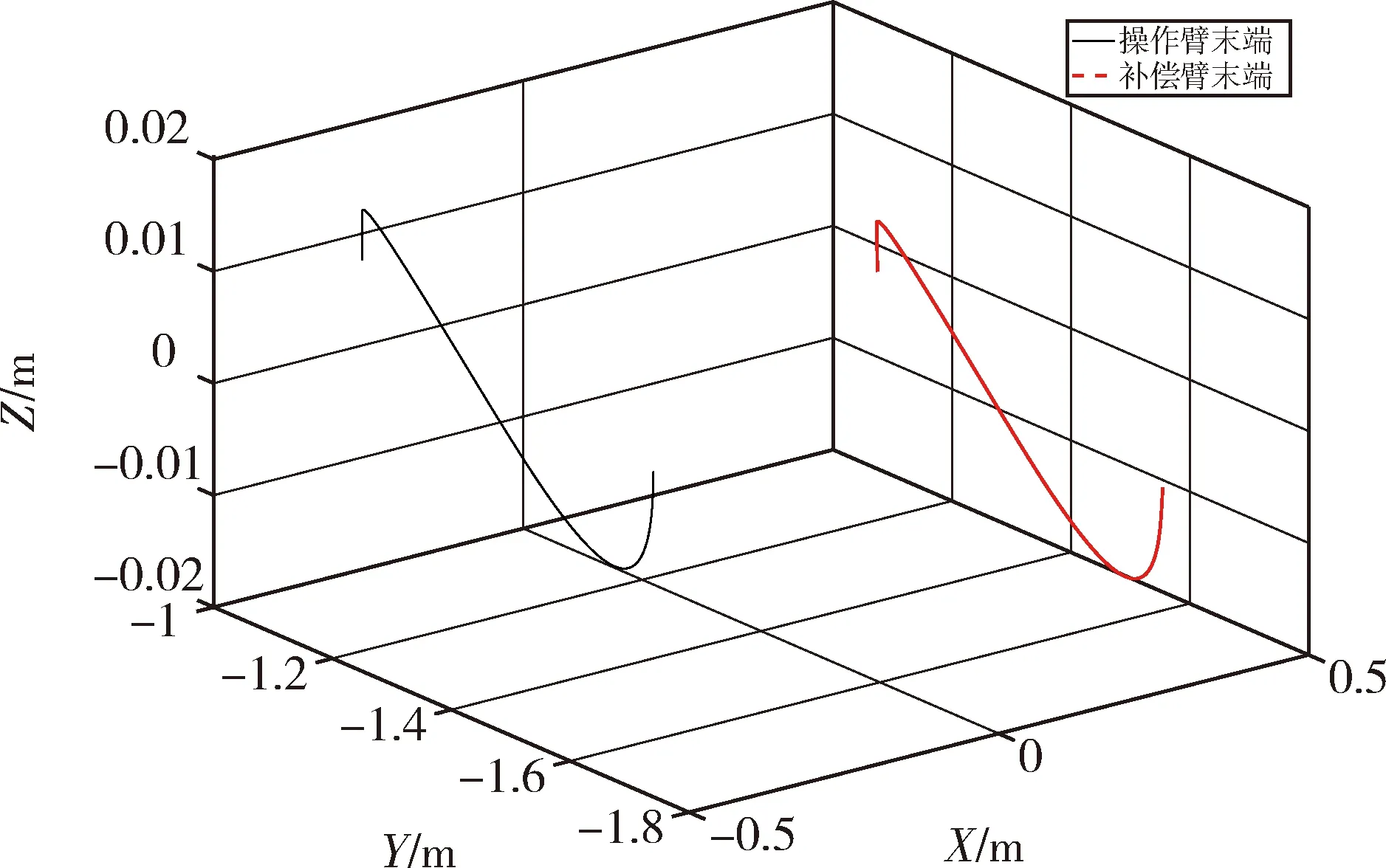
图3 机器人末端的位置运动轨迹

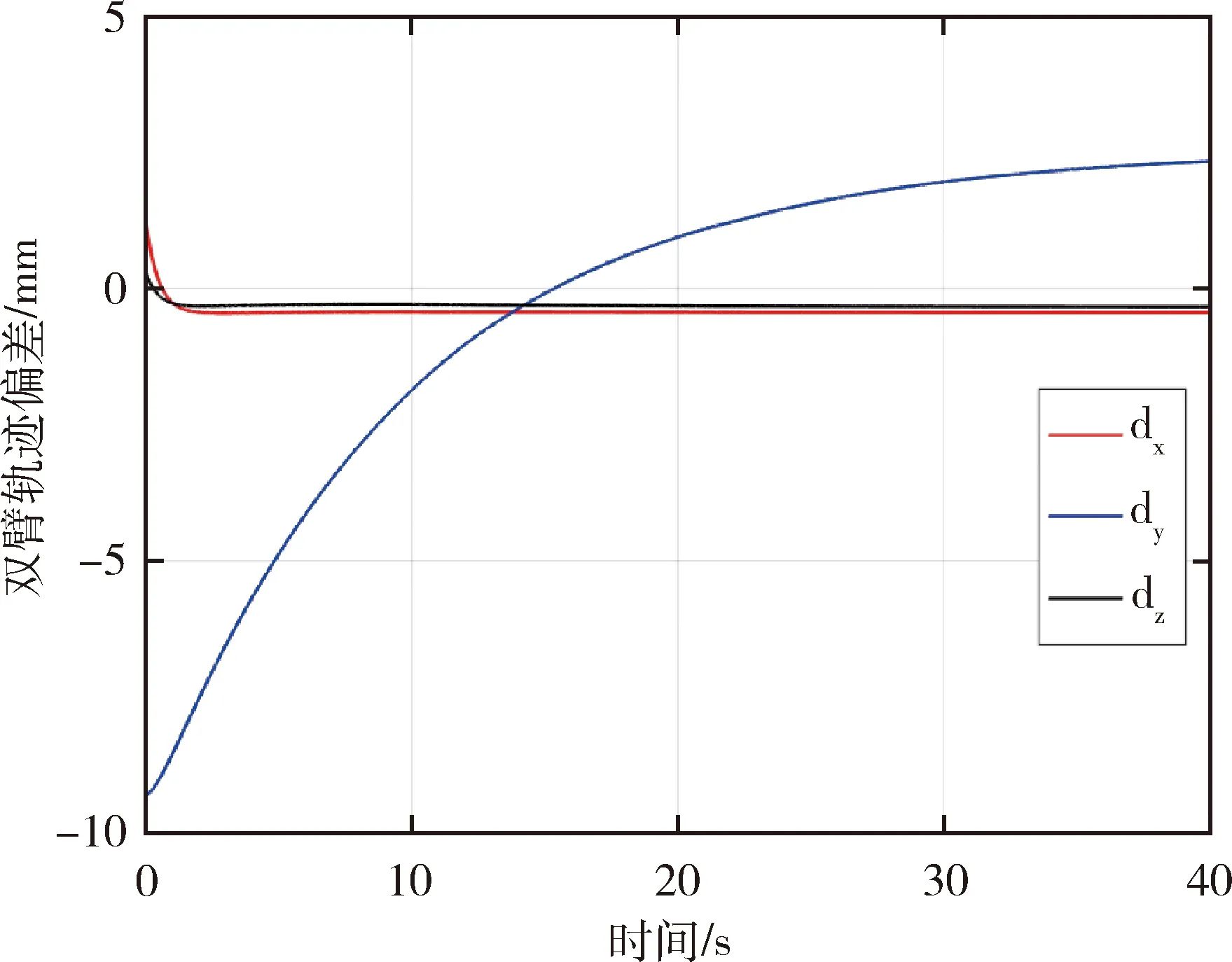
图4 双臂机器人末端操作轨迹偏差

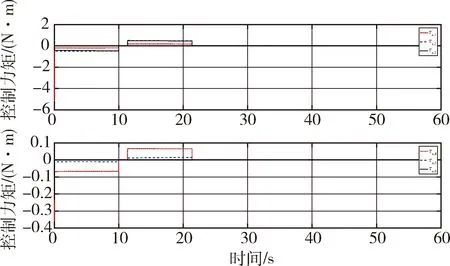
图5 操作臂的控制力矩

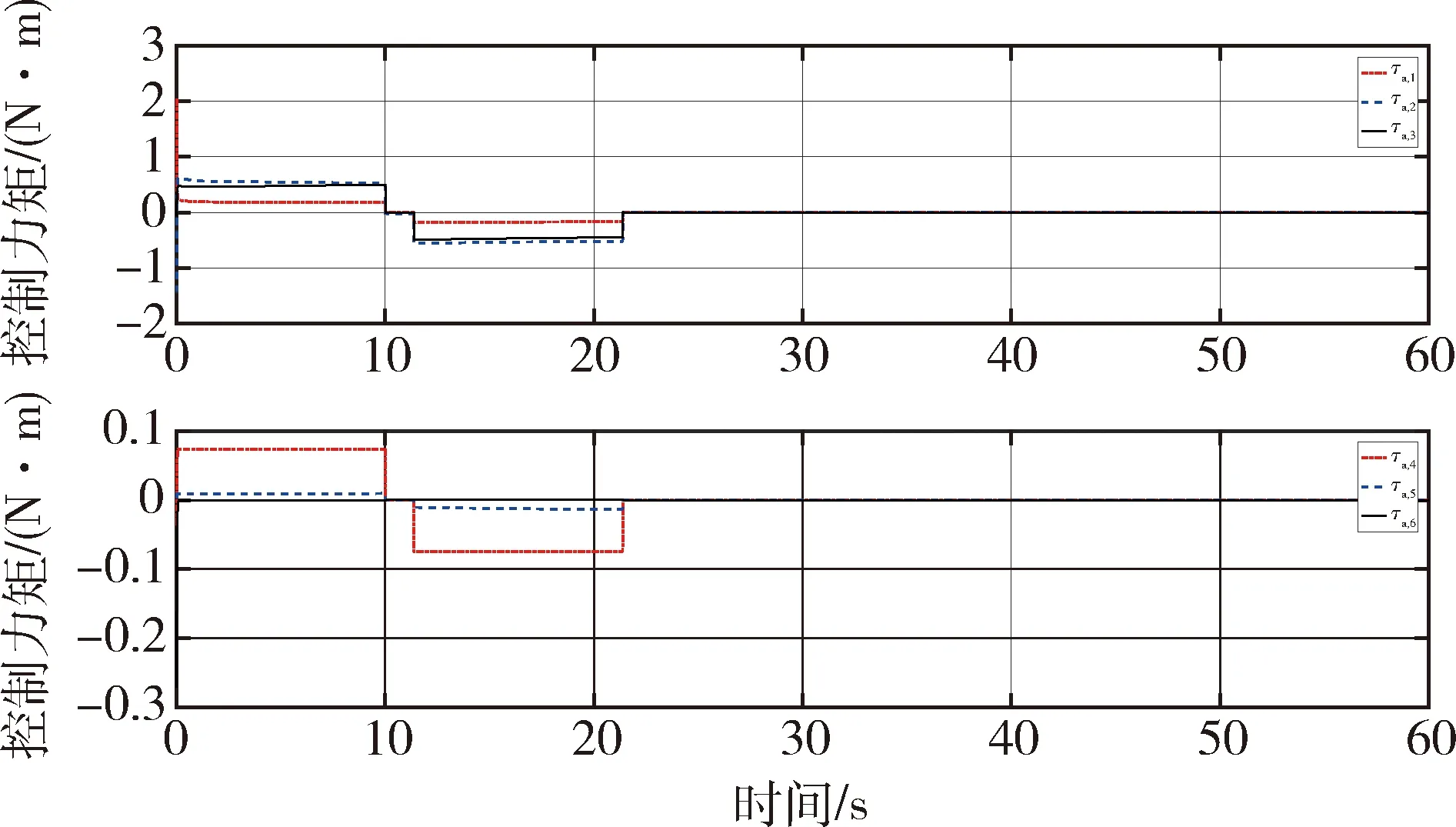
图6 协作臂的控制力矩

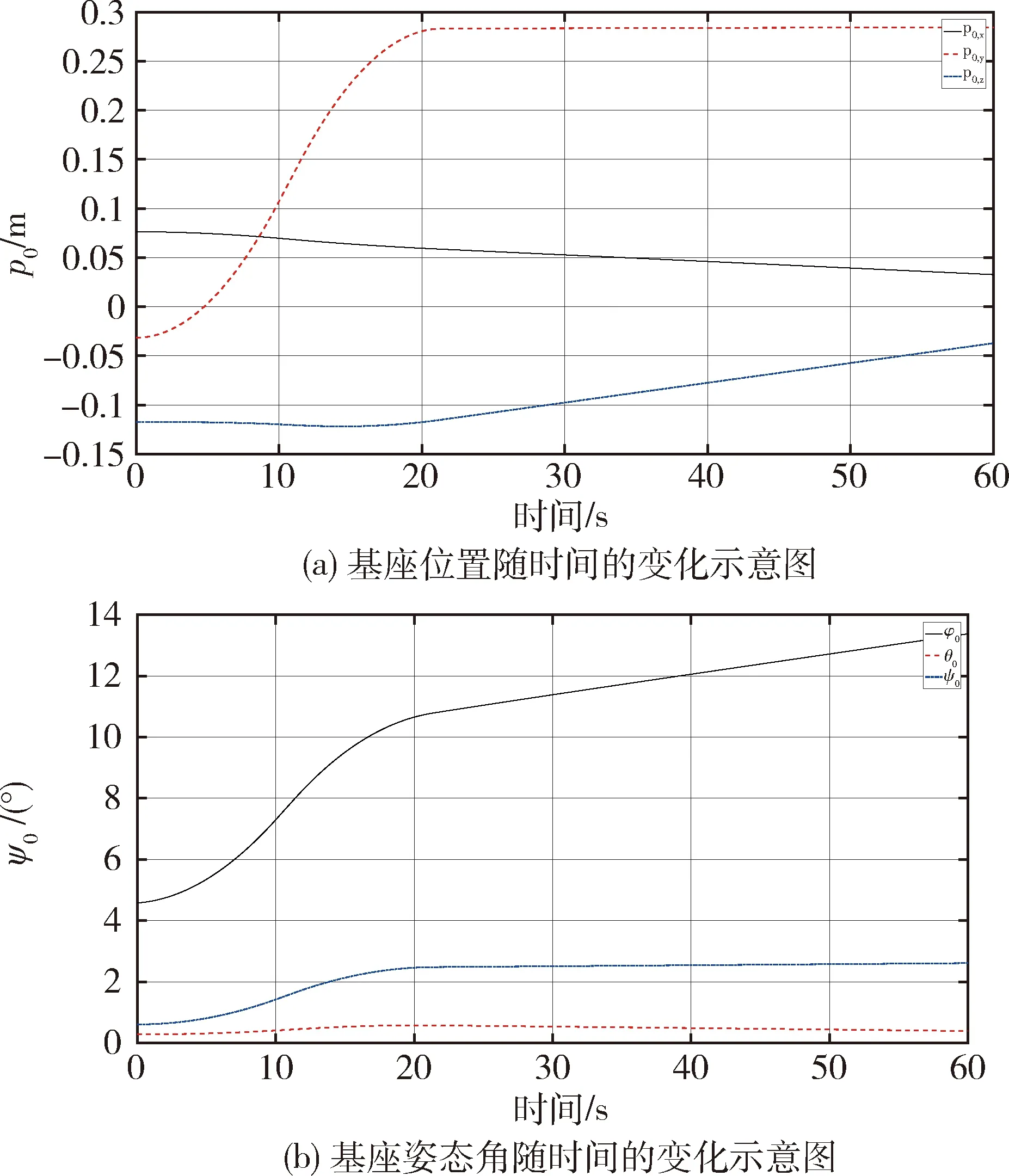
图7 基座位姿随时间的变化示意图

3.2 ADAMS仿真

为了验证所设计的协调柔顺控制器的效果,搭建闭链系统的ADAMS虚拟样机如图8所示.由ADAMS输出的目标质心相对于基座坐标系的位置以及目标坐标系相对于基座坐标系的欧拉角分别如图9和图10所示.

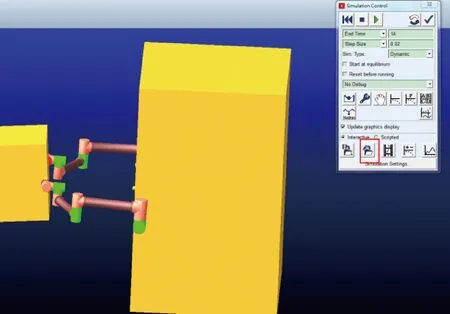
图8 机器人系统ADAMS模型

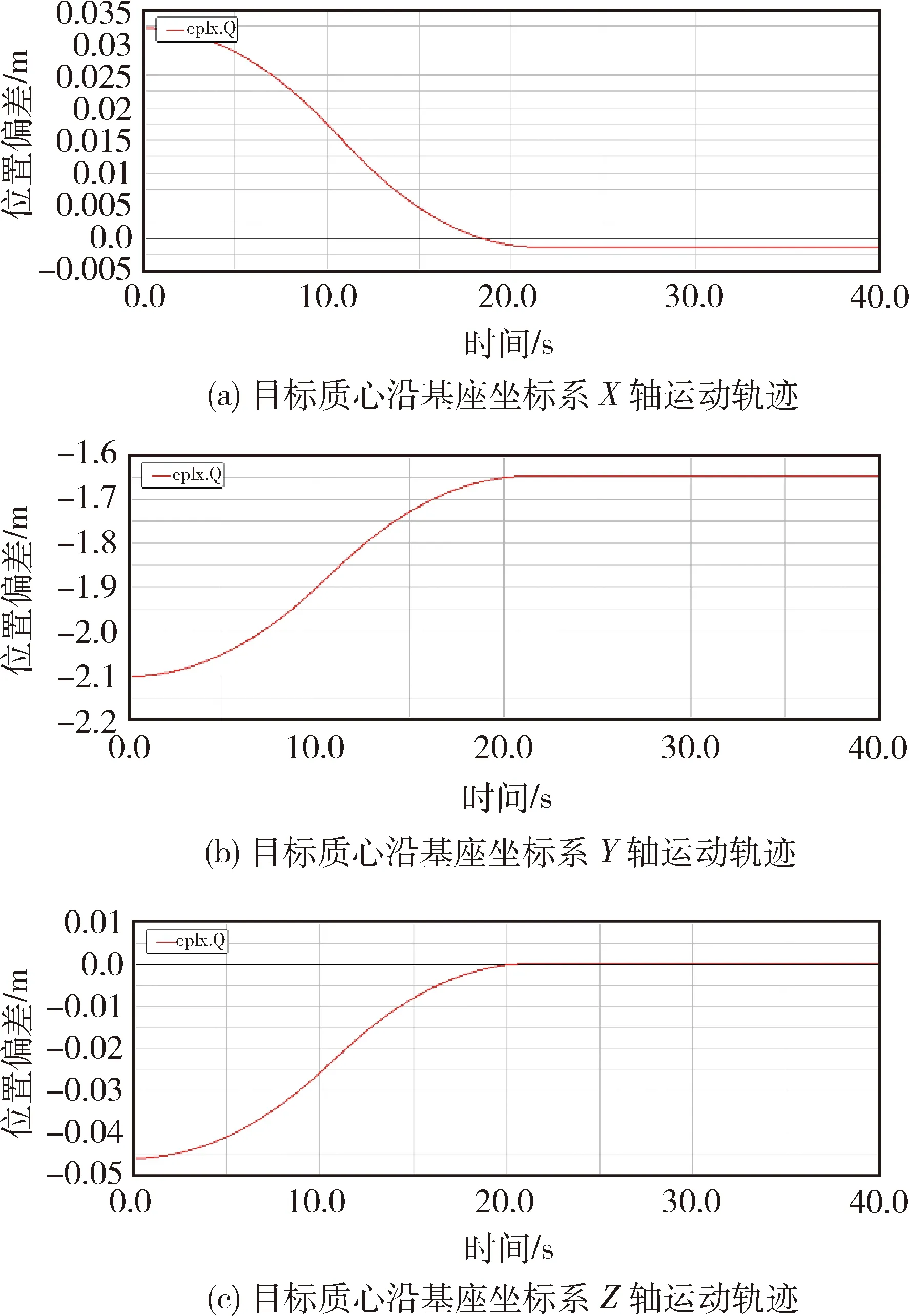
图9 目标质心沿基座坐标系的运动轨迹

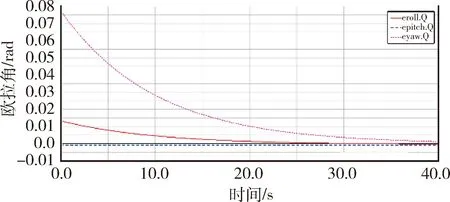
图10 目标坐标系的欧拉角运动轨迹

由仿真结果可知,在协调运动控制律的作用下,双臂能够以较高的指向精度将目标移动到期望的位置处.

仿真运动结束后,目标坐标系相对于基座坐标系的位置和旋转矩阵分别为:bpt=[-0.001 2-1.647 4 0.000 3]T,Rbt=I3×3,与期望的位置和姿态误差满足要求.

4 结 论

针对双臂空间机器人对目标的协同操作任务,本文基于闭链系统的动力学模型,设计了以操作臂刚性移动目标以保证目标和基座的相对位姿关系,协作臂柔顺的改变自身的关节构形以保证闭链系统的约束不被破坏的协同操作模式.对操作臂和协作臂分别设计了刚性的关节跟踪控制律和柔顺阻尼控制律,仿真结果表明该控制算法可以实现协调移动目标到达基座坐标系中预设的期望位置的任务,能够满足空间双臂机器人的目标移动要求.