月面起飞快速交会远程导引制导律设计
王高阳, 胡海霞*, 解永春, 刘 涛
1.北京控制工程研究所, 北京 100094 2.空间智能控制技术重点实验室, 北京 100094
0 引 言
近年来,载人登月作为载人深空探测的热点方向,得到了世界大国的普遍关注.2022年12月11日,美国Artemis 1号的猎户座飞船经过绕月飞行后成功返回[1],这是继Apollo计划后,美国拉开了新一轮的载人登月活动的序幕.中国通过嫦娥工程的系列探测器,完成了无人月球“绕、落、回”探测任务,下一步载人登月的相关论证工作已经展开.在环月轨道建立中转站,通过月球轨道交会对接(rendezvous and docking, RVD)的方式可以大幅度减小从地球或月球发射航天器的规模,有效降低对起飞运载能力的需求.因此,月球轨道交会对接技术是实施载人登月以及载人深空探测的关键技术之一[2].
交会对接的过程从距离上讲是一个由远到近的过程,从精度上讲是一个由粗到细的过程[3],整个过程可以分为两个阶段:1)远程导引段是指将航天器从初始轨道导引到近距离自主控制段所需要的预定轨道,为了保证任务的快速性,部分工程将远程导引终点设计在距目标器十公里左右的位置处;2)近距离自主控制段是指从航天器之间建立相对导航开始,通过自主实施姿态和轨道控制,直至对接的过程,任务设计的重点是控制精度和安全性[4].工程任务中远距离导引策略分为两类,一类是以美国航天飞机交会策略为代表的特殊点变轨策略,面内变轨在远地点或近地点,面外变轨采用独立脉冲进行控制;另一类是以俄罗斯联盟号飞船交会策略为代表的综合变轨策略,该策略的核心算法是由BARANOV[5]提出的基于状态变量形式的近圆偏差线性动力学方程,每次变轨不局限于面内和面外,变轨位置也不固定,实现轨道参数与变轨速度增量联合优化的目的[6-7].月球轨道的交会对接任务也是基于这两种策略进行研究和实施的.Apollo11~12采用共椭圆交会的特殊点变轨方案,Apollo14之后采用基于Lambert变轨的综合变轨策略[8].我国的嫦娥五号远程导引轨道设计采用基于特殊点变轨的四脉冲方案[9-10].
由于载人登月任务对时间周期具有严格的要求,载人飞船必须具备快速远程交会的能力.陈欢等[11]以共椭圆快速交会为标称策略,在考虑不同约束下给出了时间最优和燃料最优的共椭圆快速交会策略.祝海等[12]设计了环月轨道一天快速降轨交会任务的调相变轨方案,采用四脉冲修正特殊点变轨算法对变轨脉冲进行求解.孟占峰等[13]基于近圆偏差方程,以纬度幅角为规划变量对月球轨道交会的四个脉冲进行规划,将交会策略设计问题转化为约束优化问题进行求解.JIANG等[14]基于Lambert方程,运用有序鲸鱼优化算法对轨道交会所需时间以及速度增量进行优化求解.SHIRAZI等[15]基于Lambert理论,设计了进化离散化Lambert方法,在时间限制、燃料限制以及脉冲限制等约束下能够找到远程导引的最优解.SAMSAM等[16]利用轨道要素方程,考虑到转移轨道平滑性、追踪性以及最优性,运用多目标非受支配排序遗传算法对远程导引变轨的脉冲进行求解.综合国内外的文献来看,对快速交会问题的处理,大多是将其转化为非线性规划问题进行求解.即在给定的时间约束、终端约束以及其他的约束下,基于制导方程,利用优化算法对满足约束条件的脉冲大小以及脉冲施加位置进行求解.目前,在快速交会的问题中大多直接对航天器的位置和速度进行规划,这些方法虽然数值精度高,但是求解过程中较为复杂.而在航天器的工程设计中,通常以摄动(机动)加速度表示的高斯方程来研究轨道机动推力对航天器轨道的影响,这种用轨道根数的变化描述航天器的运动的方法比直接用航天器的位置和速度作为因变量的方法要简便很多[17-18].高斯摄动方程在航天器轨道控制的应用研究主要集中在航天器的编队飞行中,如文献[19-20]基于高斯摄动方程,运用轨道要素偏差的方法对卫星的编队构型进行控制.在远程交会中相比于卫星编队飞行中从星轨道要素的改变量,远程交会中追踪器轨道要素的改变量非常大,使用轨道要素偏差的方法对追踪器进行控制会产生较大的误差,另外,时间约束也是快速远程交会中必须要考虑的问题.
本文以载人登月任务中月面起飞后的快速交会对接为研究背景,以登月舱作为追踪器,以飞船作为目标器,研究高斯摄动方程在快速交会远程导引段中的应用.本文首先基于高斯摄动方程推导了近圆轨道下轨道要素的脉冲控制模型,然后结合远程导引的时间约束方程设计了双脉冲的远程导引策略,为了获得最小速度增量解,通过设计规划变量,把非线性方程组的求解问题转化为了非线性规划问题进行求解,并采用了序列二次规划算法(sequential quadratic programming,SQP)求解非线性规划问题.最后,通过仿真实例对制导策略进行校验,以及与Lambert双脉冲直接转移制导策略进行对比,验证了本文远程导引策略的有效性和优越性.
1 问题描述与模型
月面起飞快速交会远程导引过程如图1所示.
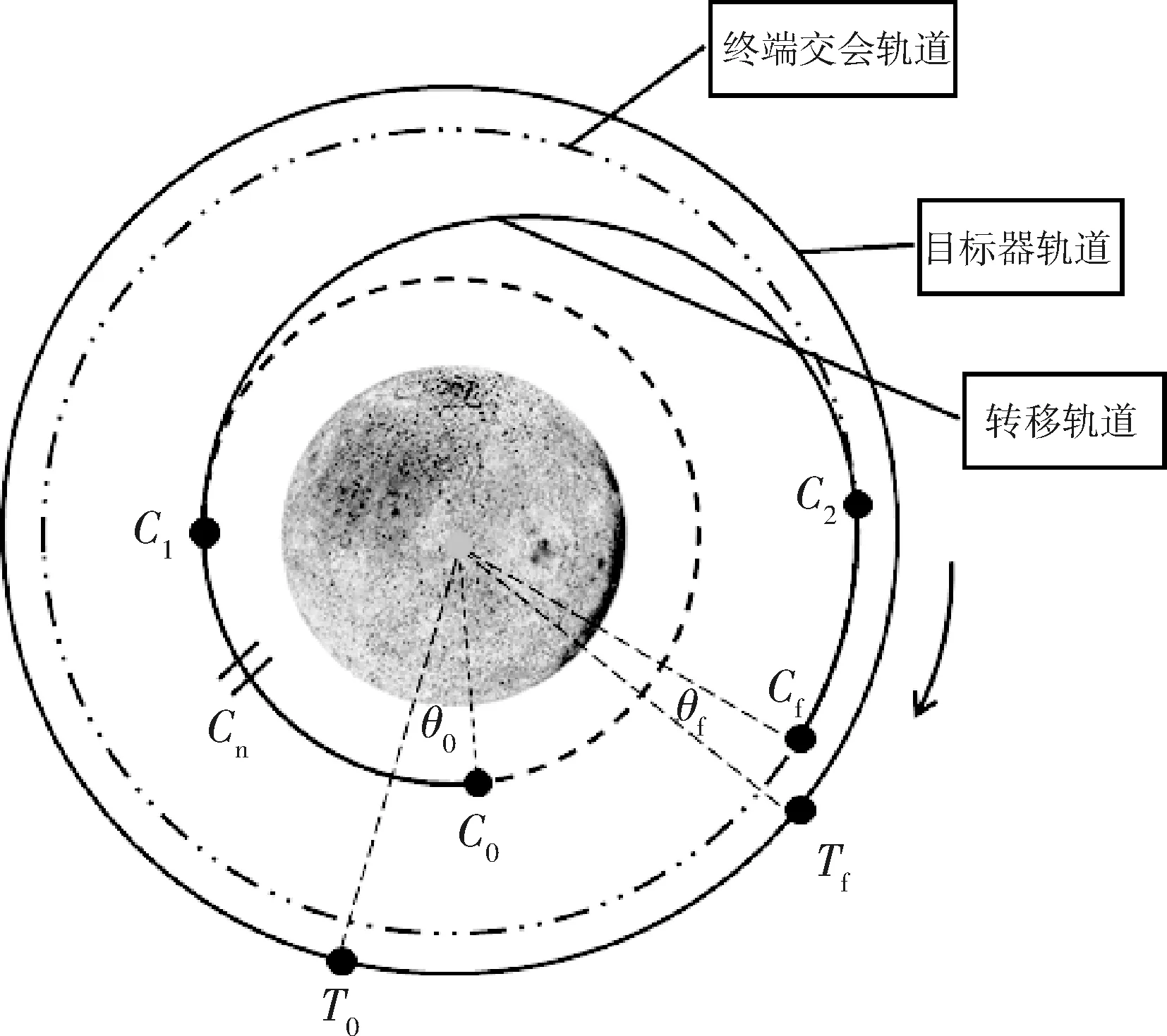
图1 月面起飞快速交会远程导引示意图
目标器入轨后(C0点)位于环月近圆轨道,此时与目标器(T0点)之间的初始相位差为θ0,经过Cn处轨道面调整脉冲,C1和C2处的双脉冲制导,追踪器在指定的时间内到达远程导引的终点(Cf点),终点处追踪器与目标器(Tf点)之间的相位差为θf,此时追踪器的轨道是略低于目标器轨道的环月圆轨道.
高斯摄动方程是用来描述轨道六要素和加速度之间的微分方程,它可以较为方便描述控制矢量f对轨道要素的影响.在卫星轨道坐标系(RTN)中,原点o位于航天器质心,r轴沿着月心指向航天器的方向,t轴沿航天器运动方向,且与t轴垂直,n轴沿着其和r轴、t轴构成右手正交坐标系的方向.控制矢量f在此坐标系下可以分解为[frftfn],其中,fr称为径向分量,fn称为法向分量,ft称为周向分量.由于近圆轨道的偏心率较小,通常使用基于非奇异轨道要素描述的高斯摄动方程,即
(1)
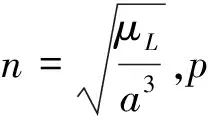
(2)
式中,(ΔvrΔvtΔvn)是速度增量Δv在RTN坐标系下的分量.由于是近圆轨道,轨道的偏心率e较小,可以近似为零,根据式(2)可以得到:
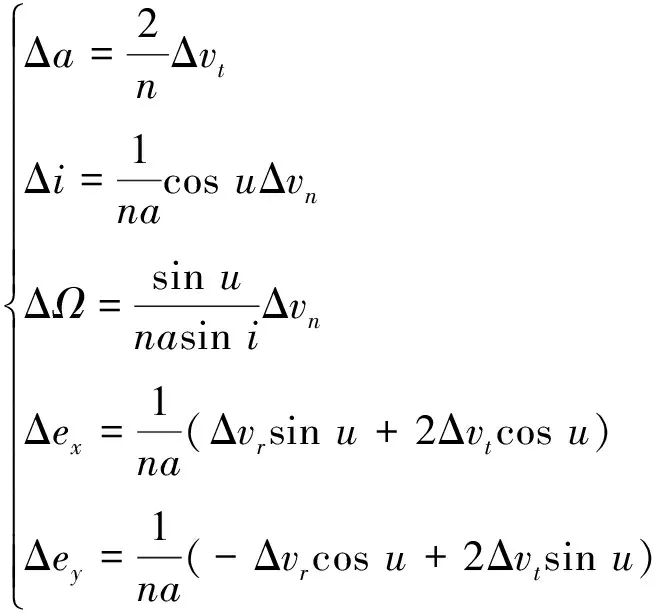
(3)
由式(3)可以看出,轨道倾角、升交点赤径即轨道面外的修正只与法向分量有关,半长轴、偏心率和近月点幅角即轨道面内的修正只和径向分量和周向分量有关,因此,面内和面外轨道要素的修正可以分开来进行考虑.
2 远程导引制导律设计
2.1 平面外轨道要素的调整
轨道平面外轨道要素的调整既可以通过两次法向脉冲对轨道倾角和升交点赤径分开来进行修正,也可以通过一次法向脉冲对轨道倾角和升交点赤径进行联合修正[17]65.
(1)分开修正
从燃料消耗最优的角度考虑,对轨道倾角的修正应在升交点(un=0)或者降交点(un=π)的位置进行,所需要的法向速度增量为
Δvn=±naΔi
(4)
Δvn=±naΔΩsini0
(5)
式中,i0是追踪器初始的轨道倾角.
(2)联合修正
联合修正是在轨道适当的位置施加一次法向脉冲同时完成轨道倾角和升交点赤径的调整,与分开修正的方法相比,联合修正的方法能够减少燃料消耗,本文采用联合修正的方法对追踪器平面外的轨道要素进行修正.根据式(3)的第二和第三个等式可以得出,联合修正所需要的法向速度增量为
(6)
联合修正的位置为:

(7)
2.2 平面内轨道要素的调整
在一般的轨道控制中,通常只关心半长轴、偏心率和近月点幅角三个平面内轨道要素的变化,体现在Δa、Δex和Δey中.在远程导引任务中,由于目标器的近月点幅角不固定,采用单脉冲完成半长轴、偏心率和近月点幅角的调整会对脉冲施加时刻有严格的要求,有时会需要较大的速度增量,难以满足节省燃料的要求,本文使用双脉冲实现对追踪器轨道的控制.根据式(3)可以得到
(8)
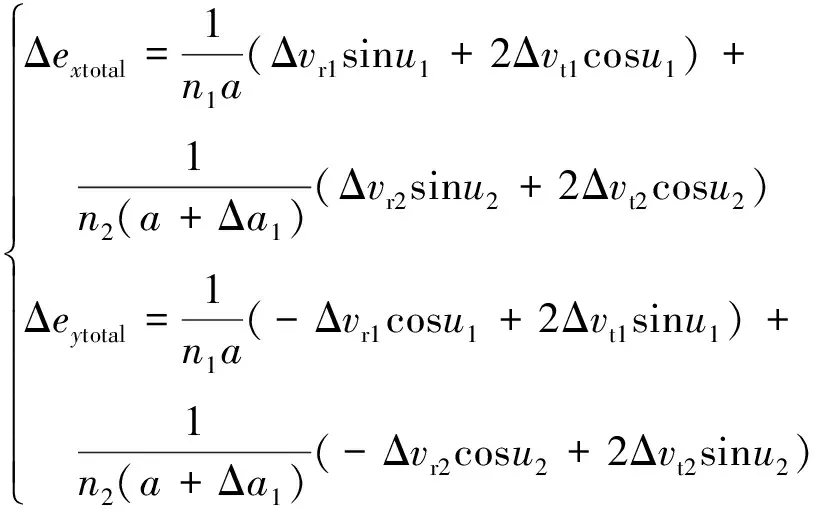
(9)
式中,Δa1、Δa2分别是第一次脉冲和第二次脉冲施加后轨道半长轴的改变量,n1、n2分别为初始轨道和第一次脉冲施加后轨道的平均角速度,u1、u2分别为第一次和第二次脉冲的施加位置.把式(8)中的Δvt1、Δvt2代入到式(9)中,可以得到
(10)
为了方便表示,式(10)中等式右边分别用F1(Δa1,Δvr1,Δvr2,u1,u2)和F2(Δa1,Δvr1,Δvr2,u1,u2)来表示.通过计算出式(10)的两次速度增量,就可以完成追踪器在远程导引过程中平面内轨道要素的调整.
2.3 双脉冲制导非线性规划
在快速交会远程导引任务设计中,不仅需要完成对追踪器轨道的调整,还需要考虑远程导引时间的约束.设追踪器初始轨道半长轴为ac,远程导引时间为ttotal.本文基于Kepler第三定律[21]设计了追踪器远程导引过程中所需要满足的时间约束方程.追踪器的轨道平均角速度和其转过的角度之间的关系为
(11)
式中,Δθi是追踪器在每段漂移轨道转过的角度,Δti是追踪器在每段漂移轨道的漂移时间,nci为追踪器在每段漂移轨道的平均角速度,计算公式为
(12)
式中,aci是追踪器在每一段漂移轨道的半长轴.如果把Δti近似地用追踪器转过的角度来表示,就可以得到
(13)
式中,Δui为追踪器在每段漂移轨道转过的纬度幅角.式(13)就是追踪器在远程导引过程中需要满足的时间约束.
综合式(10)~式(13),可以得到基于高斯摄动方程的双脉冲制导策略需要满足的制导方程
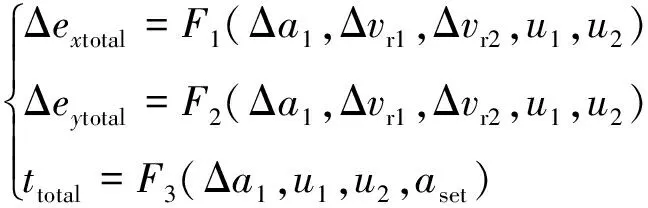
(14)
式中,F3(Δa1,u1,u2,aset)是关于Δa1,u1,u2的时间函数,aset是追踪器远程导引终点处的轨道半长轴.
根据式(14)可以看出,此非线性方程组中有5个变量,3个方程,理论上有无穷多解.为了获得满足此非线性方程组约束的燃料消耗最优解,需要对其中的变量进行规划,即
(15)
式中,P(Δa1,Δvr1,Δvr2,u1,u2)=0是式(14)的非线性方程组的约束.本文使用SQP算法对此非线性规划问题的求解.SQP算法是一种基于可行方向搜索的约束最优化方法,它具备整体收敛性的同时保持局部超一次收敛性,是轨迹优化设计中一种应用非常成功的算法,MATLAB的优化工具箱中包含了SQP算法,本文利用MATLAB的fmincon函数对此问题进行求解.
2.4 双脉冲制导的迭代优化
在式(14)的推导过程中,由于对一些变量的忽略以及近似计算,基于高斯摄动方程的双脉冲制导策略会有一定的制导误差,为了减少制导误差,本文提出了一种在二体轨道动力学模型下进行修正的迭代算法,迭代优化的过程如下:
2)利用SQP算法求解双脉冲制导非线性规划问题,获得初始解.
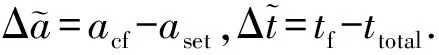
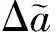
双脉冲制导迭代优化的流程图如图2所示.
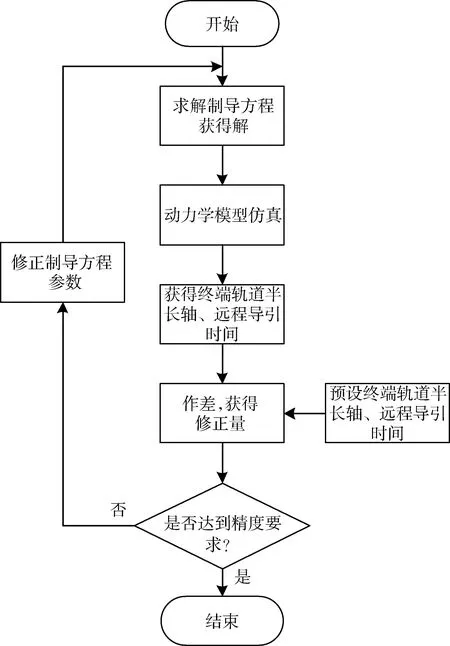
图2 迭代优化流程图
3 仿真校验
初始时刻目标器和追踪器的轨道参数如表1所示.
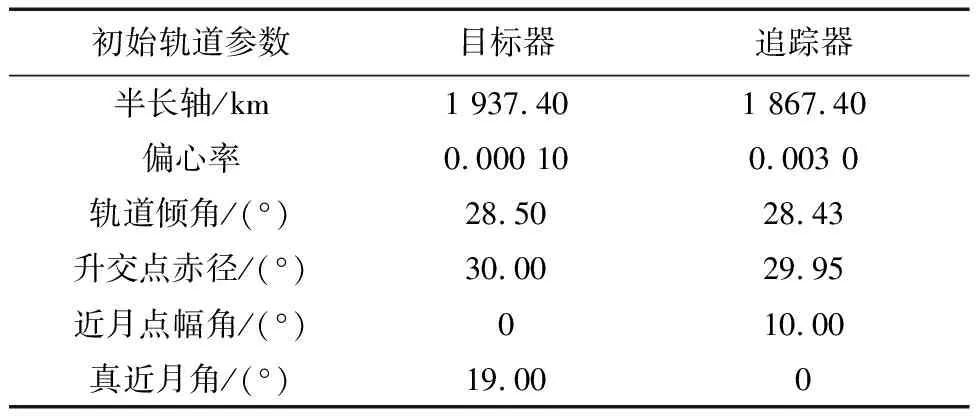
表1 航天器初始轨道参数
根据以上航天器初始轨道参数,利用本文设计的基于高斯摄动方程的双脉冲制导策略在月球轨道上进行仿真,轨道的摄动考虑月球的非球形引力摄动以及地球的引力摄动,远程导引时间设定为5 000 s.RVD坐标系中,原点o位于目标器的质心,oz轴沿着目标器指向月心的方向,oy轴沿着目标器轨道角动量方向,ox轴沿着其和oy轴、oz轴构成右手正交坐标系的方向.在此坐标系下,追踪器初始位置为[292.66 0.37 98.56](km),追踪器远程导引终点的位置设计为[8 0 3.5](km).可以求出,在远程导引段的终点,追踪器的终端轨道半长轴为1 933.9 km,目标器领先追踪器的相位大约为0.24°.
为了验证迭代优化的方法对制导误差的改善作用,不考虑轨道摄动,在远程导引终点处,得到追踪器在RVD系下轨道面内的相对位置随着迭代次数的变化如图4所示.
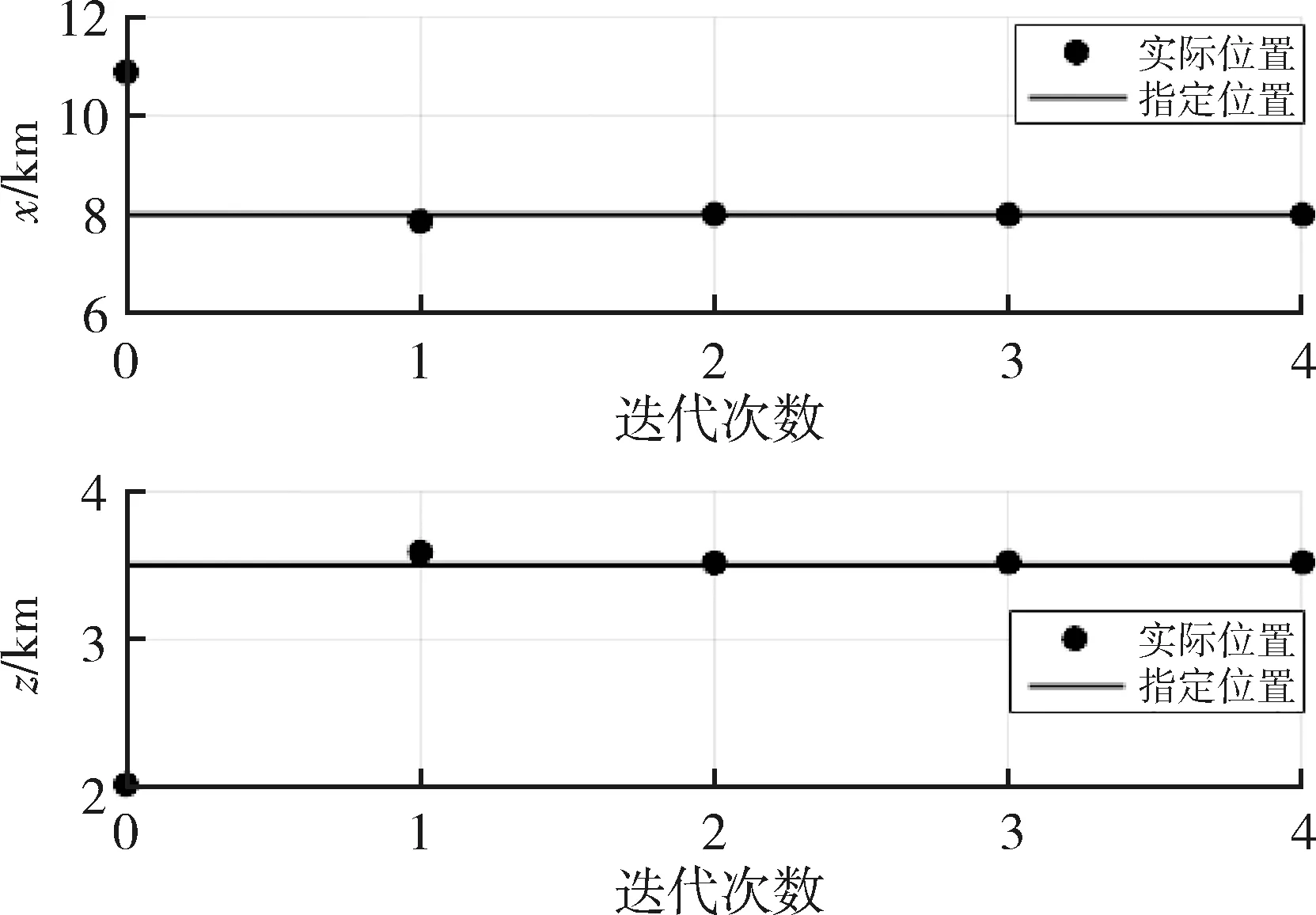
图4 追踪器终点位置随着迭代次数的变化
从图4可以看出,通过4次迭代,追踪器的终点位置就由初始的[10.87 2.02]km优化到了指定的位置.
考虑月球轨道摄动,在精确轨道动力学模型下进行仿真,得到追踪器在RVD系下相对于目标器的运动轨迹为
图5中,Δvn表示轨道面外修正脉冲,Δv1表示双脉冲制导的第一次脉冲,Δv2表示双脉冲制导的第二次脉冲.通过图5(b)可以看出,追踪器施加Δvn后,轨道面外的相对位置基本上接近0.追踪器的轨道要素随着时间的变化如图6所示.
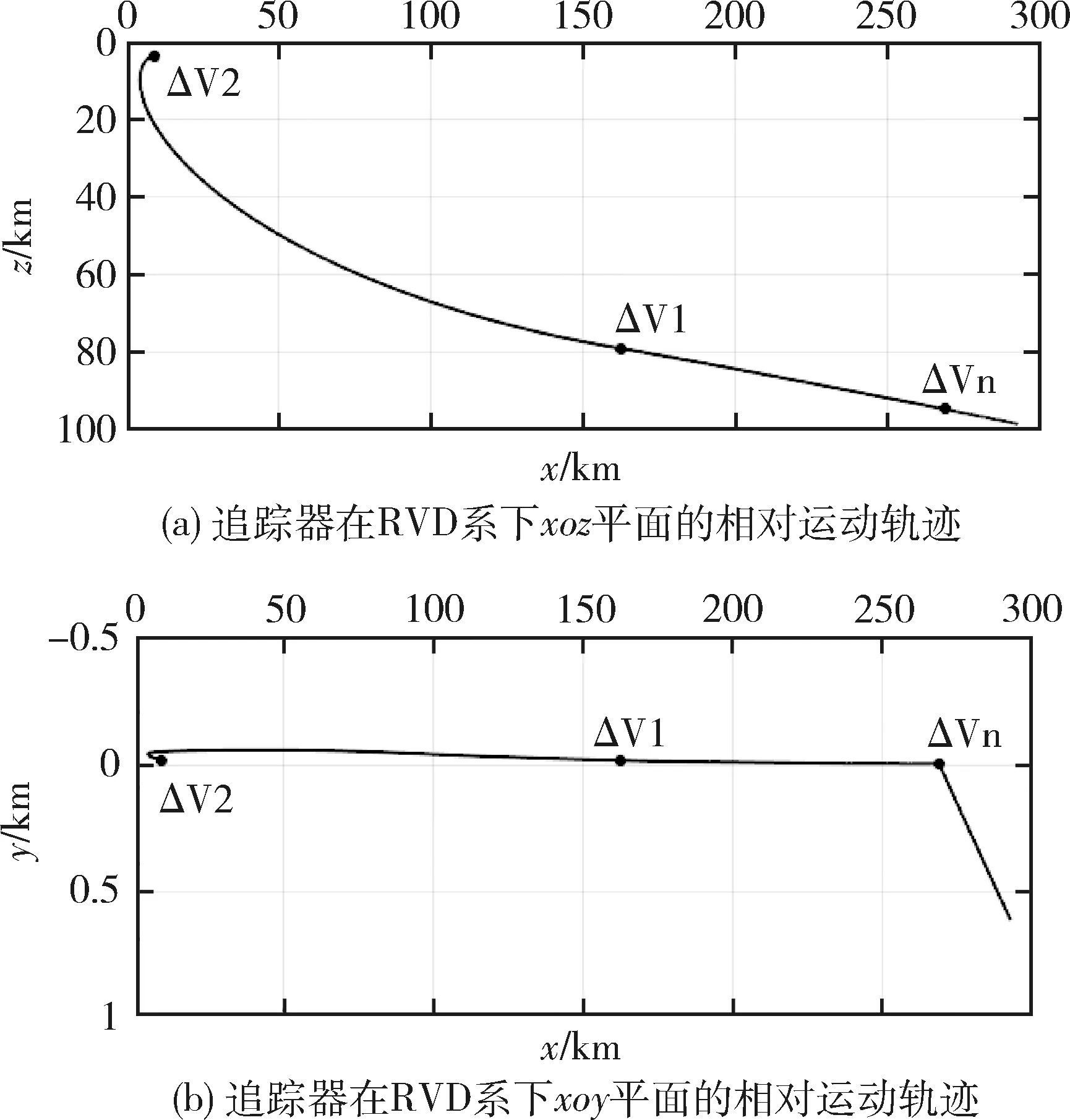
图5 追踪器在RVD系下的相对运动轨迹图
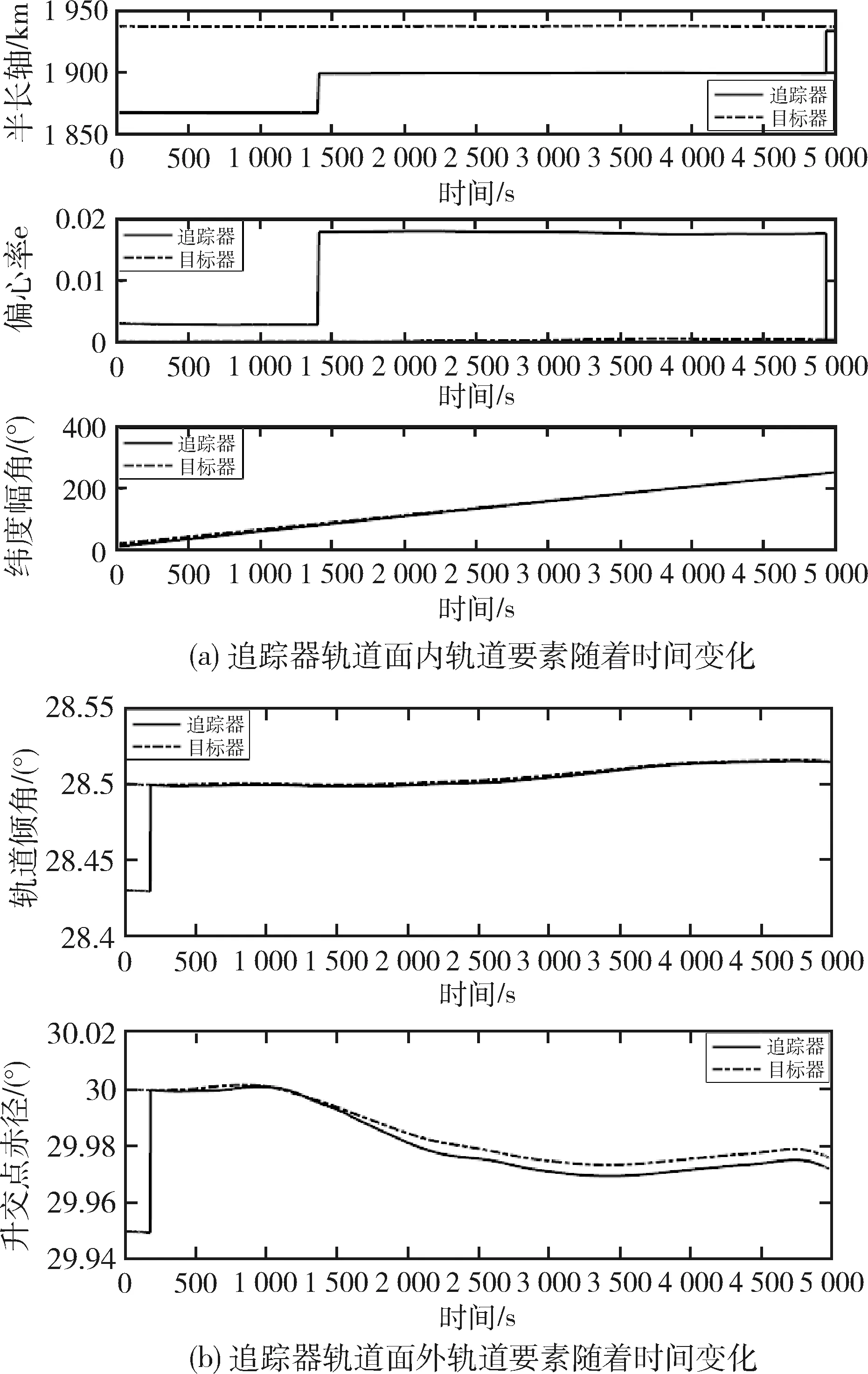
图6 追踪器的轨道要素随着时间的变化图
在远程导引终点时刻,得到追踪器和目标器的轨道参数如表2所示.
经过仿真,在远程导引终点时刻得到追踪器在RVD系下的位置为:[8.08 6.4×10-43.66](km),考虑到轨道摄动以及制导误差的影响,综合图6和表2中的数据,可以认为追踪器的终点满足远程导引终点精度的要求.
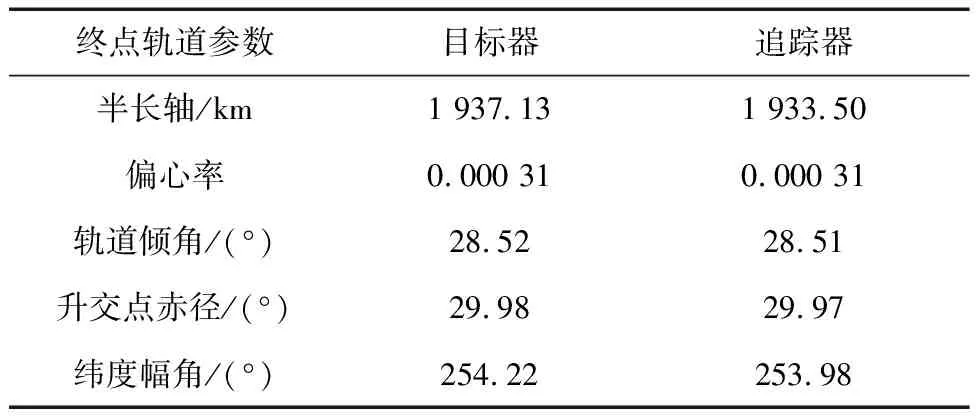
表2 航天器终点轨道参数
为校验通过把非线性方程组的求解问题转化为求解非线性规划的问题达到了优化燃料消耗的目的,采用最小二乘算法对式(14)直接求解,由于式(14)理论上有多解,解的结果与给定的初始值有关,给定与SQP算法求解非线性规划问题的相同的初始值,获得在目标器领先追踪器不同初始相位下制导所需的速度增量与使用SQP求解非线性规划问题制导所需要的速度增量对比图如图7所示.
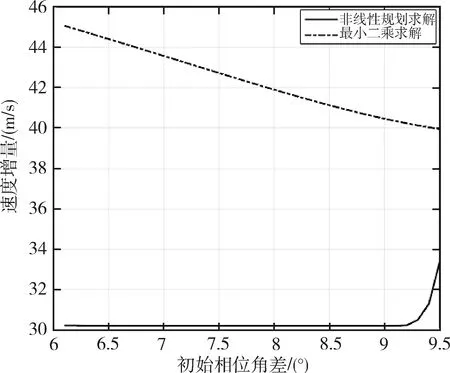
图7 不同初始相位下的所需速度增量对比图
通过图7中速度增量的对比曲线,可以看出采用SQP方法求解非线性规划问题,实现了对燃料消耗优化的目的.
采用表1中的初始轨道参数,利用Lambert双脉冲直接转移制导策略[22-23]实现追踪器由初始位置到终点位置的转移,在二体轨道动力学模型中以及精确轨道动力学模型中获得追踪器在RVD系下相对于目标器的运动轨迹为:
由于Lambert双脉冲制导属于综合变轨,每次变轨脉冲包含轨道面内和轨道面外的分量,因此不需要额外的轨道外的修正脉冲.通过图8(b)可以看出,追踪器经过双脉冲远程导引后,轨道面外的相对位置也基本上接近0.不过通过图8可以看出,在二体轨道动力学模型下,通过Lambert双脉冲直接转移,追踪器可以精确地到达指定的位置,但是在有摄动的情况下,追踪器实际终点位置与理论位置相比,存在一定的误差.通过仿真,得到在RVD系下,追踪器通过基于高斯摄动方程的制导策略以及Lambert直接转移策略的实际终点位置和理论终点位置的对比表如表3所示.
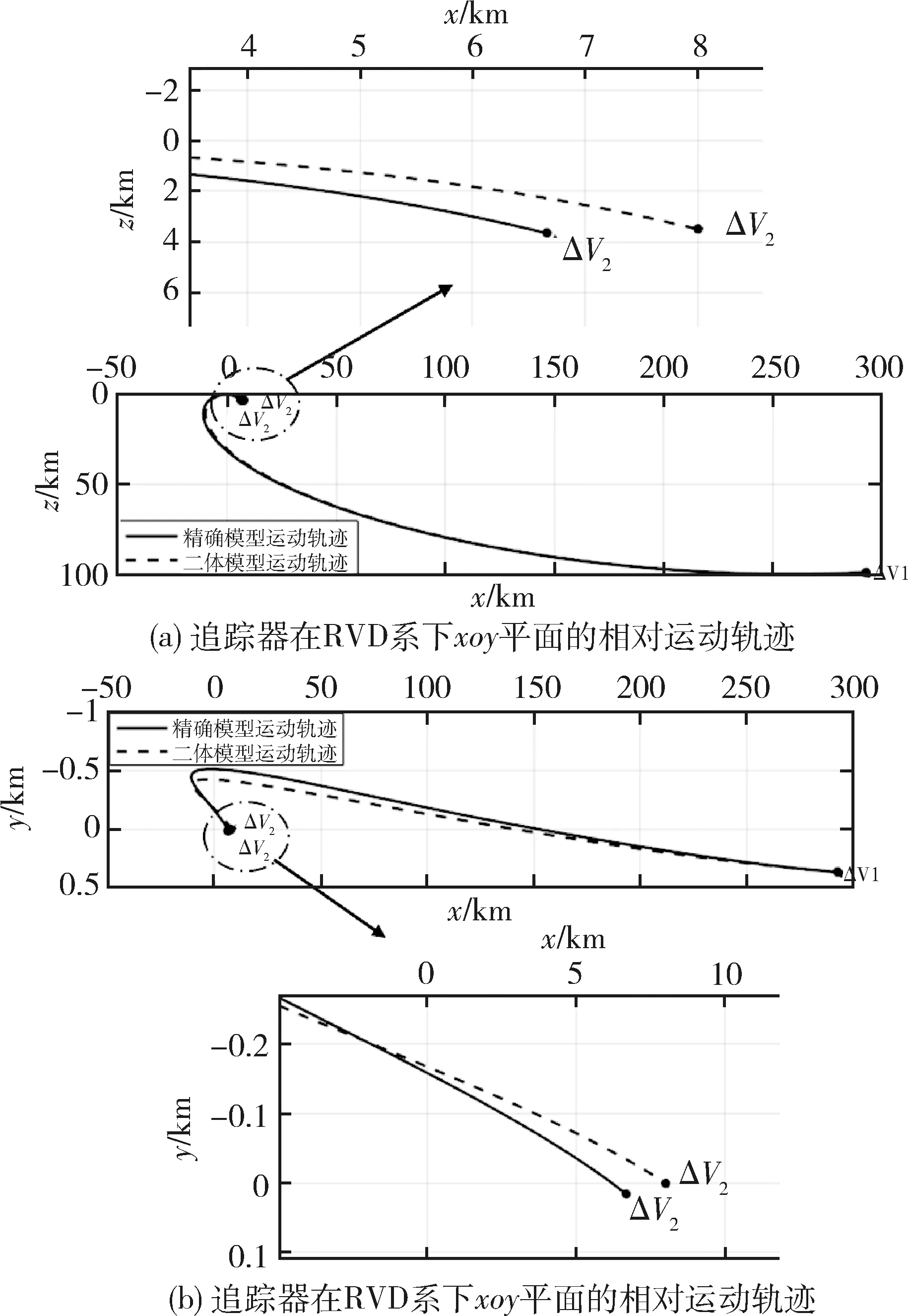
图8 追踪器在RVD系下的相对运动轨迹图
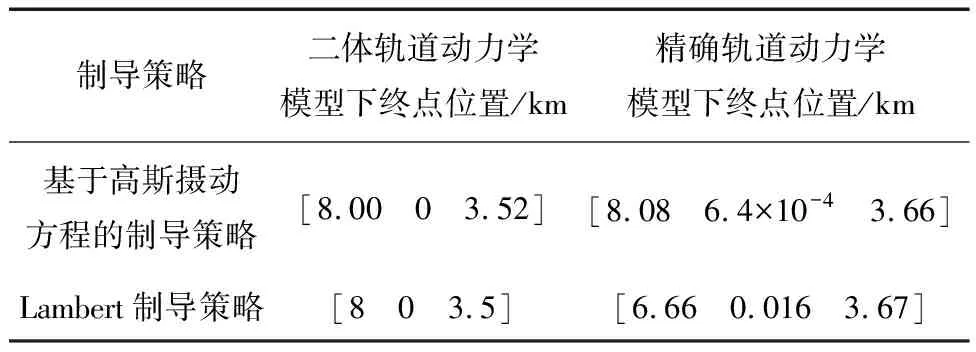
表3 RVD系下追踪器终点位置对比
通过表3中的数据对比,可以发现Lambert双脉冲直接转移的方法得到的实际结果精度较低,这是因为Lambert制导的方法是基于二体动力学进行设计的,轨道摄动对实际制导结果的影响较大.本文设计的基于高斯摄动方程制导的方法采用轨道要素进行分析,轨道摄动对追踪器轨道和目标器轨道的影响效果基本上是一致的,整体来看所求的结果受摄动的影响较小.进一步,统计两种方法在远程导引过程中所需要速度增量的情况如表4所示.

表4 远程导引所需要速度增量对比
通过表4中的对比数据可以看出,基于高斯摄动方程制导方法所需要的速度增量较少,达到了优化燃料消耗的目的.
在5 000 s的远程导引时间下,通过改变目标器领先追踪器不同初始相位角,分别利用基于高斯摄动方程的制导策略和Lambert双脉冲直接转移的制导策略进行打靶仿真,在远程导引终点,获得追踪器在RVD系下实际的相对位置如图9所示.
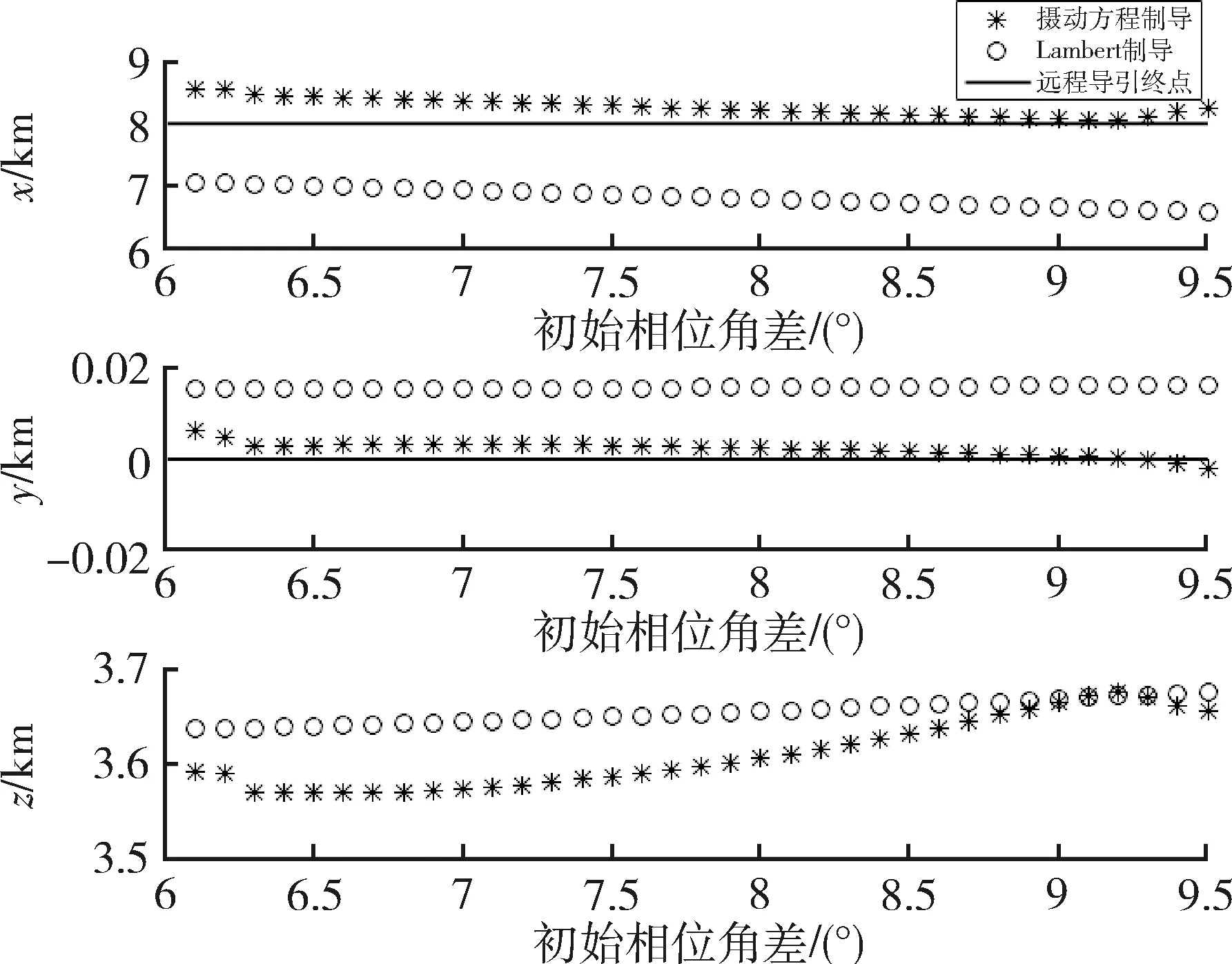
图9 不同初始相位下追踪器终点位置对比
从图9可以看出,在不同初始相位下,采用高斯摄动方程制导方法的制导精度都要高于Lambert直接转移制导方法的制导精度.进一步,比较两种方法所需要总的速度增量,如图10所示.
从图10可以看出,相比于Lambert直接转移制导方法,采用高斯摄动方程制导方法所需要的速度增量得到了优化.在初始相位角差6.10°~9.30°的区间,高斯摄动方程制导方法所需的速度增量的变化幅度非常小,均为30.22 m/s左右.
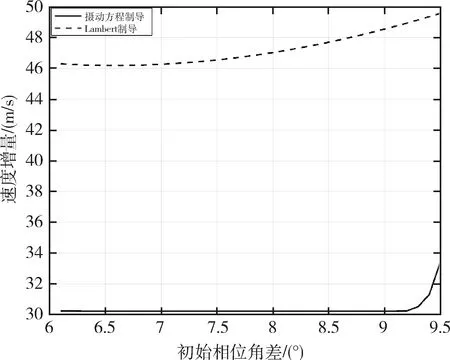
图10 不同初始相位下所需速度增量对比
考虑到制导时间对Lambert制导所需要的速度增量的影响,使用表1中目标器领先追踪器的初始相位,通过改变远程导引的时间,对基于高斯摄动方程的制导策略和Lambert直接转移的制导策略需要总的速度增量进行比较,如图11所示.
通过图11可以看出,本文设计的基于高斯摄动方程的制导策略在不同的制导时间下所需要总的速度增量基本上是相同的,均为 30.22 m/s左右,而且相比于Lambert直接转移的制导策略,完成远程导引任务需要的速度增量均得到了优化,进一步表明本文设计的制导策略在燃料消耗方面的优越性.
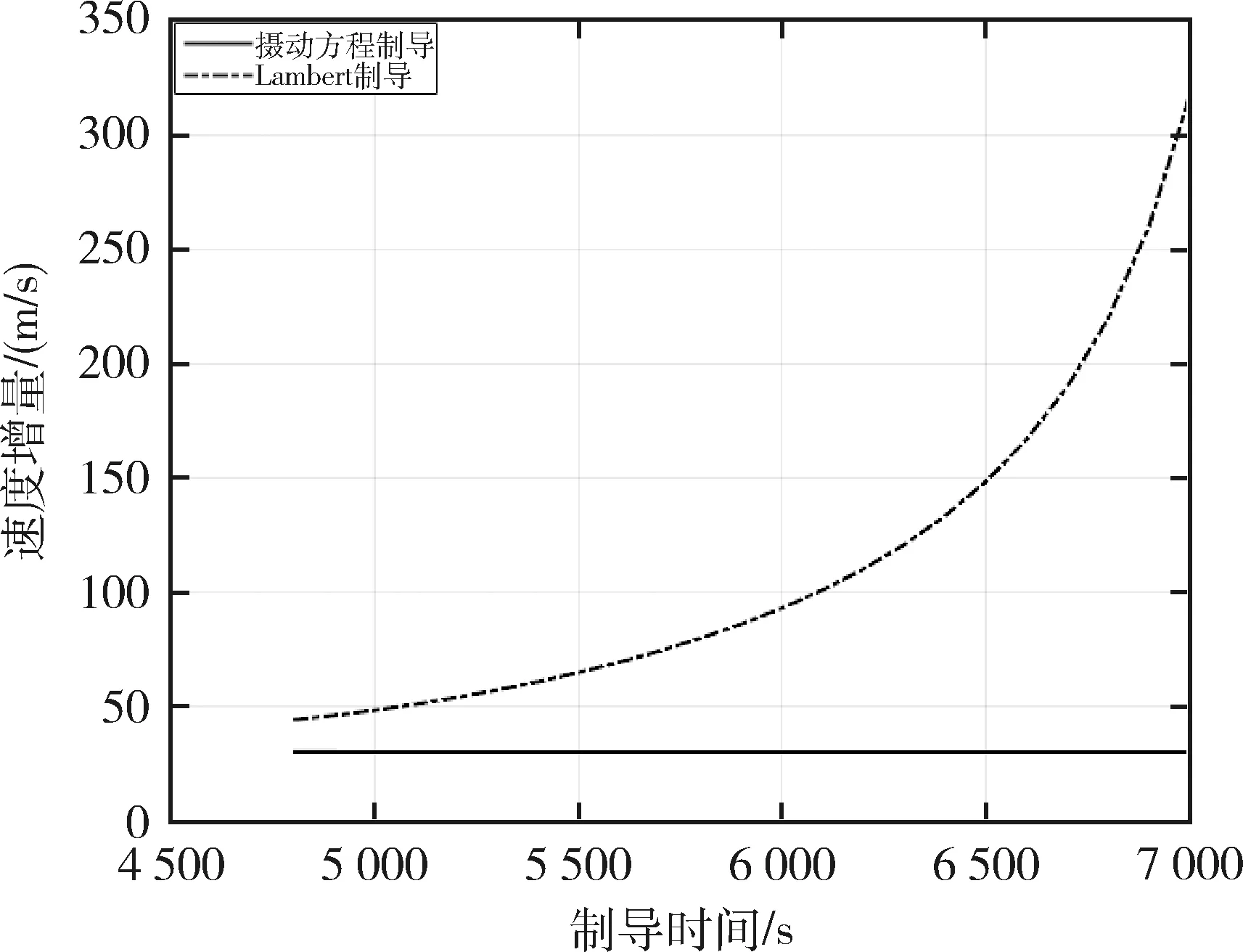
图11 不同制导时间下所需速度增量对比
4 结 论
对于月面起飞快速交会远程导引的问题,本文基于高斯摄动方程设计了一种双脉冲制导律,按照这种方法在月球轨道对追踪器进行快速交会远程导引,制导的终点精度高,所需燃料消耗得到了优化.通过仿真实例对本文设计的制导律的正确性进行校验,并与Lambert双脉冲直接转移的制导律进行对比,验证了本文设计的制导律的正确性和有效性.

