考虑踏面制动热应力的不同磨耗弹性车轮强度校核*
刘 智 陈 刚 朱逸伦 黄孝卿 周 信
(1.宝武集团马钢轨交材料科技有限公司 安徽马鞍山 243000;2.上海工程技术大学城市轨道交通学院 上海 201620)
弹性车轮具有良好的减振降噪性能,已广泛应用于有轨电车,并且在地铁减振降噪方面也具有潜在优势[1-2]。目前绝大多数低地板有轨电车的走行系统均使用了具有减振降噪效果的弹性车轮[3],为防止弹性车轮在各种复杂运营工况下出现材料疲劳损伤和破坏,在设计阶段对车轮进行静强度与疲劳强度计算分析与校核至关重要[4]。
在城市轨道交通车辆运行过程中,由于站间距短、行车密度高等因素造成车辆频繁的启动和制动。踏面制动是城市轨道列车和地铁车辆的基本制动方式,制动系统在制动过程中由于摩擦产生的热量,将会导致金属部件和橡胶件的工作温度急剧升高,引起车轮产生较大的热载荷,同时车轮还承受来自车辆的全部载荷,热载荷和结构载荷剧烈的共同作用往往造成车轮的疲劳损伤,对车轮的寿命造成一定的影响。
近年来对车轮制动热应力的研究,国内外学者做出了较多的研究。HAIDARI和TEHRANI[5]对运行中出现裂纹的车轮进行热力耦合分析,热载荷对车轮疲劳寿命的影响不可忽略。李金良等[6]对比分析了车轮在制动过程中及制动结束后辐板位置的残余应力和热应力。LONSDALE[7]对比了不同闸瓦位置制动对车轮温度场的影响。张琪等人[8]建立了不同地铁车轮结构几何参数下的踏面模型,计算了不同模型下制动热负荷的变化情况。曹茹和商跃进[9]建立了踏面制动的热-结构耦合瞬态非轴对称三维有限元模型,对热疲劳问题进行分析,得出拖曳制动工况危险点位于辐板处的结论。以上研究多是针对刚性车轮进行制动热分析,对于弹性车轮的制动热和应力分析还较少。因此有必要分析制动过程产生的热量对弹性车轮的影响。
本文作者针对采用踏面制动的地铁弹性车轮进行强度校核,考虑了结构场和温度场的相互影响,对不同磨耗下的车轮进行研究,为弹性车轮在地铁列车上的运用提供了理论依据,也为今后地铁弹性车轮的设计提供一定参考。
1 弹性车轮有限元模型
1.1 模型参数
为探究踏面制动热对弹性车轮应力分布的影响,以某地铁弹性车轮为例,建立了弹性车轮实体有限元模型,如图1所示,弹性车轮主要由轮辋、轮芯、安装环和橡胶层组成。安装环与轮芯之间通过16根紧固螺钉连接,橡胶与轮辋之间均采用过盈配合。计算模型分为新轮和磨耗车轮。其中新轮为新出厂车轮,直径为840 mm,后文中统称为新轮;磨耗车轮为磨耗到极限的车轮,直径为770 mm,后文中统称为磨耗轮。

图1 弹性车轮有限元模型
模型采用八节点六面体导热单元进行网格划分,忽略了不影响计算结果的注油小孔以及结构倒角等。进行3次紧急制动温度场分析后,将导热单元转换成八节点六面体结构单元,将热计算的温度场作为荷载加载在模型上,进行结构分析。模型在车轮的轴端面进行约束,螺栓与螺栓孔间采用绑定接触,其余各个部件之间均采用摩擦接触,弹性车轮金属部分采用ER9淬火钢材,黏弹性橡胶块采用天然橡胶材料,主要组成部件材料参数如表1所示。

表1 车轮模型计算参数
1.2 模型验证
采用1∶1制动动力试验台对车轮表面瞬时温度进行测试,如图2所示。在一次完整紧急制动过程中,实验与仿真踏面最高温度-时间历程曲线对比如图3所示。可以看出,实验过程中一次紧急制动温度上升141.1 ℃,仿真过程中一次紧急制动温度上升142.3 ℃。由于制动试验台相对大地为静止转动,其对流换热较小,故紧急制动后温度下降较慢。实验与仿真温度随时间总体变化规律相符,且幅值大小相近,说明仿真结果具有合理性,可以反映真实制动过程中车轮的温度变化规律。

图3 实验和仿真踏面温度对比
2 计算工况
2.1 力学应力计算工况
参考UIC510-5[10]和EN13979-1[11]标准进行载荷的施加,包括直线、曲线和道岔工况,加载的位置如图4所示。其中直线工况加载Fz1,曲线工况同时加载Fz2和Fy2,道岔工况同时加载Fz3和Fy3。各计算工况荷载值如表2所示,表中m为轴质量的1/2。

图4 横弹性车轮踏面加载位置示意

表2 车轮模型相关计算参数
2.2 制动热计算工况
为校核极限状态下弹性车轮制动温度应力情况,文中计算车辆连续3次踏面紧急制动:以80 km/h初始速度进行100%踏面制动,制动结束后停留11 s,加速到初始速度后开始下一次紧急制动,如此循环3次,第3次制动后列车停止。采用最高温度时刻对车轮静强度和疲劳强度进行校核,车辆运行速度-时间历程曲线如图5所示。

图5 车辆运行速度-时间历程
2.3 制动热边界条件
踏面制动时车轮温度的大小主要由2个因素决定,第一是摩擦传给车轮的热量,第二个是车轮对空气的对流换热。
制动过程中,车轮与闸瓦接触热流输入的边界条件采用导热问题第二类边界条件,除轴孔边界以外的车轮其他表面,全部为导热问题第三类边界条件,如图6(a)所示。踏面制动热热流密度的加载主要有旋转热源法和均布热源法2种方法,对于较厚轮辋2种计算方法得到的温度场差异较小[12],故文中采用均布热源法进行加载,即认为闸瓦与车轮踏面间摩擦产生的热量是瞬时均布加载在车轮踏面一周。
在加速和停留过程中,除轴孔以外的车轮所有表面为导热问题第三类边界条件,如图6(b)所示。

图6 踏面温度达到峰值时应力云图
采用能量换算法计算第二类边界条件踏面热流密度。制动过程中列车损失的能量Q(t)为
(1)
其中,
v(t)=v0-abt
(2)
式中:m为轴质量的1/2;v(t)为车辆瞬时速度;v0为制动初速度;ab为制动减速度;t为制动时间。
在制动过程中,由于存在轮轨摩擦和空气阻力等因素,制动时产生的动能只能有一部分转化为热能,而转化的热能只有部分被车轮吸收,其余部分被闸瓦吸收,部分热量通过空气热传导。车轮与钢轨接触的导热等情况并没有完全将热量输入至车轮,踏面的热流输入必须考虑在车轮和闸瓦之间的分配问题。取η为热流分配系数,表示热量传递到车轮的比例。采用均布热源法,将计算所得热量通过热流密度q(t)均布加载在车轮踏面上,热流密度为单位时间、单位面积下的热量分布值,其计算公式为
(3)
式中:q(t)为热流密度;η为热流分配系数;S为踏面摩擦环带面积。
热流分配系数η为
(4)
式中:λw、λb、∂w和∂b分别为车轮和闸瓦的导热系数和导温系数。
根据合成闸瓦特点,取热流分配系数η=0.91[13]。
目前,对流换热系数的确定方法主要有公式推导法、经验公式法和CFD流体软件仿真计算法。根据以往研究经验[14],文中计算对流换热系数采用经验公式法,因此第三类边界条件表面换热系数表示为
h(t)=0.382 8+14.39v(t)
(5)
3 弹性车轮热力耦合分析
3.1 弹性车轮温度及热应力
列车以80 km/h初始速度连续三次紧急踏面制动弹性车轮的温度分布,新轮和磨耗车轮踏面最高温度位置的温度-时间历程曲线如图7和图8所示。新轮和磨耗车轮最高温度均出现在第3次制动过程中。计算中使用3次紧急制动过程中踏面温度最高时刻应力对轮辋进行强度校核。

图7 新轮轮辋最高温度位置温度-时间历程

图8 磨耗轮轮辋最高温度位置温度-时间历程
采用间接耦合法对弹性车轮进行热力耦合分析,3次紧急制动过程中,踏面温度最高时刻温度云图如图9所示。新轮踏面最高温度为238 ℃,磨耗轮踏面最高温度为259 ℃;由于橡胶的隔热作用,3次踏面紧急制动过程中,轮芯和安装环部分温度上升较小,均不到0.1 ℃。

图9 踏面温度达到峰值时温度场云图(℃)
踏面温度最高时刻新轮和磨耗轮3次紧急制动过程中轮辋温度最高时刻热应力云图如图10所示。可以看出热应力的影响主要在轮辋部分,轮芯和安装环由于温度几乎没有上升,应力变化很小。轮辋部分应力主要存在于踏面部分和轮辋下表面,其中新轮踏面最大热应力为329 MPa,磨耗轮踏面最大热应力为321 MPa,而在车辆正常运行时,力学应力主要集中在弹性车轮轮辋下表面,故在静力校核和疲劳校核时应主要考虑踏面制动热对轮辋部分下表面的影响。

图10 踏面温度达到峰值时应力云图(MPa)
普通刚性车轮制动时产生的热应力主要集中在辐板,而相同结构弹性车轮的热应力主要集中于车轮轮辋,明显减少了踏面制动热应力引起的车轮辐板疲劳损伤。
3.2 热力耦合应力静强度分析
在弹性车轮有限元模型中,施加各载荷组合工况和约束条件,计算出弹性车轮在各种工况下的主应力σ1、σ2和σ3,通过下式计算得出von Mises应力σeqv:
(6)
用屈服安全系数Sp评估弹性车轮金属部件的静强度是否满足使用要求,Sp通过下式获得:
Sp=Re/σeqv
(7)
式中:Re为轮辋材料的抗拉极限。
表3给出了各个工况下轮辋(不包括施加集中力位置)仅有力学应力和热应力-力学应力共同作用最大等效应力值,对应的安全系数Sp如表4所示,可知Sp均远大于1,满足静强度要求,并有较大余量。

表4 各工况载荷下金属部件最小屈服安全系数Sp
对轮辋下侧危险节点由外至内进行编号,新轮和磨耗轮在3种工况下轮辋下侧危险节点距离车轮外侧横向方向上不同编号节点的应力值对比图分别如图11—13所示。可以看出踏面制动热对轮辋外侧应力分布影响较大,对于轮辋内侧(开进轮缘一侧)影响较小。

图11 直线工况横向节点对应von Mises应力分布

图12 曲线工况横向节点对应von Mises应力分布

图13 道岔工况横向节点对应von Mises应力分布
3.3 热力耦合应力疲劳分析
进行疲劳校核时参照UIC510-5[10]采用单轴疲劳准则,在弹性车轮有限元模型上施加弹性车辆在运行过程中经常遇到的载荷组合工况,选取弹性车轮有限元模型旋转一周各节点的主应力分布状态,通过如下步骤进行疲劳强度计算分析:求得所有运营载荷工况下表面节点的主应力值σ1、σ2和σ3的值,以及在全局坐标下的方向余弦;将节点在各个载荷工况下的方向应力(σx,σy,σz,σxy,σxz,σyz)在最大主应力σ11max方向上的投影,获得最大主应力σ11max方向上的最小值σ11min;
(8)
即可将多轴疲劳问题简化为单轴应力状态的疲劳如下式评价:
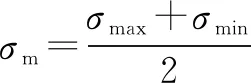
(9)

(10)
将各个节点的(σm,σa)在Goodman疲劳评价图上标出,可得到评价节点的安全系数η11。
根据轮辋疲劳强度校核计算方法,将所有运营工况下计算得到的轮辋底部表面节点的(σm,σa)值插入Goodman疲劳评价图。在计算各节点(σm,σa)时,制动热应力与力学波动应力叠加时,每次制动时产生一次高幅值应力,取其最小应力为力学应力的最小值,最大应力为热应力的最大值与力学应力的最大值的叠加[15]。图14给出了在磨耗到限条件下轮辋的Goodman曲线,图15显示了轮辋上最危险节点的位置,只有力学应力作用时轮辋下表面节点最小安全系数η11=2.7,热应力和力学应力共同作用时轮辋下表面节点最小安全系数η11=2.5。可以看出,受到踏面制动热应力的影响,轮辋外侧应力较仅考虑力学应力显著增大,故其最危险点位置从轮辋内侧节点转换到轮辋外侧节点。

图14 磨耗到限弹性车轮Goodman曲线

图15 轮辋疲劳强度最危险节点位置
4 结论
(1)80 km/h速度条件下,连续3次踏面紧急制动时,新车轮踏面最高温度为238 ℃,踏面最大热应力为329 MPa;磨耗轮轮辋会产生更高的温度,踏面最高温度为244 ℃,踏面最大热应力为321 MPa。
(2)3次踏面紧急制动过程中,踏面制动热会使轮辋外侧应力明显增大,对于轮辋内侧影响较小。轮芯和安装环部分温度上升较小,均不到0.1 ℃,应力变化很小。
(3)弹性车轮制动热对轮辋应力有明显影响,新轮轮辋在仅考虑力学应力时,在直线、曲线和道岔载荷3种工况下最大von Mises应力分别为41.9、56.1、50.6 MPa,在考虑热影响后分别为83.3、83.2、86.5 MPa,3种工况下较前者分别增大了98.9%、48.3%、70.9%;磨耗轮轮辋在仅考虑力学应力时3种工况下最大von Mises应力分别为76.9、101.0、90.6 MPa,在考虑热影响后分别为114.0、114.9、124.1 MPa,3种工况下较前者分别增大了48.2%、13.7%、36.9%。磨耗车轮应力值较大但热应力影响比例较小,均满足静强度要求。
(4)采用Goodman曲线对轮辋进行疲劳评价,考虑热应力前后安全系数分别为2.7和2.5,均满足疲劳校核要求,受到踏面制动温度应力的影响,轮辋部分最危险点位置与仅考虑力学应力时不同,从轮辋内侧变到轮辋最外侧。
(5)采用踏面制动弹性车轮,满足速度80 km/h的地铁车辆正常运行要求。踏面制动热会使轮辋应力分布产生较大变化,因此在设计地铁用弹性车轮时,不能仅仅考虑车轮的结构应力或热应力,应考虑二者的耦合作用,把耦合应力作为车轮强度的评价指标。

