供油条件对线接触热混合润滑性能的影响*

朱鹏娟 刘晓玲 何文卓 周亚林

(青岛理工大学机械与汽车工程学院 山东青岛 266520)

实际工程中，线接触是一种常见的接触形式，普遍应用于凸轮、齿轮和圆柱滚子等零部件中。在低速、重载、启动或制动等工况下，线接触副零部件常处于混合润滑状态。苛刻的工作条件使得润滑油呈非牛顿特性，且极易出现乏油现象。当处于乏油状态时，会加剧零部件的摩擦磨损，严重时甚至导致零部件失效。因此，有必要在分析混合润滑性能时考虑供油条件的影响。

混合润滑模型通常分为确定性模型与统计模型，确定性模型可以描述局部压力与粗糙峰局部变形，统计模型可以直接给出名义膜厚、承载力等参数[1]。与确定性模型相比，统计模型可以分析多种因素对混合润滑的影响且计算方法更简便、效率更高。PATIR和CHENG[2]基于统计模型提出了平均流量模型。该模型已得到了广泛的应用[3-5]。在实际工况中，机械设备因接触摩擦往往会产生大量的热，引起接触区温度升高，从而影响润滑油性质，因此有必要考虑混合润滑的热效应。GU等[6]基于热混合润滑模型，研究了涂层与织构对环/衬套连接性能的影响。CASTRO等[7]通过试验将接触出口润滑油温度作为从全膜润滑向混合润滑过渡的依据，评估混合弹流润滑线接触的热效应。周江敏等[8]结合圆柱滚子轴承，研究了表面纹理与硬度对热混合润滑的影响。上述文献都是基于充分供油条件。然而，大多数机械零部件由于工作持续时间长且处在高载的工况下，通常会出现乏油现象。

关于乏油润滑的研究，大多数是基于弹流方面[9-10]，针对混合润滑方面的文献较少。LI和MASSE[11]建立了乏油热混合润滑模型，讨论了不同表面粗糙度下入口乏油程度对闪温的影响。结合瞬态混合润滑模型与磨损模型，LIU等[12]研究了发动机启动前乏油条件对润滑性能的影响。KRUPKA等[13]利用球-盘接触副试验台，研究了在纯滚动条件下表面纹理对乏油接触的影响。上述文献无论是从理论还是从试验方面，研究工况都各不相同。不同的运行工况对材料的要求也有所不同。陶瓷材料因具有质量轻、刚度大、耐高温等优点逐渐受到人们的青睐。因此，在考虑供油条件的同时，有必要讨论接触副材料的影响。

综上所述，以往针对混合润滑的研究很少考虑乏油工况，而关于乏油润滑的研究主要基于弹流方面，针对乏油混合润滑的研究尚不多见。因此，本文作者基于平均流量模型，建立考虑供油条件的线接触非牛顿热混合润滑模型，并研究供油量、速度、接触副材料和环境黏度对混合润滑性能的影响，以期为改善凸轮、齿轮、圆柱滚子等零部件的混合润滑性能提供理论参考。

1 数学模型

对于混合润滑，接触区域内总压力p是由两部分组成的：油膜压力ph和粗糙峰压力pa，即

p=ph+pa

(1)

文中粗糙峰接触压力pa、摩擦力F与平均摩擦因数f表达式与文献[14]一致。

对于乏油润滑，为方便数值计算，将入口供油量作为控制乏油程度的参数，即等效供油油膜厚度hoil来表示：

hoil=(h1u1+h2u2)/ue

(2)

ue=(u1+u2)/2

(3)

式中：ue为卷吸速度；u1、u2分别为固体1、2表面的运动速度；h1、h2分别为固体1、2入口处附着的油层厚度。

1.1 Reynolds方程

在乏油润滑中，将部分油膜比例θ引入Reynolds方程，则基于平均流量模型推导的Reynolds方程为

(4)

各种当量符号表达式如下：

式中：θ=hf/h，hf为润滑油膜厚度；η*为非牛顿流体的等效黏度；ρ为润滑油密度；h为固体间隙；φx为压力流量因子，表达式为

φx=1-0.9e-0.56(h/σ)

(5)

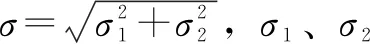
hT为两固体表面间的平均间隙，表达式为

(6)

Reynolds方程的补充条件为

ph(x)[1-θ(x)]=0

(7)

将ph(x)和θ(x)作为2个独立变量，则ph(x)>0时，θ(x)=1；ph(x)=0时，0<θ(x)<1。

式(4)的边界条件为

(8)

式中：xin、xout为计算域的边界。

1.2 黏温压方程与密温压方程

黏度η与密度ρ分别依据Roelands经验公式[15]和Dowson-Higginson公式[16]求解。

η=η0exp{A1[-1+(1+A2ph)Z0(A3T-A4)-S0]}

(9)

式中：Z0=α/(A1A2)，S0=β/(A1A3)，α、β分别为润滑油的黏压系数与黏温系数；A1=lnη0+9.67，A2=5.1×10-9Pa-1，A3=1/(T0-138)K-1，A4=138/(T0-138)；η0为环境黏度；T为油膜温度；T0为环境温度。

(10)

式中：ρ0为环境密度；εt=0.000 65 K-1。

1.3 间隙方程

两固体表面间的接触间隙方程为

(11)

式中：h00为刚体中心膜厚；R为固体1、2的综合曲率半径；E′为固体1、2的综合弹性模量。

1.4 载荷平衡方程

载荷平衡方程为

(12)

载荷比方程为

(13)

1.5 非牛顿流体有关表达式

采用Eyring流变模型，等效黏度方程为

η*=η(τ/τ0)/sinh(τ/τ0)

(14)

式中：η*为等效黏度；η表示非牛顿流体的表观黏度；τ为剪应力；τ0为特征剪应力。

1.6 能量方程

油膜能量方程为

(15)

式中：c为润滑油的比热容；k为润滑油的热传导系数；u为油膜流速；Qa为由粗糙峰引起的单位体积热量。

(16)

式中：us为粗糙峰接触时的滑动速度，us=|u1-u2|；fa为粗糙峰接触时的摩擦因数，fa=0.15。

油膜能量方程的边界条件为

T(xin，z)=T0(u≥0)

(17)

固体1、2的热传导方程为

(18)

式中：c1、c2分别为固体1、2的比热容；ρ1、ρ2分别为固体1、2的密度；k1、k2分别为固体1、2的热传导系数。

固体1、2的热传导方程边界条件：

(19)

式中：d为固体1、2变温层的深度，d=3.15bH，bH是赫兹接触区的半宽。

固体1、2表面满足如下的热流量连续条件：

(20)

2 数值方法

在数值计算中，采用多重网格法[17]求解压力，采用多重网格积分法[18]求解弹性变形，采用逐列扫描法[19]求解油膜温度。压力求解和温度场求解采用6层网格，最高层X方向的网格节点数为961，Z方向网格为22个，其中油膜内为等距网格，网格数为10；固体1、2内为不等距网格，网格数分别为6。压力的收敛精度为1×10-4，载荷的收敛精度为1×10-3，温度的收敛精度为1×10-4。压力p与部分油膜比例θ的松弛过程采用文献[20]的方法，如图1所示。

3 结果与讨论

文中数值分析输入参数有：ρ=870 kg/m3，c=2 000 J/(kg·K)，k=0.14 W/(m·K)，T0=303 K，α=2.19×10-8Pa-1，β=0.047 6 K-1，τ0=10 MPa，R=0.02 m，σ=0.4 μm，滑滚比s=0.5。接触固体参数如表1所示。

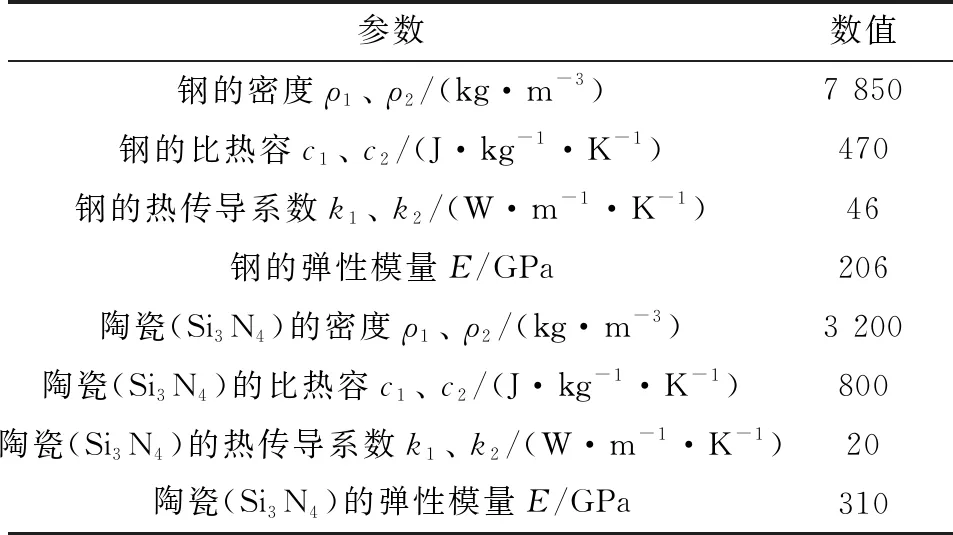
表1 接触固体参数

对于钢-钢接触，接触固体的综合弹性模量E′=226 GPa(文中3.1、3.2和3.4均基于钢-钢接触副)；对于钢-Si3N4接触，接触固体的综合弹性模量E′=269 GPa；对于Si3N4-Si3N4接触，接触固体的综合弹性模量E′=332.5 GPa。

3.1 供油量对润滑状态的影响

对于考虑粗糙度的混合润滑分析，仅依据油膜厚度来判断润滑状态是不可靠的，所以文中同时考虑膜厚比λ(λ=hmin/σ，hmin为最小膜厚)与粗糙峰接触载荷比La来判断润滑状态。图2给出了在U0=4×10-11、W0=6×10-5工况下，膜厚比与粗糙峰接触载荷比随供油量(等效供油油膜厚度hoil)的变化。可见，当供油量等于0.4 μm时，膜厚比相对较小，对应的粗糙峰接触载荷比较大，此时接触副处于边界润滑状态；当供油量大于0.4 μm且小于0.8 μm时，膜厚比随着供油量的增大迅速增大，载荷比则随着供油量的增大迅速减小，说明此时接触副处于混合润滑状态；当供油量大于等于0.8 μm时，膜厚比与载荷比变化趋于平稳，分别稳定在2.26和3.32%，此时接触副处于全膜润滑状态。

图2 膜厚比与粗糙峰接触载荷比随供油量的变化(U0=4×10-11，W0=6×10-5)

图3给出了在U0=4×10-11、W0=6×10-5工况下，最小膜厚hmin与中心膜厚hcen、平均摩擦因数f与油膜最高温度Tmax随供油量hoil的变化。可以看出，当供油量大于0.4 μm且小于0.8 μm，即乏油状态下，随着供油量的增加，最小膜厚与中心膜厚逐渐增大，摩擦因数逐渐减小，油膜最高温度逐渐增加。当供油量大于0.8 μm时，最小膜厚、中心膜厚、平均摩擦因数及油膜最高温度变化趋势减缓，最终处于一个稳定值(中心膜厚约为1.1 μm，最小膜厚约为0.9 μm，平均摩擦因数约为0.033，油膜最高温度约为85 ℃)，说明此时接触区已达到充分供油状态。

图3 最小膜厚、中心膜厚、平均摩擦因数和油膜最高温度随供油量的变化(U0=4×10-11，W0=6×10-5)

3.2 速度的影响

图4、5分别示出了在W0=6×10-5工况下，供油量分别为3.0和0.6 μm时油膜厚度、总压力、粗糙峰压力与油膜温度随速度的变化。由图4可以看出，当hoil=3.0 μm，即为充分供油条件时，随着速度的增加，油膜厚度增大，这是由于进入接触区的润滑油量随着速度的增大而增加，因此油膜厚度增加；当hoil=0.6 μm，即为乏油条件时，油膜厚度同样随着速度的增加而增大，但与充分供油相比，乏油工况下的膜厚相对较小。说明供油条件会影响油膜厚度。随着速度的增加，总压力基本没变，二次压力峰变大，说明速度对总压力影响较小。乏油条件下，二次压力峰较小，并靠近出口区，这是因为油膜厚度随供油量的降低出口颈缩变小并逐渐往出口区移动。粗糙峰压力随着速度的增加而降低，这是因为总压力由油膜压力与粗糙峰压力共同承担，总压力基本不变，油膜压力受速度影响增加，则粗糙峰压力降低。

由图5可见，随着速度的增加，油膜温度逐渐升高，且最高温升主要集中在Hertz接触区。与充分供油相比，乏油工况下的油膜最高温度相对较低，说明乏油条件会影响油膜温度。

表2给出了在W0=6×10-5时，不同速度和供油量下膜厚比λ与粗糙峰接触载荷比La。可以看出，无论是在充分供油或乏油条件下，膜厚比都随着速度的增加而增加，载荷比随着速度的增加而减小。与充分供油相比，乏油条件下的膜厚比较低，载荷比较高。这是因为乏油工况下的油膜厚度更小，粗糙峰压力更大。

表2 不同速度和供油量下的膜厚比与粗糙峰接触载荷比(W0=6×10-5)

3.3 接触副材料的影响

图6给出了在U0=4×10-11、W0=6×10-5，供油量分别为3.0和0.6 μm工况下，3种不同接触副(钢-钢、钢-Si3N4和Si3N4-Si3N4)的总压力、粗糙峰压力、油膜温度和油膜厚度分布。

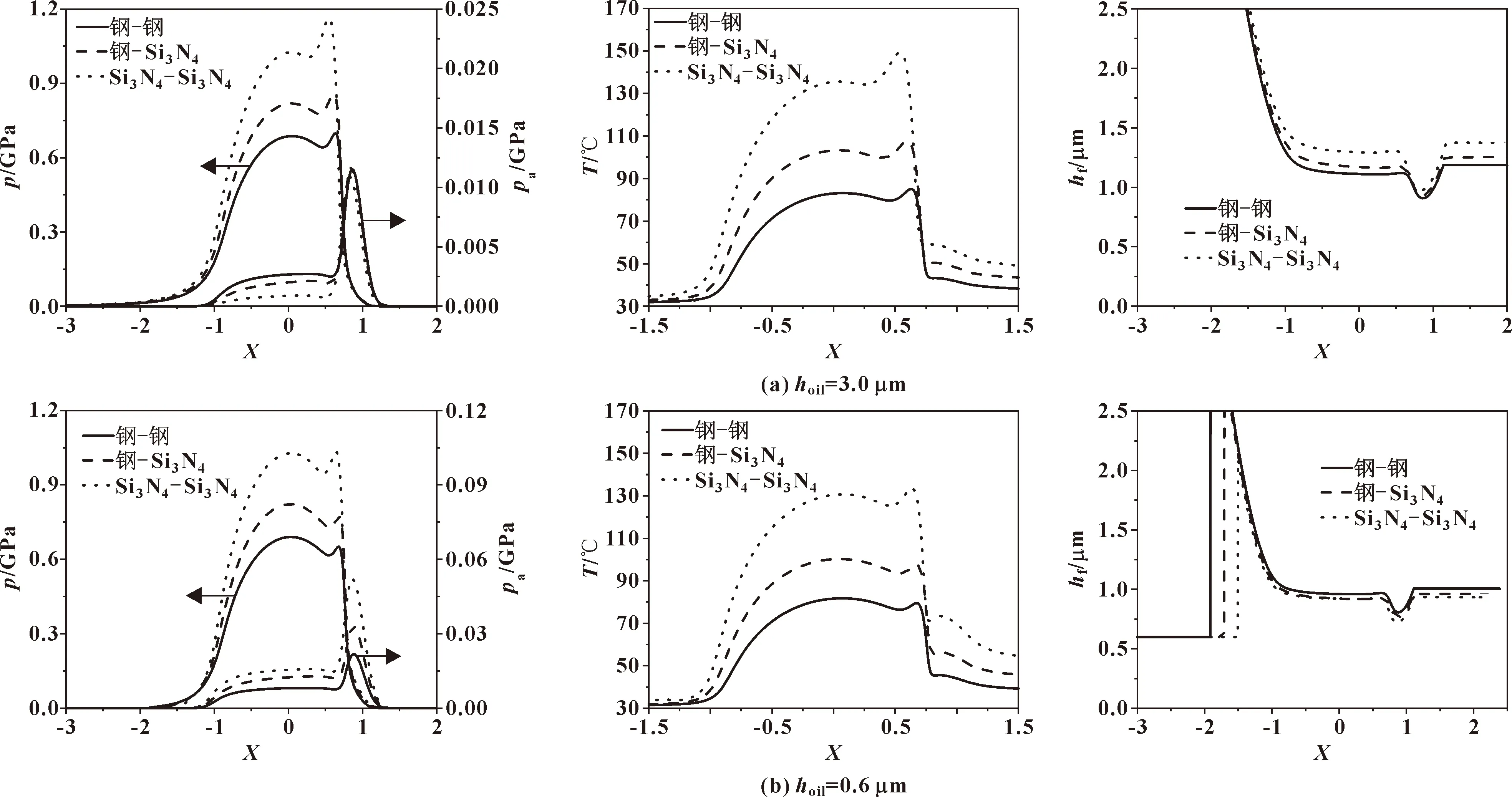
图6 不同供油条件下3种接触副的压力、油膜温度和油膜厚度(U0=4×10-11，W0=6×10-5)

由图6可见，当hoil=3.0 μm时，钢-钢接触副的总压力与油膜温度最低，Si3N4-Si3N4接触副的总压力与油膜温度最高；当hoil=0.6 μm时，3种接触副的总压力、油膜温度高低顺序与充分供油时一致。这是因为在3种不同接触副中，钢-钢接触副综合弹性模量E′最小，Si3N4-Si3N4接触副综合弹性模量E′最高。当速度参数U0和载荷参数W0一定时，E′越大，则速度ue与载荷w′越大，进入接触区的润滑油越多。因此，对应的总压力、油膜厚度越大。与钢相比，Si3N4的热传导系数更小，产生的热量更难耗散，因此，Si3N4-Si3N4接触副油膜温度更高。在充分供油条件下，Si3N4-Si3N4接触副油膜厚度较高，粗糙峰压力最低；但在乏油条件下，钢-钢接触副油膜厚度略高，粗糙峰压力最低。原因在于，乏油状态下供油量一定，Si3N4-Si3N4接触副对应的载荷w′较大且油膜温度较高，导致润滑油黏度降低，成膜能力减弱，从而使得油膜厚度变低，粗糙峰压力较大。

表3给出了在U0=4×10-11、W0=6×10-5及不同供油条件下3种不同接触副对应的膜厚比λ与粗糙峰接触载荷比La。可见，充分供油条件下，钢-钢接触副的膜厚比最低，载荷比最高，Si3N4-Si3N4接触副的膜厚比最高，载荷比最低；乏油条件下，3种接触副的膜厚比与载荷比大小则与充分供油时规律相反。说明充分供油时Si3N4-Si3N4接触副润滑性能较好，乏油条件下钢-钢接触副润滑性能较好。但由于Si3N4陶瓷具有自润滑性且具有耐高温、耐腐蚀等特点。因此，对于乏油工况下的Si3N4陶瓷材料的润滑性能还需要进一步研究。

表3 3种接触副在不同供油条件下膜厚比与粗糙峰接触载荷比(U0=4×10-11，W0=6×10-5)

3.4 环境黏度的影响

图7示出了在U0=4×10-11、W0=6×10-5，供油量分别为3.0和0.6 μm工况下，油膜厚度、总压力、粗糙峰压力和油膜温度随环境黏度的变化。可以看出，随着黏度的增加，油膜厚度逐渐增大。这是因为黏度越大，润滑油成膜能力越强，所以膜厚增大。从图中还可以看出，随着黏度增大，总压力基本没变，粗糙峰压力减小。与乏油条件相比，充分供油时油膜厚度随黏度变化增加更明显一些，说明充分供油时黏度对润滑性能影响更明显。不同供油条件下油膜温度都随着黏度的增加而增加，这是因为黏度越大，分子间流动阻力变大，所产生的热量增加，使得油膜温度升高。

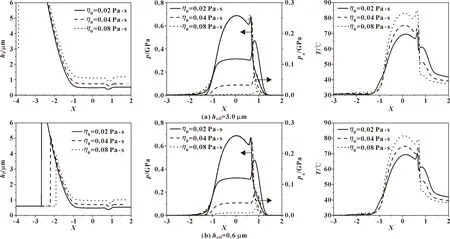
图7 不同供油条件下油膜厚度、压力、油膜温度随环境黏度的变化(U0=4×10-11，W0=6×10-5)

图8示出了在U0=4×10-11、W0=6×10-5工况下，膜厚比λ与粗糙峰接触载荷比La随环境黏度的变化。可见，较小的黏度对应的膜厚比较小，载荷比较大，这正好对应了上述较小的黏度在相同工况下的油膜厚度较小，也能解释黏度较小时粗糙峰压力较大的原因。随着黏度的增加，膜厚比逐渐增大，载荷比逐渐减小。与乏油条件相比，随着黏度的增加，充分供油时的膜厚比增加趋势更明显，载荷比降低速度更快，接触区更容易处于全膜润滑状态。

图8 不同供油条件下膜厚比与粗糙峰接触载荷比随环境黏度的变化(U0=4×10-11，W0=6×10-5)

4 结论

(1)随着供油量的增加，膜厚比增加，粗糙峰接触载荷比减小，最小膜厚与中心膜厚增大，平均摩擦因数减小，油膜最高温度增加，最终都趋于一个稳定值，达到充分供油状态。

(2)对于钢-钢、钢-Si3N4和Si3N4-Si3N4接触副，钢-钢接触副的总压力与油膜温度最低，Si3N4-Si3N4接触副的总压力与油膜温度最高。但在充分供油时，Si3N4-Si3N4接触副油膜厚度较高，膜厚比最高，载荷比最低；乏油条件下，钢-钢接触副油膜厚度略高，膜厚比最高，载荷比最低。

(3)随着速度或环境黏度的增加，油膜厚度增加，总压力基本不变，粗糙峰压力减小，膜厚比增大，载荷比减小。与充分供油相比，乏油条件下的混合润滑性能较差。