端面粗糙度对螺旋浅槽机械密封液膜空化的影响*
陈汇龙 程 谦 韩 婷 付燕霞 周 涛 赵斌娟 杨敬江
(1.江苏大学能源与动力工程学院 江苏镇江 212013;2.上海凯泉泵业(集团)有限公司-镇江水力研究中心 江苏镇江 212013;3.江苏大学国家水泵及系统工程技术研究中心 江苏镇江 212013)
液膜空化是液体润滑轴承、机械密封备受关注和研究的现象。关于空化边界条件的确定,DOWSON和TAYLOR[1]针对轴承列出了Sommerfeld、Reynolds、Half-Sommerfeld和Jakobsson-Floberg-Olsson(JFO)等4种边界条件。NAU[2]在阐述了“蒸汽转变”和“空化”的区别及其相似性的同时,提出了液膜空化边界的解析计算方法。ELROD[3]研究认为Sommerfeld边界条件因与工程实际不符而很少被采用。之后,顾永泉[4]介绍了机械密封端面液膜空化现象、空化边界的确定及其计算方法。潘晓梅等[5]分别运用Reynolds、Half-Sommerfeld和JFO边界条件研究了多孔端面机械密封(LST-MS)端面液膜空化现象,发现采用Half-Sommerfeld边界条件的预测精度很差,而采用另2种边界条件的预测精度十分接近。XUE等[6]研究发现JFO边界条件预测的分离速度比Reynolds边界条件预测结果更接近实验值。
在机械密封空化特性研究方面,QIU、WANG等[7-8]以LST端面密封为对象,研究了凹坑空化现象,实验观测到了明显的同心环状汽化区。胡纪滨等[9]对径向直线槽端面液膜空化进行研究发现空化区域面积随槽深的增大而减小。CHEN等[10]基于多相流空化模型和动网格技术,研究了动压型机械密封间隙液膜空化特性。郝木明等[11]针对螺旋槽上游泵送机械密封研究了工况参数对空化效应和密封性能的影响规律。李振涛、杨文静等[12-15]基于JFO空化边界条件,研究揭示了螺旋槽造型密封端面空化机制、槽型参数对空化的诱发关系和空化对液膜稳态特性的影响规律。陈汇龙、王彬等人[16-17]研究获得了空化热特性和微尺度效应对机械密封性能的影响规律。吉华等人[18]揭示了空化效应和动压效应对微孔端面密封泄漏量的影响规律。马学忠、孟祥铠等[19-20]基于空化效应研究了螺旋槽机械密封泄漏控制机制和液膜动力学特性。陈文杰等[21]研究了织构化圆孔端面密封表面粗糙度对泄漏量和空化区域的影响。许晓东等[22]确定了Lee相变传质方程中最优传质系数,并利用CFD方法研究螺旋槽的槽型结构参数对液膜机械密封汽化特性的影响规律。
综上可见,国内外相关专家学者已在机械密封液膜空化边界确定、空化特性等方面开展了大量研究并取得了诸多成果,但大多是基于端面光滑的宏观空化研究,对于涉及表面粗糙度引起的微观空化的相关研究较少。本文作者以螺旋槽上游泵送机械密封为研究对象,建立涉及表面粗糙度的间隙液膜空化计算模型,研究密封端面不同部位表面粗糙度对液膜空化及流体动压效应的影响。
1 模型建立
1.1 物理模型
文中研究对象为螺旋浅槽机械密封,其动环端面造型示意图见图1。图中,ro、rg和ri分别为端面外半径、外槽根圆半径和内半径;θw、θg分别为密封堰、螺旋槽对应的圆心角;螺旋槽型线为对数螺旋线,θ为螺旋角,其表达式为
r=ri·eφ·tanθ
(1)
式中:r和φ为极坐标下螺旋线上任意点的两个坐标变量。
表1所示为密封运行工况及密封端面几何参数。密封介质为常温清水,动、静环材料分别为碳化硅、碳石墨。因螺旋槽周向均布,故取1/Ng液膜为求解域,其周期性边界条件为

表1 密封端面运行工况及几何参数
φ(θ+2π/Ng)=φ(θ)
(2)
考虑到密封动、静环材料及端面加工工艺等差异,参考文献[23-24],将动环开槽区、动环非槽区和静环端面的粗糙度标准差σ1、σ2和σ3的范围分别取为0.2~1.4 μm、0.03~0.18 μm和0.08~0.38 μm。
鉴于表面粗糙度结构的随机性、复杂性,以及端面径向、周向与轴向在尺度上的跨度较大等因素,会给间隙液膜内流场数值模拟带来极大困难,文中作为前期研究,假定以规则四方体粗糙微元近似代替随机粗糙度,建立了密封微间隙涉及粗糙度的液膜流动计算模型。
规则粗糙表面建模及网格生成方法为:采用Pro-E软件进行计算域端面造型;利用ICEM拓扑功能将端面细化成微元织构面并进行相关定义,比如动环开槽区粗糙度模拟,如图2所示,沿槽区周向复制N条螺旋槽型线作为分割线,由于螺旋线长度与槽周向弧长较为接近,则沿槽区径向复制N条槽内径侧圆弧线作为分割线,至此将槽区划分为N×N个织构微元,其中每个粗糙微元的高度代表粗糙度轮廓的标准差,从而获得近似的螺旋槽底粗糙表面,并采用相同方法获得其他部位的粗糙表面。然后,在所构建的微元织构面生成面网格,再利用ICEM拉伸功能将面网格拉伸成体网格,槽区液膜、粗糙微元液膜和间隙液膜分别拉伸4层、3层和3层。
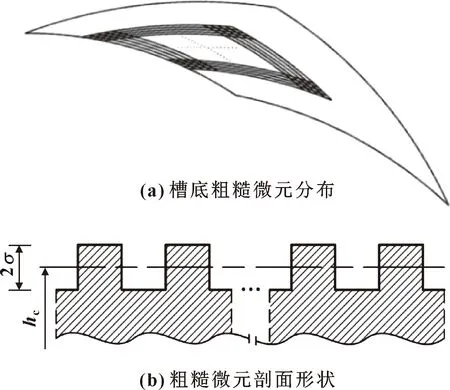
图2 粗糙微元及粗糙表面模拟示意
1.2 数学模型
综合考虑模拟计算的复杂性、精确性和效率,文中依据密封微间隙润滑膜特点作如下假设:
(1)忽略密封介质重力;
(2)文中着重考察端面粗糙度对液膜空化的影响规律,暂未考虑环变形的影响;
(3)间隙流体与壁面间无滑移;
(4)液膜温度和黏度为定值。
依据文中密封结构参数和所涉及的最大转速计算可知,润滑膜流动因子α[25]远小于600/1 600,故密封微间隙液膜流态为层流。
对于间隙液膜空化问题,因两相边界无法明确定义,故采用如下混合物模型:
混合连续性方程
(3)
混合动量方程
(4)
汽相和液相间的质量传输由质量输运方程控制:

(5)
式中:αv为平均汽相体积分数;Re和Rc分别为空化过程中的蒸发相和冷凝相的源项。
文中选用Zwart-Gerber-Belamri空化模型,采用SIMPLEC算法,压力离散格式采用PRESTO!,动量采用二阶迎风差分格式,体积分数采用QUICK格式。边界条件设置如图3所示。
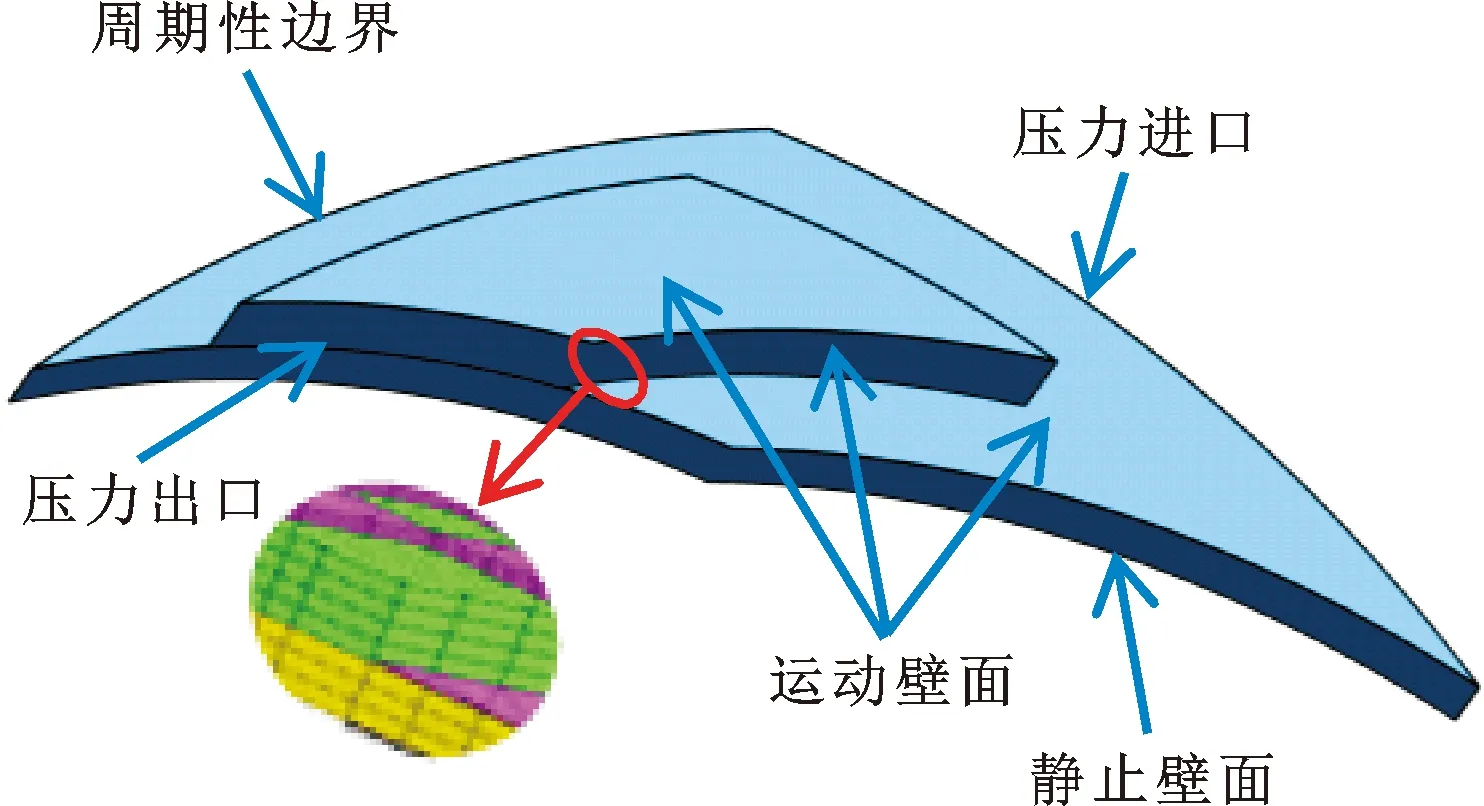
图3 液膜边界条件
1.3 粗糙微元数目确定及网格无关性检验
文中在粗糙微元数目确定、网格无关性检验和后续的计算结果分析中,考虑某部位的粗糙度影响时,均假设其他部位为光滑表面。
以规则粗糙微元表征实际粗糙度时,存在粗糙微元大小的取值问题,现以动环槽区粗糙为例加以分析。在介质压力pi为0.3 MPa、转速n为5 000 r/min、槽区粗糙度标准差σ1取为0.8 μm情况下进行计算,得到如图4所示液膜开启力F和泄漏率Q随分割线数N的变化规律。可见,当N达到100即槽区粗糙微元数目达到10 000个及以上时,液膜开启力F和泄漏量Q的变化很小。因此,文中的槽区粗糙度模拟选取N=100,非槽区和静环端面粗糙度模拟根据区域面积的相对大小选取N=200。
文中分别对槽区、非槽区和静环端面进行网格划分(局部网格放大如图3所示)并进行了网格无关性检验。模拟分析结果表明:当槽区、非槽区和静环端面单周期网格数量分别达到1 576 243、2 638 155和3 974 081以上时,F和Q受网格尺寸的影响很小,故以此3个网格划分方案进行模拟计算。动环槽区不同粗糙度时密封性能参数值随网格数量的变化规律如图5所示,限于篇幅,动环非槽区和静环端面不同粗糙度时的模拟结果不一一列出。

图5 动环槽区不同粗糙时密封性能参数值随网格数量的变化规律
2 模型验证
图6示出了采用文中所建立计算模型(动、静环端面均考虑粗糙度)对文献[26]的研究对象进行摩擦功耗计算的结果,以及与文献[26]的实验及模拟结果的对比。文献[26]通过摩擦功耗实验验证了所提出的非接触液膜润滑机械密封摩擦功耗计算公式。

图6 文中计算结果与文献[26]的对比
由图6可见,文中计算得到的摩擦功耗与文献[26]的计算结果具有较好的一致性,且文中计算结果处于文献[26]计算结果的偏实验值一侧,这是因为文中计算模型考虑了表面粗糙度,导致润滑膜边界附近的流动受凹凸表面扰动而趋于复杂化,流动损失增加且随转速增大而趋于明显。由此表明文中计算模型是可靠的。
3 计算结果与分析
对于螺旋浅槽上游泵送机械密封,无论是端面螺旋槽造型还是表面粗糙度均可能在液膜流动方向上形成发散-收敛交替通道,为空化的产生提供了必要条件,因此可能既存在宏观空化又存在微观空化。由于密封端面不同部位的粗糙度大小不同及其对空化的影响也可能不同,故以下分别就动环槽区、动环非槽区以及静环端面等3个部位为不同粗糙度时探讨液膜空化特性。
3.1 动环槽区粗糙度对液膜空化的影响
介质压力0.6 MPa、转速8 000 r/min时不同动环槽区粗糙度下端面压力分布云图如图7所示。可以看出,泵送槽的宏观结构形成的泵送效应及动压效应使液膜形成了明显的高、低压区,当槽区粗糙时,随着粗糙度的增大,外槽根高压区的压力及范围略有增大,说明槽区粗糙度有提升膜压的作用。为了更具体地考察粗糙度的影响,将内径侧槽堰低压区进行局部放大并置于分度更小的坐标中(因布图不便未将小图坐标放入)。由局部放大图可见,槽区粗糙微元使槽区内径侧附近膜压提升并出现与粗糙微元分布一致的高低压交替分布现象,且粗糙度越大越明显,说明粗糙度引起了动压效应。

图7 不同动环槽区粗糙度值下的压力分布
介质压力为0.6 MPa,不同转速时密封间隙液膜汽相分布随粗糙度变化云图如图8所示,对应工况下液膜平均汽相体积分数随动环槽区粗糙度变化规律如图9所示。当转速为1 000 r/min时,从图8(a)、图9可看出,无论槽区是否粗糙,液膜汽相体积分数为0,说明液膜内部流速小,螺旋槽和粗糙微元均未导致空化的发生,密封面处于全液体润滑状态。由图8(b)、(c)和图9可以看出,转速增大时,螺旋槽背风侧附近出现局部高汽相体积分数区域且随转速的增大而加剧,说明转速增大,槽的泵送效应和动压效应明显增强,液膜空化程度提升;而随着槽区粗糙度的增大宏观空化区域略有缩小,汽相体积分数降低且转速越高降低越明显。由图8(c)中局部放大图并结合图7可见,在槽背风侧附近粗糙微元引起了局部微空化,说明粗糙微元产生了动压效应,提升了膜压,降低了宏观空化程度,对液膜空化产生了一定的抑制作用。
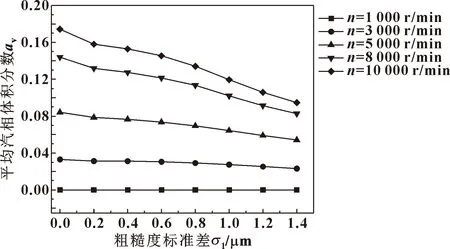
图9 不同转速下动环槽区粗糙度值对液膜平均汽相体积分数的影响
3.2 动环非槽区粗糙度对液膜空化的影响
介质压力0.6 MPa、转速8 000 r/min时端面膜压分布随动环非槽区粗糙度变化云图如图10所示。可以看出,动环非槽区粗糙度使外槽根高压区的压力明显提升并向槽、堰、坝区明显拓展。从局部放大图可见,非槽区粗糙度明显导致液膜出现高低压交替分布,而且随着粗糙度增大高压区增强越明显。这说明非槽区液膜流体以周向高速流动为主,粗糙度引起的流体动压效应更突出,局部出现了微观空化;此外,坝区粗糙度也给高转速导致的负泄漏流带来摩阻的增大,这也是高压区明显增强的原因之一。
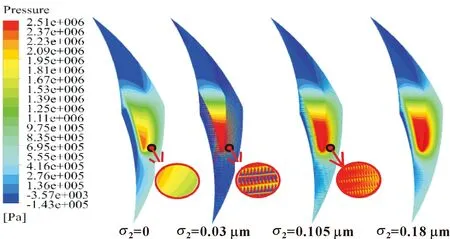
图10 不同动环非槽区粗糙度值下的膜压分布
介质压力为0.6 MPa,不同转速时间隙液膜汽相分布随动环非槽区粗糙度变化云图如图11所示,相应工况下液膜平均汽相体积分数随动环非槽区粗糙度的变化规律如图12所示。从图11、图12可以看出,低转速1 000 r/min时,非槽区粗糙度并没有改变端面光滑时液膜汽相体积分数很低的状态,宏观空化和微观空化均无发生;转速增大时,槽堰区出现明显的空化区域且随转速升高空化区域增大、汽相体积分数提升,螺旋槽泵送效应和动压效应均增强。

图11 不同转速下动环非槽区粗糙度对液膜汽相分布的影响
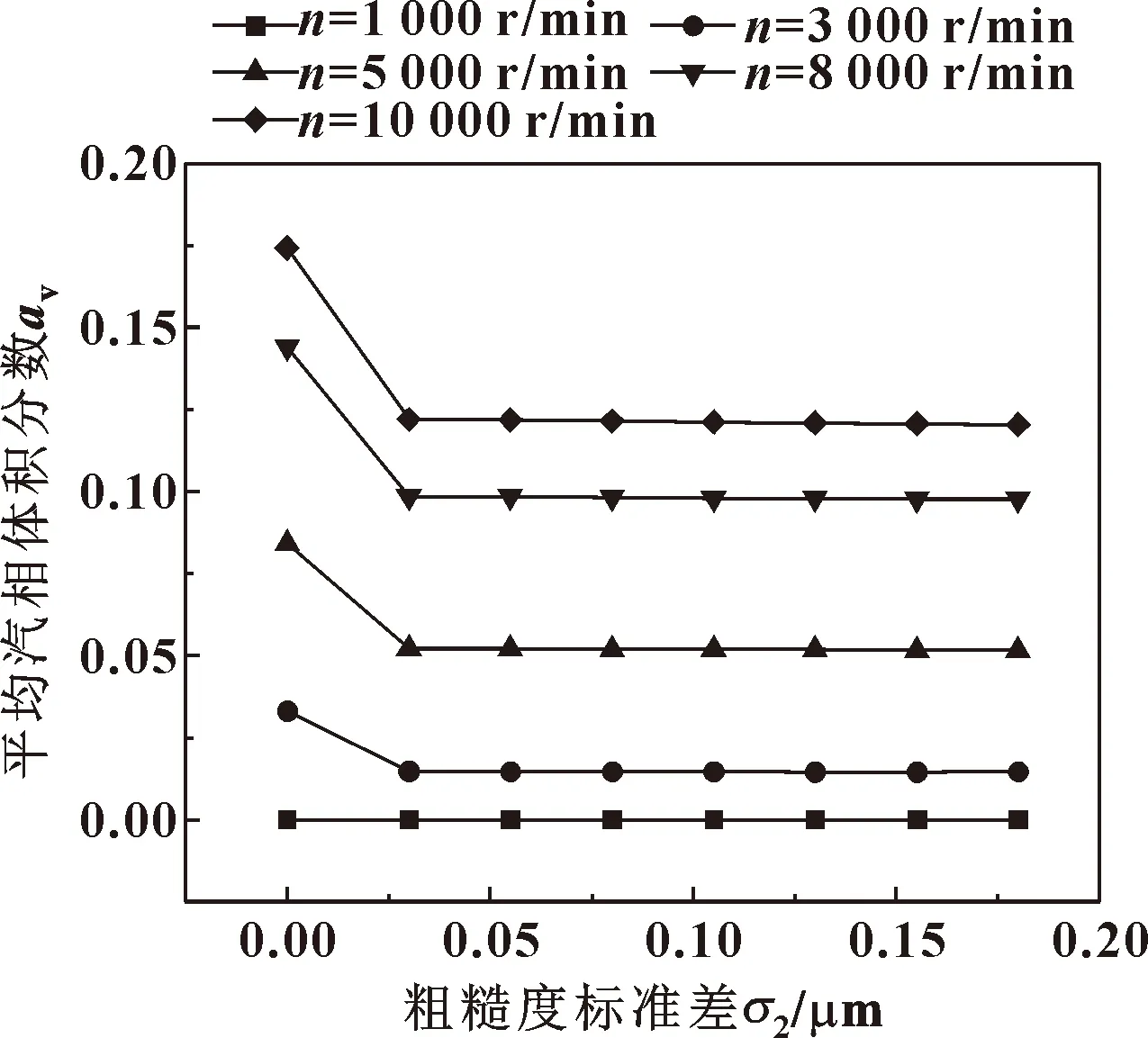
图12 不同转速下动环非槽区粗糙度值对液膜平均汽相体积分数的影响
结合图10可看出,在较高转速下,粗糙微元导致的膜压升高,使空化区域收缩,汽相体积分数降低,而粗糙度增大对平均汽相体积分数几乎不影响,这说明非槽区粗糙度一方面对宏观空化具有一定的抑制作用,另一方面非槽区中因部分堰区膜压较低,粗糙微元引起的微空化导致汽相体积分数轻微增大,而大部分压力相对较高区域中,粗糙微元导致的微空化因压力提升而减弱或消失。
3.3 静环端面粗糙度对液膜空化的影响
介质压力0.6 MPa、转速8 000 r/min时,膜压分布随静环端面粗糙度变化云图如图13所示。可以看出,静环端面粗糙时,液膜高压区向槽、坝区拓展,压力值升高,且粗糙度越大趋势越明显,粗糙微元引起的微弱高低压交替分布覆盖了整个液膜区。这说明静环端面粗糙微元在导致液膜流体产生动压效应、提升膜压的同时,同样增大了坝区负泄漏流动的摩阻,这些均是致使高压区膜压增强的因素。
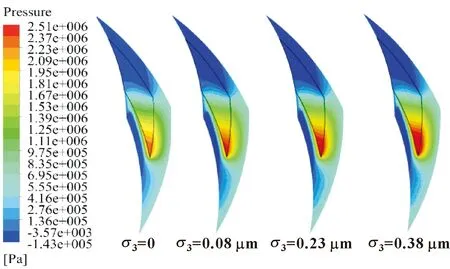
图13 不同静环端面粗糙度值下的膜压分布
介质压力为0.6 MPa,不同转速时液膜汽相分布随静环端面粗糙度变化云图如图14所示,对应工况下液膜平均汽相体积分数随静环端面粗糙度变化规律如图15所示。从图14、图15可以看出,低转速1 000 r/min时,与前述其他区域粗糙时的情况相同,无论是否考虑静环端面粗糙度,整体计算域汽相体积分数为0,说明宏、微观空化均未发生。转速增大时,槽堰区液膜局部出现空化且随转速增大空化程度加剧;转速不变时,较小的静环端面粗糙度使液膜空化程度减弱,平均汽相体积分数有所降低,随着粗糙度的增大空化程度有所增强。可见,静环端面粗糙对液膜空化的影响是整体性、综合性的,小粗糙度时,因泵送流摩阻增大而使宏观空化减弱,且低压区粗糙微元微观空化也弱,故总体空化程度减弱;随着粗糙度的增大,液膜低压区粗糙度引起的微观空化加剧,使整体空化程度有所回升;总体上静环端面粗糙度对液膜空化的影响相对较小。
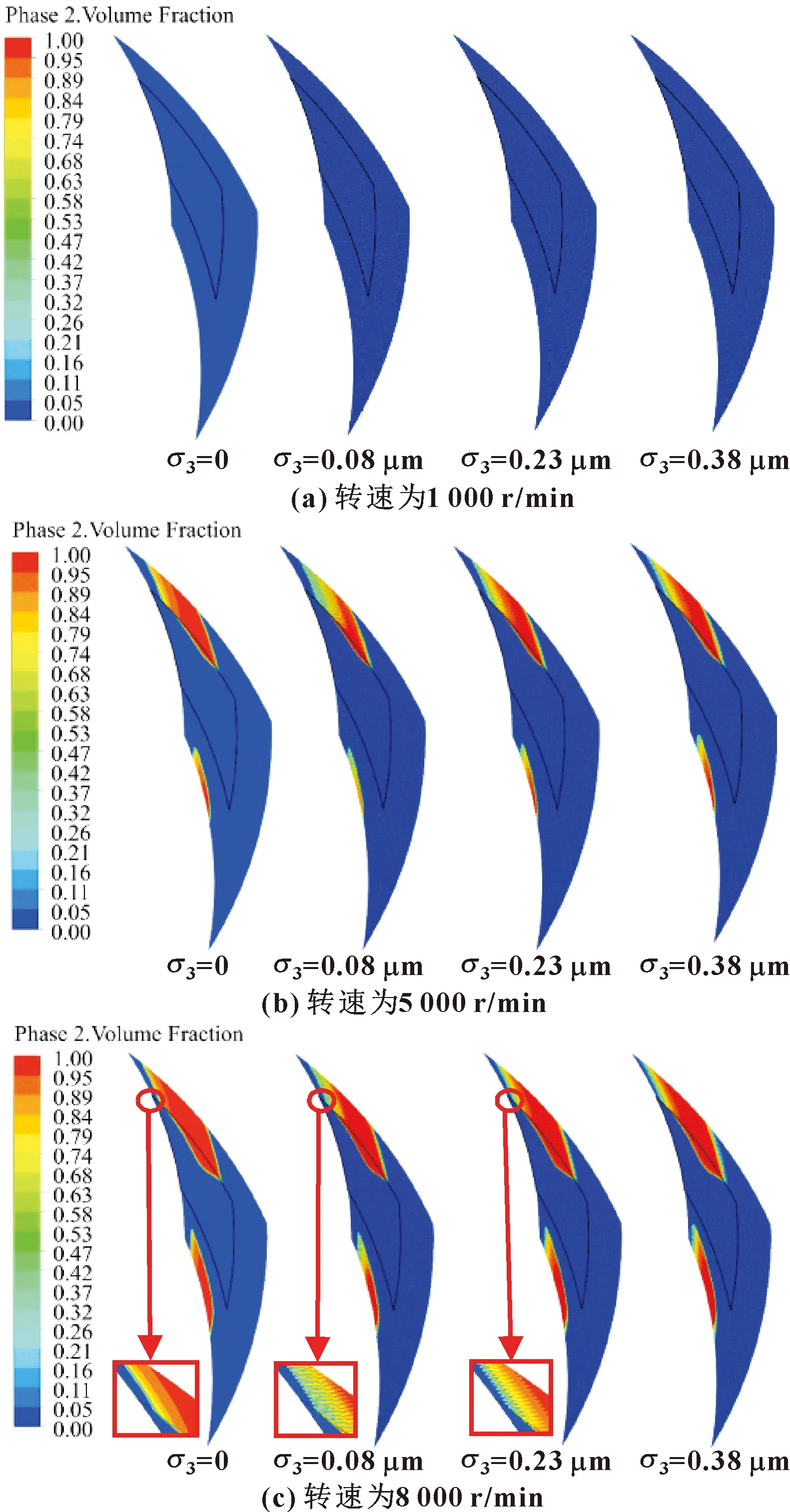
图14 不同转速下静环端面粗糙度值对液膜汽相分布的影响

图15 不同转速下静环端面粗糙度值对液膜平均汽相体积分数的影响
综上所述,密封端面3个不同区域表面粗糙度对膜压分布、液膜空化的影响规律是不一样的。
3.4 动静环端面粗糙度对液膜空化的影响
图16所示为介质压力0.6 MPa,转速1 000~10 000 r/min时,动、静环端面同时考虑粗糙度(取各部位粗糙度中值)与不同部位粗糙度(取中值)情况下的平均汽相体积分数对比。可以看出,当转速低于1 000 r/min时,与局部区域考虑粗糙度相同,动静环全端面考虑粗糙度时,润滑膜的平均汽相体积分数仍为0,说明液膜仍未发生宏、微观空化;当转速高于1 000 r/min时,随转速的增大,润滑膜的平均汽相体积分数不断升高,但动静环全端面考虑粗糙度时的平均汽相体积分数增速比考虑任何局部粗糙度时小,且转速越高越明显,说明各部位粗糙微元产生的动压效应呈现出叠加效应,对微观空化起到了一定的抑制作用,且转速越高粗糙微元的动压效应越明显,抑制作用也越强。
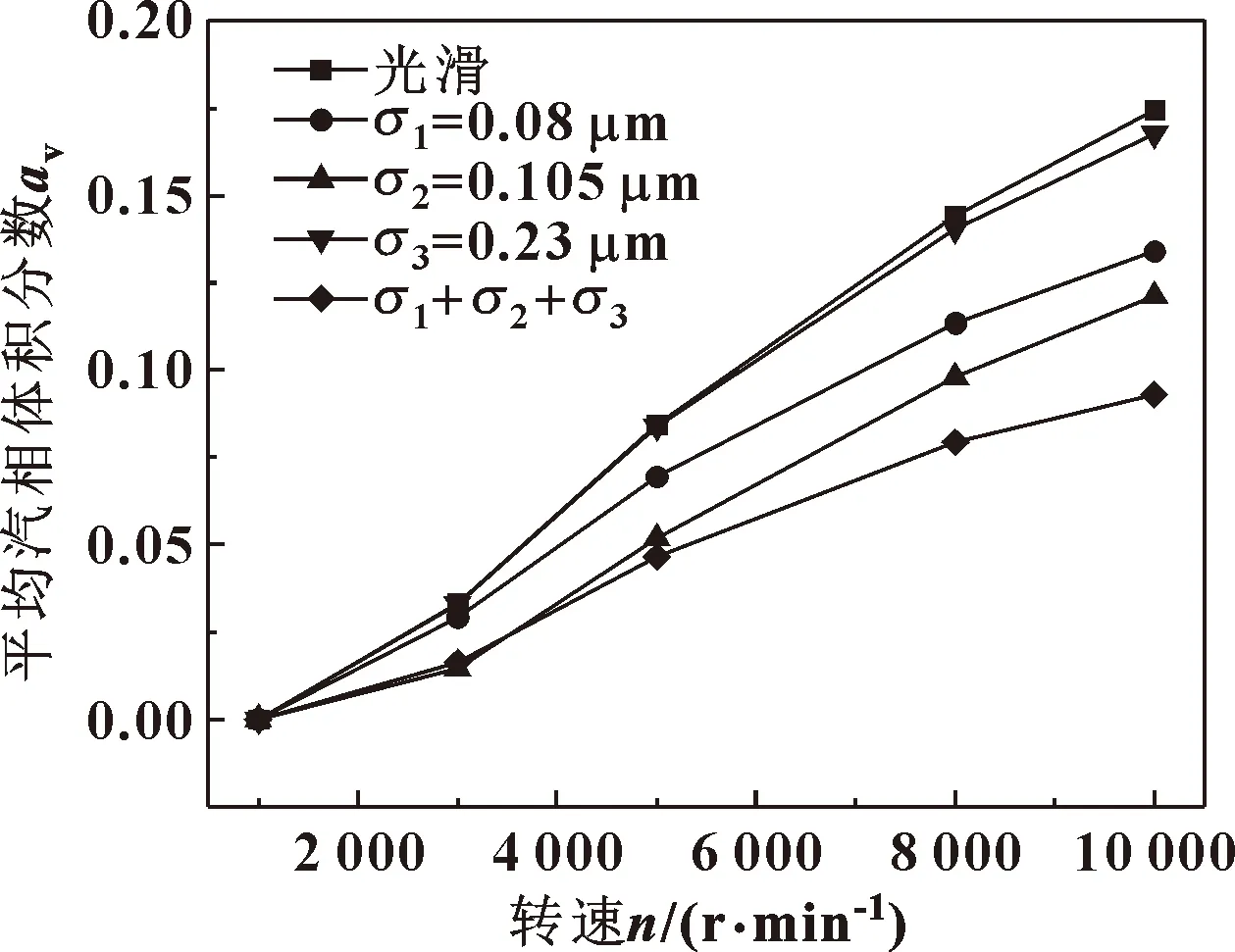
图16 不同转速时全端面粗糙度值对液膜平均汽相体积分数的影响
对图16及图9、图12、图15综合分析可知,粗糙微元对液膜空化的抑制作用从大到小的顺序为:动静环全端面、动环非槽区、动环槽区、静环端面。其原因与粗糙区域大小和所在区域的膜压、流速大小有关,高速高压区粗糙度对膜压的“贡献”更大,对空化的抑制作用较明显,高速低压区粗糙度对空化的“贡献”更明显,对膜压“贡献”较弱,低速区(槽区)粗糙度的影响相对较小。
4 结论
(1)动环槽区粗糙度增大,外槽根高压区的压力及范围略有增大,膜压提升;动环非槽区粗糙度使外槽根高压区的压力明显提升并向槽、堰、坝区明显拓展,且粗糙度越大高压区增强越明显;静环端面粗糙时,液膜高压区向槽、坝区拓展,压力升高,且粗糙度越大趋势越明显。
(2)低转速(如1 000 r/min)时,无论端面粗糙与否,液膜平均汽相体积分数为0,螺旋槽和粗糙微元均未导致空化;端面粗糙区液膜出现与粗糙微元分布一致的高低压交替分布。
(3)较高转速时,位于较低膜压区的粗糙微元会导致液膜微观空化;动环槽区粗糙度增大宏观空化区域略有缩小、空化程度降低,对液膜空化产生了一定的抑制作用;动环非槽区粗糙微元导致膜压升高、空化区域收缩,但粗糙度增大对平均汽相体积分数几乎不影响;较小的静环端面粗糙度使液膜空化程度减弱,平均汽相体积分数有所降低,随着粗糙度的增大空化程度有所增强,但总体上静环端面粗糙度对液膜空化的影响相对较小。
(4)动、静环全端面粗糙时各部位粗糙微元产生的动压效应呈现出叠加效应,对空化的抑制作用比任何局部粗糙时强,且转速越高越明显。

