核主泵系统高温液态铅铋润滑导轴承流体动力学特性分析*
解忠良 焦 见 杨 康 符江锋 何 涛
(1.西北工业大学工程力学系 陕西西安 710072;2.西安电子科技大学机电工程学院 陕西西安 710071;3.西北工业大学动力与能源学院,动力控制装置性能及可靠性研究所 陕西西安 710072;4.武汉第二船舶设计研究所 湖北武汉 430205)
铅铋轴承是新一代核电站二回路主循环系统重要组成部分,用于支撑整个二回路主循环系统轴系。铅铋轴承是新式合金轴承,与国内现役核电站所用轴承有所不同。鉴于铅铋轴承自身结构以及液膜的复杂程度和流体动力学特性尚不清晰,将很大程度上影响整个二回路循环系统的稳定性,抗冲击性和抗振动性,进而影响整个系统使用寿命。目前国内对铅铋轴承的了解尚不深入,对轴承润滑机制和液膜流体动力学特性尚不清楚。因此,研究该类新型高温液态金属润滑轴承润滑机制,丰富流体动压润滑理论,可为该类特种轴承设计研发及国产化提供理论依据。
国内学者对低黏度介质润滑滑动轴承进行了大量研究。何阳等人[1]研究了网状表面织构对水润滑轴承摩擦性能的影响,发现在忽略空蚀的条件下,同一转速下水膜承载能力基本随着网纹深度的增加先增大后减小。周广武等[2]建立多沟槽润滑结构和实际工况边界条件的水润滑橡胶合金轴承弹流润滑数学模型,计算了有无沟槽以及沟槽半径对润滑性能的影响,计算结果表明:在沟槽处膜厚较大,压力较低,而在承载区膜厚较小,压力较高,周向方向上压力分布不连续,并且在最小膜厚处轴向方向的入口和出口附近出现了2个压力峰值;水膜压力和最小膜厚均随沟槽半径的增大而减小;承载能力随偏心率增大而增大,随沟槽半径和过渡圆弧半径的增大而减小;摩擦因数随转速增大而略有增大,随沟槽半径的增大显著增加。王艳真等[3]研究了水润滑尾轴承数值计算过程中的边界条件和润滑介质的流动状态,建立了计入弹性变形的轴承润滑性能分析方法。张飞等人[4]针对某艉轴工作时出现的下沉现象以及伴随的强烈刺激噪声展开研究,通过数值分析等方法,提出了改进轴承结构、优化材料性能的解决方案。XIE等[5]研究了偏差对润滑性能的影响和水润滑轴承的润滑状态转换,结果表明:随着最大压力和剪切应力的增大,最小膜厚减小,存在偏差角的8个动态系数增大。张凌峰等[6]利用Fluent软件,研究比较了轴瓦螺旋槽轴承和主轴螺旋槽轴承的性能,探讨了螺旋槽头数、角度以及槽台宽比对轴承间隙流域流体的泄漏量、支反力和偏位角的影响,揭示了影响导轴承性能的主要和次要因素。曹金龙[7]研究了液钠动静压轴承的润滑机制和动态特性,改进了轴承结构,提高了轴承承载力,减少液钠泄漏量和泵轴与轴承内壁面直接摩擦造成的剧烈磨损。王晓红等[8]针对外界异物可能对轴瓦造成损伤,通过建立流体润滑模型,对比了多种情况下异物磨损对轴承润滑性能的影响。王占朝等[9]通过建立考虑轴承受到多种因素影响的瞬态模型,分析探讨了多种因素影响下轴承在平衡梁结构与非平衡梁结构的运转与停止过程,实验结果给出了解决轴承启停转速的最佳方案。陈汝刚等[10]利用ARMD研究了液钠动静压轴承润滑机制和动态特性,揭示了钠泵流体动静压混合润滑轴承润滑机制的特殊性。裴世源等[11]建立了钠泵导轴承润滑分析模型,分析了工况参数与关键结构参数对润滑特性的影响。VON GESSENECK等[12]针对轴承在铅铋共晶冷却剂中面临的工况条件,提出一种远程监测铅铋共晶的方法,讨论了润滑不足对轴承工况的影响。HAJRA等[13]提出了一种利用钛酸铋、Bi4Ti3O12(BiTiO)/聚二甲基硅氧烷(PDMS)复合薄膜的摩擦电和压电效应的多单元混合压电-摩擦电纳米发电机(HNG);随后,在3D打印结构和球体的帮助下,构建了一种新的器件结构设计,包括一个多单元HNG器件,分别提供300 V和4.7 μA的电压和电流输出;最后,将HNG装置用于生物力学能量收集,并为LED、计算器和手表等各种电子设备供电。ZHANG等[14]针对加速器驱动系统主冷却液回路的核心部件——液体铅铋泵,设计了一种液体铅铋泵,并对其性能和流动特性进行了数值模拟,研究了输送介质对泵性能的影响以及对液压元件的作用力,结果表明,用液体铅铋代替水介质,提高了泵的运行性能。
本文作者在前期研究的基础上[15-17],采用流体动静压润滑原理,对新一代核电站二回路主循环系统的铅铋轴承进行仿真分析,研究间隙、偏心率、转速和环形导流槽等因素对轴承流体动力学特性的影响,厘清了转速和偏心率与压力峰值之间的关系,探明了间隙等因素对轴承各项润滑性能参数的影响机制,阐明了环形导流槽对轴承润滑性能的影响机制;在此基础上,有效揭示了该类轴承的流体动力学润滑机制,从而为铅铋轴承在国内新一代核电站中的应用提供理论依据。
1 理论模型
1.1 CFD控制方程
(1)质量守恒方程
单位时间内微小流体六面体单元中质量的增加,与相同时间内流入六面体单元的净质量相等。转轴在铅铋合金润滑液环境中工作,根据润滑液的性能,得出方程[18]如下:
(1)
该方程适用于可压缩流体和不可压缩流体,其中ρ为流体密度,t为时间,Sm是连续相的质量。铅铋合金润滑液属于不可压缩流体,所以微分方程[18]如下:
(2)
式中:ux、uy、uz为流体模型于t时刻在点(x,y,z)处的速度分量。
(2)能量守恒方程
微小流体六面体单元中能量的增加率为流入微小六面体单元的热流通量及体积力与表面力的总和。转轴工作时产生的热大部分会被润滑液吸收,只有少部分反作用于自身,微分方程[18]如下:
(3)
式中:U是单位体积内的热能;mij是表面张力;υ是移动距离;k是热传导系数;q是单位质量的热量分布函数;p是单位体积上的压力。
(3)动量守恒定律
微小流体六面体单元的动量变化率与外界作用在该六面体单元的各种力之和相等。转轴系统运行过程中,会有微小碰撞冲击,对铅铋轴承造成一定的损伤,其动量守恒方程[18]如下:

(4)

(5)
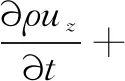
(6)
式中:∂τxx、∂τyy、∂τzz是应力张量;fx、fy、fz是外部体积力。
1.2 铅铋合金润滑液物性模型
LBE合金的共晶成分为55.5%Bi和44.5%Pb(质量分数),常压下,其熔点为125 ℃,沸点为1 677 ℃[19-21]。
铅铋轴承流体域为铅铋合金润滑液,液态铅铋的密度计算公式[20]为
ρ=11 096-1.323 6T
(7)
式中:T为液体LBE介质温度,K。
液态铅铋的动力黏度计算公式[20]为
μ=4.94×10-4×e754.1/T
(8)
液态铅铋的比热容计算公式[20]为
cp=159-2.72×10-2T+7.12×10-6T2
(9)
液态铅铋的热导率计算公式[20]为
(10)
液态铅铋的表面张力计算公式[20]为
f=0.437-6.6×10-5T
(11)
液态铅铋的绝热弹性模量计算公式[20]为
Bs=(35.18-1.541×10-3T-9.191×10-6T2)×109
(12)
计算模型中的铅铋合金润滑液工作温度为额定工况温度310 ℃,代入得:ρ=10 324.14 kg/m3,μ=1.8×10-3Pa·s,cp=145.56 J/(kg·K),λ=12.3 W/(m·K),f=0.39 N/m,Bs=3.12×1010Pa。
2 CFD模型
2.1 轴承结构
铅铋轴承是新型立式轴承,其模型结构如图1所示。区别于传统轴承,铅铋轴承内壁面周向均匀分布8个工作腔室,每个腔室中央开有导向孔,其可将铅铋合金润滑液引入腔室中。内壁面底端有环形导流槽Ⅰ和环形导流槽Ⅱ,在轴承支撑转轴运行时起到泄压作用。外壁面均匀分布8条螺旋槽,每条螺旋槽与内壁面工作腔室导向孔相对应,对应序号为:1-9、2-10、3-11、4-12、5-13、6-14、7-15、8-16。螺旋槽可循环地将合金润滑液由工作腔室输送到轴承底端环形导流槽处。

图1 铅铋动静压轴承结构
通过SolidWorks构建铅铋轴承液膜模型,实际模型如图2(a)所示。已有研究表明,外部螺旋槽对轴承性能影响较小[15]。因此,根据模型特性,对其进行合理简化。得到图2(b)所示简化后的液膜模型,表1给出了简化后液膜模型具体结构参数。
2.2 边界条件及网格划分
铅铋轴承区别于其他轴承之处在于:润滑入口端为8个工作腔室,如图3。8个沟槽沿外壁面均匀分布,入口即为图中箭头垂直指向沟槽面处,一共8个入口,铅铋合金润滑液由此进入,液膜内壁面为旋转面,外壁面为静止面,液膜上下端面为出口端。

图3 边界条件示意
网格质量的高低与数量的多少决定着计算的精度和效率。与四面体网格相比,六面体网格质量相对较好,计算速度快、精度高、收敛性好。对液膜模型进行网格划分,首先进行面的修补和边界条件的定义,其次建立块结构,通过O-grid划分,实现每个沟槽与块的对应,最后进行点映射和线映射,以及全局网格尺寸的定义,最终得到整体网格。沿流体膜厚度方向划分5层网格,网格数量达到1 266 860,最小网格平均质量为0.976。经过6组网格划分对比试验后表明,在出、入口端划分5层网格时,液膜压力趋于稳定且在此时网格数量相对较少。图4给出了网格划分完成后整体六面体网格示意图,从图中可见,出口端面有5层网格,整体均是六面体网格,具体网格参数如表2所示。

图4 铅铋轴承液膜网格示意

表2 网格参数
2.3 仿真过程
图5给出了铅铋轴承整体计算流程。从划分网格、对液膜进行初始值赋予开始,从而进行液膜流动状态的判断以便选择求解模型。设置边界条件和求解液膜连续性方程,最终得到液膜的极值压力、承载力和摩擦因数等。

图5 铅铋轴承液膜计算流程
3 结果与讨论
在对铅铋轴承流体动力学模型进行分析时,作如下假设:
(1)由于温度一定时,液态金属合金随着流速的变化,物理性能参数与水非常接近,所以液态金属合金为牛顿流体;
(2)满足界面无滑移条件;
(3)分析铅铋轴承仅考虑其径向运动,膜厚和压力由于轴向梯度变化忽略不计,仅分析各自径向梯度变化。
3.1 环形导流槽对润滑性能的影响规律
图6和图7分别给出了偏心0.2、间隙0.2 mm,考虑环形导流槽和不考虑环形导流槽2种情况下的压力云图。可明显看出,当考虑环形导流槽时,正压承载区域和负压承载区域聚集在沟槽上方,即环形导流槽所在区域,如图8所示。而不考虑环形导流槽的正、负压承载区,动压效应则集中在沟槽间。造成这一区别的主要原因是环形导流槽与压力入口处的导向孔相同,可以引导压力入口处的铅铋合金润滑液,从而达到泄压作用。此外,根据图7所示,在间隙和偏心率较小时,动压效应尚未完全形成。在此过程中,又因沟槽的阻断,正、负压承载区被分开,从而造成了图7所示的动压效应不稳定情形。

图6 考虑环形导流槽的压力云图

图7 不考虑环形导流槽的压力云图

图8 环形导流槽液膜与轴承对应图
为研究环形导流槽对润滑性能的影响规律,选取典型工况参数:间隙0.2 mm、偏心率0.2,比较有、无环形导流槽情况下,转速对各项参数的影响。图9所示是考虑有、无环形导流槽情况下,转速对极压、承载和摩擦因数的影响。从图9(a)、(b)可看出,环形导流槽存在与否,最大压力都随转速增大而增大,最小压力随转速增大而减小。但转速在100~500 r/min范围内,考虑环形导流槽的最大压力大于不考虑环形导流槽,500~1 000 r/min时情况相反。图9(b)中,转速在100~200 r/min时,无环形导流槽最小压力大于有环形导流槽,200 r/min之后,无环形导流槽的最大负压逐渐减小,有环形导流槽最大负压减小趋势比较缓慢。图9(a)中,考虑环形导流槽压力云图随转速增加时,沟槽上部的正、负承载区逐渐向沟槽间转移,对应了环形导流槽的泄压作用。图9(c)、(d)分别给出了有、无环形导流槽情况下转速对承载力和摩擦因数的影响。可看出,考虑环形导流槽对承载力和摩擦因数的影响远远小于不考虑环形导流槽。无环形导流槽时,承载力和摩擦因数随转速呈指数型增长;考虑环形导流槽时,承载力和摩擦因数随转速几乎线性增长。由此可见,简化环形导流槽对承载力和摩擦有着较大影响,摩擦增大的同时承载也得到大幅度提升。这对提高轴承抗振缓冲性能具有重要启发作用,并为后续工作进一步开展奠定基础。
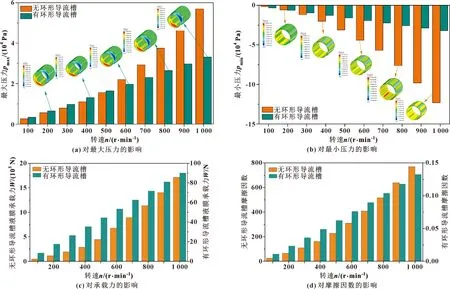
图9 不同转速下环形导流槽对最大和最小压力、承载力、摩擦因数的影响
3.2 沟槽数目对润滑性能的影响规律
为研究沟槽数目对润滑性能的影响规律,选取典型沟槽数目:6沟槽和8沟槽进行分析。考虑到铅铋轴承结构的复杂性,综合分析铅铋轴承对转轴性能的影响,针对铅铋轴承整体结构进行简化,以期实现与原轴承结构的对比,从而完善对铅铋轴承的研究。建立简化后的铅铋轴承模型如图10所示。图10与图1相比,简化了螺旋槽、环形导流槽以及多个导向孔,工作腔室由原来8个减少到6个,加大了轴承厚度。由于动压效应主要形成并集中于沟槽间,所以对液膜模型进行合理简化,简化后的液膜模型在结构上远没有原模型复杂,减少了导向孔。详细参数信息如表3所示。
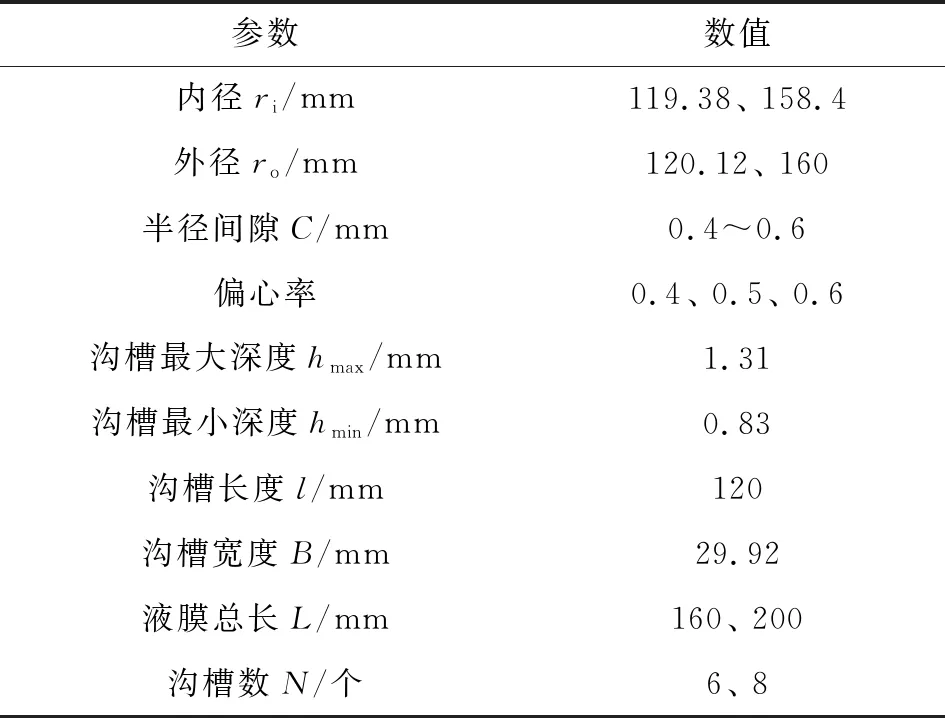
表3 液膜模型结构参数

图10 铅铋动静压轴承结构(简化后)
图11所示是8沟槽与6沟槽在不同偏心下极压、承载和摩擦因数的变化曲线。如图11(a)所示,相同间隙下,最大压力随偏心率增大而增大;不同间隙下,最大压力与偏心率之间亦呈正相关关系。间隙为0.4 mm时最大压力随偏心增长最快,当间隙大于0.4 mm时,最大压力随偏心率增长的趋势逐渐缓慢。同一偏心下,最大压力随间隙增大而减小;相邻两条折线间的压力差也随偏心增大而逐渐拉开差距。此外,从图中可知,8沟槽最大压力远大于6沟槽,并且6沟槽偏心率与最大压力的规律与8沟槽相似。从压力云图可知,随着偏心的增大,8沟槽和6沟槽液膜的动压效应逐渐形成,正、负压承载区各自向一处集中。图11(b)中,相同间隙下,最小压力与偏心率呈负相关关系,最小压力随偏心率增大而减小。不同间隙条件下的最小压力随偏心增大而减小的速率差异较大,间隙越大最小压力减小越缓慢。8沟槽时,相邻两条曲线的压力差随偏心率的增大而增大,且偏心率越大压力差越大。8沟槽与6沟槽的最小压力都随偏心率的增大而减小,且6沟槽最小压力整体比8沟槽大。8沟槽时,最小压力随偏心率减小的同时又随间隙的增大而增大。在图11(c)中,相同间隙下,承载力随偏心率增大而增大,当偏心较低时(0.4~0.5),承载力缓慢增长,偏心较高时(0.5~0.6),承载力则以较快趋势增长。不同间隙下,相邻两条曲线的承载力之差随偏心增大而逐渐拉开差距;同一偏心下,承载力随着间隙的增大而减小。间隙较小时(如0.4 mm),承载力减小较快;间隙较大时(如0.6 mm),承载力则缓慢减小。此外,6沟槽整体承载曲线远低于8沟槽。如图11(d)所示,相同间隙下摩擦因数随偏心率增大而增大;同一偏心率下,摩擦因数随间隙增大而减小,相似的规律亦在不同偏心率情况下体现。8沟槽摩擦因数远大于6沟槽,8沟槽摩擦因数随间隙增大而均匀增长,6沟槽摩擦因数随间隙增大而增长得较快。
综上分析,8沟槽和6沟槽承载力和摩擦因数皆随偏心率增大而增大,但8沟槽承载力和摩擦因数曲线整体大于6沟槽。因此,对沟槽数目而言,存在较大的优化设计空间使得轴承性能达到增载减阻、减振降噪最优,这也是后续研究的重点。
3.3 转速对润滑性能的影响规律
选取典型工况参数:间隙0.3~0.7 mm、偏心率0.8以及转速100~1 000 r/min,研究转速对极压、承载和摩擦因数的影响,如图12所示。
从图12(a)中可以看出,相同间隙时,最大压力随转速增大而增大;转速低于500 r/min时,最大压力几乎呈线性增长,转速高于500 r/min,最大压力则呈指数型急剧增长。间隙不同时,小间隙(如0.3 mm)下最大压力随转速增长速率比大间隙(如0.7 mm)快。同一转速下,最大压力随间隙增大而减小,相邻两条曲线的压力之差随间隙增大而减小,并且在0.3~0.5 mm间隙范围内压力差减小幅度比在0.5~0.7 mm间隙范围内大。这是由于随着间隙增大,液膜最小膜厚变小、最大膜厚变大,动压效应主要在膜厚较小侧形成,而膜厚越小泄压作用越强,压力随之减小。转速不同时,相邻两条曲线间的压力差随转速升高而显著增大。从图12(b)中可看出,在相同间隙条件下,最小压力与转速呈负相关,最小压力随转速增大而减小。不同间隙条件下,最小压力随转速增大而减小的速率差异较大,间隙越大最小压力减小速率越缓慢。同一转速情况下,最小压力随着间隙的增大而增大。在0.3~0.5 mm间隙范围内的最小压力,其增长速率比在0.5~0.7 mm间隙范围内快。如图12(c)所示,同一间隙下,承载力随转速增大而增大,高转速(大于500 r/min)下的承载力增长速率比低转速(小于500 r/min)下快。间隙不同时,相邻2条曲线的承载力之差随转速增大而逐渐增大。相同转速下,承载力随着间隙的增大而减小;在0.3~0.5 mm间隙范围内的承载力,其减小速率比在0.5~0.6 mm间隙范围内快。如图12(d)所示,相同间隙条件下,摩擦因数随转速增大而增大,且整体增长速率较快。相同转速下,摩擦因数随间隙增大而减小,当间隙较小时(间隙小于0.5 mm),摩擦因数减小的速率较快,间隙较大时(间隙大于0.5 mm),摩擦因数减小的速率则十分缓慢。此外,随着转速的升高,达到饱和的正、负压承载区,其动压效应向邻侧转移,这也是压力随转速升高而增大的原因。
3.4 偏心率对润滑性能的影响规律
选取典型间隙0.4~0.8 mm,典型转速600 r/min,研究偏心率分别为0.2、0.4、0.6、0.8和0.9时压力、承载力和摩擦因数的变化规律,如图13所示。
从图13(a)中可看出,相同间隙情况下,最大压力随偏心增大而增大,偏心率为0.2、0.4、0.6时的压力增加速率远没有偏心率为0.8、0.9时快。同一偏心率下,最大压力随间隙增大而减小。间隙为0.4、0.5和0.6 mm时的最大压力减小幅度大于间隙为0.7和0.8 mm时。如图13(b)所示,相同间隙条件下,最小压力随偏心增大而减小;并且偏心不同,最小压力减小速率也不同。偏心率较小时(小于 0.6),最小压力随着偏心率的增大而缓慢减小,其压差梯度几乎保持不变,二者呈线性关系。偏心率较大时(大于0.6),最小压力随着偏心率的增大而急剧减小,其压差梯度呈现增大的态势,二者呈非线性关系。偏心率相同时,随着间隙增大,最小压力也在增大,相邻2条曲线的压力之差随间隙增大而减小。如图13(c)所示,在相同间隙条件下,承载力随偏心率增大而增大,并且偏心率不同,承载力增大速率也不同。小偏心率下(偏心率小于0.6)的承载力增长速率远低于大偏心率下(偏心率大于 0.6)。相同偏心率下,承载力随间隙增大而减小,相邻2条曲线间的承载力之差也随间隙的增大而增大。如图13(d)所示,相同间隙下,摩擦因数随着偏心率的增大而增大,并且由于偏心率的不同,摩擦因数增大速率与承载力相似,在此不再赘述。同一偏心率下,相邻2条曲线间的摩擦因数之差也与上述承载力之差相似。
根据曲线中云图所示,随着偏心率的增大,动压效应从无到有、从弱到强、从小到大。同一偏心率下,随着间隙的增大动压效应也在增强。综上可知,在转速为600 r/min时,大偏心率、大间隙对动压效应的形成起到积极作用。
3.5 间隙对润滑性能的影响规律
选取典型偏心率0.8,在转速600~1 000 r/min下,研究承间隙分别为0.3、0.4、0.5、0.6、0.7 mm 时压力、承载力和摩擦因数的变化规律,如图14所示。
如图14(a)所示,相同转速条件下,最大压力随间隙增大而减小。小间隙(间隙小于0.5 mm)下的最大压力减小速率大于大间隙(间隙大于0.5 mm)下。相同间隙下,转速增大,最大压力随之增大,相邻曲线间的压力差随间隙增大而逐渐减小。如图14(b)所示,转速相同时,最小压力随间隙增大而增大,间隙小于0.5 mm的压力增长速率比间隙大于0.5 mm的快。不同转速情况下,压力与间隙之间的规律与前述规律相似。相同间隙下,转速增大而最小压力减小,相邻2条曲线间的压力差随间隙的增大而减小。如图14(c)所示,同一转速条件下,承载力随间隙增大而减小。当间隙较小时(间隙小于0.5 mm),承载力减小速率较快,间隙较大时(间隙大于0.5 mm),承载力以缓慢趋势减小;同一间隙下,承载力随着转速的增大而增大,相邻曲线间的承载力之差随间隙增大而减小。如图14(d)所示,同一转速下摩擦因数随间隙增大而减小,整体减小速率较平缓。同一间隙下,摩擦因数随转速的增大而增大,相邻曲线间的摩擦因数之差几乎保持不变。
此外,间隙为0.3 mm时动压效应已经形成,随着间隙逐渐增大,正、负压承载区向周围区域转移部分压力,并且间隙越大转移趋势越强。
4 结论及展望
针对新一代核电站二回路主循环系统中的铅铋轴承存在的动力学特性和润滑机制尚不清晰等问题,研究了间隙、转速、偏心率和有无环形导流槽等因素对铅铋轴承流体动力学特性的影响。得到如下结论:
(1)环形导流槽对承载力和摩擦因数的影响远小于无环形导流槽。
(2)最大压力随着转速、偏心率的增大而增大,随着间隙的增大而减小。
(3)最小压力随着转速、偏心率的增大而减小,随着间隙的增大而增大。
(4)相同间隙和偏心条件下,随着转速的升高,达到饱和的正、负压承载区,其动压效应向邻侧转移。
(5)相同间隙和转速条件下,随着偏心的增大,动压效应从无到有、从弱到强、从小到大。
此外,研究表明,铅铋轴承8沟槽模型摩擦虽然比6沟槽大,但其承载亦远大于6沟槽。因此,在摩擦和承载之间存在一个最优平衡范围,使得铅铋轴承达到增载减阻性能最优化,这也是下一阶段重点研究内容。文中研究成果为新一代核主泵系统铅铋轴承设计研发及国产化奠定了坚实基础。

