基于流固热耦合的浮环密封力学特性数值研究*
姜金裕 孙 丹 赵 欢 王 双 胡海涛 常 城
(1.沈阳航空航天大学航空发动机学院,辽宁省航空推进系统先进测试技术重点实验室辽宁沈阳 110136;2.中国航发四川燃气涡轮研究院 四川成都 610599)
浮环密封作为一种有效的多用途密封,广泛应用于火箭发动机、压缩机、航空发动机等机械中。浮环密封在高转速、大压差、高温情况下工作,因而要求其具有良好的泄漏特性和可靠性。浮环密封的运行状态决定了密封系统的安全性,其恶劣的工作环境会对密封的结构产生影响[1],直接影响到密封性能、寿命及稳定性。螺旋槽浮环密封的流体域很薄,微小的间隙变化都会对密封的泄漏特性及稳定性产生很大影响,因此对浮环密封力学特性的研究尤其重要。
在浮环密封的结构与数值计算研究方面,NASA在Rayleigh阶梯密封垫的基础上研究了浮环密封的材料、结构参数、跑道形状等方面对密封性能的影响[2-3];ARGHIR和MARIOT[4]通过理论与数值相结合,深入研究了结构和工况参数对泄漏量与摩擦功耗的影响;夏鹏和刘占生[5]研究了在高压条件下,浮环密封的弹性变形对密封间隙中流体激励产生的影响;杨宝锋等[6]通过修正Bulk-Flow模型和CFD准稳态法,研究得知浮环密封在大偏心率下各动力学特性系数会明显增大,而且大扰动下,各动力特性系数与扰动量之间有复杂的非线性关系;NELSON和NGUYEN[7]采用快速傅立叶变换法,得到了浮环密封的动力学特性系数;SAN ANDRES[8]、ARGHIR和FRENE[9]通过简化理论模型,研究得到了浮环密封动力学稳定性以及泄漏量的大小;邵山中[10]利用有限元模拟分析了浮环密封的应力、摩擦磨损以及泄漏量受转子跳动的影响规律;郑利胜[11]对浮环密封进行了稳态热与热-结构耦合数值分析,从而得出了浮环密封的工作状态。
在浮环变形研究方面,丁雪兴等[12]研究了高压高转速工况下浮环密封的变形量;赵芳等人[13]对浮环密封的静环做了力变形分析;扈中平[14]基于流固耦合对浮环密封的静环与动环进行了热与力变形研究;丁雪兴等[15]采用流固耦合方法研究了碳化硅、铝合金等材料浮环密封在不同工况参数下的变形;白超斌等[16]利用流固耦合的方法研究了浮环的气膜厚度和偏心率等参数对浮环支撑结构等效应力与应变的影响。
综上所述,现有文献大都基于流固耦合方法研究结构与工况参数对浮环密封泄漏量、变形与应力的影响,没有考虑温度的影响,而温度对力学特性有较大的影响。因此开展基于流固热耦合的浮环密封力学特性研究具有重要的实际意义。本文作者应用流固热耦合方法,建立了不同材料的浮环密封的流固热耦合求解模型,计算不同材料浮环密封在不同工况下的应力与变形量,并分析其影响规律。
1 浮环密封流固热耦合理论分析
1.1 流固热耦合热量传递过程
考虑浮环密封内表面上受到流场作用下的流固耦合与传热问题,该过程涉及浮环密封中流体的流动与传热、内部流体与固体界面之间的热传导以及固体自身内部的热传导,涉及到的控制方程主要包括固体的传热方程,流体的质量、动量和能量方程[17]等。流体域与固体域交界面处的边界条件由动态换热来决定而不能对其进行预先设定,所以必须联立求解各方程。图1所示为浮环密封流固热耦合计算热传递示意图。
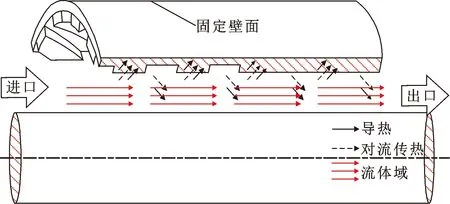
图1 浮环密封流固热耦合热传递示意
1.2 流体域控制方程
文中计算模型中流体域很薄,流场经过计算为层流,在文中流固热耦合计算工况下,流体流动满足以下方程。
连续性方程:
(1)
式中:Ux、Uy、Uz分别为x、y、z3个方向的速度分量,m/s;t为时间,s;ρ为密度,kg/m3。
引入哈密顿微分算子
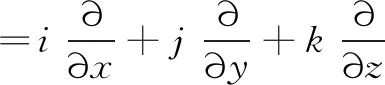
(2)
则式(1)可表示为

(3)
(4)
动量守恒方程:
该方程满足牛顿第二定律。根据这一定律可导出x、y、z3个方向的动量方程:
(5)
式中:p为流体微元体上的压力,Pa;τxx、τyx、τzx是指在分子黏性作用下,产生的作用在微单元体表面的黏性应力的分量,Pa;fx、fy、fz为3个方向的单位质量力,m/s2。
能量方程:
(6)
式中:ρ为密度;t为时间;p为压力;T、k、cp分别为流体的温度、传热系数、比定压热容;ST为流体耗散项。
1.3 固体域控制方程
浮环密封在流体作用下的响应,满足结构动力学方程,该方程[18]为
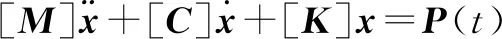
(7)
即
(8)
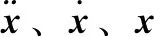
1.4 传热控制方程
由热平衡可知,在流固热耦合面处的导热热通量与对流热通量相等,即qw=qc,得到如下关系[19]:
(9)
式中:∂为对流换热系数;λ为导热系数;Ts为固体表面温度;Tf为流体表面温度。
1.5 流固热耦合控制方程
浮环密封流固热耦合交界面处应满足流体与固体的应力、位移、热流量、温度均相等[20-21]。
(10)
式中:τ为应力;d为位移;Q为热流量;Tf为流体表面温度;Ts为固体表面温度;n为交界面的法线方向,交界面上的应力需在法线方向上达到平衡。
文中计算的浮环密封变形量,是通过流固热耦合面将浮环密封流体域数值计算所得到的压力和温度,施加到浮环密封的流固热耦合表面上得到的。通过静力学结构分析模块对不同材料浮环密封进行力学特性分析,图2中给出了浮环密封力学特性结果的提取过程。

图2 浮环密封特学特性结果提取流程
文中通过建立浮环密封三维实体模型,实现浮环密封与封严气体的流固热耦合分析[22]。如图3所示,Tn时刻循环开始,取Tn+1时刻的流场分布和浮环密封变形的位移作为初始条件,在流体域计算结果收敛后,通过网格插值将得出的流场分布情况传递到流固热耦合面上,并作为密封耦合面的边界条件进行计算并得到浮环密封动力响应,直至流体域与固体域计算都达到收敛时,则完成一次耦合迭代计算。
2 浮环密封流固热耦合求解模型
2.1 几何模型
文中建立了浮环密封流固热耦合数值求解模型,该模型在浮环内表面周向均匀布置16个相同的螺旋槽结构。浮环密封几何参数如表1所示。浮环密封结构如图4所示。
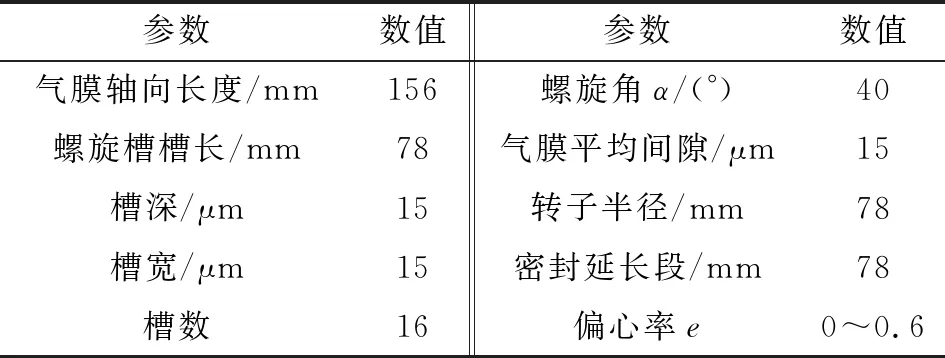
表1 浮环密封几何参数

图4 浮环密封结构
文中浮环密封材料采用石墨烯、石墨、铝合金、碳化硅4种不同材料。这些材料在航空领域有很大的应用价值,特别是石墨烯,应用前景广阔。浮环密封材料性能如表2所示。
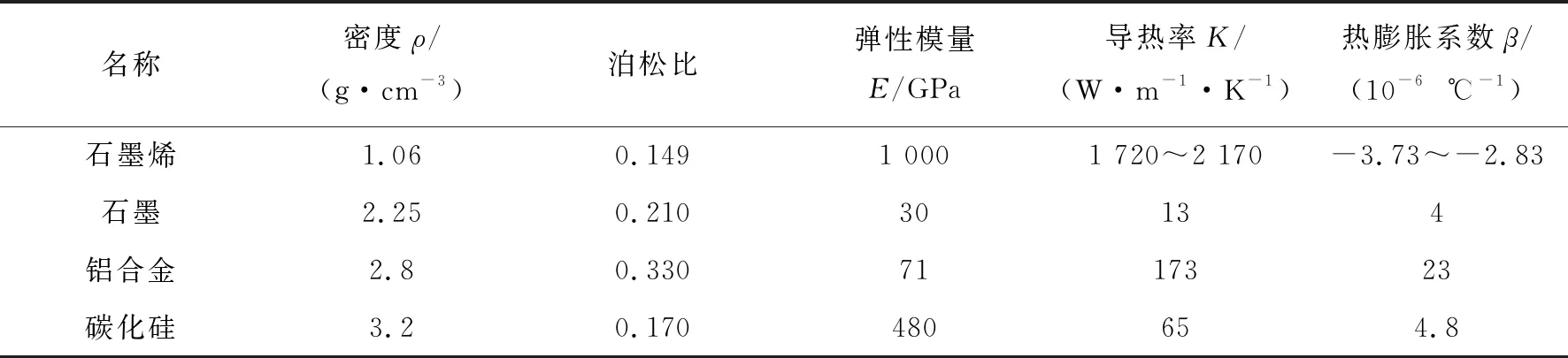
表2 密封材料机械性能
2.2 网格划分
文中对浮环密封流固模型采用六面体网格划分方式。图5所示为浮环密封流固模型网格划分结果。选择多个不同的模型网格数量进行网格无关性验证,不同数量网格的模型泄漏量计算结果如图6所示;综合考虑求解精度及计算时间,气膜周向尺寸设置为0.2 mm,气膜径向节点数设置为4,螺旋槽径向节点数设置为6;螺旋线的网格尺寸设置为0.3 mm,螺旋槽周向网格尺寸设置为0.3 mm;确定流体域网格数目为220万。确定固体周向尺寸设置为0.4 mm,固体径向节点数设置为6,螺旋槽径向节点数设置为6,螺旋线的网格尺寸设置为0.5 mm;确定固体域网格数目为100万。最后,模型网格数量选取为320万。

图5 浮环密封流固耦合网格划分

图6 网格无关性验证
2.3 边界条件及求解方法
表3给出了文中求解模型的边界条件。流体域进口设置为总压,出口设置为静压1 MPa,进出口压比为3~7,温度为300~500 K;给定转子转速,工质选用理想空气,采用层流模型,近壁面区域采用改进壁面函数法,固定壁面为光滑、绝热、无滑移边界。当连续、动量、能量方程残差下降到10-6,认为计算收敛。表3给出了浮环密封的工况参数。图7给出了浮环密封流固热耦合边界。
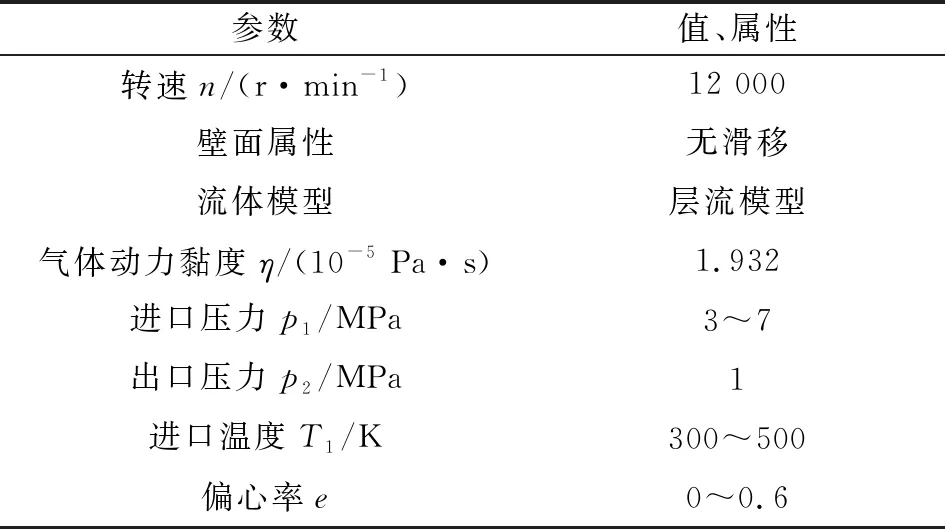
表3 密封模型工况参数
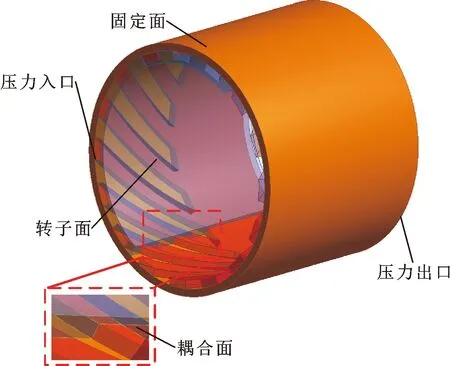
图7 流固热耦合边界条件
文中浮环密封的材料分别采用石墨烯、石墨、铝合金以及碳化硅4种材料,浮环密封结构的固定端采用固定约束,将浮环密封内表面设置为流固热耦合面。将流场计算收敛后的温度和气流力结果导入到流固热耦合面上,实现流固热耦合的数据传递。
2.4 准确性验证
为了验证文中计算方法准确性,基于俞树荣等[22]的螺旋槽浮环密封模型,应用文中的数值方法对其的泄漏量开展计算并分析,并将文中数值计算结果与文献实验和数值计算结果进行对比验证。经计算得出在0.3~0.6 MPa压差下文中与文献数值仿真的泄漏量平均偏差为7.6%,与文献实验结果对比,泄漏量平均偏差为16.3%,如图8所示。文中数值计算的泄漏量与文献值变化趋势吻合较好,验证了文中数值计算方法的可靠性。
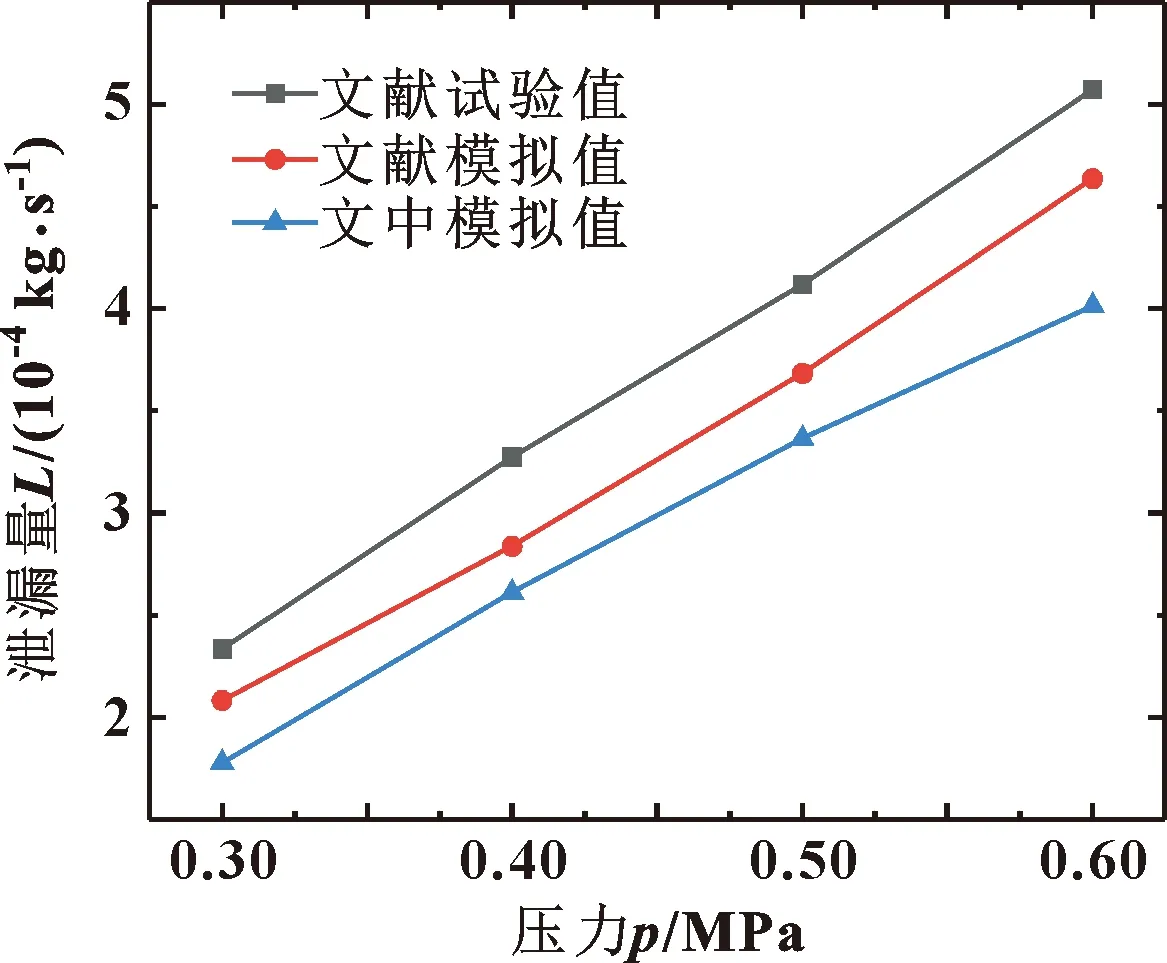
图8 文中计算结果与文献[22]结果比较
3 数值求解结果及分析
3.1 密封流场特性分析
3.1.1 密封流场压力分布分析
图9给出了进口压力为5 MPa,出口压力为1 MPa,转速为12 000 r/min,温度为300 K时,不同偏心率时浮环密封流场压力云图。可以看出,同心时流场压力沿周向呈阶梯式降低的变化规律,这是由于浮环内侧的槽与槽之间存在台阶,会使气流产生节流效应,从而使压力降低,其周向压力分布均匀。从图中还可以看出,存在偏心时,在较薄流体域一侧形成了局部高压区,较厚一侧的压力无明显变化,这是由于当浮环与转子偏心布置时,二者之间存在楔形间隙,气流经过这种结构会产生动压效应,且随着偏心率的增加这种效果更加明显。
为能更直观地看出浮环偏心对流场压力的影响,选取偏心位置即流体域气膜最薄处以及其气膜最厚处的轴向压力,选取位置如图10所示。图11给出了在不同偏心率的情况下,流体域薄厚两侧沿轴向压力变化曲线。可以看出,同心时两侧的压力保持一致,而随着偏心率的增加,两侧的压力差逐渐增大;同心时,最高压力为5 MPa,当偏心率为0.6时,局部最高压力为5.63 MPa,比同心的最高压力提高了12.6%,因此浮环密封有较强的自同心能力。

图10 轴向压力选取位置示意

图11 不同偏心率时流场压力随轴向长度变化
3.1.2 密封流场温度分布分析
图12给出了进口压力为5 MPa,出口压力为1 MPa,转速为12 000 r/min,进口温度为300 K时,不同偏心率时浮环密封流场温度分布云图。可以看出,同心时,从入口到出口温度逐级递增,到出口时温度达到最大值;偏心时,在流体域较薄一侧会出现局部高温区,且随偏心率增加,局部高温区的温度越大,且高温区都出现在出口位置。当偏心率为0.6时,局部最高温度为952 K,较同心的396 K高出了556 K,升高了140%,可以得出偏心对流场温度有很大的影响。

图12 不同偏心率时浮环密封流场温度分布云图
3.1.3 泄漏特性分析
图13给出了出口压力为1 MPa,转速为12 000 r/min,进口温度为300 K时,不同偏心率时,浮环密封泄漏量随进口压力的变化规律。可以看出,泄漏量随着进口压力的升高而逐渐增加,且上升的趋势越来越大;当进口压力相同时,泄漏量随着偏心率的增加而增加,而且随着进口压力的增加,不同偏心率之间泄漏量的差值也在逐渐增大,因此偏心率对浮环密封的泄漏特性有较大的影响,而浮环密封较好的自同心能力可以调节浮环密封在工作中偏心率较大的问题,从而达到降低泄漏量的目的。
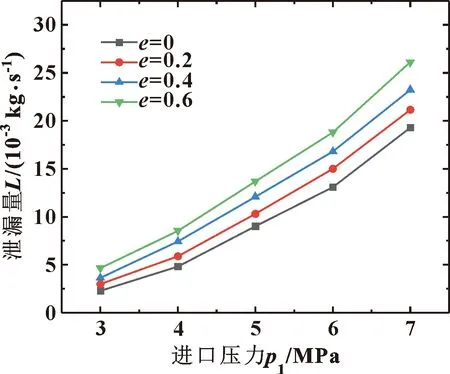
图13 不同偏心率时泄漏量随进口压力的变化
3.2 浮环密封结构力学特性分析
3.2.1 浮环密封结构变形分析
图14给出了进口压力为5 MPa,温度为300 K时,采用石墨烯、石墨、铝合金与碳化硅4种材料为浮环密封材料时的变形量。可以看出,4种材料的浮环密封的变形量大小分布基本一致,其中后半段的变形量大,且最大变形量主要集中在出口位置,进口螺旋槽位置的变形量相对较小;4种材料的浮环密封变形量中石墨烯最小,变形量为0.5 μm,铝合金最大,变形量为9 μm。图15给出了浮环密封在进口温度为500 K,转速为12 000 r/min,出口压力为1 MPa时,密封中流体域的平均温度随进口压力的变化规律。可以看出,流体域的平均温度随着进口压力的增加而降低。
图16给出了浮环密封在出口压力为1 MPa,转速为12 000 r/min,进口温度为300 K时,进口压力对不同材料浮环密封变形量的影响。可以看出,石墨烯、石墨、铝合金、碳化硅浮环密封件的变形量均随着进口压力的增加而降低。结合图15可知,温度对浮环密封变形量的影响大于压力的影响,进口压力为3 MPa时,流体域温度最高,所以4种材料浮环密封件的变形量在3 MPa时最大,在7 MPa时温度最低,变形量最小。在进口压力相同时,石墨烯的变形量最小,然后依次为碳化硅、石墨、铝合金浮环密封件;其中石墨、石墨烯与碳化硅的变形量随着进口压力的升高变化不大,而铝合金浮环密封件的变化很大。在进口压力为3 MPa时,流体域平均温度为141 K,温度对铝合金材料密封变形量的影响较大,相较于同温度下的石墨烯,铝合金的密封变形量比石墨烯材料高出6.82倍。

图15 进口压力对流体域温度的影响

图16 进口压力对4种浮环密封件变形量的影响
图17给出了温度对不同材料浮环密封变形量的影响。可以看出石墨烯、石墨、铝合金和碳化硅4种材料浮环密封变形量随温度的升高而增大,其中铝合金浮环密封的变形对温度更加敏感,另外3种材料浮环密封的变形量没有随温度大幅度增加。当温度为300 K时,铝合金的变形量是石墨烯的3.7倍,当温度为500 K时,铝合金的变形量是石墨烯的5.7倍。

图17 温度对4种浮环密封件变形量的影响
3.2.2 密封结构应力分析
图18给出了进口压力为5 MPa,进口温度为300 K,转速为12 000 r/min时,采用不同材料浮环密封结构的应力分布。可以看出,等效应力的最大值主要分布在浮环密封的后半段,靠近出口的位置。等效应力的最小值,主要分布在浮环密封靠近进口位置的螺旋槽内。另外,4种材浮环密封的平均等效应力均小于屈服应力,故均可以正常工作,不会产生断裂。
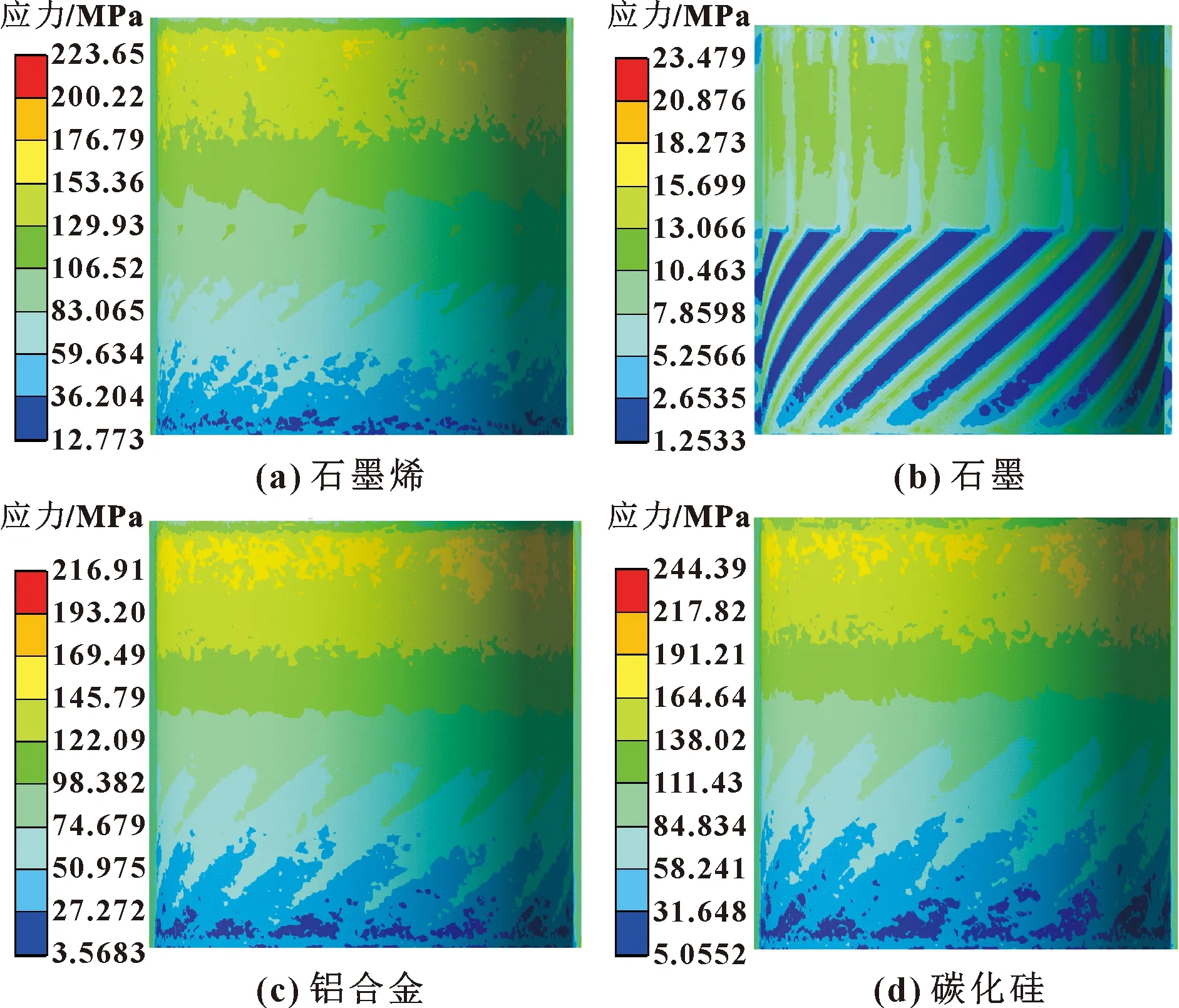
图18 不同材料浮环密封结构的应力分布
图19给出了不同材料的浮环密封平均等效应力随进口压力的变化曲线。可以看出,随着进口压力的增加,4种材料浮环密封的平均等效应力大小变化规律基本一致,呈逐渐减低趋势,其中石墨烯、铝合金与碳化硅浮环密封应力随压力的变化较为明显,石墨材料浮环密封应力随进口压力的增加变化不大。温度会对材料的弹性模量、导热系数、热膨胀系数等参数产生较大的影响,使得该4种材料的应力对温度十分敏感。因此进口压力对温度产生影响,温度随着进口压力的增加而降低,平均等效应力也随着进口压力的增加而降低。
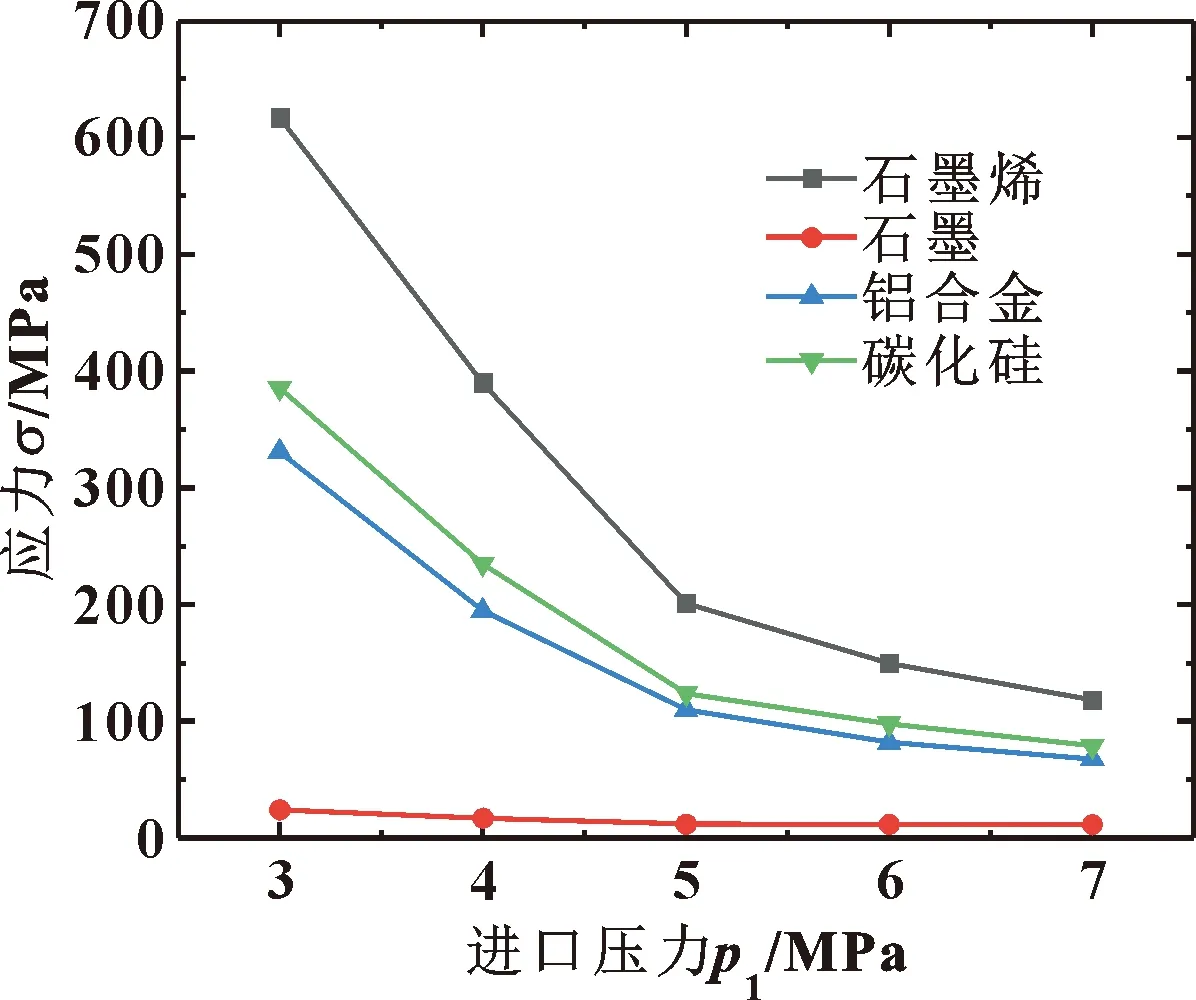
图19 进口压力对4种浮环密封件应力的影响
图20给出了不同材料浮环密封平均等效应力随温度的变化曲线。可以看出,4种材料浮环密封的平均等效应力随温度的增加而增大;石墨烯材料浮环密封的等效平均应力受温度影响较为明显,温度为500 K时,应力较300 K时升高了727%;石墨材料浮环密封件受温度影响较小,500 K温度较300 K时应力提升了410%。

图20 温度对4种浮环密封件应力的影响
4 结论
(1)浮环密封在偏心时,由于楔形间隙的存在,气流经过这种结构产生流体动压效应,在较薄的流体域一侧形成局部高压区,较厚的一侧压力无明显变化,温度分布与之相同。
(2)浮环密封的泄漏量随压比的增加而增大,随偏心率的增加而增大。
(3)浮环密封随进口压力的增加,流体域温度降低,变形量随着降低,其中温度对密封变形量的影响超过压力对其的影响。
(4)浮环密封随进口温度的增加,平均等效应力与平均变相量均增加,且同温度下铝合金浮环密封的变形量最大,石墨烯的最小;石墨烯浮环密封的应力最大,石墨的最小。

