干式摩擦元件的热弹不稳定性分析*

郭 超 张 昱 杨 凯

(1.中国航空发动机研究院 北京 101304；2.北京航空航天大学机械工程及自动化学院 北京 100191；3.北京卫星制造厂 北京 100094)

摩擦元件的热弹不稳定性是指由于其制造、安装、结构、控制等方面的不足，制动器内部的物理场存在一定的初始非均匀性，当制动速度超过临界值时，系统将出现热弹性不稳定(Thermoelastic Instability)状态，简称TEI[1]。制动器出现热弹性不稳定(TEI)现象，加速了材料的磨损及热疲劳破坏，另外还引入了“热颤振”(Hot Judder)导致系统产生摩擦振动与噪声的可能性加大，因此，TEI是影响制动器稳定性能的关键因素之一，必须深入研究。

PEI等[2]分析了摩擦系统中摩擦热导致的热机械失稳机制，提出一种热边界控制方法，并研究了转盘在气流下的气动弹性不稳定性问题。ABDULLAH等[3]用Perturbation方法研究了2个摩擦面接触的稳定性问题。对于热弹性失稳的研究，需要分析临界转速，超过临界转速是热弹性失稳的主要原因。TANG等[4]采用有限元法建立了离合器热弹性不稳定性的瞬态模型。马彪、于亮等人[5- 6]建立离合器接合过程的二维理论模型，分别求解了采用不同摩擦材料的离合器发生TEI时的临界速度等。SHPENEV[7]通过有限差分方法建模分析各向异性圆盘样品在非定常摩擦下引发热弹性失稳的问题。HAN和GU[8]采用数值方法研究TEI问题，将求解临界速度问题转化为求解系统矩阵特征值问题。YU等[9]首次采用扰动法研究了系统的TEI问题。WALIA等[10]研究发现系统相对滑动速度较高时，扰动会向表层集中。扰动的来源往往是多方面的，与系统结构、温度场、磨损量、压力分布以及应力状态有关。

抛开系统状态说系统稳定性问题是不全面的，WANG等[11-13]从定性和定量2个方面对制动器工作过程中接触摩擦生热、瞬态温度场、对偶件的变形和应力及接触压力分布等制动器热弹性耦合分析的基本问题，进行了较为广泛的研究。

本文作者在上述研究的基础上，进一步探讨干式摩擦元件热弹性失稳的原因，将理论分析和有限元仿真相结合，对干式摩擦元件进行热弹不稳定分析。

1 干式摩擦元件热弹不稳定分析模型

当两个相互接触的物体产生相对滑动时，由于表面不规则粗糙，真实接触面积是由名义接触区域内许多微凸体接触产生的。因此界面上压力分布本质上是不均匀的，这种微观的不均匀是导致系统不稳定性的根本原因。相对摩擦所产生的热将引起接触体的热弹性变形，进而改变接触面之间的压力分布。反之，接触面间压力分布不均匀，又使局部产热更加不均匀，当系统能量输入超过其能量耗散时，该过程将不可逆转地恶化下去，使得微观尺度下的不均匀性会随着温度累计形成宏观的局部高温点。因此，对于给定的摩擦因数，将存在着某个滑动速度，当高于此数值时，系统将变得不稳定，即产生TEI现象[14]。

所以对摩擦元件热弹性不稳定性问题的研究，主要集中在求解摩擦系统进入热弹性不稳定状态的临界速度，分析摩擦元件在热弹性不稳定状态时摩擦表面的温度场分布，热点分布规律，系统参数对热弹性不稳定性的影响等方面。在理论方面对于干式摩擦系统的TEI问题研究一般采用扰动法，在Barber和Burton模型的基础上，改进模型参数，利用伽辽金法[15]，分别建立摩擦副系统二维有限元模型，通过求解TEI矩阵的特征值得到摩擦副在不同滑摩速度下的扰动增长系数，并确定TEI临界速度。

首先建立摩擦副热二维TEI有限元模型(如图1所示)，通过有限元研究结果与解析法研究结果的对比，证明有限元模型计算结果的准确性。材料1、2分别表示摩擦材料与对偶材料，面积分别为A1、A2，边界分别为C1、C2。2种材料接触边界为C3，材料1以速度v、沿X轴正方向运动。

图1 2D有限元TEI模型示意

首先假设摩擦副内的温度场、应力场、热流密度、热弹性变形等物理场的扰动均可以表示成余弦形式，扰动的幅值随时间呈指数变化，在笛卡尔坐标系下可以表示为

R{F(y)exp(bt+iλx)}

(1)

同样的温度扰动为

R{T(y)exp(bt+iλx)}

(2)

式中：R表示公式取实部；F(y)表示应力；T(y)表示温度；b表示扰动增长系数；λ表示扰动空间频率，i=-1的开方。

考虑对流，那么热传导方程存在对流项，表示成：

(3)

式中：K为材料的导热系数；ρ为密度；cp表示比热容。

将扰动代入热传导方程可得：

(4)

然后对表面进行积分，表面考虑权函数w(y)可得：

(5)

利用分步积分法，

(6)

将其化简得到：

(7)

热流密度对温度场的扰动可以表示成：

(8)

将其代入热传导方程中，得：

(9)

将其离散化，引入有限元形函数，

(10)

式中：Nj表示材料的节点数；Tm表示第m个节点上的温度扰动值；Wm(y)表示形函数。

在伽辽金方法中，权函数与形函数相等，所以可以得到：

(11)

式中：Wm和Wn分别表示形函数和权函数；WmWn表示一个Nj×Nj的矩阵，表示成矩阵为WmWn=WWT。至此文中就建立了基于扰动关系的二维有限元热传导模型。

形函数可以表示为

Wm=[W1，…，WNj]T

(12)

以上方程可以改为矩阵形式：

(K+G+bL)T+Q=0

(13)

式中：矩阵K为N维传导矩阵；G为N维系数矩阵；L为N维质量矩阵；T表示温度向量；Q为热流向量。

各矩阵和向量的表达式为

(14)

G=∬Aj(Kjλ2+ρjcpjiλvj)WWTdAj

(15)

L=∬Aj(ρjcpj)WWTdAj

(16)

(17)

综上，建立干式制动器摩擦副系统热弹不稳定分析模型。模型的求解，关键是确定过渡矩阵H，它是一个Nc×N矩阵。利用有限元分析软件ABAQUS，计算各节点温度场和接触压力，从而推导过渡矩阵。

2 干式摩擦元件热弹不稳定分析结果

系统矩阵与特征值解法，根据边界特征可知，2个表面之间的热流只存在于接触表面。所以接触表面节点数为Nc时，如果另一个方向也是Nc，则Nc=N，否则Nc=N1+N2-N。那么此时一定存在矩阵S满足：

Q=SQc

(18)

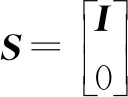
(19)

式中：Qc、I分别为接触热流密度Nc维向量、Nc×Nc单位矩阵；矩阵S为N×Nc矩阵。

根据热流计算公式：

q=μvp

(20)

式中：p为压力；v是相对滑动速度；μ为摩擦因数。

将式(20)写成矩阵代入方程(18)中可得：

Q=SQc=μvSHT

(21)

代入方程(13)中可得：

(K+G+bL+μvSH)T=0

(22)

构造矩阵U，使得：

UT=bT

(23)

则矩阵U的特征值，就是扰动增长系数b。从式(22)中可以看到，扰动增长与摩擦因数和滑动速度相关。当扰动增长系数恰好为0时，对应的摩擦副的相对滑动速度v即为热弹不稳定的临界速度。根据制动器摩擦副热固耦合有限元仿真计算结果，导出接触表面的温度矩阵T和压力矩阵pc，所以过渡矩阵可以写成如下形式：

pc=HT

(24)

摩擦副部分的热固耦合有限元计算结果如图2所示，其中图2(a)所示为一对摩擦副(对偶片和摩擦片各一组)相互贴合下的正应力分布结果；图2(b)所示为温度场分布；图2(c)所示为应力场分布。仿真工况如表1所示。

图2 摩擦副热固耦合有限元分析结果

表1 仿真工况

根据图3所示的有限元的计算结果，输出二维接触表面的温度和压力矩阵。文中构造了一个接触表面15×15的过渡矩阵，如表2所示。按照矢量关系提取摩擦副的压力与温度云图中的数据，得到每一条路径上的值，其结果如图4所示。

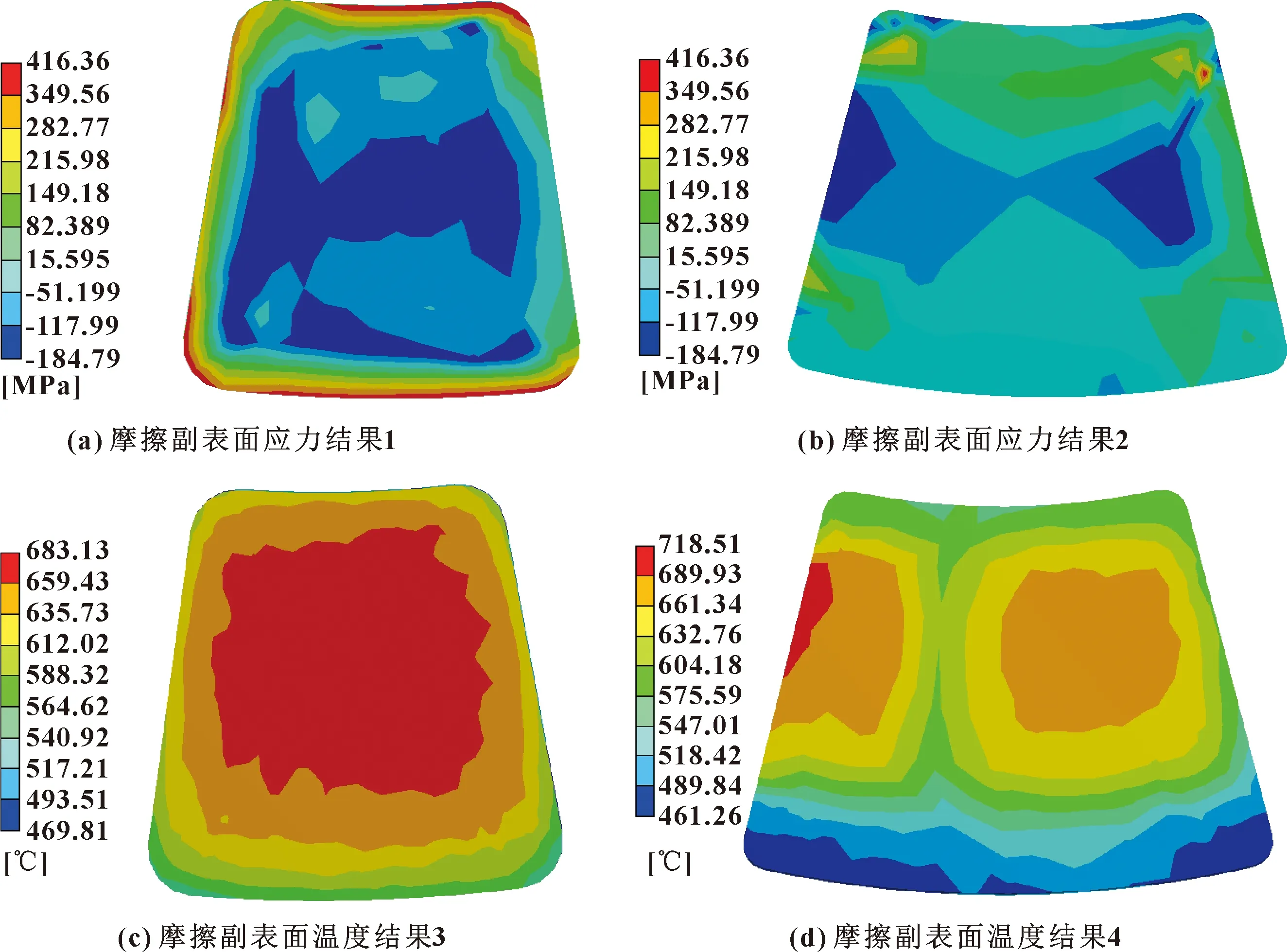
图3 不同阶段摩擦副表面应力与温度

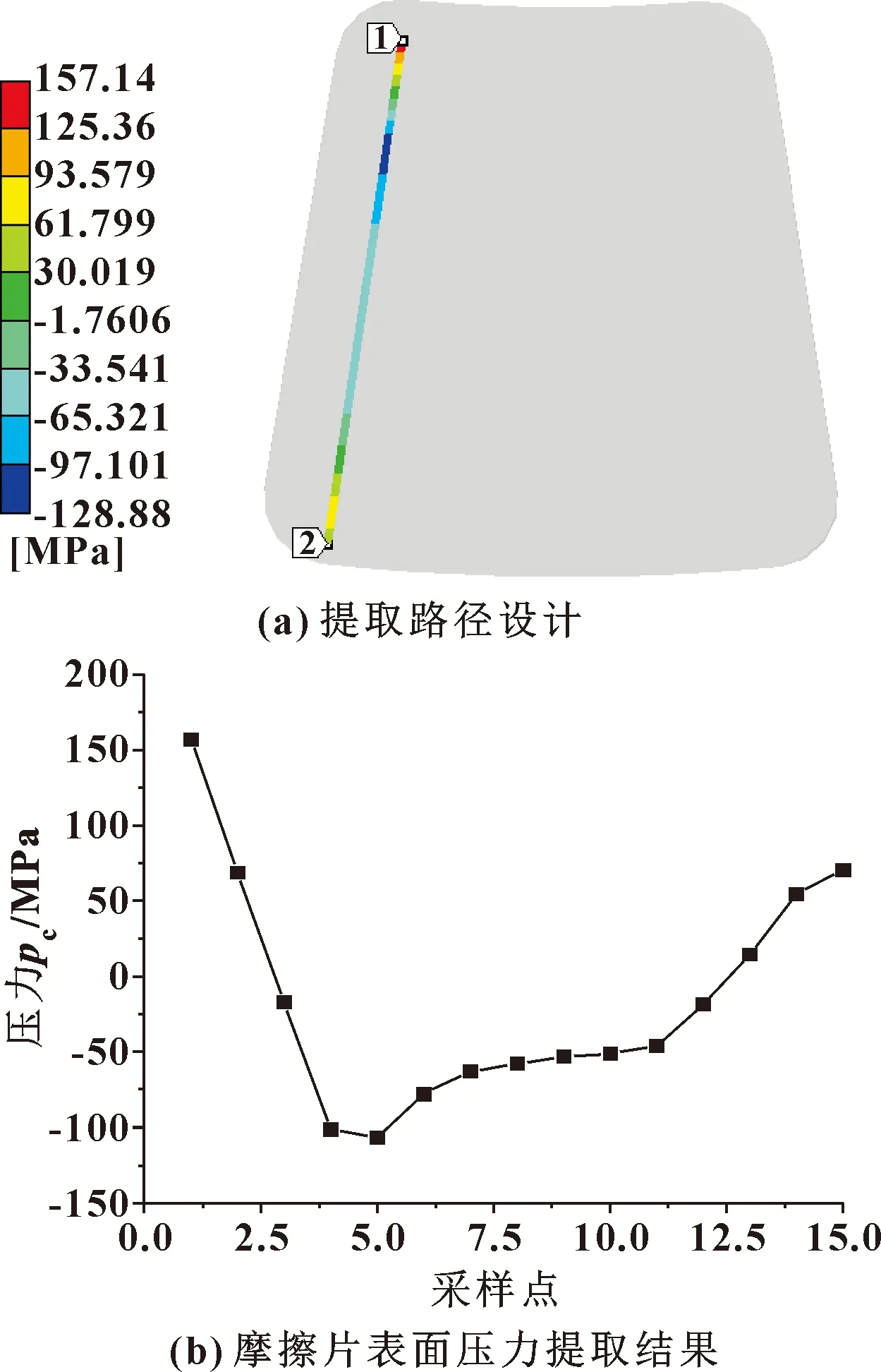
图4 摩擦副表面接触压力提取

提取表面节点沿自定义向量方向的取值，然后根据节点的取值结果，计算过渡矩阵。根据温度场分布结果计算出来的过渡矩阵如表2所示。

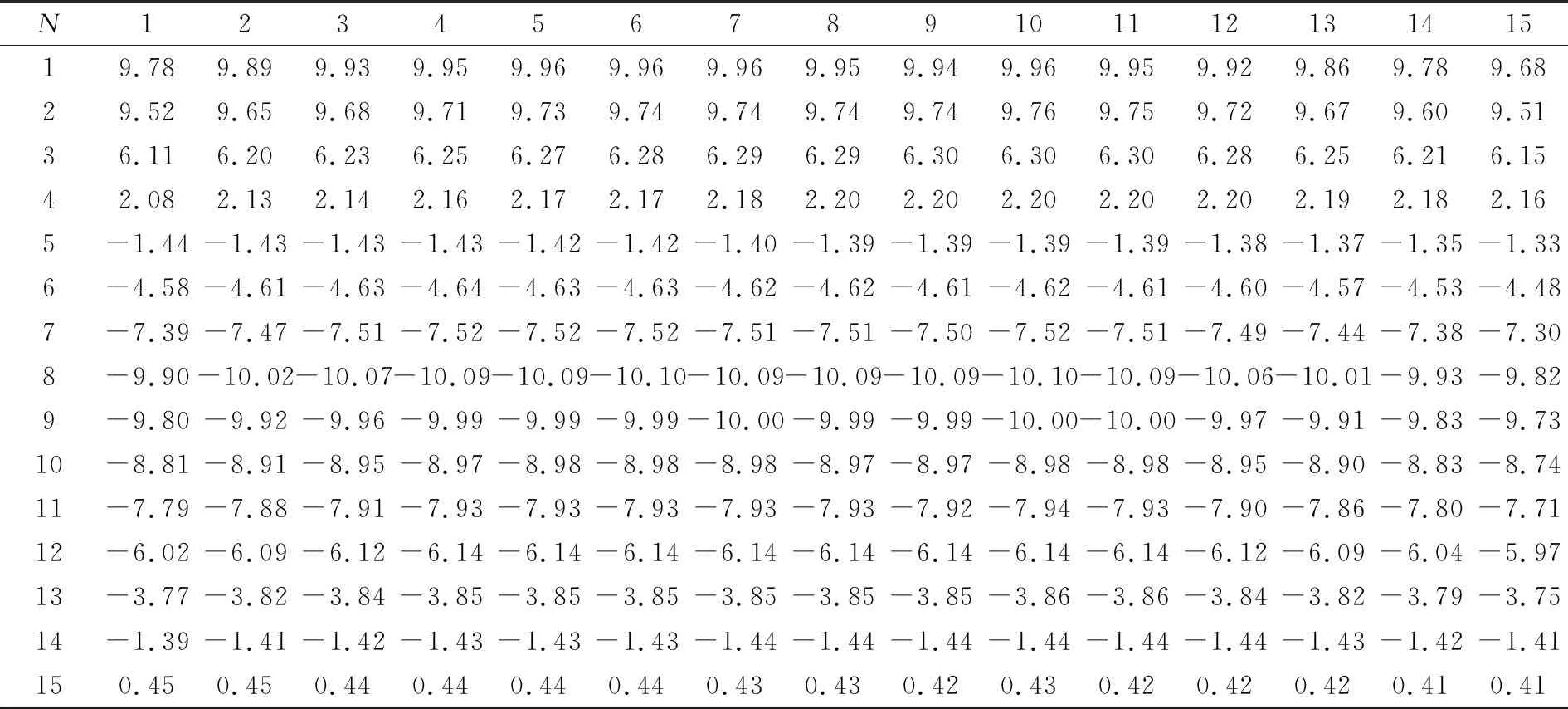
表2 过渡矩阵(×105)

将过渡矩阵代入式(22)中计算获取临界速度的值，其计算结果如图5所示。

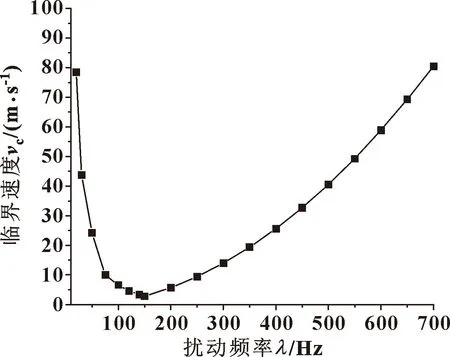
图5 临界速度典型曲线

临界速度先减小，后增大。在临界速度产生极小值之后，随着扰动频率的增加，临界速度是增大的，当扰动减小时系统的临界速度也会增大。当没有扰动时，理论上就不会产生系统失稳，那么临界速度理论上是无限大。也就是说无论转速多大，都不会超过临界速度，系统也就不会产生失稳。但是这在实际当中是不可能的，因为扰动必然存在。

针对典型工况，研究温度造成热应力、压力变化等对临界速度的影响。由于系统的输入就是由温度-压力计算获得的过渡矩阵，所以温度对于热应力的影响会通过压力矩阵传递到过渡矩阵H上。根据摩擦元件的常用工作状态，文中制定了6种典型工况参数(如表3所示)。这6种典型工况涵盖了制动器工作过程的大部分的运作状态。

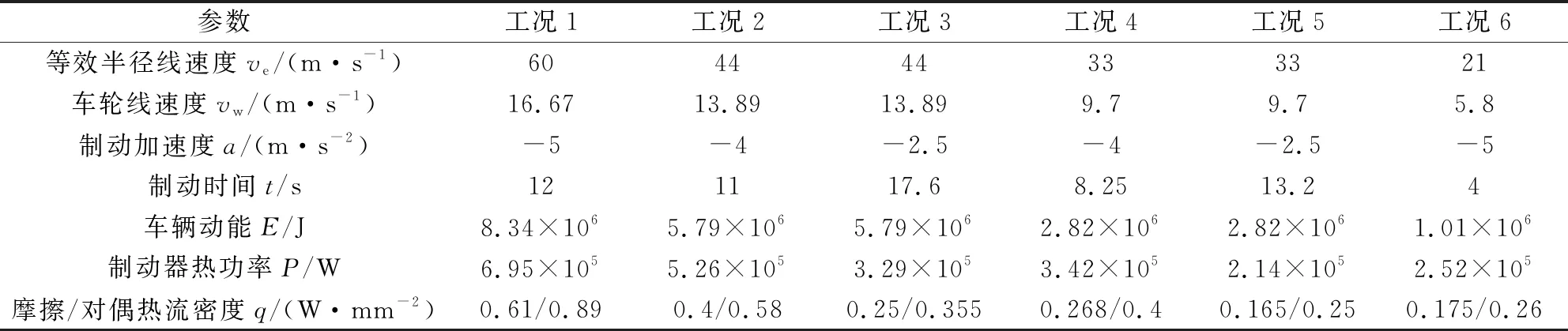
表3 6种典型工况的参数

根据热固耦合的有限元计算结果，结合6种工况获得了不同工况下的临界速度曲线，如图6所示。可以看到，并不是热流密度越高的工况造成系统失稳的可能越大。在散热条件一定的情况下，热流密度越大会造成制动器热功率越大，那么在制动器使用过程中产生的温度一般也越高。从图中可以看到工况1和工况5的最小临界速度较大，但是工况1的温度最高，工况5的温度最低(如图7所示)，这说明临界速度跟摩擦片整体的温度高低没有必然关系。6种工况中，工况6更容易产生系统失稳，这是因为工况6的制动时间更短，热量的集中释放比较明显，造成了较为明显的局部温差。

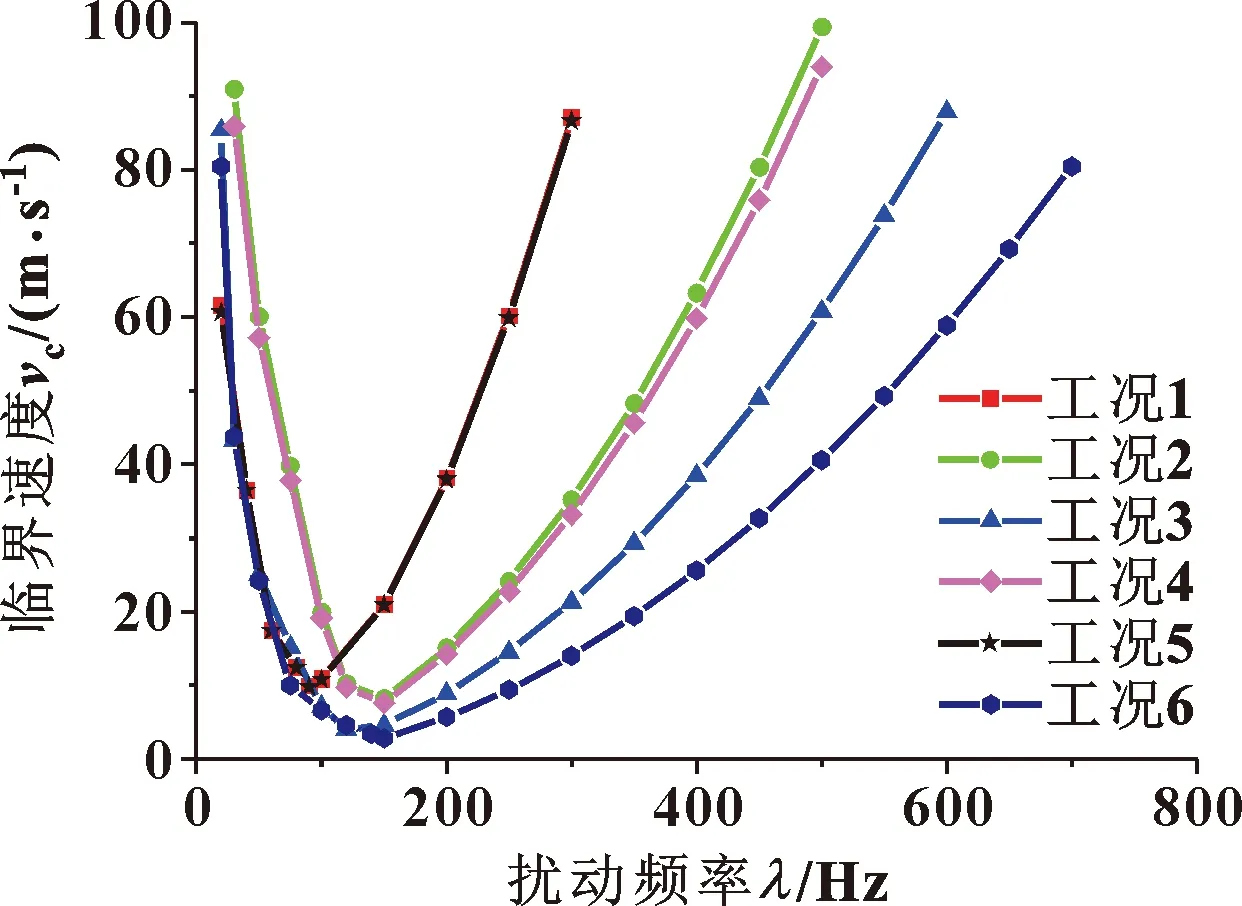
图6 不同工况下临界速度变化

图7显示了6种工况下摩擦副表面温度分布曲线和局部温度的差异。图7(a)所示为6种工况的最高与最低温度曲线，可见工况1的温度最高，工况5和工况6的温度较低。

图7(b)所示为不同工况下的摩擦片温度差，左侧的纵坐标代表绝对温差，右侧的纵坐标代表相对温差，相对温差为绝对温差与最高温度的比值。可见工况6的绝对温差和相对温差都比较大，工况2和工况4相对温差高于工况1和工况5，这与临界速度结果一致。这进一步说明了临界速度跟摩擦片整体的温度高低没有必然关系，而是与局部温差尤其是相对温差相关。因此，引起失稳的重要原因之一是局部温差，因为局部温差增大了摩擦片热弹性变形，所以系统也更加容易失稳。

图7 不同工况下摩擦片表面温度分布曲线和表面温差

3 结论

提出一种理论和仿真相结合的计算方法，可以将系统扰动因素和系统结构因素相统一，计算结果可以直接用来指导摩擦片热弹性失稳的优化设计。主要结论如下：

(1)扰动频率通过临界转速影响系统失稳，造成系统失稳的临界速度存在一个极小值点，在该点系统最容易产生失稳，高频扰动和低频扰动对系统失稳的影响较小。

(2)摩擦副局部热应力过大是造成系统失稳的主要原因，摩擦副整体温度的高低与系统失稳之间不存在必然的联系。

(3)摩擦片结构对系统失稳也有明显影响，对于文中所研究的摩擦片结构，其在通常摩擦片的线速度范围内(一般不超过50 m/s)，容易引起系统失稳的扰动频率区间为50～550 Hz。可以通过改变设计工况，或者改变摩擦片结构的方法进行调整，以避免系统失稳。