磨屑对润滑油摩擦性能的影响*

林国斌 潘 伶 郭锦阳

(福州大学机械工程及自动化学院，福州市摩擦与润滑行业技术创新中心 福建福州 350108)

在机械生产中，常会出现高速、载荷冲击、工作温度变化范围宽等工况，机械零件相对运动表面不可避免地会发生摩擦磨损，进而产生大量微小磨屑。采用润滑剂分离摩擦表面是降低摩擦磨损的有效方法之一[1-3]。其中，部分磨屑会随着废油排出，但仍有磨屑会残留在润滑油中[4-5]。磨屑作为润滑油中的杂质，一方面会进入零件接触润滑区，加剧零件的磨损；另一方面磨屑的存在会改变润滑油的摩擦学性能，无法保证设备的运行精度[1-2，6]。

在精密机械中，由于关键零部件(如轴承、齿轮)长期处于服役状态，并且承受较高的载荷，易出现乏油工况，此时润滑体系中的磨屑会随着流体流动直接与壁面发生接触[7-8]，导致机械系统的传递效率下降，缩减使用寿命[9]。沈明学等[10]通过试验指出在同粒径下角形磨屑比圆形磨屑磨损程度更大，易形成嵌入坑式表面形貌。DONG等[11]对比分析了在含砂和纯水润滑条件下的磨损行为，表明磨损量和表面粗糙度随着滑动速度、载荷和砂砾浓度的增加而增加。

尽管磨屑对润滑体系的影响受到了众多关注，但是当润滑薄膜进入纳米量级时，此时宏观上的流体力学规律不再适用，并且实物试验也无法实时观察到磨屑在润滑油中的动态行为，如磨屑吸附于壁面、团聚现象和沉积等过程[12-14]。分子动力学(Molecular Dynamics，MD)方法通过计算牛顿运动方程得到体系原子在任意时刻下的演变过程，已经广泛应用于纳米尺度下研究材料的力学响应过程[15-17]。本文作者采用摩擦学试验和分子动力学模拟结合的方法，以正十六烷为基础油(烷烃类分子是基础油的主要成分，正十六烷分子结构简单，广泛应用于实际润滑试验和MD模拟中[18-20])，考虑润滑油中混入因磨损而产生的磨屑(Fe)，通过设置不同粒径的磨屑和油膜厚度，比较在不同载荷下润滑油膜的密度分布、压缩率，分析剪切过程中润滑体系的力学响应和不同粒径磨屑的动态行为特征，并进一步探究在乏油工况下磨屑对润滑油润滑性能的影响。

1 摩擦试验

微纳米划痕仪(MST)利用探针对待测样品表面进行划痕试验，可以测定摩擦过程中的摩擦因数、磨损率、应力-应变曲线等微观力学数据[21-24]。

试验主要原料和试剂包括：十六烷基础油(纯度99%，上海紫一试剂厂生产)；磨屑铁(纯度99.8%，粒径50 nm，南宫市鑫盾合金焊材喷涂有限公司生产)；分散剂三聚磷酸钠(纯度≥99.9%，无锡市亚泰联合化工有限公司生产)；基底材料为直径12 mm的纯铁(上表面粗糙度为Ra0.05～0.1 μm)；压头为直径1 mm的金属钢球。

称取一定质量的基础油、磨屑和分散剂混合并充分搅拌15 min，用超声波处理器振荡分散15 min，间隔5 min连续处理3次，得到质量分数为0.1%和0.5%的含磨屑润滑剂。

试验采用的微纳米划痕仪为奥地利Anton Paar公司生产的微纳米压/划痕仪(MST2)，如图1所示。试验时，首先用微纳米划痕仪首先对滴入润滑剂的基底进行预扫描，然后进行微纳米划痕试验。试验条件为：在30～100 mN的载荷作用下，探针以3 mm/min的速度滑动，滑动距离为3 mm。试验后采用光学显微镜对划痕形貌进行扫描。

图1 微纳米划痕仪

图2所示为不含磨屑和含磨屑润滑剂润滑时在不同负载下的摩擦力和正压力的变化情况。可以发现，在不同载荷条件下，含磨屑的润滑剂所对应的摩擦力FL均大于不含磨屑润滑剂所对应的摩擦力，并且磨屑的加入使得FL的振荡幅度增大。这一方面是由于磨屑的存在提高了润滑油的黏度，另一方面是由于在划痕试验过程中，划痕仪的压头与磨屑之间发生相互碰撞或挤压变形。

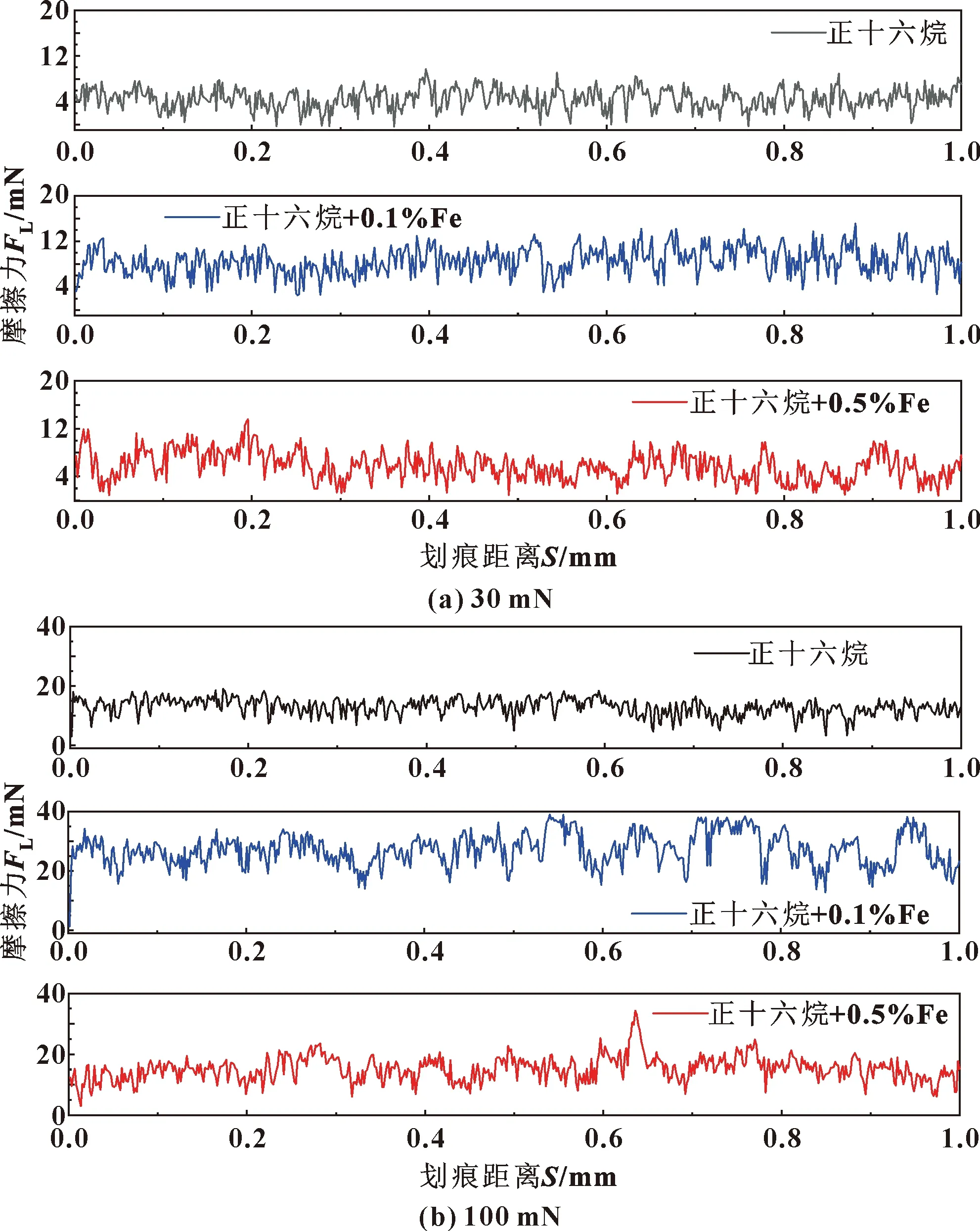
图2 不含磨屑和含磨屑润滑剂润滑时不同载荷下摩擦力FL的变化

图3所示为含磨屑润滑油在不同磨屑质量分数条件下的摩擦因数。可以发现，含质量分数0.5%磨屑的润滑油摩擦因数反而小于含质量分数0.1%磨屑的润滑油，这是由于适量的磨屑会沉积到壁面不平整部分，起到填充修补作用效应，同时还会在剪切过程中发生滚动，从而降低磨损。

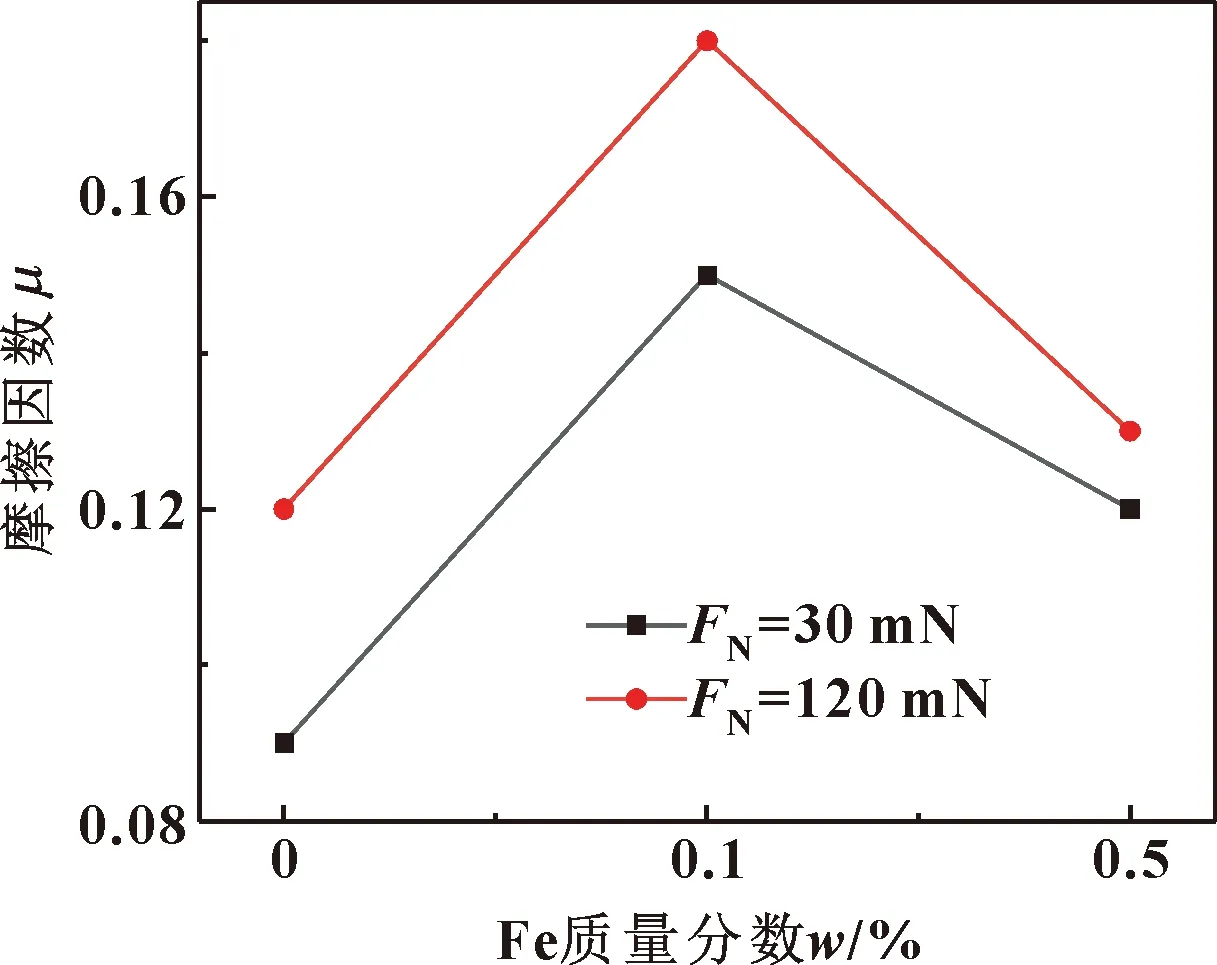
图3 含不同浓度铁屑润滑油的摩擦因数

图4所示为含磨屑润滑剂润滑下试样划痕形貌光学显微镜照片。可以看到含有磨屑润滑剂润滑下试样的划痕深度小于不含磨屑润滑剂润滑下的划痕深度，这是由于磨屑会吸附在摩擦表面形成保护层，避免摩擦副之间的直接接触。

图4 不同润滑剂润滑下同载荷下划痕形貌光学显微镜照片

2 分子动力学模拟

2.1 模型的建立

图5所示是MD模拟过程中所使用的纳米间隙润滑模型，x、y方向施加周期性边界条件，z方向施加非周期边界条件。模型在x、y方向的尺寸为13.8 nm×8.1 nm。上下平行壁面均为体心立方晶体Fe(100)晶面，壁面厚度为2.3 nm。上、下固体壁面均分为3层，用于施加边界条件的外层刚性层(黄色)、用于提供环境影响因素的中间层恒温层(绿色)、用于提取力学特性的内层自由变形层(紫色)。上、下壁面之间填充有润滑剂，包括正十六烷基础油(灰色)和磨屑Fe(绿色)。MD模拟受限于有限的计算机集群的计算量，无法做到完全实现实际试验条件。当磨屑过大时，会在压缩阶段便与壁面接触，无法达到研究的目的。经过模拟调试，确定磨屑Fe在润滑油中的体积分数为1.89%。不含磨屑Fe的润滑体系原子总数为79 320个(780个正十六烷分子)；含磨屑Fe的体系原子总数为79 322个(770个正十六烷分子，磨屑Fe的粒径为2.2 nm)。

图5 边界纳米润滑模型

2.2 模拟过程

MD模拟过程通过大规模原子/分子并行模拟器(Large-scale Atomic/Molecular Massively Parallel Simulator，LAMMPS)实现[24]。模拟中采用第二代力场COMPASS力场(Condensed-phase Optimized Molecular Potential for Atomistic Simulation Studies)对烷烃分子进行模拟[25]。金属壁面铁原子之间的相互作用采用Finnis-Sinclair(FS)EAM势函数[26]，其他不同分子上的原子和相同分子上间距在3个原子以上的原子之间的非键作用采用Lennard-Jones(L-J)势[27]，截断半径取1 nm。铁屑和壁面原子之间也使用L-J势，磨屑与壁面原子之间的作用参数为：ε壁-屑=12.33 kJ/mol，σ壁-屑=0.22 nm。其他原子有关的参数如表1所示。

表1 L-J参数

MD模拟过程包括弛豫、加压和剪切3个阶段。首先在NVT系综下对润滑剂分子和金属原子进行充分弛豫，弛豫时间为0.2 ns，使体系的总能量收敛于常数值1×10-6；随后在接下来的0.5 ns内用NVE系综代替NVT系综，并引入加压阶段，通过固定刚性层2并施加载荷于刚性层1达到加压的效果；将为了传导体系由于加压产生的热量，运用Nose-Hoover恒温方法控制恒温层3、4的温度，设置温度为303 K，温度阻尼系数设置为100 fs；最后在剪切阶段，沿x方向给上下壁面的刚性层施加大小相等，方向相反的速度±10 m/s。为了保证能够得到准确的数据，剪切运动的距离应大于13.8 nm，故模拟时间取1.4 ns。整个MD模拟的时间步长取1 fs。

3 结果和讨论

3.1 加压阶段

在实际应用中，通常假设润滑油是不可压缩的。但是当油膜厚度减小到纳米尺度时，润滑油的压缩性能对润滑系统的刚度、阻尼和摩擦学性能的影响不可忽略[28]。通过对润滑体系施加载荷，体系高度Lz会随着载荷的增加而逐渐减小，润滑油膜厚度变薄。通过比较润滑体系Lz的变化，可计算出润滑油的压缩率。加压阶段，沿z向给刚性层2分别施加0.25～2.0 GPa的载荷。为了保持磨屑Fe结构的稳定，先沿z向施加20 MPa的压力至体系高度稳定后，再继续施加到目标压力。

图6所示为不同润滑体系压缩率随载荷的变化。可以看出，磨屑的存在会降低油膜的压缩率，并且随着载荷的增加，磨屑对润滑体系油膜压缩率的影响越显著。当载荷从0.25 GPa增加到2.0 GPa时，两体系之间压缩率的差值从0.35%提高到1.05%，说明磨屑的存在能够提高油膜的抗压缩性能，并且随着压力的增大，效果越明显[29]。

图6 不同润滑体系的压缩率随载荷的变化

为了直观地观察体系中润滑油分子的分布情况，沿z方向将体系高度分为1 000等分，以原子中心所在位置为各原子的质心，计算出各等分中润滑油的密度，并在0.2 ns内取均值，从而得到密度分布曲线。图7(a)所示是不同载荷下不含磨屑的润滑体系在不同载荷下沿z向的密度分布曲线。基础油分子的密度分布曲线在壁面间发生振荡，近壁面处出现类固化现象。当pz不大于1.0 GPa时，密度分布曲线有7个波峰，6个波谷，且靠近壁面的波谷值接近0，可见油膜此时分为7层；当pz=1.5 GPa和2.0 GPa时，油膜密度峰值个数减少为6，中心层的密度降低，油膜分为6层，这是由于体系高度Lz在重载条件下降低，油膜厚度不足以形成7层结构。图8(a)所示是pz=1.5 GPa下的密度分布云图，可以看出不含磨屑的油膜此时分为6层，在中间区域呈现无序结构，表明流体分子纠缠。图7(b)所示是含有磨屑的润滑体系在不同载荷下，沿z向的密度分布曲线，可以观察到在重载条件下油膜仍分为7层，近壁面处的密度峰值和不含磨屑的润滑体系相近，这也进一步说明铁屑的存在提高了油膜的抗压缩性。图8(b)所示的密度分布云图也显示含磨屑润滑体系的油膜分为7层，但是磨屑的存在会使得润滑油分子的运动受到阻碍(虽然润滑体系已经是平衡状态，但是基础油分子始终处于运动状态)，从而对自身附近的密度分布产生一定的扰动，如图中红框部分所示。

图7 不同载荷下不同润滑体系沿z向的密度分布

图8 pz=1.5 GPa时不同润滑体系的密度分布云图

3.2 剪切阶段

当润滑体系加压到稳定状态后，润滑油分子充满上下固体壁面之间。此时保持体系的加压状态，并给体系的刚性层1、2在x向施加方向相反，大小为10 m/s的剪切速度。图9所示是在303 K、500 MPa和相对剪切速度为20 m/s条件下，不同润滑体系的速度分布。由于正十六烷为牛顿流体，在不考虑界面滑移时沿x向速度应是线性分布，如图中虚线所示。然而实际中，基础油分子的自身缠绕、在近壁面处的类固化和磨屑的运动，均会对体系的速度分布vx产生影响。在2种润滑体系中，远离金属壁面润滑剂的速度分布大致呈线性关系，而近壁面处润滑剂的速度分布呈非线性关系，且存在与壁面速度相同的区段。同时可以发现，含磨屑的润滑体系与不含磨屑的润滑体系的速度分布曲线并不会重合，说明磨屑的存在会影响润滑体系内流体流动，这一方面是由于磨屑导致流体黏度增加，另一方面是磨屑自身的运动状态扰乱了流体分子的运动。

图9 pz=1.5 GPa时不同润滑体系的速度分布

3.2.1 摩擦因数

图10所示是2种润滑体系在边界润滑状态下模拟得到的摩擦力FL与正压力FN的关系。可以看出，在0.25～2.0 GPa载荷条件下，含磨屑的润滑体系的摩擦力总是大于无磨屑的润滑体系，并且随着正压力的增大，2个体系摩擦力的差值也逐渐变大。这一结果和GHAFFARI等[30]得到的趋势一致，出现这种情况的原因是磨屑的存在使得润滑体系中润滑油的黏度升高，并且会加剧流体的无序流动，从而导致体系需要克服更大的力进行剪切运动。在纳米尺度下，物体之间的黏附力对润滑体系的力学结果有显著影响，因此在计算摩擦因数μ时，引入公式[31]

图10 含磨屑与不含磨屑润滑体系的摩擦力与正压力关系

FL=μ(L0+FN)=F0+μ·FN

(1)

式中：L0为恒定的影响因子；F0是摩擦力偏量(Derjaguin offset)。

用式(1)对MD模拟得到的结果进行拟合，拟合直线的y轴截距即为摩擦力偏量，斜率即为摩擦因数。因此，不含磨屑润滑体系的摩擦力偏量为20.24 eV/nm，摩擦因数为0.109，与试验得到的摩擦因数(0.09～0.12)吻合；含磨屑润滑体系的摩擦力偏量为22.68 eV/nm，摩擦因数为0.131，与试验得到的摩擦因数(0.12～0.18)吻合。

3.2.2 磨屑运动

磨屑在剪切过程中的运动同样也会影响着润滑油性能，但是这一现象很难通过试验观察到，而借助MD模拟能够直观地得到磨屑的动态运动过程。通过可视化软件OVITO处理输出文件，选取磨屑同一轴线上的原子，统计不同时刻下的原子坐标信息，从而计算在一段时间内的滚动角速度。图11所示是在剪切过程中磨屑沿着x轴的滚动，标记磨屑直径(红线)与水平线(绿线)的夹角α(磨屑在剪切过程中主要受到x向上的作用力，沿其他轴的滚动角度很少)。当时间t从0.45 ns到0.55 ns时，α从70°变成95°，说明磨屑在这个过程存在滚动；当t=0.65 ns时，α仍为95°，说明磨屑在0.55～0.65 ns阶段没有滚动，这可能是因为磨屑与上下壁面之间的相互作用力阻碍了磨屑的运动，此时磨屑与壁面之间是滑动摩擦；当t=1.3 ns时，α变成了-20°，磨屑再次发生滚动。在整个剪切过程中，磨屑同时存在滚动和滑动，说明在剪切中同时存在滚动摩擦和滑动摩擦。

图11 磨屑在剪切过程中的滚动

为了进一步了解磨屑的粒径对润滑油摩擦性能的影响，在不改变磨屑体积分数的前提下，将磨屑粒径D从2.2 nm分别减少至1.8和1.5 nm，此时润滑体系中磨屑的个数n相应地变为2个和3个(如图12所示)。如图13所示，通过比较在不同载荷下磨屑沿着x轴的角速度，可以发现3种粒径的磨屑均存在角速度接近于0的点，这也说明滑动摩擦和滚动摩擦同时存在于剪切过程中，符合图11中观察到的现象。图13(a)所示是pz=0.5 GPa时磨屑的角速度，可以发现粒径越小的磨屑在剪切过程中表现出的滚动角速度波动幅度更大以及拥有大的角速度极值，这是因为粒径小的磨屑受到油膜类固层的影响较小，并且固体壁面对磨屑的作用力降低，更容易产生滚动。图13(b)所示是pz=1.5 GPa时磨屑的角速度，磨屑的表现趋势与pz=0.5 GPa时相似，但是各个粒径的磨屑的角速度波动幅度和角速度最大值都减小，这是因为随着载荷的增加，油膜厚度减少，类固层油膜的密度变大阻碍磨屑的运动，壁面对磨屑的约束变大。

图13 不同载荷下不同粒径磨屑的角速度

此外，不同粒径磨屑在剪切过程中摩擦因数的值也不相同，D=1.5 nm磨屑的摩擦因数为0.118，而D=1.8 nm磨屑摩擦因数为0.123，均小于D=2.2 nm磨屑的摩擦因数，说明润滑体系的摩擦因数会随着磨屑粒径的增大而增大，也符合实际生产过程中观察到的现象[32]。一方面这是由于粒径越小的磨屑在剪切过程中滚动速度越大，破坏油膜的分层，导致流体紊乱；另一方面粒径的变化也会引起流体黏度的改变，这一现象符合NAMBURU等[33]的试验结果。

3.3 混合润滑

在精密机械和重载设备中，摩擦副两表面间间隙很小，往往难以形成完全流体润滑，而瞬时存在边界润滑或混合润滑状态。为了更好地探究在乏油工况下磨屑对润滑体系的影响，在上下壁面间设置少量润滑油分子(200个)，分析在剪切过程中润滑体系的摩擦因数、固体壁面的应力分布和磨屑的运动情况。此时润滑油膜无法承受载荷而发生破裂，上下固体壁面与磨屑直接接触。图14所示是载荷pz=0.75 GPa时，润滑体系的FL随时间的变化曲线。可见，不含磨屑的润滑体系在整个剪切过程中摩擦力均稳定在41 eV/nm附近，而含磨屑润滑体系的摩擦力均大于不含磨屑的润滑体系，这是由于磨屑与壁面的接触区域出现黏着磨损，阻碍壁面的运动。

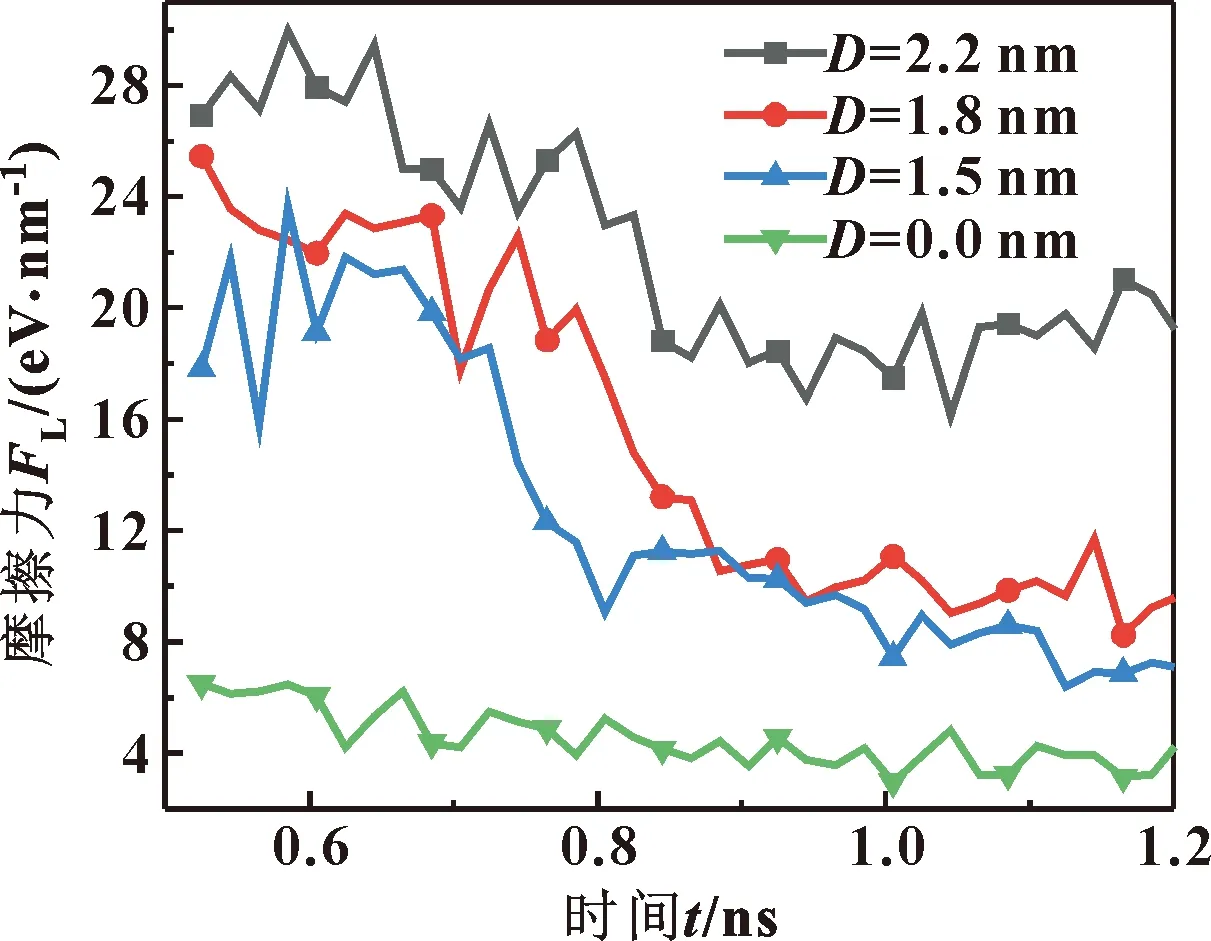
图14 pz=0.75 GPa时，不同粒径磨屑剪切过程中摩擦力随时间的变化

同时含不同磨屑的润滑体系在剪切过程中的摩擦力也不相同，随着磨屑粒径降低，磨屑与壁面的接触面积减小，剪切过程中的最大摩擦力也随之减小。在t=0.66～1.35 ns内，含1个磨屑润滑体系的摩擦力从257 eV/nm降低到171 eV/nm，含2个磨屑润滑体系的摩擦力从223 eV/nm降低到99 eV/nm，含 3个磨屑润滑体系的摩擦力从231 eV/nm降低到78 eV/nm。润滑体系摩擦力出现减小的原因是磨屑在挤压作用下发生塑性变形，随着剪切过程吸附在上下固体壁面，粒径小的磨屑甚至会进一步地发生破碎。在t=1.35～1.5 ns内，含2个和3个磨屑润滑体系摩擦力出现振荡增加，这是由于润滑体系进入新一轮剪切过程，随着固体壁面的运动过程，吸附在上下固体壁面的破碎磨屑产生接触，增大了体系的摩擦力。这也符合实际工况中，当过量磨屑进入零部件润滑区域时，会破坏润滑油膜，导致进一步磨损引发零件失效[34]。同时，粘附在壁面上的磨屑碎片会形成一层“保护层”，防止上下壁面直接接触破坏表面形貌，与试验观察到的现象相符。

图15所示是在载荷pz=0.75 GPa、t=0.55 ns时，含不同粒径磨屑润滑体系的von Mises应力云图。可以发现，磨屑在上壁面的挤压作用下发生严重形变，并且粒径小的磨屑变形现象最为严重，发生破碎。3种润滑体系中的最大应力均出现在磨屑内部，并且随着磨屑粒径变小，内应力逐渐增大，磨屑最大应力值分别为28.3、29.5和30.1 GPa，这也符合小粒径的磨屑在剪切过程中比较容易发生破碎的现象。图16所示是在载荷pz=1.50 GPa时，含D=2.2 nm磨屑的润滑体系在不同时刻下的von Mises应力云图，可以发现在重载作用下，磨屑的变形程度加剧，内应力相应增大至32.8 GPa，并且在t=0.95 ns时磨屑发生破碎，粘附在固体壁面。进一步说明大粒径的磨屑会恶化润滑油的摩擦性能。

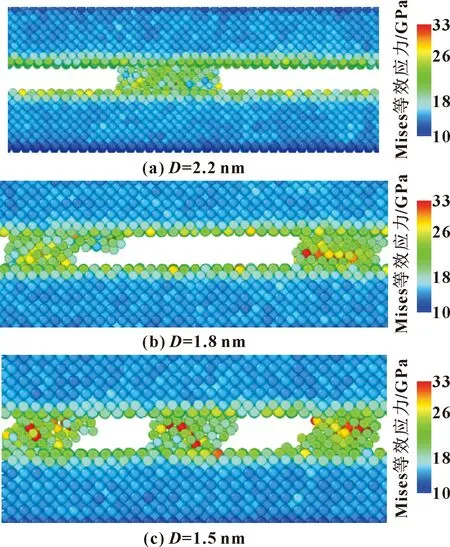
图15 pz=0.75 GPa，t=0.55 ns时，含不同粒径磨屑润滑体系的应力分布

图16 pz=1.50 GPa，D=2.2 nm时，润滑体系不同时刻下的应力分布

4 结论

(1)MD模拟得到不含磨屑的润滑体系在边界润滑状态的摩擦因数为0.109，含有磨屑的润滑体系在边界润滑状态的摩擦因数为0.131，符合磨屑的摩擦学试验结果；含小粒径磨屑的润滑体系的摩擦因数比含大粒径磨屑的润滑体系的小，说明磨屑聚集长大现象会恶化润滑油的润滑性能。

(2)磨屑的存在会降低油膜的压缩率；在载荷作用下，不含磨屑的润滑体系和含有磨屑的润滑体系均出现分层现象；重载条件下，磨屑的存在会影响油膜的分层现象，并且对磨屑附近的密度分布产生一定的扰动。

(3)在剪切过程中，磨屑同时存在滑动摩擦和滚动摩擦；在乏油工况下，粒径小的磨屑在剪切过程中更容易发生变形破碎。