热力变形下渣浆泵机械密封干摩擦磨损分析*
殷润生 穆塔里夫·阿赫迈德 耿 军
(新疆大学机械工程学院 新疆乌鲁木齐 830047)
在设备起停阶段或出现操作失误时,机械密封在干摩擦状态下运转,密封环端面会产生远高于润滑条件下的高温及磨损[1],严重影响机械密封的使用性能和寿命,导致生产中断。因此,准确预测干摩擦状态下机械密封的磨损及使用寿命,对保持设备安全及维持生产稳定有重要意义。针对机械密封摩擦副密封环磨损及热力变形,目前已有较多研究。其中磨损研究大多数集中于检测不同材料摩擦副的耐磨性[2-6],或表面不同涂层的耐磨性[7-11],工况集中在干摩擦[12-15],而对生产实际中机械密封的磨损研究较少。还有学者假设磨损痕迹存在从而计算磨损对密封性能的影响[16],或基于Archard磨损理论和分形理论,建立了机械密封端面磨损的分形函数模型[17-20]。在机械密封热力变形研究领域,学者们通过仿真或数值计算来获得机械密封端面温度场,但因对流换热系数缺乏固定算法,常根据边界条件选择近似模型的对流换热系数计算公式来替代[21-24]。还有学者在对机械密封温度场研究的基础上,提出了新的端面温度冷却方案[25-28]。目前,对于机械密封磨损的研究集中在检测干摩擦下不同材料或不同涂层的抗磨性,对生产实际中机械密封的磨损研究较少。
本文作者以YWN8合金接触式机械密封为研究对象,通过试验测量材料的硬度、磨损系数、干摩擦因数;建立了基于热力变形的机械密封磨损数值模型,对机械密封磨损进行数值模拟,得到了单力场及热力变形下摩擦副密封环的磨损深度,对比了磨损理论值,分析了热力变形下磨损深度与理论值不符的原因,为进一步研究打下了基础。
1 数值分析
1.1 双端面机械密封工作原理
以渣浆泵双端面机械密封为研究对象,如图1所示,密封介质为磷矿浆,内部导入冷却水。因密封介质颗粒多、硬度大,因此动静环采用相同硬质材料,为YWN8合金。

图1 渣浆泵双端面机械密封轴截面示意
从图1中取出一个因干摩擦失效的摩擦副密封环,如图2所示。可见,密封环表面出现热裂纹和磨损,判断该机械密封失效由磨损和热力变形导致,因此文中通过建立干摩擦下基于热力变形的机械密封磨损数值模型,对其磨损情况进行分析。

图2 机械密封端面磨损情况
1.2 数值模型
对一对摩擦副密封环进行建模,其三维模型如图3所示。密封环和密封环座尺寸见表1,具体材料参数见表2。

图3 机械密封摩擦副密封环三维模型

表1 机械密封摩擦副密封环尺寸 单位:mm
对模型进行网格划分,并做网格无关性验证,如图4所示。可知,当网格大于187 134后,其结果基本不变,因此网格数选择为187 134。
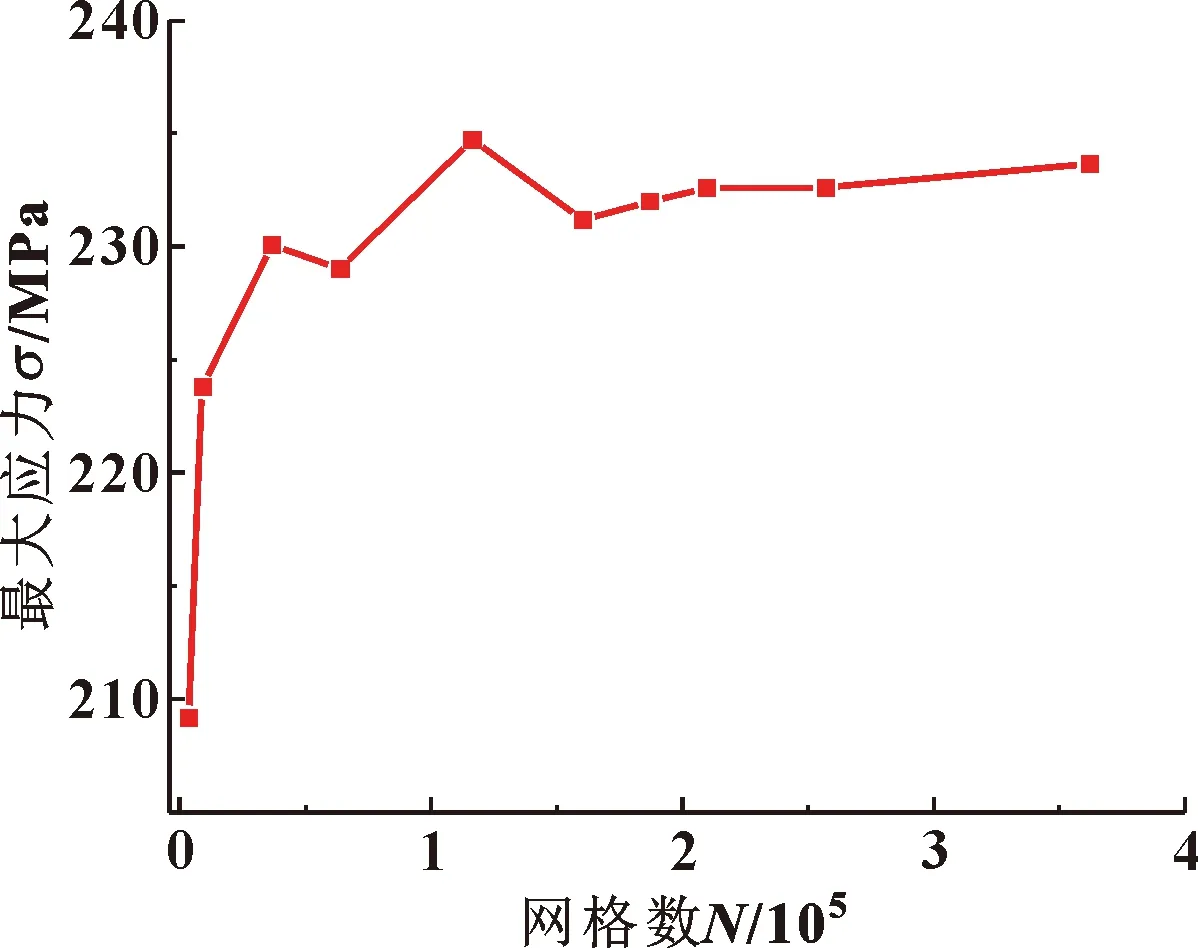
图4 网格无关性验证
1.3 边界条件
干摩擦运转时,密封环端面受弹簧压力作用,选取0.14、0.18、0.22、0.26 MPa 4组弹簧比压作为变量,旋转速度为研究对象实际工作转速1 450 r/min。
摩擦热为热源,热量由端面沿轴向传给动静环,动静环与空气产生对流换热,与密封腔接触面产生固体界面接触换热。
机械密封动静环间摩擦热流密度计算公式[29]为
q=fvpc
(1)
式中:q为热流密度,W/m2;f为干摩擦因数,由试验测得为0.1~0.2,文中选择为0.15;v为动环端面线速度,m/s,pc为端面比压,MPa。
计算得到热流密度后需计算动静环热量分配占比。用公式(3)计算:
(2)
式中:qj为静环端面分配热流;qd为动环端面分配热流;hd为动环轴向尺寸;hj为静环轴向尺寸;λd为动环热导率;λj为静环热导率。
为了方便计算,通常将于空气换热设置为隔热,密封件与密封腔接触部分存在固体界面接触换热,数值从文献[30]中查出。其他参数见表1和2。
为了论述的清晰,我们按照受调查人员是否作为交际一方参与了自然发生的真实交际,将语用学研究中常用的语料收集方法分为“自然语料”和“引发式语料”两大类:自然语料来自于受调查人员作为交际一方参与其中的言语交际行为,受真实交际意愿的驱动;引发式语料是指研究对象并没有参与到真实的言语交际中,而是受研究工具的诱发和引导,从记忆中搜寻有关语言使用的信息,并报告出来,表演出来,或写出来,受研究人员的研究目的驱动。
1.4 磨损条件
文中磨损理论采用ARCHARD磨损理论,见公式(3)
(3)
式中:γ为机械密封磨损深度,μm,Kw为磨损系数,为方便计算,假定文中磨损处于稳定磨损阶段,磨损系数不变;K/H为磨损率,mm3/(N·m);pc为端面比压;v为动环端面线速度;H为摩擦副密封环布氏硬度,具体数值见表2。其中材料磨损系数和硬度需通过试验测量。
2 试验研究
2.1 试验系统与方法
YWN8合金硬度通过HRS-150型数显洛氏硬度计测量。磨损系数及干摩擦因数用M2000型磨损试验机测量,试验后使用VHX-6000超景深显微镜进行三维可视化采集。
将干摩擦损坏密封环及同尺寸崭新密封环各一个,分别切割成36份,1份用铜粉焊镶嵌在长方体底座作为1个试件,每个密封环做12个试件。图5所示为试件样品,表面微坑来源于硬度测试。图6所示为磨损试验机工作原理及有限元模型,底座被夹具夹住保持静止,摩擦副与密封环干摩擦接触并随磨损试验机转动。摩擦副与密封环材料为YWN8,底座材料为铸铁。

图5 试验样品

图6 试验工作原理
试验在M-2000型磨损试验机上进行,试验转速为180 r/min,载荷分别为50、70、90、110 N,每组试验参数下测试3次。文献[29]提到机械密封磨损深度单位为μm/h,因此单次试验时间为1 h。试验后用超景深显微镜三维可视化采集磨损表面形貌及三维高度。以180 r/min、50 N试件为例,其试验后磨损表面形貌及三维高度如图7所示。
2.2 试验结果
通过测试,崭新合金环硬度为71HRC,干摩擦损坏后硬度下降21%,为56HRC,之后将其转化为布氏硬度。
通过磨损试验,崭新合金环磨损试验数据见表3,磨损系数为1.2×10-6,转为磨损率为1.41×10-6mm3/(N·m)。文献[31-32]中该值为1.2×10-6mm3/(N·m),数据基本一致,判定试验结果准确。有细微差距的原因是文献中的镍基碳化钨含镍量比文中材料高,更加耐磨。

表3 YWN8密封环试验数据
2.3 磨损数值模型验证
因全尺寸试验成本较高,因此通过模拟磨损试验来部分验证数值模型的准确性。试验有限元模型见图6,边界条件采用试验参数。将仿真磨损深度与超景深扫描深度进行对比,如图8所示。可知最大深度误差在10%以内,试验磨损深度较大是因为试验中存在磨粒磨损等其他磨损形式,并随着压力的增大,磨粒产生越快,磨粒磨损越多。以180 r/min、50 N试件为例,其仿真磨损形貌如图9所示。与试件端面磨损表面三维高度图(见图7(b))对比可知,仿真磨损形貌与试件磨损形貌基本一致,均是中部最深延两端及远处逐渐变浅的趋势。经过对比证明磨损数值模型准确,可用于机械密封干摩擦磨损仿真。

图8 试验和仿真磨损深度对比
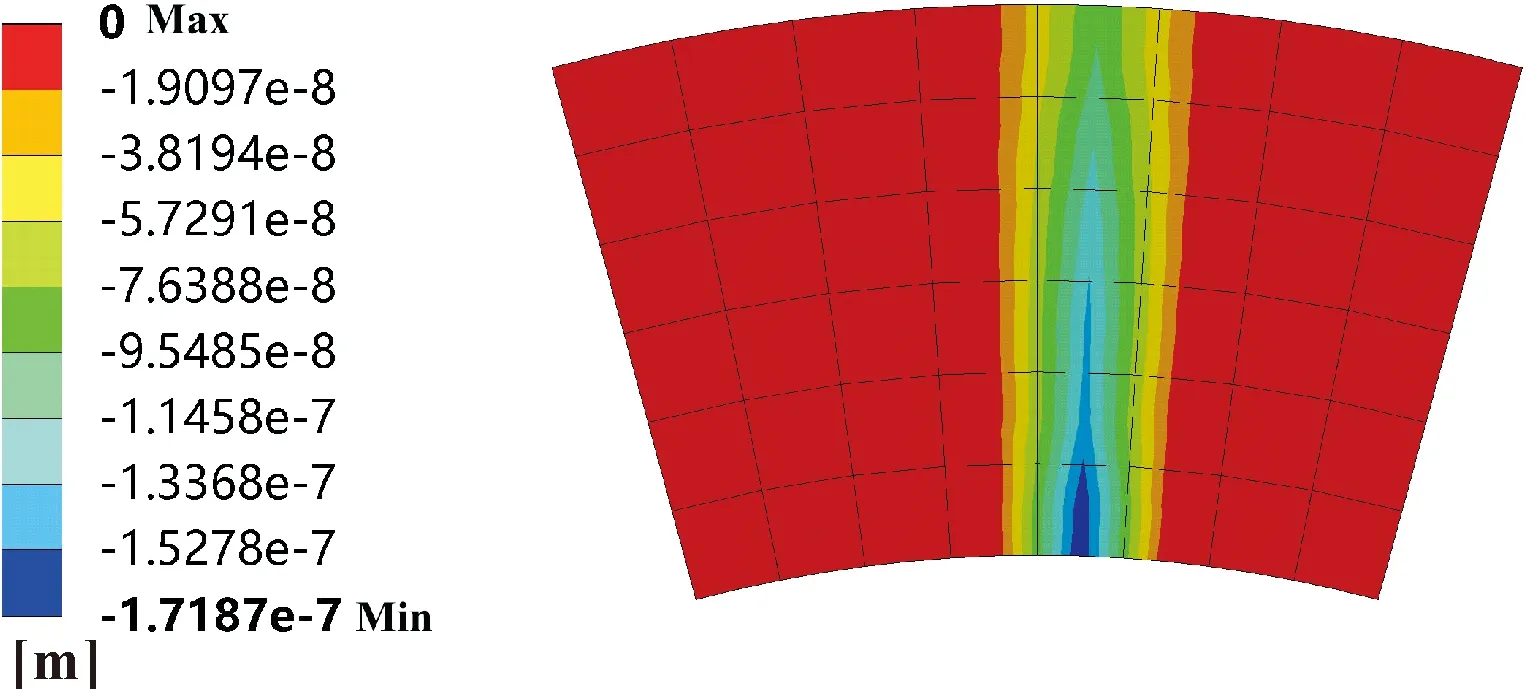
图9 有限元仿真得到的磨损形貌
3 结果与讨论
使用ANSYS的热力模块,将边界条件加载到密封环上,插入WEAR指令,输入材料磨损系数及硬度,增加用户自定义结果,求解干摩擦运转时密封环温度场云图、热力变形情况,单力场及热力变形下磨损形貌及磨损深度。
3.1 热力变形分析
外界温度为20 ℃、弹簧比压为0.26 MPa、转速为1 450 r/min时,干摩擦工况下密封环的温度场云图如图10所示。动静环温度从端面延轴向递减,靠近外侧处因和端盖或弹簧座相连存在固体界面接触换热,因此温度较低。最高温度在内径处,为84.555 ℃。从最高温度可知,温度并非该类机械密封失效的主要原因。
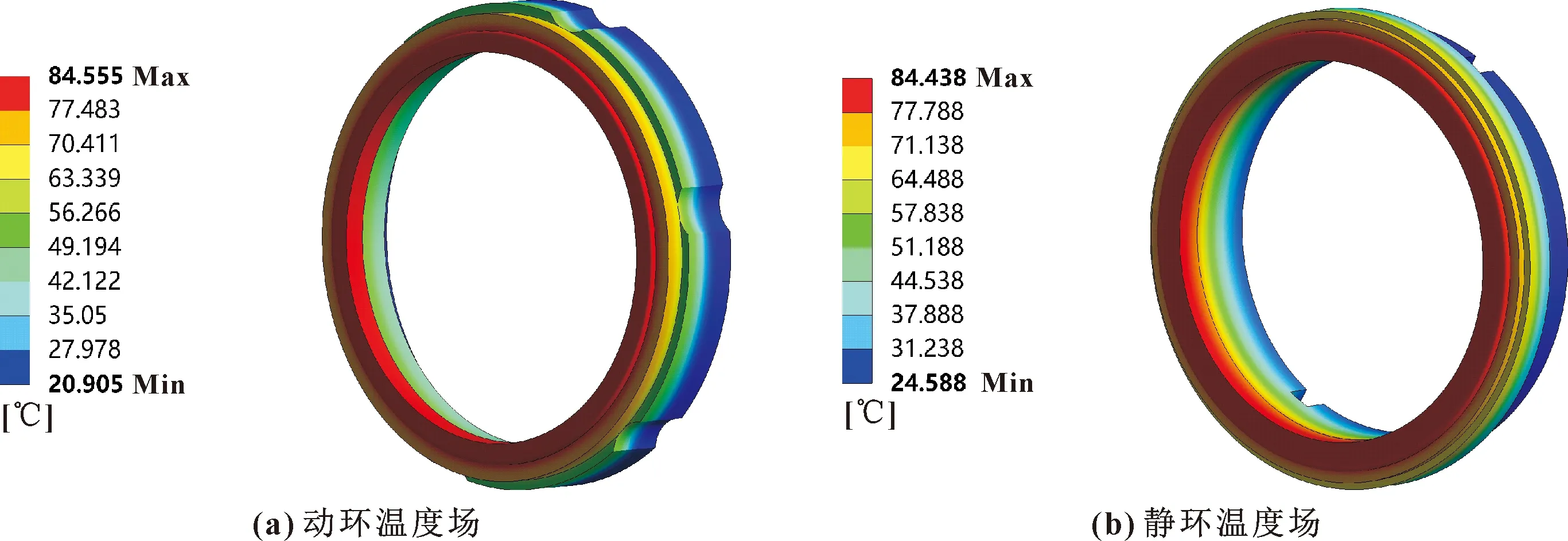
图10 干摩擦工况下密封环温度场云图
图11(a)所示为干摩擦下密封环端面的变形趋势云图,可知密封面由平行面转变为收敛面,之后内径将相对外径磨损更严重。
如图11(b)、(c)所示,内外径之间出现了间隙,密封环内径最大出现1.52 μm的间隙,这将导致端面粗糙峰接触面积减少,端面黏着磨损较热力变形前呈下降趋势,后续仿真结果证明了该观点。

图11 动静环热力变形云图
3.2 磨损分析
文中从端面磨损形貌和磨损深度两个角度分析仿真数值模型的准确性。
图12所示为热力变形下的仿真磨损云图。可见内径磨损情况较为严重,这和图2中实际端面磨损情况相符,证明仿真结果准确,原因是热力变形下,内径处变形相对外径更大,因此磨损较外径更为严重。

图12 机械密封磨损云图
图13所示为理论磨损深度、单力场仿真磨损深度与热力变形下仿真磨损深度的对比。理论磨损值与单力场磨损值误差在5%以内,因为其均只考虑了压力与转速对磨损的影响,同时也证明了有限元模型计算准确。
图13中,加入温度场影响后,磨损深度大幅度下降,但根据两点原因推断其磨损值更符合实际:
(1)学者们已多次证明多物理场下机械密封变形、应力等参数比单物理场时更符合实际[23-24];
(2)在文中热力变形中分析时,已推断出密封环热力变形后端面黏着磨损较变形前呈下降趋势,而理论公式并未考虑端面变形对磨损的影响。
综上所述,热力变形下机械密封磨损值比理论值和单力场值更加准确,未来研究可考虑在Archard公式中增加代表温度场的影响因子,从而使公式更准确。
4 结论
通过热力变形下的磨损计算,分析YWN8合金机械密封摩擦副密封环的温度场和磨损形貌、磨损深度,试验测量了合金的硬度、磨损系数、干摩擦因数。得到以下结论:
(1)干摩擦工况下密封环端面温升较低,因此温度并非该类机械密封失效的主要原因。
(2)热力变形后端面形成收敛面,内径变形更大,因此内径磨损较外径更为严重,和实际相符。
(3)热力变形下密封面内外径间隙增大,造成端面粗糙峰接触面积减小,黏着磨损较变形前呈下降趋势,造成磨损深度与理论值不符。
(4)热力变形下磨损有限元模型能较为准确地计算密封环磨损深度,未来研究可考虑在Archard公式中增加代表温度场的影响因子,从而使公式更准确。

