铁道车辆车轮踏面反向优化设计方法
干 锋, 戴焕云, 池茂儒, 高 浩
(西南交通大学 牵引动力国家重点实验室, 四川 成都 610031)
铁道车辆在线路上运行的全部质量由与钢轨接触的车轮踏面承担,车辆的运行和导向通过轮轨黏着产生的牵引力和制动力实现。对于铁道车辆,设计较好的踏面和轨面外形可得到理想的车辆运行性能,包括曲线通过性能、脱轨安全性、运行平稳性和安全性[1]。在踏面和轨面外形设计方面,国内外科研工作者做了大量的研究,针对不同的目标和策略提出了众多外形设计方法。V. L. Markin[2]、I.Y. Shevtsov[3]等在测量车轮踏面和轨面外形基础上根据给定的轮径差设计出新踏面以得到最优的车辆动力学性能;Hamid Jahed[4]等采用给定的轨面和轮径差信息,建立以轮径差误差最小化为目标的最优化模型设计出最优踏面,并通过动力学仿真软件验证;G. Shen[5]等给出一种根据接触角和轨面外形反向设计踏面的方法,并开发出专用的计算程序;同时G. Shen[6]等也给出一种以轮径差误差最小化为目标的踏面设计方法;O. Polach[7]给出一种以等效锥度为目标的踏面设计方法;M. Ignesti[8-9]等根据磨耗模型给出磨耗踏面设计方法;M. Novales[10]和J. SANTAMARIA[11]分别根据遗传算法给出一种踏面外形优化的方法。因此踏面外形设计根据设计原理可分为以轮径差为目标[2-4],以接触角为目标[5-6],以等效锥度为目标[7],根据磨耗后踏面外形设计[8-9,12]和根据轨面外形进行扩展[13],以及采用遗传算法进行踏面设计[10-11]。
车轮踏面外形是影响高速列车动力学性能的重要因素,CRH2型高速动车组采用LMA踏面,CRH3型高速动车组采用S1002CN踏面。从线路运营情况和试验台试验结果看,这些踏面基本上满足动力学要求[14]。但当车辆运行在某些特殊路段,出现报警和晃车等问题,因此有必要研究不同类型的车轮踏面与钢轨轨面配合时的轮轨接触关系以及轮轨接触点分布特征,同时也为现阶段标准动车组新型踏面的设计提供理论和技术支持。
现阶段标准车轮踏面和轨道型面由多段不同半径的圆弧曲线和直线段组成[15]。由于车轮踏面在与轨面相接触时受到轨道的约束,轮对在不同横移量下的轮径差、接触角和等效锥度不断变化,动态接触关系复杂,因此很难从轮轨接触几何参数中得到与踏面和轨面外形相关的解析表达式。为此本文给出一种踏面反向设计方法,即以轮径差为目标,建立以踏面外形误差最小化为目标的最优化模型,在已知初始踏面、轨面外形和轮径差曲线的基础上,给定轮轨初始接触点位置,采用循环迭代的数值计算方法,得出最优的踏面反向设计参数以及与初始踏面基本一致的踏面外形。与其他方法不同的是,本计算方法在满足轮径差的同时,可根据需要控制设计出的踏面外形以及轮轨初始接触点位置。
1 轮轨几何接触特征分析
铁道车辆系统动力学性能的非线性在很大程度上是轮轨接触的几何非线性。为了准确得到标准踏面轮轨几何接触的特征,以标准S1002CN和LMA踏面为例(见图1),分析其轮径差、接触角以及接触点分布的特征,为车轮踏面反向设计的假设条件提供依据。轮轨接触几何关系计算参数见表1。

表1 轮轨接触几何关系计算参数
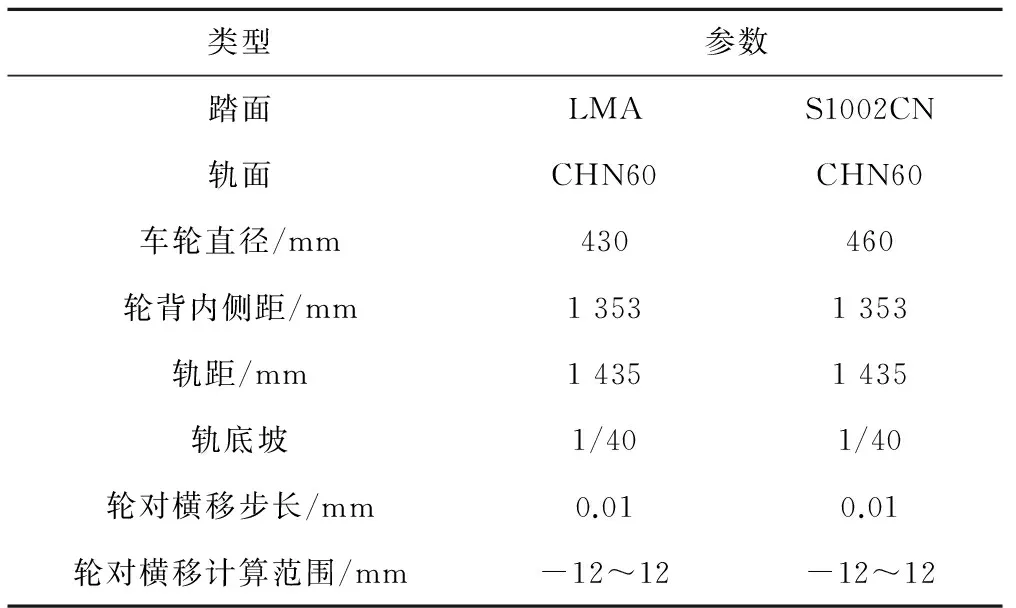
类型参数踏面LMAS1002CN轨面CHN60CHN60车轮直径/mm430460轮背内侧距/mm13531353轨距/mm14351435轨底坡1/401/40轮对横移步长/mm0.010.01轮对横移计算范围/mm-12~12-12~12
文献[16]计算轮径差和等效锥度时可不考虑轮对在轨道上横移产生的侧滚。因此当不调整轮对侧滚时,自编软件ProGeom和商业软件SIMPACK计算得到的轮轨接触几何关系见图2。
由图2(a)可见,在踏面外形的轮缘最高点处,左侧和右侧的斜率方向相反,轮缘左侧的斜率均为正,右侧的斜率均为负。轮缘最高点右侧的踏面外形虽然单调递减,但其斜率变化波动较大,因此2种类型踏面外形的斜率都不具有单调性。在-30~40 mm处单调性也不明显。而CHN60轨面外形的斜率具有单调性。
由图2(b)可见,S1002CN和LMA踏面的轮径差随着轮对横移量的增大而增大,具有单调性。
由图2(c)可见,S1002CN踏面的等效锥度随着轮对横移量的变化不具有单调性,而LMA踏面的等效锥度随轮对横移量的变化具有单调性。
由图2(d)可见,对于右轮,当轮对正向横移时接触角变化较大,同时当轮缘接触时接触角会减小;当轮对负向移动时接触角变化较小,不具有单调性。
由图2(e)和图2(f)可见,在刚性轮轨接触下,S1002CN踏面初始接触点横坐标为-4.6 mm,与轨面的初始接触点横坐标为-10.2 mm;LMA踏面初始接触点横坐标为6 mm,与轨面的初始接触点横坐标为0.5 mm;同时踏面上的接触点随着轮对横移量的增大依次顺序接触,具有一定的单调性;对于轨面上的接触点,在轮对横移量为负时会出现重复接触,不具有单调性。

由图2(g)可见,在刚性轮轨接触下踏面和轨面上会出现间断接触的区域,这是由于标准踏面和轨面都是由多段直线段和曲线段组成,轮对在横移过程中踏面上的直线段或曲线段不能完全与轨面相接触。这从图2(h)中也可看出。图2(g)中接触线上方的数字为轮对横移量,轮对左移为负,右移为正,单步横移量为0.01 mm。图2(h)中y为轮对横移量。
由表2可见,只有轨面斜率、轮径差和踏面接触点横坐标具有单调性。因此本文中提出的踏面反向设计方法可以基于以下基本假设条件:
(1) 轨面上各点的斜率须具有一定的单调性,左侧轨面上的点斜率依次单调递减,右侧轨面上的点斜率依次单调递增;
(2) 给定的轮径差须随着轮对的横移量依次单调递增;
(3) 在不同轮对横移量下设计出的踏面接触点坐标也具有一定的单调性;
(4) 轮对在轨面上横移时不考虑轮对的侧滚。

表2 轮轨接触各项指标单调性
轮轨初始接触点位置对轮轨接触来说非常重要,踏面上的初始接触点决定踏面磨耗集中的区域;轨面上的初始接触点决定轨面接触光带集中的区域。
在给定的轮轨初始接触点和以上4条基本假设条件即可进行踏面反向设计。
2 踏面反向设计原理
由于踏面外形有部分区段不与轨面相接触,用轮径差进行踏面反向设计时,踏面不接触区域将无法进行设计,因此需要与参考踏面相结合才能组成完整的车轮踏面外形。反向设计出的踏面由参考踏面、设计踏面和二者之间的过渡段组成,见图3。在不同设计参数下过渡段的位置不固定,需要根据设计踏面的大小进行调整。
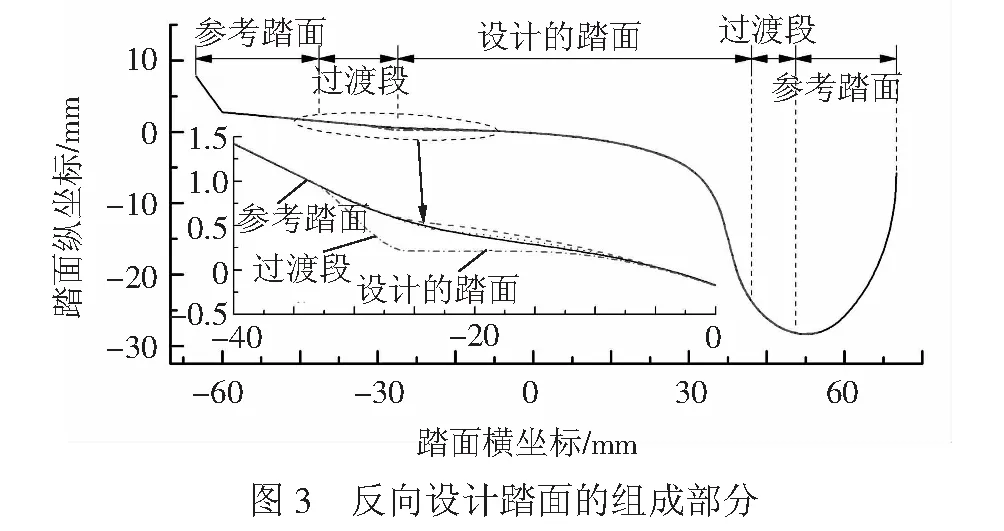
假设踏面外形可以用表达式fw(x)表示,轨面外形可用表达式fR(x)表示,则踏面和轨面的斜率可分别表示为
( 1 )
对于在一定轨面外形fR(x)下踏面的反向设计,在已知不同轮对横移量s下的轮径差函数R(s),轮轨初始接触点p0和q0时,需求出对应踏面外形fw(x)。


R(s)=RL(s)+RR(s)
( 2 )
其中
此时接触半带宽计算式为
( 3 )
由于只有一个轮径差约束条件,而左右轮接触点坐标有4个未知数,因此需要再给出其他3个约束条件才能惟一确定左右轮接触点的位置。
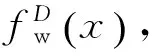
( 4 )
优化的目标函数可写成

( 5 )
由图4(b)中可见
( 6 )
令η为给定的轮径差变化量ΔR(s)在左右踏面中的分配比例,即
( 7 )
由于轮对横移是一个连续的过程,且轮对踏面与轨面接触时沿轨面切线方向,则从s-Δs移动至s时ΔRL(s)和ΔRR(s)可表示为
( 8 )
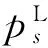
κ=ξ·KR(xs-Δs)
( 9 )

当KR(xs)<κ时,KR(xs)=KR(xs);
当KR(xs)≥κ时,KR(xs)=κ。

在实际踏面反向设计时,需采用循环迭代的数值计算方法。计算过程为

(1) 在一定的给定轮对横移量s、横移步长Δs和参数ξ下,以给定轮轨初始接触点位置为起点,按照该轮对横移量s下的轮径差的要求得到此时的踏面外形点;
(2) 依次循环迭代轮对横移量s,得到设计的踏面外形;
(3) 调整参数ξ以获得最优的踏面外形。
3 标准踏面反向设计
为了验证踏面反向设计方法的可行性,针对S1002CN踏面,给定轮径差如图2(b)中S1002CN曲线,初始接触点位置在相对轨面中心-10.2 mm处。在不同ξ下的计算结果见图6。
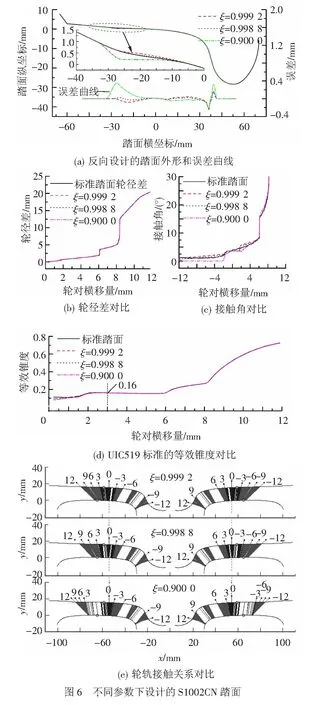
由图6(a)中可见,对于S1002CN踏面,不同参数ξ下可得到不同的踏面外形,但均与标准踏面存在一定的误差。设计误差为标准踏面与设计踏面垂向坐标之差,设计的踏面坐标点在标准踏面之下为正,反之为负。在ξ=0.998 8时,设计误差最小,小于0.26 mm。由图6(b)~图6(d)中可见,不同参数ξ得到的轮径差和等效锥度与标准踏面轮径差基本一致,但接触角有所差别。这是由于踏面的接触角由接触点所在的位置决定的,不同的参数ξ得到的轮轨接触点分布有所差异,见图6(e)。此外,不同参数ξ设计的踏面的初始接触点位置与给定的初始接触点位置一致。

针对LMA踏面,给定轮径差图2(b)中LMA曲线所示,初始接触点位置在相对轨面中心0.5mm处。在不同ξ下的计算结果见图7。
由图7可见,对于LMA踏面反向设计可以得出与S1002CN踏面一致的结论,但在ξ=1.000 0时,设计误差最小,小于0.2 mm。
从以上分析结果中可以看出,S1002CN和LMA踏面通过了踏面反向设计的验证。但反向设计的踏面不能与标准踏面完全一致,可能的原因有
(1) 反向设计的踏面与标准踏面设计原理不一致;
(2) 对于给定的轮径差曲线,其计算时有一定误差;
(3) 反向设计过程的计算误差,如式( 8 )中积分误差;
(4) 踏面反向设计原理中定义的规则不够全面。
对于误差第1项是存在的,第2和第3项可通过提高计算精度解决,第4项需要完善反向设计原理。对于本文中的设计误差,基本满足设计要求。
等效锥度作为轮轨接触线性化指标,被广泛用于表征轮轨接触几何的特征[17]。文献[18-19]规定车辆进行试验时用该参数来评估轮轨接触几何关系。国际铁路联盟标准UIC519[16]定义名义等效锥度为轮对蛇行运动幅值为3 mm时对应的等效锥度。由于设计的踏面未改变原有的轮径差,因此从等效锥度计算方法[20]可看出,设计踏面未改变原踏面的等效锥度。
4 给定轮径差下的踏面反向设计
为了验证踏面反向设计方法对任意修改后的轮径差的适应性,在标准S1002CN踏面轮径差的基础上进行了局部修改。标准轮径差与修改后轮径差见图8(a)。在参数ξ=0.998 8时,设计出的踏面与标准踏面对比见图8(b) ~图8(d)。
由图8(a)、8(b)可见,修改后的轮径差与设计的轮径差基本一致。由图8(c)可见,修改后的轮径差对踏面外形的影响体现在轮缘根部。由图8(d)可见,设计的踏面与标准S1002CN踏面在轮对横移量为3 mm处均为0.16。为了满足轮径差的要求,在轮缘根部设计出的部分踏面外形偏向标准踏面的轮缘内侧,因此轮轨间隙有所增大,这从设计踏面的等效锥度变化曲线中也可看出。由图8(e)可见,新设计的踏面接触点分布较标准踏面均匀。
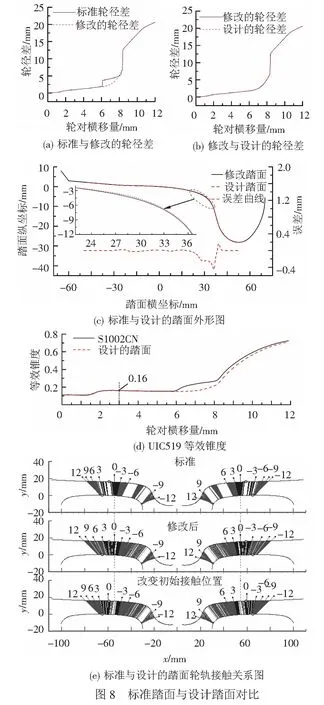
在给定的修改后轮径差的基础上,改变轮轨初始接触点位置,由原始的-10.2 mm变为-5 mm,得到的轮轨接触关系见图8(d)。由此可看出,在相同的轮径差曲线下,对于不同的轮轨初始接触点位置本文中给出的踏面反向设计方法同样适用。
5 总结
(1) 针对不同类型的标准车轮踏面,本文给出的踏面反向设计方法,能适应不同轮径差和轮轨初始接触点下车轮踏面的反向设计。
(2) 建立踏面设计的优化模型,在满足给定轮径差和轮轨初始接触点位置的同时,给出最优踏面设计外形。设计的踏面外形在不同轮对横移量下接触点分布更均匀。由于设计的踏面不改变不同轮对横移量下的轮径差,因此不会改变踏面原有的等效锥度。
(3) 本文中的踏面反向设计方法是在4个假设条件基础上,具有一定的使用范围。对于具有凹形磨耗的磨耗后踏面,由于其与轨面接触时的接触点处的斜率不一定具有单调性,本方法对该类型踏面的反向设计可能会不适用,这也为下一步踏面反向优化设计提供研究目标。
(4) 在标准踏面外形和轮径差的基础上,可任意修改轮径差曲线和轮轨初始接触点位置,得到所需的踏面外形,可为新型踏面设计提供参考。
参考文献:
[1] ENBLOM R. Deterioration Mechanisms in the Wheel-rail Interface with Focus on Wear Prediction:A Literature Review[J]. Vehicle System Dynamics, 2009, 47(6): 661-700.
[2] MARKINE V L, SHEVTSOV I Y, ESVELD C. An Inverse Shape Design Method for Railway Wheel Profiles[J]. Structural and Multidisciplinary Optimization, 2007, 33(3): 243-253.
[3] SHEVTSOV I Y, MARKINE V L, ESVELD C. Optimal Design of Wheel Profile for Railway Vehicles[J]. Wear, 2005, 258(7): 1022-1030.
[4] JAHED H, FARSHI B, ESHRAGHI M A, et al. A Numerical Optimization Technique for Design of Wheel Profiles[J]. Wear, 2008, 264(1): 1-10.
[5] SHEN G, AYASSE J B, CHOLLET H, et al. A Unique Design Method for Wheel Profiles by Considering the Contact Angle Function[J].Journal of Rail and Rapid Transit, 2003, 217(1): 25-30.
[6] SHEN G, ZHONG X. A Design Method for Wheel Profiles According to the Rolling Radius Difference Function[J].Journal of Rail and Rapid Transit, 2011, 225(5): 457-462.
[7] POLACH O. Wheel Profile Design for Target Conicity and Wide Tread Wear Spreading[J]. Wear, 2011, 271(1): 195-202.
[8] IGNESTI M, INNOCENTI A, MARINI L, et al. Wheel Profile Optimization on Railway Vehicles from the Wear Viewpoint[J]. International Journal of Non-linear Mechanics, 2013, 53: 41-54.
[9] IGNESTI M, MALVEZZI M, MARINI L, et al. Development of a Wear Model for the Prediction of Wheel and Rail Profile Evolution in Railway Systems[J]. Wear, 2012, 284-285:1-17.
[10] NOVALES M, ORRO A, BUGARIN M R. Use of a Genetic Algorithm to Optimize Wheel Profile Geometry[J].Journal of Rail and Rapid Transit, 2007, 221(4): 467-476.
[11] SANTAMARIA J, HERREROS J, VADILLO E G, et al. Design of an Optimised Wheel Profile for Rail Vehicles Operating on Two-track Gauges[J]. Vehicle System Dynamics, 2013, 51(1): 54-73.
[12] BRAGHIN F, LEWIS R, DWYER-JOYCE R S, et al. A Mathematical Model to Predict Railway Wheel Profile Evolution Due to Wear[J]. Wear, 2006, 261(11): 1253-1264.
[13] LEARY J F, HANDAL S N, RAJKUMAR B. Development of Freight Car Wheel Profiles a Case Study[J]. Wear, 1991, 144(1): 353-362.
[14] 罗仁,曾京,邬平波,戴焕云.高速列车轮轨参数对车轮踏面磨耗的影响[J]. 交通运输工程学报,2009,9(6):47-54.
LUO Ren, ZENG Jing, WU Ping-bo, et al. Influence of Wheel/Rail Parameters on Wheel Profile Wear of High-speed Train[J].Journal of Traffic and Transportation Engineering, 2009, 9(6):47-53.
[15] British Standards Institution. BS EN 13715: 2006 Railway Applications-wheelsets and Bogies-wheels-wheels Tread[S]. London: British Standards Institution, 2006.
[16] International Union of Railways. UIC Code 519 Method for Determining the Equivalent Conicity[S].1st ed. Paris: International Union of Railways, 2004.
[17] Polach O. Characteristic Parameters of Nonlinear Wheel/Rail Contact Geometry[J]. Vehicle System Dynamics, 2010, 48(S1): 19-36.
[18] British Standards Institution. BS EN 14363: 2005 Railway Applications-testing for the Acceptance of Running Characteristics of Railway Vehicles-testing of Running Behavior and Stationary Tests[S]. London: British Standards Institution, 2005.
[19] International Union of Railways. UIC Code 518 Testing and Approval of Railway Vehicles from the Point of View of Their Dynamic Behavior-safety-track Fatigue-ride Quality[S]. 3rd ed. Paris: International Union of Railways, 2005.
[20] 干锋, 戴焕云, 高浩,等. 铁道车辆不同踏面等效锥度和轮轨接触关系计算[J]. 铁道学报, 2013, 35(9): 19-24.
GAN Feng, DAI Huan-yun, GAO Hao, et al. Calculation of Equivalent Conicity and Wheel-rail Contact Relationship of Different Railway Vehicle Treads[J]. Journal of the China Railway Society, 2013, 35(9):19-24.

