高速车体结构参数对车体模态频率的影响分析
于金朋, 张卫华, 孙帮成, 黄雪飞, 张立民, 肖守讷
(1. 西南交通大学 牵引动力国家重点实验室, 四川 成都 610031;2. 唐山轨道客车有限责任公司 产品技术研究中心, 河北 唐山 063035)
随着列车速度的不断提高,车辆在运行中受到的垂向、纵向、横向和扭转载荷等随之增大;另一方面由于车辆轻量化,使车辆的固有频率降低。而线路激励频率范围随速度提高而加宽,可能导致车辆低阶固有频率处于线路激扰频率范围之内,使得车体产生较大的振动[1-3]。
车体承载能力和强度(屈服和破坏)有关,也和刚度(屈曲和共振)有关[4-5]。车体结构厚度的变化会导致刚度和质量的变化,而车体的刚度控制结构的变形(挠度)、稳定性和固有频率[6-7]。车体刚度不足不仅降低车体弯曲自振频率,使之与转向架构架自振频率接近,降低乘坐舒适度,也导致车体因振动过大而使结构局部产生较大变形影响材料疲劳寿命和列车运行品质,并很大程度上限制了车体结构承载能力的发挥[3,8-9]。日本学者[10]推导出铁道机车车辆等效弯曲刚度的解析计算方法,定性地指出了组成车体各部件对车体弯曲刚度的影响。Masamor、Takamatsu等[11]分析了轿车白车身组成部件对整车刚度的贡献情况,结果表明白车体对整车刚度的贡献达到60%以上。任万勇[12]通过模态分析优化结构设计参数,改善了转向架承载结构动态特性,提高了结构安全性。
为了避免或减少由于振动模态频率引起的各类问题的发生,需对车体结构从传统的静态设计转为车辆动态性能的动态设计[13]。合理的结构设计,将使车体具有良好的动态特性,不仅能避免与转向架构架自振频率接近,也能提高车体的弹性弯曲自振频率,从而减小振动,提高车辆的安全可靠性。
1 车体有限元模型建立及设计变量选取
1.1 车体模型
通过HYPERMESH对几何模型划分网格,车体模型(见图1)采用板壳单元SHELL63进行离散,整车总共划分为310 106个单元,551 560个节点。车体各部分的板厚根据实际参数定义为实常数,车体有限元离散模型见图1。

1.2 结构设计变量
结构参数是决定结构模态参数的主要参数,而结构模态参数是决定结构动态特性的主要参数。本文重点考虑了底架中部地板、侧墙内墙板和车顶外壁板的厚度参数对车体结构模态参数的影响,为车体结构设计优化提供了依据[14-15]。
底架结构仅考虑中部地板的内外侧地板厚度变化,简化前后的结构见图2、图3。

侧墙结构鉴于厚度关系到车体限宽,只对内壁板进行厚度变化,简化前后的模型见图4。

车顶结构鉴于车辆限界因素,只对车顶平顶部分和圆弧过渡部分进行厚度变化,简化前后的模型见图5~图7。

1.3 车体原结构模态分析
模态分析用于分析结构的固有频率和振型,也是结构动力学分析和动态设计的基础[16]。利用ANSYS中的Block Lanczos方法[17]对结构进行模态分析,提取出30 Hz以内的固有频率和振型。车体的模态阶数、固有频率和模态振型(前8阶)见表1。

表1 原车结构模态分析结果(前8阶)
2 研究方法
车体结构模态频率fi是结构设计变量(结构尺寸、几何形状、模量、密度)的函数,调整结构设计变量将导致车体模态频率的变化。为了简化计算,仅考虑车体内外侧地板厚度、侧墙平直部分厚度、侧墙与底部过度部分厚度、平顶厚度以及车顶圆弧过度部分厚度为设计变量(结构几何形状、模量、密度等为常量),它们的符号及其物理含义如下:d1、d2、d3、d4、d5、d6分别为内外侧地板厚度、侧墙平直部分厚度、侧墙与底部过渡圆弧部分厚度、平顶厚度和车顶圆弧过渡部分厚度。
车体结构模态频率与这些设计变量的关系为
(1) 车体垂弯频率f1与设计变量关系
f1=G1(d1,d2,d3,d4,d5,d6)
( 1 )
(2) 车体扭转频率f2与设计变量关系
f2=G2(d1,d2,d3,d4,d5,d6)
( 2 )
(3) 车体菱形频率f3与设计变量关系
f3=G3(d1,d2,d3,d4,d5,d6)
( 3 )
在以车体固有频率为设计指标对车体结构尺寸变量进行设计时,首先给定频率指标f1C~f3C,然后从频率方程(1)~方程(3)求解出设计变量的取值域,最后根据型材和结构特点对变量修正。
当选取车体固有频率为目标时,确定设计变量取值域(或临界方程)方法为
设给定车体固有频率
fi≥fiCi=1,2,3
( 4 )
式中:fiC是给定的频率指标。
建立误差函数
E=fi-fiC≥0i=1,2,3
( 5 )
以误差函数为目标,建立性能指标
( 6 )
约束条件d1∈{a11,a12}、d2∈{a21,a22}、…、d6∈{a61,a62}。
优化后得到d1、d2、d3、d4、d5、d6满足的临界方程
G(d1,d2,d3,d4,d5,d6)=C
( 7 )
当设计变量d1、d2、d3、d4、d5、d6在上述区域取值时,不等式( 4 )就能够满足,即车体各阶固有频率fi均不小于给定频率值fiC。
在分析时,由于多设计变量工况复杂,为计算简单起见,仅选分析单一设计变量与车体固有频率关系,即
f1=G1(di)i=1,2,3,…,6
( 8 )
f2=G2(di)i=1,2,3,…,6
( 9 )
f3=G3(di)i=1,2,3,…,6
(10)
对于实际车体情况,当给定频率指标f1C~f3C时,设计变量取值域选取过程如下:
当i=1时,即仅考虑设计变量d1变化,其余设计变量保持原设计常数;
设计变量取值域问题退化为单变量多目标约束极值优化问题,设车体固有频率与频率指标误差函数见式( 5 )。
以误差函数为性能指标函数,在设计变量的可行取值域d1∈{a11,a12}、d2∈{a21,a22}、…、d6∈{a61,a62}内,通过求解(非)线性规划或优化问题,得到满足频率指标的设计变量取值域:
d1∈{a11C,a12C}满足f1=f1C
d1∈{b11C,b12C}满足f2=f2C
d1∈{c11C,c12C}满足f3=f3C
上述3个取值集合的交集R1就是在满足频率指标条件下,设计变量d1的取值域R1,则有
R1=(a11C,a12C)∩(b11C,b12C)∩(c11C,c12C)
(11)
若为空集,则适当放宽误差条件或修改频率指标。确定d1取值域的见图8。
由图8可见,满足f1=f1C的d1∈(a11,+∞);满足f2=f2C的d1∈(b11,b12)∪(b13,+∞);满足f3=f3C的d1∈(c11,c12)。它们的实数交集R1=(c11,b12)就是设计变量d1的取值域。即当d1在实数交集R1= (c11,b12)范围取值时,可以保证车体固有频率满足频率指标要求。
当i=1,2,3,…,6时,相应的设计变量取值域计算方法同上。
3 数值计算分析
根据上述方法,分别对地板、侧墙、车顶厚度变化后的车体进行模态分析,相关计算结果及其分析如下。
3.1 地板厚度对车体模态频率的影响
计算时厚度变化量为0.2 mm,内侧地板的厚度d1变化范围为2~6 mm,外侧地板的厚度d2变化范围为3~7 mm。
(1) 内侧地板厚度与车体模态频率关系
单独变化内外侧地板厚度的情况下,通过对车体模态分析得到车体模态频率随结构尺寸变化情况,见图9。
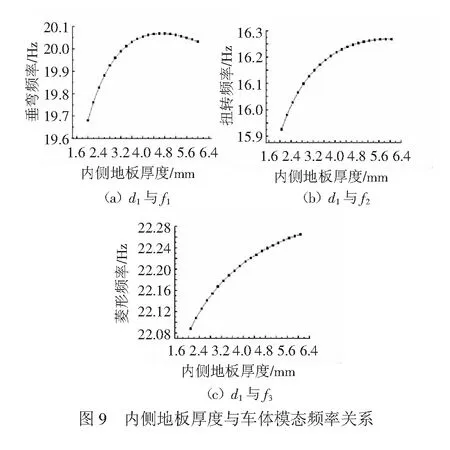
从图9(a)中可以看出:随着d1的增加,f1经历一个先增后减的过程。厚度d1增加到4.6 mm时f1取极大值(20.068 Hz)。d1大于5 mm后,随着厚度d1的增加f1开始单调下降。
从图9(b)、图9(c)中可以看出:随着d1的增加,f2、f3呈现单调递增的趋势,但是随着d1的增加,f2递增的趋势(梯度)逐渐减小。
(2) 外侧地板厚度与车体模态频率影响
单独变化外侧地板厚度的情况下,对车体进行模态分析得到车体模态频率随结构尺寸变化情况,见图10。

从图10(a)中可以看出:随着d2的增加,f1经历一个先增后减的过程。厚度d2增加到4.2 mm时f1取极大值(19.96 Hz)。d2大于4.2 mm后,随着厚度d2的增加f1开始单调下降。
从图10(b)中可以看出:随着d2的增加,f2呈现单调弱非线性递增的趋势。
从图10(c)中可以看出:随着d2的增加,f3曲线形状呈现上凸形态,d2达到5.8 mm左右时,f2有极大值(16.17 Hz)。
3.2 侧墙厚度对车体模态频率的影响
计算时厚度变化量为0.2 mm,侧墙的厚度变化范围为:d3是3~7 mm,d4是2.5~6.5 mm。单独变化侧墙厚度的情况下,通过对车体进行模态分析得到车体模态频率随结构尺寸变化情况,见图11。

从图11中可以看出:f1、f2和f3随着d3(d4)尺寸的增加,呈单调非线性增加。f1在d3(d4)尺寸增加到a+2.4 mm时有极大值(20.084 Hz),f3在d3(d4)尺寸增加到a+2.6 mm时有极大值(16.256 Hz)。
3.3 车顶厚度对车体模态频率的影响
计算时厚度的变化量为0.2 mm,车顶型材壁厚变化范围为:平顶部分d5是2~6 mm,圆弧过渡部分d6是2.5~6.6 mm。单独变化侧墙厚度的情况下,通过对车体进行模态分析,得到车体频率随结构尺寸变化情况,见图12。

从图12中可以看出:f1、f2和f3随着d5(d6)尺寸的增加,呈近似线性单调增加趋势。
3.4 不同型材厚度对车体模态频率的影响
车体模态频率随各部件型材厚度变化的模态分析结果见图13。

从图13(a)可以看出:车顶厚度~f1曲线梯度最大,即车顶厚度对f1的影响程度最大;内外侧地板厚度的增加对提高f1贡献很小。适当减小d2几乎不会影响f1;侧墙厚度的增加虽然不会明显提高f1,但是减小侧墙厚度将降低f1。
从图13(b)可以看出:车顶厚度~f2曲线梯度最大,即车顶厚度对f2的影响程度最大;内外侧地板以及侧墙厚度的增加对提高f2几乎没有显著贡献。
从图13(c)可以看出:车顶厚度~f3曲线梯度最大,即车顶厚度对f3的影响程度最大;内侧地板与侧墙对提高f3的影响没有显著贡献,外侧地板尺寸对f3的影响最小。
4 结论
通过以上研究并分析,可以得出以下初步结论:
(1) 车体垂弯频率f1均随着d1和d2结构尺寸的变化先单调增加后单调递减,只是二者拐点不一样。但若保持d2不变,单独增加d1可以提高车体垂弯频率。
(2) 车体扭转频率f2随着d1和d2的变化单调递增,且d1对f2的敏感度大于d2。
(3) 车体菱形频率f3随着d1和d2结构尺寸的变化均单调增加,且d2对其影响程度远小于d1。
(4) 型材结构尺寸对车体的固有频率f1、f2、f3有显著影响,车顶厚度对f1、f2、f3的影响大于其他尺寸。
(5) 对于给定的被研究车体,在不显著增加车体质量的前提下,可以通过调整型材部件的尺寸达到提高车体固有频率f1、f2、f3的目的。
(6) 车体固有频率f1、f2、f3与型材尺寸参数呈非线性关系。
(7) 增加侧墙厚度能提高车体弯扭频率比,增加车顶厚度能降低车体弯扭频率比,但地板厚度对弯扭频率比的影响要视其厚度而定。
为了避免或降低车体结构振动对车辆运行品质和结构安全性的影响,有必要利用模态分析理论对结构尺寸进行设计优化,确保车体结构具有良好的动态特性。以上结论可以指导车体结构动态设计优化,降低车辆振动水平,提高车辆的安全可靠性。
参考文献:
[1] 佟维.高速铝合金客车的弹性振动分析[D].大连:大连交通大学,2008:32-55.
[2] 吕永鑫.时速200公里电力机车车体结构优化设计[D].成都:西南交通大学,2008:83-92.
[3] 万波.高速列车车体主要参数关系的研究[D].成都:西南交通大学, 2009:26-50.
[4] 缪炳荣,张立民,张卫华,等. 考虑整车动力学特性的高速列车车体结构疲劳仿真[J].铁道学报,2010,32(6):101-108.
MIAO Bing-rong, ZHANG Li-min, ZHANG Wei-hua, et al. High-speed Train Carbody Structure Fatigue Simulation Based on Dynamic Characteristics of the Overall Vehilce [J]. Journal of the China Railway Society,2010,32(6):101-108.
[5] 缪炳荣,张卫华,肖守纳,等. 基于多体动力学和有限元法的车体结构疲劳寿命仿真[J].铁道学报,2007,29(4):38-42.
MIAO Bing-rong, ZHANG Wei-hua, XIAO Shou-ne, et al. Carbody Fatigue Life Simulation Based on Multibody Dynamics and FEM [J]. Journal of the China Railway Society,2007,29(4):38-42.
[6] 孙丽萍,王慧玲,朱丽,等. 封闭环结构在客车车体承载结构中的应用[J].大连铁道学院学报,2003,24(4):10-13.
SUN Li-ping, WANG Hui-ling, ZHU Li, et al. Application of Enclosed Ring in Load Bearing Structure of Passenger Car Body[J]. Joural of Dalian Railway Institute,2003,24(4):10-13.
[7] 陆娟.铝合金地铁车体静、动力学及疲劳分析[D].南京:南京工业大学,2006:29-50.
[8] 曾京,罗仁. 考虑车体弹性效应的铁道客车系统振动分析[J].铁道学报,2007,29(6):19-25.
ZENG Jing, LUO Ren. Vibration Analysis of Railway Passenger Car Systems by Considering Flexible Carbody Effect[J]. Journal of the China Railway Society, 2007,29(6):19-25.
[9] 邬平波,薛世海,杨晨辉. 基于弹性车体模型的高速客车动态响应[J].交通运输工程学报,2005,5(2):5-8.
WU Ping-bo, XUE Shi-hai, YANG Chen-hui. Dynamic Response of High-speed Passenger Car Based on Flexible Car Body Model[J]. Journal of Traffic and Transportation Engineering,2005,5(2):5-8.
[10] 菊地,龙宽.铁道车辆车体结构技术[J].国外铁道车辆,2008,45(1):9-11.
JU Di, LONG Kuan.The Carbody Structure Technology for Rolling Stock[J]. Foreign Rolling Stock,2008,45(1):9-11.
[11] TAKAMATSU M, FUJITA H, INOUE H, et al. Development of Lighter-weight, Higher-stiffness Body for New RX-7[C]. SAE Technical Paper,920244.
[12] 任万勇. 转8A货车转向架重要承载部件的模态试验与分析[J].工程力学,1999,16(S):848-851.
REN Wan-yong. Modal Test and Analysis of Important Bearing Member with the Freight Car Bogie about 8A [J].Engineering Mechanics,1999,16(S):848-851.
[13] OLE D.Dynamic Design Verfication of a Prototype Rapid Transit Using Modal Analysis[Z].Denmark:Brütie & Kjaer,1993.
[14] 卢耀辉,曾京,邬平波. 铁路客车车体轻量化问题研究[J].机械强度,2005,27(1):99-103.
LU Yao-hui, ZENG Jing, WU Ping-bo. Study on the Lightweight Body Problem of Railway Passenger Car[J]. Journal of Mechanical Strength,2005,27(1):99-103.
[15] 阳光武,肖守讷,金鼎昌. 基于弹性构架的地铁车辆动力学分析[J].中国铁道科学,2004,25(4):43-46.
YANG Guang-wu, XIAO Shou-ne, JIN Ding-chang. Dynamics Analysis of Subway Vehicle Based on Elastic Bogie[J]. China Railway Science,2004,25(4):43-46.
[16] DICKENS J M, NAKAGAWA J M, WITTBRODT M J. A Critique of Mode Acceleration and Modal Truncation Augmentation Methods for Modal Response Analysis[J]. Computers & Structures Volume,1997,62(6):985-998.
[17] NIZAR C, MATS B. Experimental and Numerical Modal Analyses of Loco Wheelset[J]. Vehicle System Dynamics,2004,41(S):597-606.

