基于改进列生成算法的高速列车开行方案优化研究

蒲 松， 吕红霞,2,3， 陈钉均,2,3， 倪少权,2,3

(1. 西南交通大学 交通运输与物流学院，四川 成都 610031；2. 西南交通大学 全国铁路列车运行图编制研发培训中心，四川 成都 610031；3. 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

高速旅客列车开行方案编制计划(High Speed Railway Passenger Train Line Planning Problems,HSRPTLP)是旅客列车运行计划的核心环节，简称开行方案。开行方案在给定路网设施的条件下，根据起讫站间客流量确定列车的运行路径、开行对数、等级与停站方案等要素，并尽可能地降低运输企业的运营成本与旅客的出行成本。

影响HSRPTLP因素众多，优化内容包括多个方面，因而建模和求解均存在一定难度。既有研究几乎均对HSRPTLP进行简化，如Bussieck、 Claessens、杜欣等[1-4]在已知列车停站方案与客流分配的基础上，建立整数规划模型优化列车运行路径、开行对数; Borndorfer、付慧伶、佟璐等[5-7]预先给定停站方案，协同优化列车运行路径与客流径路;Chang、Park等[8-9]预先确定列车的起讫站，从运输企业与旅客两方面出发，建立多目标整数规划模型确定列车开行对数、运行路径、停站方案及客流分配，并分别用于研究台湾、韩国高速列车开行方案问题;史峰等[10-11]考虑运输企业与旅客之间不对等的博弈关系(Stackelber博弈)，建立双层规划模型，但因结构较复杂，很难得到全局最优解[12]。HSRPTLP属于NP-hard问题[1-3，5]，没有有效的多项式算法，传统的分支定界算法、拉格朗日松弛算法等很难在有效时间内获得最优解。蚁群算法、模拟退火算法、遗传算法等智能算法虽然能在有效时间内获得满意解，但很难保证解的质量。

实际上，HSRPTLP模型中蕴含着多商品流结构,而列生成算法可以将具有多商品流结构的模型分解为主问题(Master Problem,MP)与其对偶问题(Dual Master Problem, DMP)，也称为子问题，有效地降低HSRPTLP的复杂度，并得到全局最优解[5,13]。但若使用标准的列生成算法求解HSRPTLP，DMP是基于客流分配的网络设计，仍然比较复杂，求解比较困难[9]。鉴于此，本文对Park等[9]的研究拓展，并考虑高速铁路线路上的列车开行方案(一般要求客流均应有直达列车提供服务，不需考虑客流换乘)。模型上，将列车运行路径与客流径路的生成合并，简化现有模型中多商品流结构，并且增加列车编组的情形；算法上，改进列生成算法，综合使用行生成与列生成策略，有效将DMP分解，弥补标准列生成算法的不足。现有研究表明[1-3,9]，系统分离方法可以通过预先分离客流，有效将多等级(不同速度)的列车开行方案转化为多个1种等级列车的开行方案。因此，只需考虑1种等级的列车开行方案。

1 建立HSRPTLP模型

1.1 基本概念

路段：相邻车站间的轨道。

铁路网：以车站为节点，路段为边构成的网络。

列车运行路径：由列车始发站、途经路段及列车终到站构成的路径。

列车非停站弧：列车直接经过车站i、j，并且在i、j间所有中间站不停站，则称弧ij为列车的非停站弧。因此，列车的所有非停站弧构成列车的停站方案，同时确定列车的运行路径。

客流OD：起讫站间客流。

列车OD：列车起讫站简称。

客流径路：旅客的乘车方案，由客流的起点站、列车的非停站弧、客流的终点站构成。

1.2 目标函数

HSRPTLP需要考虑运输企业与旅客双方的利益。因此，优化开行方案目标为

目标1 尽可能减小运输企业运营成本；

目标2 尽可能减小旅客的旅行成本。

运输企业的成本主要由列车开行的数量和列车总运行公里组成，可以分为固定成本和可变成本。其中固定成本包括铁路线路、车站等各种固定设备和动车组等移动设施的投资费用。多数研究[1-6,8-10]都对固定成本进行简化处理：由于开行方案的研究对象是列车，所以固定成本仅和列车开行数量有关，即固定成本是开行1列列车必须产生的成本。可变成本主要与列车运行里程有关，即列车每公里所产生的成本。因此，目标1可以表示为

( 1 )

由于高速旅客列车的上座率有严格的限制，拥挤费用[10]影响比较小，旅客的旅行成本主要由旅行时间刻画[1-6,8-9]。因此，目标2可以表示为

( 2 )

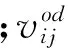
其中，tsi为列车在i站的停站时间。

1.3 约束条件

HSRPTLP的约束主要有满足客流需求与运输能力限制两大类约束。满足客流需求是开行方案编制的基本原则，运输能力主要指各路段(区间)的最大通过能力、各车站接发列车能力等，基本的约束条件表述为

客流守恒，各支客流OD途经各车站的客流量守恒，即

( 3 )

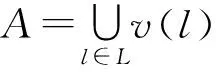
满足客流需求，经过列车l的非停站弧ij的所有客流OD不超过列车l的载客总量，即

( 4 )

最小载客量限制，经过列车l的非停站弧ij的所有客流OD不低于列车l的最小载客量，即

l∈Lij∈r(l)

( 5 )

受列车编组方式的单一性限制，旅客列车的编组是固定编组。因此，每列列车的编组模式为单组或者重联，即

( 6 )

( 7 )

式中：yl为0-1变量，表示列车的编组方式，当列车编组方式为单组时，取1，否则为0；M为一个较大的常数。

路段(区间)通过能力的限制，主要是从安全、资源限制等因素考虑，经过各路段(区间)的列车总数不超过其最大通过能力，即

( 8 )

车站接发车(包括办理始发、终到与中间停站列车业务)能力约束，即

( 9 )

(10)

式中：N为非负整数集合。

1.4 模型的复杂度分析

HSRPTLP的优化模型是多目标规划模型，而多目标规划模型将大大增加问题的复杂度。同文献[4-9]，利用权重法将多目标规划转化为单目标规划，即

(11)

HSRPTLP是NP-hard问题，假设路网是仅含n个车站的客运专线，则共有非停站弧n!条，整数变量个数为

约束条件个数为

模型的约束与变量随着路网规模的增大而呈指数规模的增长，即使是对小规模的实例，也很难在有限的时间内找到高质量的解，甚至连找到可行解都很困难。因此，根据模型特点，设计基于列生成与行生成的启发式算法。

2 列生成算法求解模型

2.1 主问题的构造

设Ω=(L,F,v(L),Cap(L))为主问题的解空间，L、F、v(L)、Cap(L)分别表示列车集合、对应列车的开行对数集合、列车的非停站弧集合及编组方式集合。因规模较大，所以在求解的过程中给出Ω的1个子集，其规模远远小于Ω，并且在每次迭代中逐渐生成。此时，主问题变为限制的主问题(Restricted Master Problem, RMP)，相应的子问题变为限制的子问题(Dual Restricted Master Problem,DRMP)。

线性规划中一般含有耦合约束与块状约束，标准列生成算法运用DW分解法分解耦合式( 8 )、式( 9 )构造RMP，其对偶问题与块状约束一起构成DRMP。DRMP为RMP提供新增列车的信息(运行路径、停站方案)，并将列车的信息以“列”的形式增加到主问题的约束中[9,13]。列车生成算法能有效的将原问题进行分解，从而减小原问题计算的复杂度，但对于HSRPTLP，DRMP仍然比较复杂[9]。因此，本文采用另一种方式生成主问题，即将所有约束(耦合约束、块状约束)均放入RMP中，则可以为DRMP提供较多的信息，从而降低DRMP求解的复杂度[5,14-16]。

设t次迭代限制主问题的解空间为Ωt=(Lt,Ft,v(L)t,Cap(L)t)，其规模远远小于Ω，只需将式( 3 )～式( 9 )中L替换为Lt，并将整数变量(式(10))松弛为连续变量，即构成限制的主问题RMP(Ωt)

RMP(Ωt)：式(11)、式( 3 )～式( 9 )

(12)

RMP(Ωt)是线性规划问题，可以用单纯形算法求解。

2.2 子问题的构造

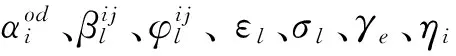
(13)

o,d∈Vi,j∈v(l)

(14)

l∈Ltij∈r(l)

(15)

l∈Ltij∈r(l)

(16)

(17)

(18)

(19)

εl≥0l∈L

(20)

σl≥0l∈L

(21)

γe≥0e∈E

(22)

ηv≥0v∈V

(23)

2.3 列生成与行生成

RMP(Ωt)中，约束( 4 )～约束( 7 )不能预先确定，则DRMP(Ωt)中含有对偶变量缺失的约束，标准的列生成算法可能在达到最优解前终止运算[14]。因此，需要在RMP(Ωt)中同时增加新的列车与相应的式( 4 )～式( 7 )，即列生成与行生成。

多数学者采用两阶段方法处理列生成与行生成问题，需要进行两阶段的反复迭代，计算比较复杂[14,16]。文献[15]采取增加虚拟路径的方法处理对偶变量缺失，避免进行两阶段的反复迭代。

根据强对偶理论可得以下定理

定理1若对所有的列车l∈L/Lt，约束(13)～约束(16)均满足，则MP达到最优解，否则，不能达到最优解。

类似于文献[15]，构造虚拟列车l*，其非停站弧集合r(l*)包括所有的非停站弧(该虚拟列车并没有实际意义，只是为了产生对偶解)，则可由r(l*)构造任意列车l∈L/Lt的非停站弧集合v(l)，从而构造Ω/Ωt内的任意解。然后，建立以下线性规划模型(Linear Programme,LP)

(24)

o,d∈Vi,j∈v(l*)ij∈r(l*)

(25)

ij∈r(l*)

(26)

ij∈r(l*)

(27)

(28)

(29)

εl*≥0

(30)

σl*≥0

(31)

(32)

(33)

根据定理1及文献[15]的讨论容易得到定理2。

定理2若LP的目标函数值为0时，MP达到最优解，否则MP不能达到最优解。

2.4 子问题的求解

当LP的目标函数值为正数时，约束(14)不被满足，即(o,d)客流间的非停站弧ij需要增加到RMP中。因此需要将含有非停站弧ij的列车l及相应的式( 4 )～式( 7 )，增加到RMP(Ωt+1)中。

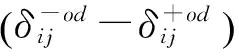
2.5 列车起讫站的调整

由2.1～2.4节，可以确定列车集合L及其非停站弧集合v(F)。实际上，并不是任意车站均可以作为列车的起讫站，列车起讫站的设置不仅需要考虑车站的客运需求，而且还需要考虑车站的动车布局、路网属性、社会属性等因素[5]。因此，可以预先确定列车的起讫站集合SF，然后将列车l∈L的运行路径延伸到最近的起讫站。该问题可以转化为含固定弧l的最短路径问题，可以用2.4的方法进行求解。

2.6 求解HSRPTLP

根据2.1～2.5节，在松弛整数式(10)的条件下，确定列车集合L及其非停站弧集合v(F)，并且得到的1个下界ZLP。然后，恢复模型的整数式(10)，以L、v(F)作为已知条件代入HSRPTLP，并运用分支定界算法得到解ZIP，ZIP不一定是他的最优解，只是他的1个上界。

将L、v(L)作为已知条件代入HSRPTLP后，其求解难度远远小于原问题的难度，可以用分支定界算法进行求解，但传统的分支定界算法耗时较长，需要对分支定界算法进行局部的改进。

在定界剪支阶段，仍采用松弛整数约束的方法定下界，并根据下界剪支。

2.7 算法的综合步骤

改进列生成算法的主要步骤如下

Step1令t=0、Lt={l0}，其中列车l0以高速线路的起点、终点为起讫站，停站方案为站站停。根据2.1节、2.2节生成RMP、DRMP，并用单纯形算法进行求解；

Step2根据2.3节构造包含所有非停站弧的虚拟列车l*，生成LP问题，并用单纯形算法进行求解，若LP问题的目标函数小于ε(ε取10-6)，则进行step4，否则进行step3；

Step4根据2.5节所述方法对列车起讫站进行调整；

Step5根据2.6节，将L、v(L)作为已知条件代入HSRPTLP，并运用改进的分支定界算法求解。

3 案例分析

以京沪高铁本线客流数据(2013-07～2013-08)为依据进行案例研究[18]。京沪高铁主要跨越23个站，由北向南各站名及序号依次为1北京南、2廊坊、3天津南、4沧州西、5德州东、6济南西、7泰安、8曲阜东、9滕州东、10枣庄、11徐州东、12宿州东、13蚌埠南、14定远、15滁州、16南京南、17镇江南、18丹阳北、19常州北、20无锡东、21苏州北、22昆山南、23上海虹桥。

现开行方案实际运行2种速度等级的列车，即G类列车(G字头列车)与D类列车(D字头列车)，鉴于系统分离法分离客流不属于本文研究的内容，且D类列车所占比例较少(约占13.8% )，为计算方便，假设仅开行G类列车。

主要参数：G类列车速度为300 km/h，停站时间6 min(含起停附加时间)，固定成本42 000元/列，可变成本150元/列·km(参考武广高铁)，单组列车定员500人，重联1 000人，列车最大席位利用率为100 %，最小席位利用率为40 %，时间价值vot为30元/h。列车的起讫站集合SF包含北京南、天津南、济南西、徐州东、南京南、上海虹桥[6-7,18]。

首先使用规划软件Cplex12.5和AMDA6处理器，频率1.5 Hz、内存4 G的个人计算机测试案例，运行2 h后未获得最优解。采用Matlab实施改进的列生成算法测试案例，其中所有线性规划问题用Cplex12.5处理，20 min得出结果，详见表1，迭代25次后达到稳定值，见图1。

表1 京沪高速本线列车开行方案结果

基于改进列生成算法解的误差率为Gap=(ZIP-ZLP)/ZLP×100%=2.13%，将计算结果与实际采用的开行方案[18]进行比较，见表2，从列车开行对数与开行区段上分析，计算结果中日开行列车52对，其中重联列车24对，单组列车28对，比实际减少4对(实际日开行56对列车，含10对D类列车)，运行区段为3个，比实际减少3个；从停站次数分析，计算结果的停站次数比实际减少95次;从上座率分析，计算结果的上座率范围为86.21%～99.75%，平均上座率为92.87%，实际上座率范围为23.10%～105.50%，平均上座率为85.00%。由此可见，本算法得到的开行方案能更好地与客流需求相吻合，并且优于实际采用的开行方案。

表2 与实际数据指标对比

4 结论

本文在Park等[9]研究基础上拓展，建立确定列车开行对数、运行区段、停站方案、编组方式的多目标规划模型，设计基于改进的列生成算法求解模型。案列分析表明，本算法能够在有效时间内获得优于实际结果的较高质量解，误差率为2.13%。

本文的研究可进一步改进：首先，高速路网比高速线路更为复杂，需要考虑客流的换乘问题，基于路网的高速列车开行方案是下一步研究的重点内容；其次，没有考虑列车频率对旅客出行的影响，只是规定列车的最小、最大席位利用率，防止模型求出的列车编组严重趋向于有利于运输企业的重联情形，一般列车开行频率越大，旅客的广义出行成本将减少，但这种关系的准确描述很难确定；最后，单层模型中客流分配与标准客流分配还存在一定偏差，不能完全反映旅客的实际选择行为。因此，单层模型中客流分配问题还需继续研究。

参考文献：

[1] BUSSIECK M R. Optimal Lines in Public Transport[D]. Germany: Technical University Braunschweig,1998:11-17.

[2] CLAESSENS M T, DIJK N M, ZWANEVELD P J . Cost Optimal Allocation of Rail Passenger Lines[J]. European Journal of Operational Research, 1998,110(3):474-489.

[3] BUSSIECK M R, KREUZER P, ZIMMERM U T. Optimal Lines for Railway Systems[J]. European Journal of Operational Research, 1997, 96(1):54-63．

[4] 杜欣，牛永涛，韩宝明，等. 基于节点重要度的客运专线旅客列车开行方案[J].北京交通大学学报，2010，34(6)：5-10.

DU Xin, NIU Yong-tao, HAN Bao-ming, et al. Train Service Planning for Passenger Dedicated Railway Line Based on Analyzing Importance of Nodes[J]. Journal of Beijing Jiaotong University, 2010, 34(6): 5-10.

[5] BORNDORFER R, GROTSCHEL M,PFETSCH M E. A Column Generation Approach to Line Planning in Public Transport[J]. Transportation Scinece, 2007, 41(1):123-132．

[6] 付慧伶，聂磊，杨浩，等.基于备选集的高速铁路列车开行方案优化方法研究[J].铁道学报，2010，32(6)：1-8.

FU Hui-ling, NIE Lei, YANG Hao, et al. Research on the Method for Optimization of Candiate Train Set Based Train Operation Plans for High Speed Railways[J]. Journal of the China Railway Society, 2010,32(6):1-8.

[7] 佟璐，聂磊，付慧伶.基于复杂列车服务网络的客流分配方法研究[J].铁道学报，2012，34(10)：7-15.

TONG Lu, NIE Lei, FU Hui-ling. Research on Passenger Flow Assignment Method Based on Complex Train Service Network[J]. Journal of the China Railway Society, 2012, 34(10): 7-15.

[8] CHANG Y H, YEH C H, SHEN C C. A Multiobjective Model for Passenger Train Services Planning: Application to Taiwan’s High-speed Rail Line[J]. Transportation Research Part B, 2000, 34(2): 91-106．

[9] PARK B H, SEO Y I, HONG S P, et al. Column Generation Approach to Line Planning with Various Halting Patterns-application to the Korean High Speed Railway[J]. Asia-pacific Journal of Operational Research, 2013, 30(4): 1-19.

[10] 史峰，邓连波，霍亮．旅客列车开行方案的双层规划模型和算法[J]．中国铁道科学，2007，28(3)：110-116.

SHI Feng, DENG Lian-bo,HUO Liang.Bi-level Programming Model and Algorithm of Passenger Train Operation Plan[J].China Railway Science, 2007,28(3):110-116.

[11] WANG L, JIA L M , QIN Y, et al. A Two-layer Optimization Model for High-speed Railway Line Planning[J]. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering), 2011,12(12):902-912.

[12] GAO Z Y , WU J J, SUN H J. Solution Algorithm for the Bi-level Discrete Network Design Problem[J]. Transportation Research Part B, 2005 , 39(7): 479-495.

[13] LUBBECKE M E, DESROSIERS J. Selected Topics in Column Generation[J]. Operations Research, 2005, 53 (6) ,1007-1023.

[14] AVELLA P, DAURIA B, SALERNO S. A LP-based Heuristic for A Time-constrained Routing Problem[J]. European Journal of Operational Research, 2006, 173(1):120-124.

[15] FEILLET D, GENDREAU M, MEDAGLIA A L, et al. A Note on Branch-and-cut-and-Price[J]. Operations Research Letters, 2010 , 38(5):346-353.

[16] MUTER I, BIRBIL S I, BULBUL K, et al. Solving A Robust Airline Crew Pairing Problem with Column Generation[J]. Computers & Operations Research, 2013, 40(11): 815-830.

[17] GOOSSENS J W, HOESEL S, KROON L. A Branch and Cut Approach for Solving Railway Line Planning Problems[J]. Transportation Scinece, 2004, 38(3):379-393.

[18] 马超.京沪高速铁路开行方案评价及优化调整方法研究[D].北京：北京交通大学，2014：36-60.