高铁车-地通信中基于速度信息的酉空时调制研究
余彩虹, 郝 莉
(西南交通大学 移动通信研究所, 四川 成都 610031)
经典空时编码技术改善了无线通信系统的系统容量和可靠性性能,作为一种高效低复杂度的多天线技术受到人们的广泛关注。历经几十年发展,空时编码具有十分成熟的理论研究成果,已被纳入最近的若干无线通信标准中[1]。然而空时编码系统要求接收端获取实时的信道状态信息,这对于高速运行的车载台,较为困难。我国正在研制的超高速铁路系统行驶目标至少为500 km/h[2],此时无线信道变化很快,信道的相干时间很短,导致信道的估计非常困难甚至无法实现。以第4代移动通信系统的FDD-LTE标准为例,尽管超高速的移动用户得以支持,但多天线系统的训练序列需要占用相干时间内的时隙数,时隙数等于发送天线数目,降低了有效的带宽利用率[3]。因此,要实现高铁车地之间的高速率高可靠性的通信,应采用不需要信道状态信息的非相干传输结构。
针对非相干多输入多输出信道,学者提出了两类空时码:酉空时码[4]和差分空时码[5]。酉空时码也称作酉空时调制,待发送的若干信息比特在发送端被映射成一个具有半酉特性的空时信号矩阵,接收端则采用非相干最大似然检测方法解调出信号。酉空时调制技术的研究成果包括星座设计[6]、接收检测[7]以及该技术的实际应用,如结合多小区合作[8]、中继系统的转发方案[9]和功率分配方案[10]等。以上研究均假设无线信道空间独立且准静态,但在高铁通信环境下假设不能成立,因为电磁波散射路径不够丰富使信道具有空间相关性,而列车的快速移动产生显著的多普勒效应又引起了信道的连续时变特性。目前关于相关性信道下酉空时调制的研究成果有限。文献[11]、[12]研究了酉空时调制技术在空间相关衰落信道下的错误性能,得出信道的空间相关性不影响酉空时调制分集增益的结论。文献[13]提出了一种空间相关快时变信道下的酉空时调制的非相干接收机,该接收机要求空时信号矩阵经符号扩展后也需符合半酉性。作为另一类非相干空时码,差分空时码的性能类似于酉空时码,不过高速列车的无线信道具有连续衰落特性,差分空时码在这种情形下将面临错误传播的问题[14]。为了改善这个问题,文献[15]提出一种利用高速列车线性移动性带来的延迟相关特性的差分空时码,它假设相邻两个空时信号矩阵的信道连续变化而同一个矩阵内信道保持不变,尚未研究同一个空时信号矩阵内的信道经历连续衰落的情况。
本文首先研究了酉空时调制在空间相关连续快时变衰落信道下的最优非相干接收机,推导出相应的成对错误概率表达式。最优非相干接收机要求知道完整的信道空间相关性信息和时间相关性信息。由于列车的运行速度对高速运行环境下车地通信的信道时间相关性特性起到最主要作用且较之信道相关性信息更易于获取,本文提出了一种简化的非相干接收方案,仅利用列车的运行速度信息代替完整信道相关性信息辅助完成接收端的接收检测过程,可有效地解调出信号。分析及仿真结果表明,本文所提的简化非相干接收机接近最优非相干接收机的性能。
1 系统模型
1.1 信号模型
考虑一个下行蜂窝网络,包含一个配置M根天线的基站和一个配置N根天线的车载台,基站天线与车载台天线之间的信道假设为平坦瑞利衰落且随时间连续变化。在时刻t,车载台第n根天线上的接收符号描述为
( 1 )
式中:stm是基站第m根天线的发送符号;htmn是基站的第m根天线到车载台的第n根天线之间的信道系数,服从0均值单位方差的复高斯分布;wtn为第n根接收天线上的加性高斯白噪声,且服从0均值单位方差的复高斯分布。将发送信号的平均功率归一化为1,即
( 2 )
在T个连续符号间隔内,定义发送信号矩阵S∈CT×M、接收信号矩阵Y∈CT×N、 在时刻t上的信道矩阵Ht∈CM×N和加性噪声矩阵W∈CT×N分别为
再定义H=[H1T…HTT]T,可将式( 1 )以矩阵形式重写成
( 3 )

( 4 )
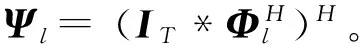
1.2 信道相关性结构
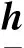
( 5 )
式中:ET是元素全为1的T×T矩阵;RM和RN分别表示发送天线和接收天线的空间相关矩阵。对于空间独立的快时变信道:(1) 根据Jakes信道模型[17],两个时间间隔为τ个符号的信道相关系数为J0(2πfdTsτ),其中J0(·)是零阶贝塞尔函数,fd是基站和车载台相对运动引起的最大多普勒频移,Ts是符号周期(最小时间单位);(2) 信道在空间上独立意味着天线对(m,n)之间的信道与其他任意天线对之间的信道相关系数为零。所以在时刻t上天线对(m,n)之间的信道增益与在时刻t+τ上天线对(m′,n′)之间的信道增益的相关系数为
( 6 )
式中:⊗是矩阵的Kronecker乘积运算;RT是一个T×T的实对称矩阵,它的第i行第j列的元素值为J0(2πfdTs|i-j|)。RT实际上表示了第m根发送天线和第n根接收天线之间的信道系数的时间相关矩阵。根据式( 5 )、式( 6 )所体现的信道相关性结构相似性,将空间相关的快时变信道的信道协方差矩阵定义为
⊗(RT⊗RM)
( 7 )
2 最优非相干接收机
( 8 )
其中
Ry|Φl=[yyH|Φl]=
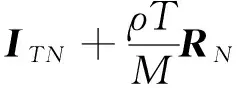
( 9 )
符号⊙是矩阵的Hadamard积运算,表示2个矩阵的对应元素相乘。式( 9 )的推导过程运用了Kronecker积与Khatri-Rao积的乘积性质[16]。根据最大似然解码准则,对p(y|Φl)进行对数运算并作最大化处理,得到空间相关快时变信道下的最优非相干接收机
(10)
最优非相干接收机需要知道完整的信道协方差矩阵,包括接收天线之间的空间相关矩阵RN,发送天线之间的空间相关矩阵RM和信道的时间相关矩阵RT。当信道条件为空间独立且准静止(即RT=ET,RM=IM和RN=IN)时,式(10)退化成
(11)
与文献[4]的式( 5 )一致。
推导最优非相干接收机的成对错误概率的理论表达式。成对错误概率是指发送Φl但接收端错判为Φl′(l′=1,2,…,L且l′≠l)的概率P(Φl′|Φl)。当码字集合L=2时,假设酉空时码的码字分别为Φ1和Φ2且被等概率发送。根据式(10),将Φ1错判成Φ2的概率P(Φ2|Φ1)可写成
(12)
φΔ(s)=
(13)
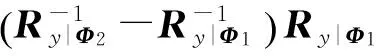
P(Φ2|Φ1)=P(Δ<0)=
(14)
式中:a是矩生成函数φΔ(s)的收敛域范围内的一个实常数。进一步使用留数定理,得到精确的成对错误概率表达式为
P(Φ2|Φ1)=
(15)
当码字集合数L大于2时,系统的码字错误概率用成对错误概率的联合界表示
(16)
3 基于移动速度信息的简化的非相干接收机
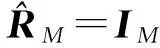

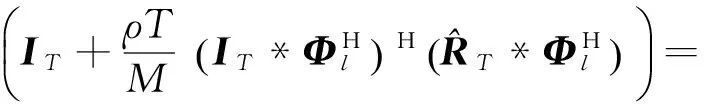

(17)
将式(17)代替式(10)中实际的协方差矩阵并忽略关于det(·)的项,得到简化的非相干接收机为
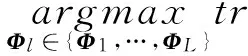
(18)
相较于最优非相干接收机,简化的非相干接收机仅需知道列车的移动速度信息即可进行信号解码。若车载台完全不知道任何信道信息,简化的非相干接收机则退化成由文献[13]提出的次优非相干接收机
(19)
经类似最优非相干接收机成对错误概率的推导过程,得到简化的非相干接收机和次优非相干接收机的成对错误概率理论表达式均形同式(15),其中简化的非相干接收机对应的rk是矩阵
(20)
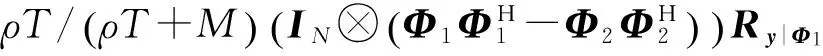
4 仿真与性能分析
对空间相关连续快时变信道下酉空时调制的最优非相干接收机、次优非相干接收机和简化的非相干接收机进行仿真与分析。参照LTE标准的系统参数,设置载波频率fc=2.5 GHz,符号间隔Ts=66 μs。设置发送天线个数M=2,接收天线数为N=1或2,同时定义相邻发送和接收天线之间的相关系数分别为rm和rn。一个空时信号块内连续符号个数T=5。酉空时调制码字集合个数假设为2,例如比特信息“1”被映射为码字矩阵Φ1,比特信息“0”被映射为码字矩阵Φ2,其中
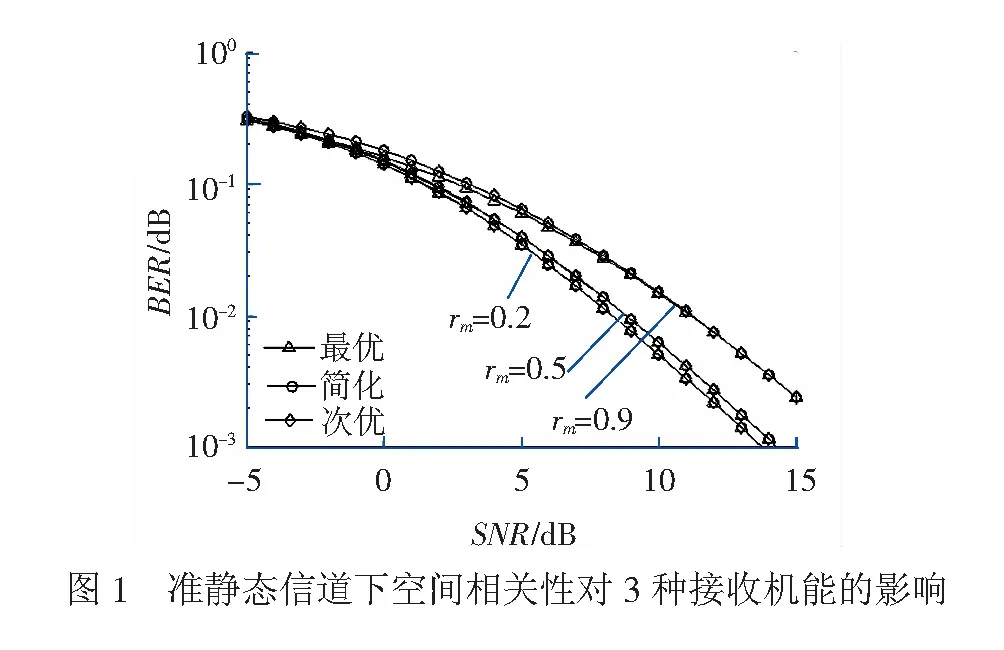
在信道仅有空间相关性的情况下,设置列车移动速度v=0和接收天线N=1,衰落信道仅具有发送空间相关性特性,显然简化接收机等价于次优接收机。不同的发送天线相关系数值对3种非相干接收机的误比特率BER性能的影响见图1。当rm由0.2提高0.5时,最优非相干接收机的误比特率变化不大;而当rm继续增大,其误比特率性能降低比较明显。此外,在高信噪比SNR情况下不使用空间相关性信息的简化接收机与使用了完整的空间相关性信息的最优接收机的误比特率曲线基本重合,说明空间相关性信息在高信噪比情况下不能改善系统的错误性能。
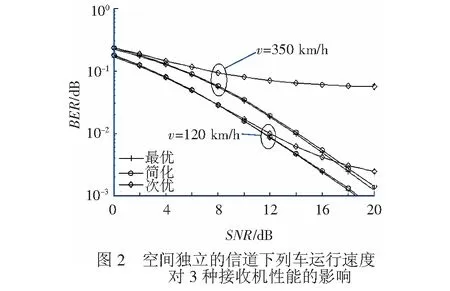
在信道为空间独立连续时变的情况下,设置rm=0和N=1,图2给出了不同列车速度情况下的3种非相干接收机的误比特率曲线。当列车速度由120 km/h提升至350 km/h时,次优接收机的错误平层随着列车速度增大而显著升高,说明列车快速运动引起的信道时间相关性对酉空时调制系统的性能有至关重要的影响。由于简化接收机利用了列车速度这个信息,它的性能在次优接收机基础上有明显改善,进而逼近最优接收机性能。
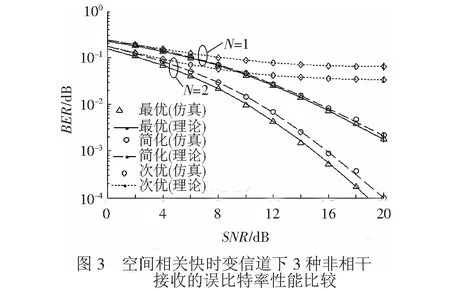
当衰落信道同时具有空间相关性和连续时变性时,3个非相干接收机的BER情况见图3。图中设置v=330 km/h和rm=0.9;当接收天线个数为2时,rn=0.8。3个接收机在不同接收天线情况下的理论与仿真曲线都十分吻合,验证了本文推导的成对错误概率表达式的正确性。简化接收机的性能略逊于最优接收机但远高于次优接收机,而且简化接收机消除了在次优接收机中由于信道时间相关性信息缺失所造成的错误平层。在接收天线数N=2情况下,简化接收机的误比特率曲线与最优接收机相比,在BER为10-4时损失了编码增益1 dB左右,但是分集增益没有减少。
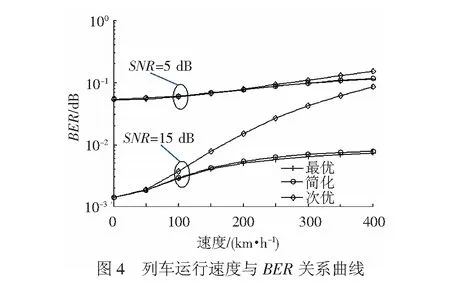
上述分析表明了当列车处于高速运行状态时,是否利用信道的时间相关性主要决定了酉空时调制的错误性能。图4给出不同列车运行速度情况下酉空时调制的3种接收机的误比特率情况。显然,列车运行速度低于50 km/h时,信道的时间相关性为系统性能的次要因素,故3种接收机误比特率差异很小;随着运行速度继续增大,信道的时间相关性逐渐变成系统性能的主要因素,次优接收机的性能劣势表现明显。本文所提的简化接收机能够保持与最优接收机相近的性能,说明了简化接收机的有效性。
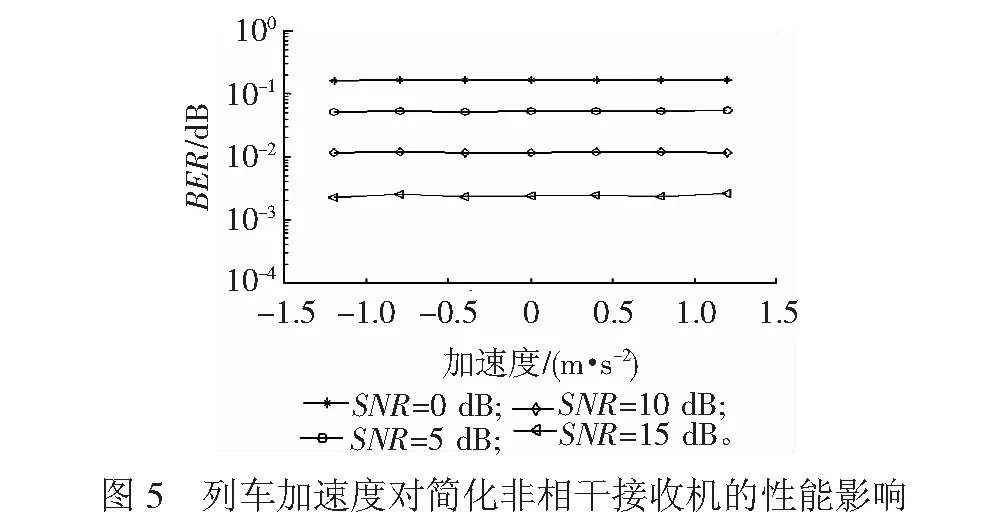
最后,分析在数据传输过程中高速列车的运行速度发生改变的情况。数据开始传输时,假设列车以初速度为v0和恒定加速度为a沿直线运行。经t个时刻,列车的瞬时速度为v(t) =v0+atTs,其中Ts是符号间隔。瞬时的最大多普勒频移可由fd(t) =v(t)fc/c=v0fc/c(1+atTs/v0)相应给出。列车运行控制系统每隔6 s更新一次列车初速度[18],在速度信息采集间隔内车载台仅知上一次采集的列车初速度v0,将其作为估计信道时间相关性的已知参数,用于后面连续若干符号的接收检测。设置列车初速度为350 km/h,列车的运动加速度对简化端非相干接收机的性能影响见图5,说明简化的非相干接收机对运动速度变化具有较强的鲁棒性。
5 结束语
在高铁车地通信环境下,无线信道同时具有空间相关性和连续时变性。本文研究了在高铁场景下酉空时调制系统的最优非相干接收机,接收端不利用信道状态信息,但需要知道信道的时间和空间相关性信息。由于高速列车的运行速度可由列车运行控制系统快速获得,且列车移动速度是决定信道的时间相关性大小的主要因素,因而提出一种仅利用速度信息的简化的非相干接收机。仿真和分析结果表明,所提的简化的非相干接收机的性能能够接近最优非相干接收机,而接收检测所需的信道相关信息易于获取,降低了系统总开销。同时,本文推导了最优接收机、简化接收机和次优接收机的理论成对错误概率表达式,仿真结果验证了理论推导的正确性。
参考文献:
[1] JAFARKHANI H. 空时编码的理论与实践[M]. 任品毅, 译. 西安: 西安交通大学出版社, 2007.
[2] 熊金超.中国开始研制时速超过500km超高速列车[N].大众科技报,2010-10-22A01.
[3] 李杰. 相干和非相干空时码的性能研究[D].上海:上海交通大学, 2007.
[4] HOCHWALD B M, MARZETTA T L. Unitary Space-time Modulation for Multiple-antenna Communications in Rayleigh Flat Fading[J]. IEEE Transactions on Information Theory, 2000, 46(2):543-564.
[5] HUGHES B L. Differential Space-time Modulation[J].IEEE Transactions on Information Theory, 2000, 46(7): 2567-2578.
[6] TAVASSOLI F, ZHOU CHI. A New Quaternary Alphabet Signal Constellation for Differential Unitary Space-time Modulation[J]. IEEE Wireless Communications Letters, 2013, 2(2): 159-162.
[7] SOLTANMOHAMMADI E, NARAGHI P M. Semi-blind Data Detection for Unitary Space-time Modulation in MIMO Communications Systems[J]. IEEE Transactions on Communications, 2013, 61(12): 5006-5015.
[8] LIU H, FAN P, HAO L. Multi-cell Cooperative Transmission Based on Unitary Space-time Modulation[J]. EURASIP Journal on Wireless Communications and Networking, 2012, 2012(1): 1-10.
[9] LIU Qian-qian,CAO Ye-wen. Soft Forwarding Technique for Unitary Space-time Modulation[J]. IET Communications, 2013, 7(16): 1810-1817.
[10] NGUYEN D H N, NGUYEN H H, HOANG D T. Power Allocation and Error Performance of Distributed Unitary Space-time Modulation in Wireless Relay Networks[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7):3333-3346.
[11] 李杰, 杨宇航. 空间衰落相关对酉空时码的影响[J]. 上海交通大学学报, 2006, 40(3):377-381.
LI Jie, YANG Yu-hang. The Impact of Spatial Fading Correlation on Unitary Space-time Code[J]. Journal of Shanghai Jiaotong University, 2006, 40(3):377-381.
[12] GUO Y, ZHU S, WANG X. Impact of Channel Correlation on Performance of Unitary Space-time Codes[J]. Chinese Journal of Electronics, 2011, 20(3):545-549.
[13] LIU D P, ZHANG Q T, CHEN Q. Structures and Performance of Noncoherent Receivers for Unitary Space-time Modulation on Correlated Fast-fading Channels[J]. IEEE Transactions on Vehicular Technology, 2004, 53(3):1116-1125.
[14] DUMAN T M, GHRAYEB A. MIMO 通信系统编码[M]. 艾渤, 唐世刚, 译. 北京: 电子工业出版社,2008.
[15] JIAO C, ZHANG Z, LI J. Delay Correlation Based Differential Space-time Modulation for high Speed Train Transmission[C]//Proceedingsof IEEE International Conference on Wireless Communications & Signal Processing (WCSP).New York:IEEE Prees,2013:1-6.
[16] 张贤达. 矩阵分析与应用[M].北京: 清华大学出版社, 2004,205-229.
[17] JAKES W C. Microwave Mobile Communications[M]. New Jersey: Wiley-IEEE Press, 1993.
[18] 张友兵, 张波, 唐涛. 列控数据传输与GSM-R越区切换发生碰撞的建模与分析[J]. 铁道学报, 2013,35(5):47-53.
ZHANG You-bing, ZHANG Bo, TANG Tao. Modeling and Analyzing of Data Transmission Colliding with the GSM-R Handover in Train Control System[J].Journal of the China Railway Society,2013,35(5):47-53.

