基于自适应LSSVM模型的动车组运行速度控制

杨 辉， 张 芳， 刘鸿恩， 付雅婷

(1. 华东交通大学 电气与电子工程学院， 江西 南昌 330013；2. 江西省先进控制与优化重点实验室, 江西 南昌 330013； 3. 湖南铁路科技职业技术学院，湖南 株洲 412000)

动车组运行过程中时变、非线性特征明显，且其处于复杂多变的运行环境，传统基于固定模型的动车组运行控制策略难以满足动车组安全、舒适、正点运行目标要求。针对动车组运行控制的研究大都忽略动车组的非线性和时变特性，通过建立动车组运行过程的线性模型或多个线性模型逼近其非线性特性。文献[1]针对高速列车自动驾驶系统提出了高速列车多模型广义预测控制方法，能较好的满足高速列车的多目标控制要求；为了适应高速列车扰动特性的变化，文献[2]在文献[1]的多模型基础上建立高速动车组的自适应模型，确保了其在动态未知故障或干扰下安全稳定运行、实现较高精度的速度跟踪控制；文献[3]依据将动车组在稳态工作点附近将其近似为线性系统的思想，采用子空间辨识方法建立动车组的动态线性模型，并同时设计预测控制器，取得了较好的控制效果；文献[4]采用T-S模型描述高速动车组的非线性和其不确定性；随着动车组运行速度的不断提高和运行环境的不确定性，其非线性时变特征愈来愈突出，线性模型已难以准确描述其运行过程。

针对动车组的运行控制，文献[5]在考虑了列车自动防护系统(ATP)的限速约束的基础上，提出了基于模型预测控制的ATO控制算法，但没有考虑列车的非线性和不确定性。针对高速列车的时变性和运行环境的不确定，文献[6]采用了基于数据的动态特征模型和黄金分割自适应控制器处理高速列车的速度和位置控制和节能等问题，并得到了良好的效果。文献[7]针对高速列车系统参数和外界组里的不确定性，基于机理模型提出了鲁棒自适应控制算法，实现了高速列车的高精度跟踪控制。

最小二乘支持向量机LSSVM (Least Squares Support Vector Machine)由Suykens[8]提出，它基于结构风险最小化,避免了局部最小值和过学习的问题保证了良好的泛化能力和更好地预测精度。以等式约束代替不等式约束,避免了求解二次规划问题,具有较好的抗噪声能力和更快的运算速度,在复杂非线性系统建模中取得较好应用成效[9]。由于LSSVM训练和拟合性能与其参数关系密切，因此采取合适的参数优化方法是建立精确模型的前提。

基于上述分析，本文提出一种基于LSSVM的动车组运行过程建模及其校正方法，据此设计动车组速度预测控制器，实现动车组运行速度高精度跟踪给定曲线。

1 动车组运行过程描述

动车组在正常运行中，假设其运行线路中的坡道很小，弯道很大，因此可以将动车组近似当作一个质点进行分析。本文仅分析动车组纵向的受力情况，其运行过程可表示为[10]

( 1 )

由式( 1 )可得到动车组运行过程的动力学模型

( 2 )

对式( 2 )进行差分变换，可描述为

y(k)=f[y(k-1),u(k-1)]

( 3 )

式中:κ2y2代表空气阻力，是速度y的非线性函数，并且随着动车组运行速度的不断增加，κ2y2所占的比例越来越大，系统非线性特性越明显，对动车组正常运行的也有越来越大的影响。

2 动车组LSSVM模型

鉴于LSSVM采用最小二乘线性系统误差平方和作为损失函数，将求解过程变成了解析一组等式方程,降低了计算的复杂度，加快了求解速度。为了得到动车组精确地动态模型，本文采用LSSVM方法建立其非线性模型。

( 4 )

约束条件为y(i)=wφ[x(i)]+b+εi。

式中:J(w,e)表示目标函数；w为权值向量；μ为正则化参数，其值的大小决定了对误差的惩罚力度；εi代表第i个样本的实际输出与模型预测输出间的误差；φ(·)是将输入变量从原始空间映射到Hilbert高维特征空间的映射函数；b为偏置量。

为了求解式( 4 )的优化问题，把约束优化问题变成无约束优化问题，建立Lagrange函数

L(w,bL,ε,αL)=J(w,ε)-

( 5 )

式中：αi∈R为拉格朗日乘子，也称作支持向量，在LSSVM的表达式中符号不受限制。

根据Karush-Kuhn-Tucher(KKT)最优化条件，分别求L(w,bL,ε,αL)关于变量w,bL,ε,αL的偏微分，并且消除变量w和ε，整理得到以下矩阵方程

( 6 )

Ψij=ψ[x(i)]ψ[x(j)]=k[x(i),x(j)]

假设HL=ΨL+μ-1IL，得

HL=

( 7 )

假设样本输出向量yL已知，解式( 6 )的矩阵方程可求出αL和bL，可得到最小二乘支持向量机的数学模型

( 8 )

由于高斯径向基函数(RBF)为非线性函数，可减少训练过程中计算的复杂性，因此本文采用RBF核函数，其表示为

( 9 )

式中：δ为核宽度;‖·‖2表示2-范数。

由以上推导过程可知，正则化参数μ和核宽度δ是得到精确LSSVM模型的重要参数，他们的选取直接影响着模型精度和泛化能力。

目前，国内外学者已经提出诸多方法用以优化正则化参数μ和核宽度δ，包括交叉验证法[12]、网格搜索法[13]、梯度优化算法[14]、遗传算法[15]和粒子群优化算法[16]等，其中，粒子群优化算法具有原理简单、易于实现、收敛速度快、设置参数少等优点而受到广泛的关注。本文采用自适应权值粒子群算法来优化选择正则化参数μ和核宽度δ。具体步骤如下：

Step1参数设置。设置粒子群的规模N,最大迭代次数M,学习因子c1和c2，最大惯性权重ωmax和最小惯性权重ωmin,粒子群的初始速度和位置分别为vsd∈RN×2和xsd∈RN×2，第i个粒子的位置为xsd(i)=[μ,δ]∈R1×2；

Step2本文选取均方根误差作为自适应权值粒子群算法的适应度函数，其具体表达式如式(10)。采用式(10)计算每个粒子当前位置的适应度值fit。取适应度值fit最小的粒子所对应的位置作为全局极值位置pg；

(10)

Step3计算每个粒子当前位置的适应度值fit。按照式(11)～式(13)进行迭代计算，更新每个粒子的速度、位置以及惯性权重

vsd(i+1)=ωvsd(i)+c1r1[pb(i)-xsd(i)]+

c2r2[pg-xsd(i)]

(11)

xsd(i+1)=vsd(i+1)+xsd(i)

(12)

(13)

式中:vsd(i)和xsd(i)分别表示第i个粒子的速度和位置；ω代表粒子的惯性权重；r1和r2是均匀分布在(0,1)区间的随机数；pb(i)为第i个粒子的个体极值位置；pg是全局极值位置；fit(i)表示第i个粒子的适应度值；fitmin代表N个粒子中适应度最小值；fitavg为N个粒子中适应度的平均值；

Step4比较每个粒子位置更新后的适应度值与其当前最优位置的适应度值，如果前者小于后者，则将更新后的位置作为此粒子的当前最优位置，反之，则不改变此粒子的当前最优位置；然后将N个粒子当前最优位置的适应度值与全局极值位置的适应度值分别作比较，选取适应度值最小的位置作为全局极值位置pg；

Step5当达到最大迭代次数或解不再变化时停止搜索。输出全局极值位置，并得到适应度值最小时的正则化参数μ和核宽度δ，即pg=[μ,δ]。否则返回step3，继续搜索。

3 自适应LSSVM模型

动车组运行环境复杂、运行过程中不确定性和突发影响因素较多，采用固定模型难以有效描述动车组复杂多变的运行特征，且基于固定模型的运行控制方法难以满足动车组运行性能要求，为此需要在动车组运行过程中对模型进行自适应校正以改善其运行控制性能。

3.1 模型校正策略

(14)

若式(14)成立，则模型不需要校正；反之，则将此新增样本纳入训练样本中，采用增量式学习方法来校正模型参数。

3.2 模型校正方法

为了避免矩阵求逆运算和解决因数据增长所带来的计算量剧增的问题，本文以已确定的模型参数通过自适应迭代计算增加一个样本后的模型校正参数。因此，得到L+1个训练样本的模型为

(15)

式中:eL+1=[1,1,…,1]T∈R(L+1)×1;IL+1为L+1维的单位矩阵;ψL∈RL×L，αL+1和bL+1分别为校正后的模型参数，假设，HL+1=ψL+1+μ-1IL+1,yL+1=[y(1),y(2),…,y(L+1)]T∈R(L+1)×1

令HL+1的逆为QL+1，即QL+1=HL+1-1。化简式(15)，可得到

(16)

(17)

由式(16)、式(17)可以看出，为了求得校正模型后的参数aL+1和bL+1就必须求出HL+1的逆QL+1。由于随着样本数据的不断加入，矩阵HL+1的维数越来越大，其求逆运算与越来越复杂。为了避免每次校正时的矩阵求逆运算，则采用递推的方法来计算矩阵QL+1。矩阵HL+1为

(18)

式中:标量

ρL+1=μ-1+k[x(L+1),x(L+1)]

βL+1={k[x(1),x(L+1)],…,k[x(L),x(L+1)]}T

根据分块矩阵以及矩阵和的求逆公式可得到QL+1的递推式

(19)

由式(19)计算得出QL+1，并代入式(16)、式(17)可得到校正后的模型参数aL+1和bL+1，从而校正动车组模型。

4 动车组速度预测控制

4.1 基于LSSVM模型的速度预测控制

针对动车组运行过程复杂多变和不确定性，给出基于LSSVM模型的动车组速度预测控制方法见图1。首先根据动车组的实际运行数据辨识得到自适应LSSVM模型。再在每个采样时刻，根据预测输出y与给定轨迹yr的偏差优化动车组的牵引/制动力u，从而实现动车组较高精度的跟踪给定轨迹和动车组安全、舒适运行。

4.2 预测模型

广义预测控制算法采用的是受控自回归积分滑动平均CARIMA (Controlled Auto-Regression Integrated Moving Average)模型。由于LSSVM模型为非线性模型，难以直接用其来设计预测控制器。为使GPC算法能应用于LSSVM模型，在每个采样周期将LSSVM模型(8)进行线性化处理[17]。假设第k个采样周期，其相应的回归量为x(k)。并在xk=(u(k-1),y(k-1))处将LSSVM模型用泰勒公式展开，得到线性模型

[x(1)-xk(1)]+…+

(20)

简化式(20)得

y(x)=C+b1x(1)+…+

bnbx(nb)-a1x(nb+1)+

…+anax(nb+na)

(21)

式中:

在LSSVM模型中，本文采用RBF核函数，则bj和aj的具体表达式为

j=1,2,…,nb

j=1,2,…,na

4.3 速度预测控制方法

为实现动车组舒适、正点运行, 采用如下二次型性能指标

(22)

式中:y(k+1)为模型超前j步的最优预测值;yr(k+1)为未来(k+j)时刻的期望输出;Δu(k+j)为控制输入的增量;N0、P、Nu分别是最小输出长度、预测长度和控制长度, 一般情况下取N0=1，并且P≥Nu.rj为控制加权系数, 约束控制量, 避免其剧烈变化。

将式(22)用矩阵形式表示为

J=E{[Y(k+j)-Yr(k+j)]T

Q[Y(k+j)-Yr(k+j)]+

ΔUT(k)RΔU(k)}

(23)

式中：

Yr(k+j)=[yr(k+1),yr(k+2),L,yr(k+P)]T

Y(k+j)=[y(k+1),y(k+2),L,y(k+P)]T

ΔU(k)=[Δu(k), Δu(k+1)L, Δu(k+Nu-1)]T

Q=[q1,q2,…,qP]为输出误差加权矩阵；R=[r1,r2,…,rN]为控制加权矩阵。

为了求解未来预测模型的输出向量Y(k+j)，现引出Diophantine方程，利用Diophantine方程的递推求解矩阵L,H,G,E，具体求解步骤见文献[1]。进而可得到

Y(k+j)=LΔU(k)+HΔU(k-j)+

GY(k)+Ev(k+j)

(24)

式中：

ΔU(k-j)=[Δu(k-1),Δu(k-2),…,Δu(k-nb)]T

为过去的控制增量；过去的输出向量为Y(k)=[y(k),y(k-1),…,y(k-na)]T；不相干随机干扰向量为v(k+j)=[v(k+1),v(k+2),…,y(k+p)]T。

式(24)等式右边的第一项为零状态预测，第2和第3项为零输入预测，这3项叠加即为最优预测估计Y×(k+j)。将式(24)代入式(23)，令dj/dΔU(k)=0可得到最优控制律ΔU(k)的表达式

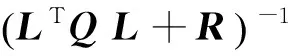
(Yr(k+j)-HΔU(k-j)-GY(k))

(25)

每个时刻经过滚动优化，从而可得第k时刻的控制力

u(k)=u(k-1)+Δu(k)=u(k-1)+

(26)

5 仿真分析

为验证本文建模与控制方法的有效性，采用运行于京沪高铁的CRH380AL型动车组为对象进行仿真实验，该型号动车组的主要参数特性见表1[18]。

表1 CRH380AL型动车组的主要参数特性

本文采集该型号动车组于徐州东—济南西区段上的实际运行数据1 500组，以其中900组数据作为建模训练数据，余下的600组数据作为测试数据验证建模效果。进一步，采用该动车组运行过程的新获得的500组数据进行模型校正。

(1)LSSVM建模比较分析

建模参数初值设置：粒子群规模N=40,最大迭代次数M=100,学习因子c1=c2=2，最大惯性权重ωmax=0.9和最小惯性权重ωmin=0.4，自变量个数D=2，正则化参数μ和核宽度δ的搜索范围分别为(0.001,8 000)和(0,5)。

首先，针对动车组900组运行数据，采用自适应粒子群优化算法确定最优的正则化参数μ=6 599.8和核宽度δ2=0.059 7，然后采用本文建模方法得到动车组LSSVM模型，其训练误差和测试误差见图2。

由图2可知，LSSVM模型输出能较高精度地拟合动车组实际运行输出，泛化能力好，其训练样本输出误差范围为(-1.262 7～1.056 8 km/h),而测试样本输出误差范围为(-1.918 2～1.836 9 km/h)。能满足CTCS-3级列控系统的定位测速误差要求，即：30 km/h以下速度误差为±2 km/h，30 km/h以上的不超过运行速度的2%[1]。

在上述LSSVM离线模型基础上，采用另外500组运行数据来校正模型参数，得到自适应LSSVM模型。设模型校正阈值x<2。为便于分析对比所提方法的有效性，分别采用自适应LSSVM模型和未校正LSSVM模型对动车组运行进行预测，对应的预测误差见图3，其对应的最大误差范围和均方根误差如表2。

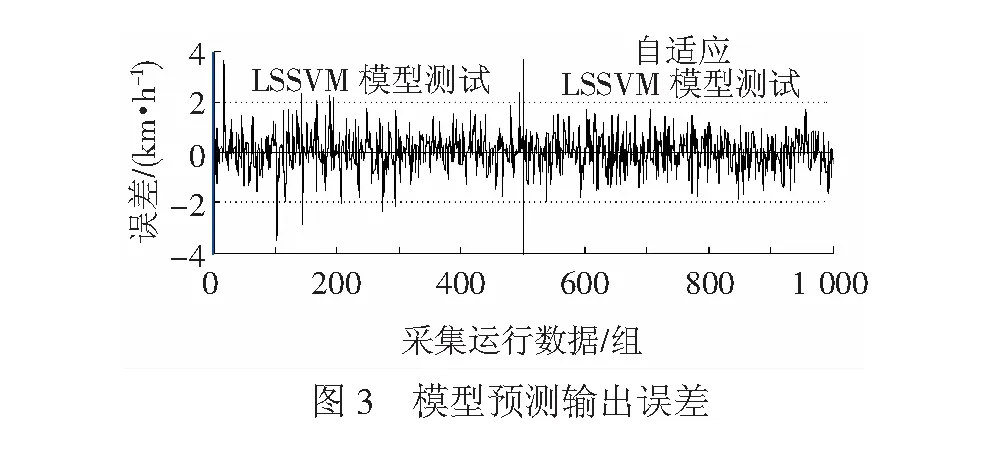
表2 模型误差比较表 km·h-1

从图3和表2可知， 未校正LSSVM模型的预测误差范围超过了2 km/h。而自适应LSSVM模型对实时数据的预测精度较高，预测误差范围均在2 km/h以内，可见自适应LSSVM模型能以较高精度预测动车组运行过程状态变化。

(2) 基于LSSVM模型的速度预测控制

为了验证自适应LSSVM模型在动车组运行速度控制的优越性。分别采用机理模型、线型多模型(文献[1])和自适应LSSVM模型设计动车组速度预测控制算法，对运行于京沪高铁徐州东—济南西区段的CRH380AL型动车组的实际运行速度进行对比跟踪控制试验。3种方法对给定速度的跟踪效果见图4，其对应的牵引力/制动力变化曲线见图5。

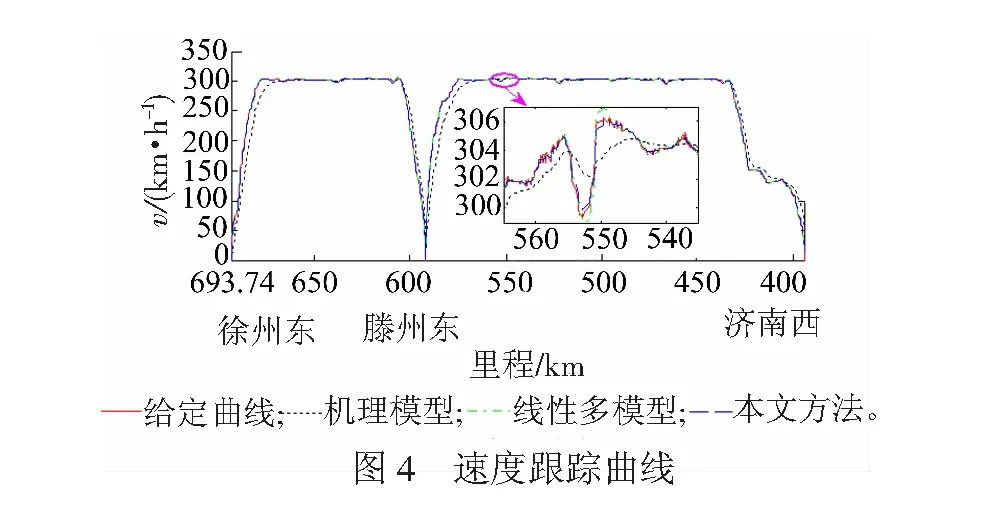
比较图4中各曲线可知，基于机理模型的预测控制方法所得速度运行曲线跟踪效果较差，尤其在动车组启动和制动阶段跟踪误差更大，对动车组安全运行带了一定的影响。本文方法在动车组牵引、恒速、惰性和制动等各个工况下均有良好的跟踪性能，保证了动车组的运行安全性和停靠准确性。而基于线性多模型的预测控制方法所得速度跟踪效果虽然比机理模型好，但在工况切换阶段与本文方法有较大差距。图5表明，基于动车组机理模型的预测控制方法所得控制力的变化范围比较大，会增大动车组能量消耗。基于线性多模型预测控制方法所得控制力在动车组运行状态变化时，其变化范围较大，影响动车组运行的舒适性。基于自适应LSSVM模型的预测控制方法得到的控制力介于上述两种方法之间，其所得动车组控制力在整个运行过程中变化平缓，过渡比较平滑，且在启动阶段满足恒牵引力和恒功率运行。在一定程度上提高了乘客的舒适性和运行平稳性。

6 结束语

为有效描述动车组运行过程的非线性特性和增强模型的适应性，提出了动车组自适应LSSVM建模方法，据此给出了基于自适应LSSVM模型的速度跟踪控制方法。通过京沪高铁徐州东—济南区间段CRH380AL型动车组运行数据的对比仿真实验分析，表明本文方法能较好地描述动车组非线性特性，具有较强的适应运行工况变化能力，并可实现动车组运行速度高精度跟踪给定速度曲线。

参考文献：

[1] 杨辉, 张坤鹏, 王昕, 等. 高速列车多模型广义预测控制方法[J].铁道学报，2011, 33(8): 80-87.

YANG Hui, ZHANG Kun-peng, WANG Xin, et al. Multiple Models Generalized Predictive Control Method of High-speed Train[J]. Journal of the China Railway Society, 2011, 33(8): 80-87.

[2] 杨辉, 张坤鹏, 王昕. 高速动车组多模型切换主动容错预测控制[J]. 控制理论与应用, 2012, 29(9): 1211-1214.

YANG Hui, ZHANG Kun-peng, WANG Xin. Multiple-models Switching Predictive Control with Active Fault Tolerance for High-speed Train[J]. Control Theory & Applications, 2012, 29(9): 1211-1214.

[3] 衷路生, 颜争, 杨辉, 等. 数据驱动的高速列车子空间预测控制[J]. 铁道学报, 2013, 35(4): 77-83.

ZHONG Lu-sheng, YAN Zheng, YANG Hui, et al. Predictive Control of High-speed Train Based on Data Driven Subspace Approach[J]. Journal of the China Railway Society, 2013, 35(4): 77-83.

[4] YANG Hui, FU Ya-ting, ZHANG Kun-peng, et al. Speed Tracking Control Using an ANFIS Model for High-speed Electric Multiple Unit[J].Control Engineering Practice, 2014, 23: 57-65.

[5] 王义惠, 罗仁士, 于振宇, 等. 考虑ATP限速的ATO控制算法研究[J]. 铁道学报, 2012, 34(5): 59-64.

WANG Yi-hui, LUO Ren-shi, YU Zheng-yu, et al. Study on ATO Control Algorithm with Consideration of ATP Speed Limits[J]. Journal of the China Railway Society, 2012, 34(5):59-64.

[6] GAO S G, QI S H, DONG H R,et al. Data-based Dynamic Characteristic Modeling and Tracking Control for High-speed Train[C]// Proceedings of IEEE 10thWorld Congress on Intelligent Control and Automation(WCICA2012).New York:IEEE Press,2002: 2913-2917.

[7] SONG Q, SONG Y D. Robust and Adaptive Control of High Speed Train Systems[C]//Proceedings of Chinese Control and Decision Conference (CCDC2010).New York:IEEE Press,2010:2469-2474.

[8] SUKKENS J A K, VANDEEALLE J. Recurrent Least Squares Support Vector Machines[J]. IEEE Transaction on Circuits & Systems-I, 2000, 47(7): 1109-1114.

[9] 宋佳, 刘胜, 李高云. 船舶航向最小二乘支持向量机内模控制[J]. 电机与控制学报, 2009, 13(1): 183-188.

SONG Jia, LIU Sheng, LI Gao-yun. LSSVM-IMC Control for Ship Course-keeping System[J]. Electric Machines and Control, 2009, 13(1): 183-188.

[10] LI X H, SONG Y D, FAN L L. Neuro-adaptive Electric Traction and Braking Control of High-speed Train[C]//Proceedings of IEEE International Conference on Service Operations and Logistics, and Informatics (IEEE/SOLI'2011).New York:IEEE Press,2011: 385-390.

[11] CHOU M, XIA X. Optimal Cruise Control of Heavy Haul Trains Equipped with Electronically Controlled Pneumatic Brake System[J]. Control Engineering Practice, 2007, 15: 511-519.

[12] 徐南, 陈逸凡, 吴彦. 基于交叉验证LSSVM的大坝监测数据处理模型[J].水利与建筑工程学报, 2013, 11(3): 67-69.

XU Nan, CHEN Yi-fan, WU Yan. Dam Monitoring Data Processing Model Based on Cross Validation LSSVM[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(3): 67-69.

[13] HUANG Q J, MAO J L, LIU Y. An Improved Grid Search Algorithm of SVR Parameters Optimization. Communication Technology (ICCT)[C]// Proceedings of 14th IEEE International Conference on Industrial Chimneys and Cooling Towers (ICCT 2012 ).New York:IEEE Press,2012:1022-1026.

[14] 陶少辉, 陈德钊, 胡望明. LSSVM过程建模中超参数选取的梯度优化算法[J].化工学报, 2007, 58(6): 1514-1517.

TAO Shao-hui, CHEN De-zhao, HU Wang-ming. Gradient Algorithm for Selecting Hyper Parameters of LSSVM in Process Modeling[J]. Journal of Chemical Industry and Engineering, 2007, 58(6): 1514-1517.

[15] 吴景龙, 杨淑霞, 刘承水. 基于遗传算法优化参数的支持向量机短期负荷预测方法[J]. 中南大学学报(自然科学版), 2009, 40(1): 180-184.

WU Jing-long, YANG Shu-xia, LIU Cheng-shui. Parameter Selection for Support Vector Machines Based on Genetic Algorithms to Short-term Power Load Forecasting[J]. Journal of Central South University:Science and Technology Edition, 2009, 40(1): 180-184.

[16] 李璇, 彭继刚, 王凯歌. 基于粒子群优化的LSSVM在模拟电路故障诊断中的应用[J]. 贵州师范大学学报(自然科学版), 2012, 30(5): 58-63.

LI Xuan, PENG Ji-gang, WANG Kai-ge.Method of LSSVM Optimized by Particle Swarm and Its Application in Fault Diagnosis of Analog Circuit[J]. Journal of Guizhou Normal University, 2012, 30(5): 58-63.

[17] LI L J, SU H Y, CHU J. Generalized Predictive Control with Online Least Squares Support Vector Machines[J]. Acta Automatica Sinica, 2007, 33(11): 1182-1188.

[18] 江靖. 新一代高速动车组牵引系统参数匹配设计与研究[J]. 机车电传动, 2011, 33(3): 9-12.

JIANG Jing. Traction System Parameter Matching Design and Research of New-generation High-speed EMUs[J].Electric Drive for Locomotives, 2011, 33(3): 9-12.