基于Wavelet-CNN的电磁炮过靶信号识别方法
田霖浩,杨 俊,郭昊琰
(中北大学 信息与通信工程学院,太原 030051)
0 引言
电磁炮[1]是通过磁场的作用来驱动电枢,与传统的火药驱动方式相比,电磁炮具有弹丸速度更快,射程更远等优势[2],因此受到了各国军事领域的极大重视。弹丸的飞行速度,作为一项重要的性能参数指标,对于整个系统的研发,生产质量检测以及弹道研究领域具有重大意义。目前针对弹丸的速度指标测试,主要有两大类测试方式:接触式(金属网靶)和非接触式,其中非接触式主要包括多普勒测速雷达[3],光幕靶[4]以及天幕靶[5]等。其中,光幕靶对于弹丸速度测试有着独特的优势,其灵敏度可调的同时,也可以保证测试的高精度[6]。
使用光幕靶进行电枢信号的提取时,由于存在强烈的火光,振动等干扰信号的存在,过靶信号会存在大量的噪声。噪声信号多为不规则的、非平稳的随机信号。在弹丸信号特征提取领域,目前研究多从频域变换的角度进行信号去噪,然后针对目标信号的峰值、脉宽、最大斜率等特征进行特征点的识别。如使用变分模态分解的方式,对弹丸过靶信号进行处理,将过靶信号分解成不同中心频率的分量,然后进行信号的重构,进而选取信号特征特征点;如基于短时傅里叶变化(STFT)和快速小波变换相结合提取信号瞬时频率的方法,该方法分段进行小波变换提取能量脊线[7],计算信号的瞬时频率并重构速度曲线。其中,小波变换具有良好的时频特性,针对电枢信号非平稳、突变特性,小波变换具有良好的识别效果。特征信号的识别准确率是计算电枢速度的重要前提,针对电枢信号,在复杂的测试环境下,发射带来的弧光信号[8]会使得激光光幕靶系统对有效信号识别时,造成严重干扰,最终导致在信号识别时出现错误识别电枢特征信号的情况,给后续的电枢速度计算带来较大的误差。当前,将卷积神经网络应用到各个不同的领域也是研究的热点。卷积神经网络[9]作为深度学习的重要组成部分,能通过“端到端的学习”,自动提取目标的深度稳定特性,在计算机视觉[10]以及自然语言处理[11]等众多领域上凸显了该算法在特征获取领域上的优势,同时卷积神经网络也在逐渐被广泛应用到特征信号识别领域。卷积神经网络对输入信号进行深层次特征提取,能实现在复杂的输入信号中提取特征信号并进行识别。如针对末敏弹目标识别问题,提出了基于卷积神经网络的末敏弹复合探测信号识别方法[12],针对毫米波辐射计、激光测距雷达和红外敏感器的复合探测信号特点,提出了单通道和多通道的信号融合方式,同时根据不同的信号融合方式构造了对应的神经网络模型,实现对末敏弹目标信号的识别;如针对滚动轴承故障判断问题,提出了卷积神经网络联合连续小波变换的方法[13],利用卷积神经网络对经离散小波变换得到的时频特征进行深层次提取,对输入信号进行分类判断,实现了对滚动轴承信号的故障判断;针对特征多样的工业故障信号,提出了通过端对端设计的离散小波变换,结合深度残差网络提取工业故障模式的深层次的特征的方法[14],实现对工业故障的分类。在特征识别提取领域,卷积神经网络对特征信号的深层次提取,使得卷积神经网络具有一定的优势。
本文针对电磁炮电枢出膛时带来的火光信号以及振动信号对目标信号带来的信号混叠干扰问题,由此引起的电枢特征信号识别错误问题,提出了一种基于小波变换联合卷积神经网络(Wavelet-CNN)的电枢信号识别方式。整个Wavelet-CNN算法模型利用小波变换对原始信号进行小波去噪,将处理过后的信号经训练好的CNN(convolutional neural network)网络结构进而提取出电枢过靶信号的特征点。实验结果表明,对比传统的小波去噪算法模型,Wavelet-CNN算法模型对电枢过靶信号的特征点拾取正确率有一定的提升,有效避免了火光信号对电枢过靶信号中特征信号提取的干扰。
1 激光光幕测速系统
激光光幕测速系统如图1所示[15],主要由光电处理电路,原向反射屏,高速信号采集模块以及上位机构成。其测速原理是基于区间测速,固定靶距s的大小,利用两个相互平行的激光光幕P1,P2,搭配上原向反射屏装置构成了一组截区装置。当弹丸穿过有效光幕区域时,会遮挡部分光线,光电探测电路将光通量的变换转化为电信号,经过光电处理模块形成多路的电枢过靶信号,由两通道的高速采集模块进行采集,并将转化为数字信号传输至上位机进行数据处理以及通道信号的显示。经上位机处理获取电枢穿过P1、P2的时刻分别为t1和t2,然后利用式(1)计算出弹丸速度v:
(1)

图1 光幕靶结构示意图
在实际复杂的测试环境中,电枢发射时伴随的强烈火光信号会使得采集到的波形会出现明显的负脉冲,同时电枢通过光幕产生的脉冲信号会叠加到负脉冲信号上,造成无法自动准确地拾取有效信号特征点的问题。为解决这一问题,本文提出一种基于小波变换和卷积神经网络结合的信号识别方式,提高电枢信号的识别准确率。
2 Wavelet-CNN基本原理
2.1 小波阈值去噪的基本原理
小波变换是傅里叶变换发展的一个重要成果,该方法是针对傅里叶变换的局限性提出的改进方法。小波变换具有多分辨率分析的特点,小波变换在时域和频域都具备良好的局部分析能力[16],是一种窗口大小固定不变但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法,小波变换的公式如下:
(2)
其中:a是比例因子,b是平移因子,f(t)为携带噪声的待处理信号,ψ(t)是小波母函数,ψ*(t)是小波母函数的共轭函数。在小波母函数的作用下,带噪信号f(t)会转换到一个包含尺度域和时间域的二维空间。小波变换中有a,b两个调节因子,通过调整b的大小来移动窗口所处的时间位置;通过调整尺度函数a来对窗口的形状和所处的频率位置进行调整,使得效果达到最佳。不同于傅里叶只能从单一维度上对信号进行分析,在小波变换中,待分析信号会被分解到时间域和频域两个域中,可以分别对相关维度进行分析。经过小波变换分解的信号会被分解为低频信号和高频信号,也称为小波的低频系数和高频系数,或者近似分量和细节分量,和原始信号进行比较,分解的两类信号中的信息长度都会被对半缩减,其中低频系数中主要包含大部分有效信息;高频信息总一般包含大量的噪声信号,需要对其进行去噪处理。原始信号经过小波变换处理之后,经过降噪处理会得到受噪声干扰程度较小的信号,然后通过小波重构算法,最终会得到和原始信号长度的相同的信号。小波去噪方法的原理在于信号和噪声在分解时,会表现出不一样的特征,所以可以根据这个特征来进行相应的去噪处理,在最大的限度上使得有效信号和噪声信号进行分离,保持信号的原始特征更加清晰,恢复原始信号的真实有效性,以此来达到去除噪声,保持纯净信号的目的。
小波变换中的多尺度分析理论是小波变换分析中的重要理论基础[17],该理论是基于图像空间分析,在不同的尺度下,图像所表现出来的特征也不相同,即在大尺度的情况下观察图像的轮廓成分,在小尺度的情况下观察图像的细节成分。那么当尺度因子从小变大的时候,就可以观察到信号在不同尺度下变现出的不同的特征。以信号三层分辨率分析为例,信号分解如图2所示。S是原始信号数据,每经过一次分解,就会分解出一个低频系数和高频系数,将分解得到的低频小波系数用Ai进行表示,分解得到的高频小波系数用Di进行表示,i=1,2,3,其中i的数值表示分解层数。由于信号的特征信号和噪声信号之前存不同的性质,随着分解层数的增加,特征信号和噪声信号会更容易区分。分解层数也是决定小波变换效果的重要因素,但当分解层数过大时,会使得得到的信息相对的减少,影响后续的信号重构而导致信号失真[18]。信号的信噪比较大时,较小的分解层数就可以去除大部分的噪声;相反,当信噪比较小时,信号中存在大量的噪声,需要选取较大的分解层数来抑制噪声。

图2 小波变换信号分解示意图
电枢的过靶信号为非平稳的突变信号,针对非平稳的信号,对原始信号进行小波变换能有效分离出原始信号的近似分量和细节分量,抑制干扰信号从而重构信号。小波阈值的去噪方法流程如图3所示。

图3 小波阈值去噪流程图
首先选取合适的小波基,根据式(2)对采集到的原始过靶信号f(t)进行小波变换,再将比例因子a和平移因子b进行离散化,获取信号的离散小波表达式;然后将f(t)经过离散小波变换得到的f(n),进行正交小波分解,得到尺度系数cj,k以及小波系数dj,k,其表达式为:
(3)
其中:c0,k为原始信号系数,h(n)为低通滤波器系数,作用于信号会得到低频的平滑信号,g(n)为高通滤波器系数,作用于信号会得到信号的细节分量;继续选取合适的阈值规则来处理小波系数,本文采用Minimax准则[19]来确定阈值的大小,选择的规则为:
(4)
式中,k为小波系数的长度,σ为噪声信号的标准差。最后根据式(5)进行信号重构,其表达式为:
(5)
2.2 CNN卷积神经网络基本原理
CNN的典型网络拓扑结构一般由输入层、卷积层、池化层、全连接层以及输出层等单层网络结构堆叠而成,每个单层网络中都具有多个独立的神经元,其中同一层网络中的神经元没有关联,相邻的网络层结构的神经元之间由于权重值和偏置值的存在而产生关联,通过多层的网络结构的参数不断迭代优化,使得神经网络具有良好的数据拟合能力,最终实现从探测信号到有效信号的良好映射。同时,CNN具有权重值共享的特性,有效地减少了网络层之间的连接数从而降低了网络结构的复杂度[20]。
卷积层的作用是通过多个卷积核提取输入的特征,也是神经网络结构中具有代表性的重要结构。卷积层利用设定好参数的卷积核与输入数据进行卷积运算,同时利用反向传播训练卷积核的权值,达到提取数据中特征信号的目的。其中,卷积核的大小和数量也是影响卷积层性能的重要因素。若卷积核太小,提取的特征会更加细致,但会丢失数据的相关性;若卷积核太大,会一定程度上保证数据的相关性,但是会造成细节数据的缺失。卷积层的计算公式如下:
(6)

池化层的作用是用于特征的选取,同时降低采样数据量进而加快模型的训练速度。目前常用的池化方法主要有最大池化、平均池化和随机池化这3种[21]。最大值池化是选取池化矩阵窗口中的最大值作为输出的特征值,其优势在于可以减小卷积层参数误差造成提取特征的估计均值偏移,保留更多的特征。平均值池化是计算池化矩阵窗口中所有特征值的平均值,将平均值作为输出的特征值,其优势在于可以避免因池化窗口受限而造成提取特征的估计值方差增大。与上述两种池化方式不同的是,随机池化方式首先根据池化窗口中的特征值与特征值总合的比值计算出概率矩阵,然后根据概率分布的大小随机输出特征值,其中概率越大的特征值,被选择的概率越高,这种方式优势在于具有随机性且可以降低网络模型的过拟合特性。为了更好的保留特征信号,本文中采用最大池化的方式,其计算公式如下:
(7)
其中:pi,m表示经过经池化后的输出;Rm表示池化区域;qi,k表示池化区域中的元素。
全连接层的主要作用是上一层网络结构输出的局部特征进行聚合,将分布式特征映射到分类器的样本标记空间,减少特征位置对分类带来的影响,也是提高神经网络模型泛化能力的重要途经。
2.3 Wavelet-CNN算法模型
基于小波变换和CNN的识别算法处理流程如图4所示。具体流程步骤如下:1)将原始信号进行小波变换,滤除低频分量和部分高频分量,重构信号;2)对于重构的批量信号划分数据集,分为训练集和测试集,然后对信号进行等长分割;3)设置神经网络的超参数,同时初始化神经网络的权重值和偏置值;4)将批量数据作为神经网络的输入,最后通过全连接层和分类层获得二进制形式的标签,神经网络前后传播计算误差,然后通过反向传播将误差回传,更新网络权重值和偏置值从而训练神经网络;5)重复第4)步,当神经网络达到设定的迭代次数后,保存训练好的神经网络,进行电枢信号的识别并输出结果。

图4 Wavelet-CNN模型结构图
若一个完整的过靶信号长度为N,等分切割为长度为L的K个区间,CNN模型将1*L的信号作为输入,输出值为0或1,其中1标定为电枢信号,那么对于整个信号长度N,则有1*K维度的输出。小波处理后的信号与输出信号的映射关系如图5所示,输出结果为1时,对于对应的神经网络的输入局部信号进行最大值检测,把局部信号的幅度最大值点作为信号特征点。

图5 序列信号映射关系图
本文的神经网络结构如图6所示。输入数据的维度为3 000*1,即图5中L取值为3 000,以保证电枢特征信号的完整性。网络结构中一共包含2个卷积层,第一层卷积使用32个卷积核对输入信号进行特征提取,第二个卷积层使用64个卷积核对网络上一层输入进行更深层次的特征提取,卷积核大小均为9*1,步长参数均为1。网络结构中还包含两个池化层,均使用最大值池化,采用此层网络的目的是降低数据维度从而加快神经网络的训练速度。最后通过两个全连接层,实现对结果的输出,两个连接层神经元个数分别为128和1。

图6 神经网络结构图
3 实验及结果分析
3.1 数据集处理
小波基的选择是影响小波变换效果的重要因素,如果信号的波形与小波基函数的波形相似,那么与小波基函数波形相似的信号将被放大,同时具有其他特征的信号将被抑制。db4小波基为正交基,具有良好的支撑性[22],同时db4小波基在时域特征上和电枢信号较为接近,故本文选取选取的小波基为db4。使用db4小波基对原始的过靶信号进行离散小波变换,分解层数为11层。原始信号如图7(a)所示,可得到不同分解尺度下的各层细节信息,如图7(b)~(l)所示。图7(b)为低频分量,不包含电枢的特征信号。电枢的特征信号主要在图7(c)~(i)所示的细节分量中。图7(j)~(l)所示的细节分量为噪声分量。
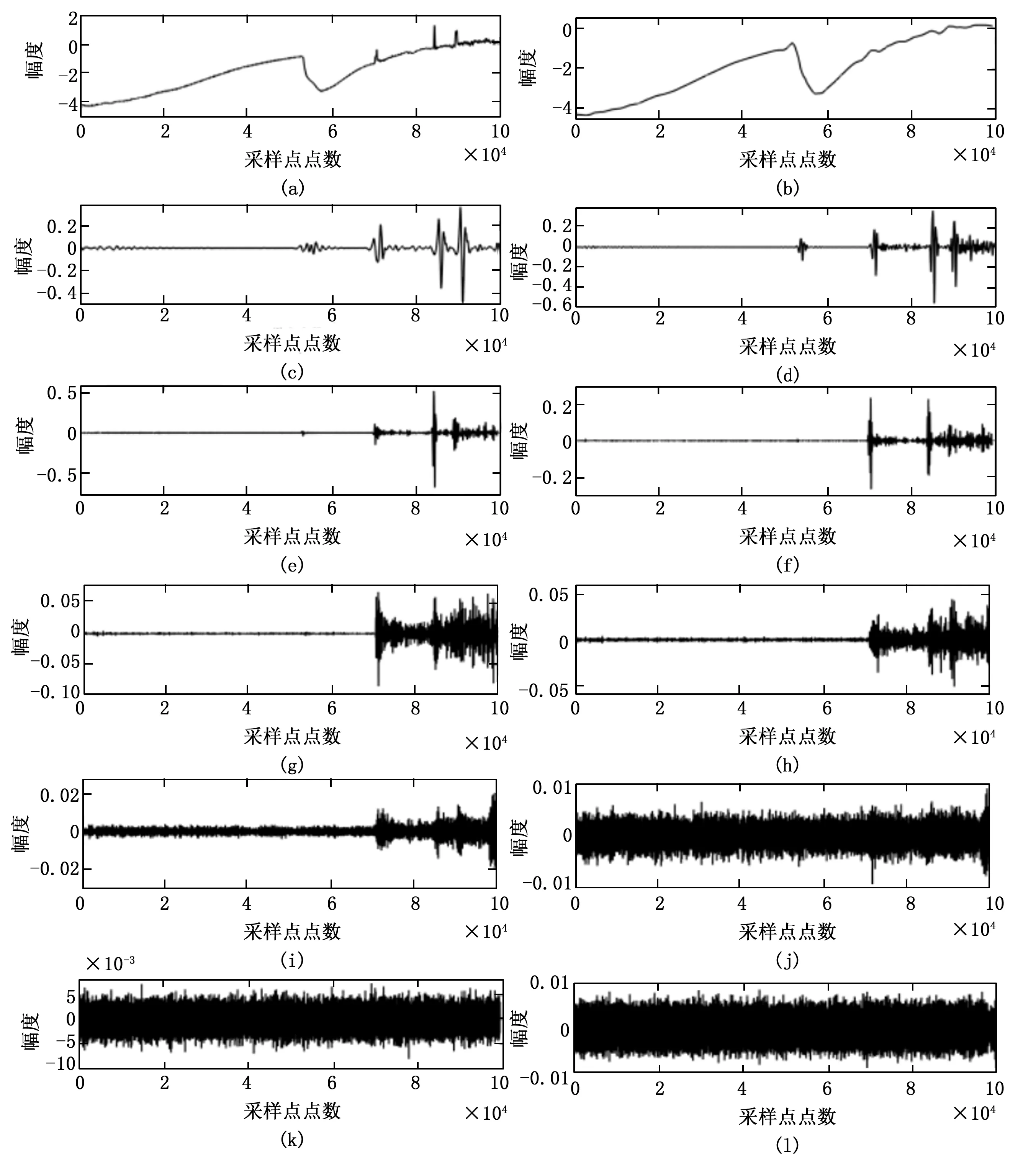
图7 小波变换各层分量示意图
将图7(b)所示的近似分量以及7(j)~(l)所示的噪声分量置0,剩余分量基于Minimax准则进行信号重构,重构后的信号如图(8)所示,从图中可知,电枢特征信号之前存在干扰信号,同时信号波形也不够平滑,不利于进行峰值检测,使得无法准确识别到信号特征点。将经过小波处理的信号数据集划为训练集和测试集,对信号进行等长度分割,长度大小为3 000个采样点,作为CNN的输入信号。
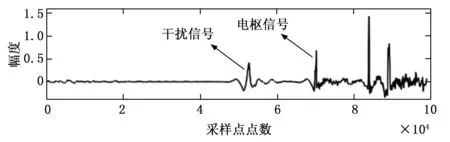
图8 重构后的信号
3.2 CNN模型训练
CNN神经网络的超参数对于神经网络的运行结果也有着重要影响[23],本文神经网络超参数的具参数设置如表1所示。其中,集成开发环境为python3.7、Pytorch和Anaconda,数据集总数为1 220,训练集和测试集划分比例为9:1。

表1 网络参数设置
对于利用神经网络处理分类问题时,评价指标主要包括以下:精确率、召回率以及F1值[24]。其中,精确率P为预测为正的样本真正为正的比例;召回率R为所有为正的样本中预测正确的比例;F1值为精确率和召回率的调和平均值,F1的求解公式如式(8)所示:
(8)
本文的神经网络的评价结果如表2所示,其中类别1为电枢信号,类别0为其他信号。根据评价评价指标实验数据可知,Wavelet-CNN模型对于有电枢信号具有一定的识别能力。
3.3 实验结论
将激光光幕测速系统测试所得的实验数据作为Wavelet-CNN模型的测试数据,其中小波变换选择db4小波基进行离散小波变换,分解层数为11,滤除低频分量后基于小波阈值去噪重构信号,然后将重构的信号作为CNN网络结构的输入并输出结果,根据映射关系确定特征点位置。图9给出了4组典型的收到强火光干扰的原始信号以及经过Wavelet-CNN模型出处理的波形效果图,上图为原始信号,下图为处理后的信号。观察图9(a),图中黑色箭头所指的波形区域为火光引起的突变信号,该算法避免了将火光引起的突变信号识别为电枢信号特征点。对于12组完整的过靶信号,共有34个特征点,使用Wavelet-CNN算法模型和传统小波阈值去噪这两种方式对电枢信号进行目标识别,实验结果如表3所示。从表3可知Wavelet-CNN降低了电枢信号的错误识别个数,对比传统小波阈值法在电枢信号特征识别正确率上提升了5.88%。

图9 波形处理结果对比图

表3 对比实验结果表
4 结束语
本文将小波变换与深度学习领域的CNN模型应用于电磁炮目标的信号识别中,提出了Wavelet-CNN算法,该算法将过靶信号进行离散小波变换,去除低频信号和部分高频噪声的同时,对剩余分量进行小波阈值去噪后重构信号。重构后的信号等分为若干局部信号作为输入信号,输入信号经过CNN网络结构判定是否为电枢特征信号。当判定为有效信号时,对局部信号进行最大值检测,依据映射关系获取信号特征点位置。实验结果表明,该方法对特征点的拾取率为82.35%,对比基于小波阈值滤波的特征点拾取率76.47%,提升了5.88%。该算法对于受到强烈火光干扰的电磁炮信号滤波识别具有一定的参考意义。但对于噪声的滤除效果以及神经网络结构的优化,算法仍需进一步研究与改进。

