基于遗传算法的动态飞机停机位分配模型研究

曾 琛，王润东

(1.中国民用航空飞行学院 新津分院，四川 新津 611431；2.中国民用航空飞行学院，四川 广汉 618307)

0 引言

民航机场是航空运输链的起点、中转点及终点，而机场停机位又作为其中生产工作的重要设施之一，是飞机在地面活动的中心[1]。因此，机场停机位分配问题是机场地面工作的核心任务，是现阶段提高航空运输效率与运输质量的一个关注热点。停机位分配问题是一个多目标、多约束条件的优化问题，复杂且多变，没有唯一的分配方案，只有在具体限定条件下的最优解。现阶段我国大多数机场主要依靠人工经验来进行机位分配，分配效率较低[2]。机场运营者为了有效地管理和利用机位等关键资源，需要采纳更加科学系统的理论可行性方案，跟上现代化民航运输业不断发展的脚步[3]。

目前利用遗传算法研究的众多问题中，主要出现了两个问题，第一个是传统的遗传算法在计算过程中，计算的执行效率十分低下，针对此问题现在主要的解决办法是通过优化计算机硬件的方法对遗传算法的计算效率进行优化，主要将算法移植到大型的服务器上计算运行；另一个问题就是遗传算法的收敛速过慢或者结果中无法找到最优解，针对此问题不少专家及研究者通常对遗传算法的因子和整体计算结构进行相应的改进。以上措施在遗传算法的实施过程中取得了显著的成效，而且改进的遗传因子和计算结构框架也慢慢的被广大学者认可，也代表着未来遗传算法的发展方向。

现阶段，国内外学者普遍认为解决机场机位资源紧缺的方法可以归纳为两种：第一种方法是通过结合自动化设备使用，制定、采纳一系列科学合理的优化措施来解决现有机位资源的分配；第二种方法从根本出发，直接新建或扩建机场来缓解现有压力，但该措施需要投入大量资源与时间成本[4]。

Abdullah Aktel(2017年)使用概率方法作为期望准则，并比较了禁忌搜索算法与模拟退火算法性能，对其他学者的研究有借鉴作用[1]。2020年，Ramazan兼顾旅客和航空公司的利益，采用模拟退火算法对模型求解，以此减少管制员进行机位分配的时间[5-6]。

2018年，马思思，唐小卫等人基于Flexsim仿真软件建立飞行区仿真模型，提升了航班运行效率，缩短了平均延误时间[7]。2020年袁媛等人综合考虑信息可视化与文献计量方法，用可视化的方式分析机位分配的进程与基础，一定程度上明确机位分配研究问题的发展趋势[8]。

1 停机位分配建模

航站楼为飞机和乘客提供服务的能力主要取决于停机位的分配是否合理，停机位分配问题考虑主要基于停机位的可用性和兼容性、其大小和容量、操作规则等[9]。在实时执行过程中，当航班时刻表的意外变化扰乱机位分配时，机位分配问题变得更加复杂。因此，机位静态分配模型应能够应对航班动态变化，并及时提供解决方案，以满足实时动态调整的需求[10]。

在第一个航班到达之前、两个后续航班起飞和到达之间以及最后一个航班起飞之后，停机位处于空闲状态。当空闲时间均匀分布在各停机位时，为实现停机位空闲时间均匀分布而引入的优化目标是按照进程时间顺序最小化空闲时间的范围和方差。

本文首先假设停机位类型相同，并且为所有航班提供相同的保障服务。对最小化停机位空闲时间范围和方差问题进行建模，使其可以通过整数松弛线性规划(LPR)方法求解。多项式算法可以将LPR解转换为停机位之间的可行分配问题解[11]。针对不同保障服务水平的停机位分配问题，本文提出了一种利用分配问题特定搜索的遗传算法，该算法与以往的单通道启发式算法相比，遗传算法在适应实时分配方面表现良好，计算出的停机位分配方案接近最优并且为机位动态变化提供了优化方案[12]。

1.1 约束条件

停机位分配问题在实际运行过程中受诸多外界客观因素的影响，存在有很强的不确定性和不稳定性，并不受预先计划分配方案的绝对控制，而是一个实时的结果，受到多方因素制约。其主要约束条件如下所示：

1)唯一性约束：一个停机位只能为一个航班提供服务。对于航班i，yik来表示航班i与停机位k之间的配置关系，yik=1当且仅当分配航班i到停机位k中，否则yik=0。该约束条件如式(1)所示：

(1)

2)独占性约束：机位被使用期间不能同时为其他航班提供服务。

3)航班优先级约束：专机优先于其他航班等约束。

4)机位安全间隔与缓冲时间约束：使用同一机位的前后两架航班之间必须产生一定安全间隔时间以此来避免潜在飞行冲突，此外相邻机位之间也需要保持一定间隔来实现航班进出的流畅性，避免飞行意外，保证飞行安全。

5)机型与机位匹配约束：机场停机位有大、中、小等级之分，匹配性发生偏差便会影响后继的飞机地面工作，降低机场运行效率。一般应尽量减少小型航班停放大型机位。

1.2 模型建立

首先对模型之中涉及到的各项数据进行说明：

1)航班数据：

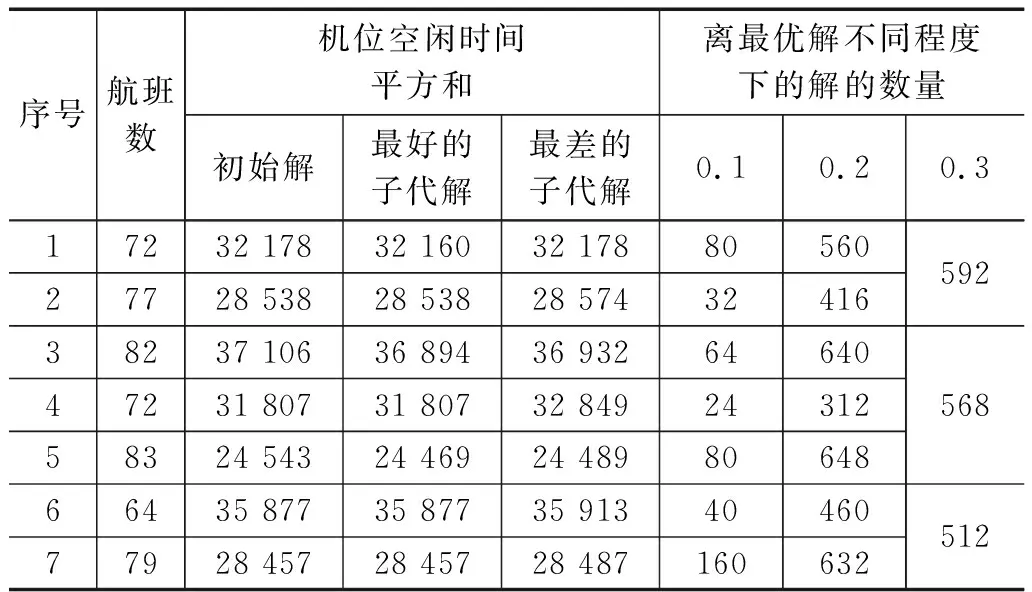
(1)设当天停放该机场的配对航班共有N对，HB为配对航班的集合，表示HB={hi|0

(2)Aij表示配对航班i计划进入停机位j的时间；

(3)Bij表示配对航班i计划离开停机位j的时间；

(4)CXi表示第i个配对航班所使用的飞机型号；

(5)Wi表示第i个配对航班的旅客数量。

2)停机位数据：

(1)设某机场共有M个停机位，其中M

(2)JKj表示第j个机位允许停靠的飞机型号集合；

(3)Dj表示第j个停机位距离航站楼的距离。

3)其他数据：

(1)yij表示航班分配结果，如果第i次航班分配到第j个机位则其值为1，否则为0；

(2)FT表示两次航班使用同一个机位的安全时间间隔；

(3)Fij表示同一个停机位上两个相邻航班之间的空闲时间。

Dj表示第j个停机位距离航站楼距离，Wi表示第i个配对航班的旅客数量，yij表示航班分配结果，那么在停机位j停放的航班人数为：

(2)

n表示机位j上分配的航班配对数量，则所有旅客登机距离表示为：

(3)

综上设旅客总登机距离最少化目标函数为f1，则：

(4)

Aij表示配对航班i计划进入停机位j的时间，Bij表示配对航班i计划离开停机位j的时间；Fij表示同一个停机位上两个相邻航班之间的空闲时间，即Fij=Aij-Bij表示时间差。设停机位空闲时间均匀目标函数为f2，则：

(5)

基于上述分析的假设条件、定义以及单个目标函数，获得机场应进行的机位分配模型：

1)模型目标函数：

(6)

2)模型约束条件：

yij∈{0，1}，∀i∈HB，∀m∈TJW

(7)

(8)

CXi∈JKj，∀(i，j)∈{(i，j)|yij=1}

(9)

Aij-Bij≥FT，∀i∈HB，∀m∈TJW，且Aij，Bij≥0

(10)

1.3 停机位空闲时间方差模型

假设N架飞机计划在某一时间段内到达机场，并且其预期落地时间Aj和地面保障时间Gj是事先已知的。航班j的起飞时间则为Dj=Aj+Gj。在一般的情况下，假设航班按照其到达时间的升序排序，则i>j，并且Ai>Aj，M个停机位中，停机位k在Bk和Fk时间节点内被占用[13]。

在静态分配阶段，尽可能均匀地利用空闲时间分配停机位，为了便于说明，规定：

Xj，k：如果航班j分配给停机位k，则等于1，否则为0；Ej，k：航班j进入停机位k的时间；Lj，k：航班j离开停机位k的时间；Sj，k：停机位k在航班j到达前的空闲时间；SN+1，k：最后一架飞机推出后停机位k的空闲时间；最后，Pj，k用于表示停机位的不同状态：如果在满足所有限制条件下，将航班j分配给停机位k，则Pj，k=1。使用模型P1优化停机位空闲时间的方差。

模型P1：

(11)

(12)

E1，k=max{A1X1，k，Bk}k=1，…，M

Ej，k=max{AjXj，k，Lj-1，k}j=2，…，N，k=1，…，M

(13)

Lj，k=Ej，k+GjXj，kj=1，…，N，k=1，…，M

(14)

S1，k=E1，k-Bkk=1，…，M

Sj，k=Ej，k-Lj-1，kj=2，…，N，k=1，…，M

(15)

SN+1，k=Fk-LN，kk=1，…，M

(16)

Xj，k=0或1j=1，…，N，k=1，…，M

(17)

Ej，k，Lj，k，Sj，k，SN+1，k≥0

j=1，…，N，k=1，…，M

(18)

1.4 停机位空闲时间范围模型

由于停机位的总可用时间和飞机的地面保障时间是恒定的，因此机位的总空闲时间恒定且与飞机的分配位置无关。因此，机位空闲时间的方差优化可用式(1)表示[14]。当Xj，k=0时，Sj，k=0称为虚拟空闲时间，此时间不会影响式(1)的大小。实际分配次数为N，非虚拟空闲时间为N+M。如果航班j刚好在航班i离开机位k后到达，即Xi，k=Xj，k=1，Li，k=Lj-1，k=Di，Ej，k=Aj，此时会出现零但非虚拟空闲时间Sj，k=Aj-Di=0。可以用合适的线性约束代替用于监控目前分配航班j之前的最后实际分配的非线性递归函数(13)。

综上，最小化空闲时间范围的优化模型P2如下：

模型P2：

minSmax-Smin

(19)

s.t.Smax≥Sj，kj=1，…，N，k=1，…，M

(20)

Smin≤Sj，k+(1-Xj，k)Zj=1，…，N，k=1，…，M

(21)

Smax，Smin≥0

(22)

Z是一个用于避免不影响最大空闲时间的虚拟空闲时间。其值代表某个机位的最大可用时间，即：

(23)

1.5 停机位空闲时间方差二元线性模型

如果航班i和j连续分配给同一个停机位，则Yi，j=1，其中i=1，…，N-1，j=i+1，…，N。由于停机位是相同的，因此上一架航班i所分配的机位对于确定是否在航班i之后立即分配航班j不再重要。对于某段时间内的首末班航班，则规定如果航班j是分配给某停机位的第一个航班，则Y0，j=1，其中j=1，…，N；如果航班i是分配给的某停机位的最后一个航班，则Yi，N+1=1其中i=1，…，N[15]。

由于停机位的服务水平是相同的，因此所有停机位在0和H时间单位之间可用，即Bk=0∀k，Fk=H∀k。如果某一飞机被连续分配到同一个停机位，假设Ii，j是航班i和j之间的空闲时间，则：

(24)

这里，Z用于表示将连续的航班i和j分配给同一个停机位是不可行的。因此，为第一次和最后一次分配的空闲时间定义I0，j和Ii，N+1：

I0，j=Ajj=1，…，N

(25)

Ii，N+1=H-Dii=1，…，N

(26)

综上，最优化空闲时间方差的纯二元线性模型P3如下：

模型P3：

(27)

(28)

(29)

(30)

(31)

(32)

Yi，j=0或1i=0，1，…，N，j=i+1，…，N+1

(33)

式(28)表明，如果所有航班都可以有可用的停机位服务，则将有N+M个空闲时间。考虑到最多有M个停机位可供使用，约束条件(29)和(30)分别保证每个停机位最多有一个航班可以是第一个到达的航班，最多一个可以是最后一个离开的航班[16]。

另一方面，式(31)和(32)表明，只有一架飞机可以分别分配在航班j之前和航班i之后。最后，使用目标函数(17)选择N+M个空闲时间最小化空闲时间的方差。模型P3具有(N+1)(N+2)/2个二元变量和2N+3个约束条件，由于模型P3具有线性目标函数，因此可以通过LPR进行优化求解，即：

模型P4：

minSmax-Smin

(34)

s.t.Smax≥Ii，jYi，ji=0，…，N，j=i+1，…，N+1

(35)

Smin≤Ii，jYi，ji=0，…，N，j=i+1，…，N+1

(36)

Smax，Smin≥0

(37)

以上讨论的优化模型针对相同保障水平的停机位，某些停机位可能不适用于某些航班，或者可能无法提供所需的保障服务。在任何情况下，当停机位不相同时，还应确定航班分配到的停机位的特征。

假设航班i和航班j被连续分配到停机位k，则Yi，j，k=1，其中i=1，…，N-1；j=i+1，…，N；k=1，…，M，因此，Y0，j，k和Yi，N+1，k为第一架和最后一架分配给停机位k的航班，则空闲时间段为II，j，k为被分给停机位k的航班i和航班j的空闲时间，因此：

(38)

同样，第一次和最后一次分配给停机位k的航班的空闲时间定义如下：

(39)

(40)

为了便于提高计算效率，纯二进制线性规划如模型P5所示。

模型P5：

(41)

(42)

(43)

(44)

(45)

i=0，…，N-1；j=i+1，…，N；k=1，…，M

(46)

Yi，j，k=0或1

i=0，…，N；j=i+1，…，N+1；k=1，…，M

(47)

目标函数(41)和(42)是P3的目标函数(27)和公式(28)的简单扩展。现在必须单独考虑每个停机位，以确定第一次分配的飞机，即约束(43)。等式(44)和(45)是等式(31)和(32)的扩展，它们分别保证在一架航班之前和之后只能分配一架航班。

2 基于遗传算法的纯二进制线性规划模型

无论飞机何时起飞或降落，停机位的状态都将发生变化，如果更新后的飞行计划未对当前机位分配产生影响，则目前的机位分配方案仍然有效。尽管模型P5的目标函数倾向于最小化中断目前机位分配方案的可能性，但产生重大飞行计划改变时，则需要重新对机位分配进行计算[17]。因此，我们需要考虑使用遗传算法(GA)对动态的机位分配进行实时计算。

我们使用N位整数字符串，其中第j位的值表示为为航班j分配的停机位的编号。

染色体如图1所示，其中3号停机位分配给航班1，6号停机位指定给航班2，M号登机门指定给航班3等等；π∈{1，2，…，M}N中可能出现一个不可行的解，对于机位分配的解，至少有一个航班违反了停机位限制条件或被分配给当已前占用的停机位[18]。即，如果存在j，对于任意i，使得Pj，π(j)=0，或者Ai≤Aj≤Di，π(i)=π(j)，在处理不可行解时，我们调整了只产生和保留可行父本和子代的措施。

2.1 适应度函数构建

根据Ii，j，k构建有效的适应度函数如下，该函数与最小化空闲时间的方差函数的目标兼容：

δo，k=δN+1，k=1 ∀k

jP=max{i：0≤i

(48)

上述函数中δjP，kδj，k用于监控连续分配到同一停机位的两个航班(jP和j)。边界条件δ0，k=δN+1，k=1，使适应度函数能够评估某段时间范围内开始和结束时的机位空闲时间。即适应度越低，机位分配方案优化效果越好。

2.2 父本选择、交叉和变异过程

选择标准的二进制联赛选择算法进行父本选择。首先将整体形成两个父本群体，每个群体由两个以相同概率随机抽取的个体组成。为了防止高度独立的个体主导选择的过程，通过允许多样性并控制收敛速度的方式减小选择压力。从两个群体池里分别选择两个最适合的个体作为父本。不仅每个群体池中的个体数量增多会增加选择更多合适个体的机会，而且二进制的选择方法效率更高[19]。

以下交叉方法适用于从双亲中产生一个子代。在1和N-1之间选择一个随机长度L。然后从第一个父代复制第一个L染色体，从第二个父代复制最后一个N-L染色体，生成一个子代。交叉后，如果新生成的解不可行，则对其执行变异过程[20]。在遗传算法的原始规则中，变异算子用于引入多样性，但在这里它用于修复染色体。导致不可行性的第一条染色体从其当前值突变[21]。在1和M之间均匀生成的随机数确定所选染色体的新值。初步实验表明，较高的突变率不会增加修改不可行方案的概率。因此，选择较小的变异率(每串最大进行M次试验)，以减小此运算过程对总运行时间的影响。

初始种群是随机生成的，其大小由分配问题的参数确定，即S=NM。对于所考虑字符串的第j位数字，随机分配一个可行的解。当目前部分解不能形成可行的完整解时，就会丢弃该部分解并启动新字符串重新计算。如果初始种群由可行解和不同的父本构建，遗传过程(交叉和突变)将继续进行，直到生成250NM的非重复子代。稳态替换方法用于消除适应度值最高的个体，并保持种群的大小不变[22]。

3 基于遗传算法的机位分配模拟仿真

3.1 模型性能测试

假设在时间单位为5分钟，飞机进入停机位的时间均匀地在15到36个时间单位之间变化。设有小型停机位5个；中型停机位10个；大型停机位20个。每个停机位的平均服务的航班数为5.15架次。小型、中型和大型机位的平均飞机停靠次数分别为26.125次、52.25次和105.417次。3种类型的机位总体平均利用率分别为45.725%、66.548%和88.871%。

首先，我们假设所有停机位类型相同，并且可以应用模型P3分配计划航班。根据设定给出了机位分配问题的变量和约束条件的数量、迭代次数和总计算时间以及优化方案的目标值(平方和、方差和空闲时间范围)。从结构上看，变量和约束条件的数量主要取决于航班和停机位的数量。

表1显示，单纯形迭代的次数随着停机位利用率的增加而减少。在所有问题中，ANOVA的F检验表明具有5%显著性水平的利用率水平具有显著影响，即F0.05，2，21=3.47。对于具有较小P值的中型停机位和大型停机位分配问题，其影响变得更加显著，即利用率水平显著，显著性水平为1%，F0.01，2，21=5.78。

表1 不同服务水平停机位的机位分配模型性测试性能结果

3.2 仿真结果

最后，使用真实数据评估该基于遗传算法的机位分配方案，对应于四川绵阳南郊机场2020年8月国内航班机位的一周运行数据。日常维护工作表和停机位停机位时刻表用于提取飞行时刻表、地面指挥员的初始分配和实时运行期间的最终机位分配。管制员在初始阶段主要考虑飞机尺寸、维修要求和飞机推出滑行等因素，例如，在航站楼的8个停机位中，停机位1和2不能用于宽体飞机(A330、B747和B777等)。每架飞机也有不同的地面保障要求。例如，B747飞机起飞前至少需要75分钟，抵达后至少需要60分钟，而B737飞机分别需要45分钟和30分钟。与此同时，一架飞机可能从前天起一直停留，地面停留时间超过三小时。指挥员则须考虑将这种类型的飞机安排到一个偏远机位。根据实际实现的飞机到达和起飞时间，管制员可以通过评估滑行道拥堵和远程停机位的使用来修改初始分配。

在7天的运行期间，四川绵阳南郊机场每天的航班数分别为72、77、82、72、83、64和79班。在静态阶段，第一到第七天必须分别将6架、8架、11架、5架、6架、3架和7架飞机分配到偏远机位，并在实时操作期间将6架，5架、六架、3、3架、2架和3架飞机从近机位推出到远机位。

我们使用相同的飞行计划来准备初始分配，然后结合实际(实现的)飞行计划来评估解决方案的鲁棒性。如果任务的空闲时间不足以吸收飞行计划中的变化，则假设相应的飞机按照目前的做法被拖到偏远机位。首先，遗传算法执行较高的运算效率，平均需要96秒(范围为57～143秒)的CPU运算来生成平均大小为594个不同解的总体。如表2所示。在最坏的情况下，计算出来的分配解离最优性只有0.2%。

表2 基于遗传算法的机位分配在仿真模拟情况下的性能表现

与目前七天实际的机位分配做法相比，在实际实施期间，共有四架飞机最初被分配到远机位，共有五架飞机被拖曳。相应地，使用最佳遗传算法给出的机位分配解决方案，静态阶段的平均改善率为92.15%，动态阶段的改善率为78.57%。

4 结束语

民航业的不断发展进步，有关机位分配问题的研究不断受到重视。一个机场若不重视机位资源的有效合理安排，那么其发展会从根本上受到制约，更不必谈到实现“四型”机场的目标。本文主要针对民航运输机场中的停机位资源分配问题进行研究，在对国内外相关机位分配研究的分析基础之上确立本文的模型，并且采用遗传算法来实现该模型的求解。提出了非线性数学模型以提供鲁棒性更高的飞机停机位分配模型，使停机位的空闲时间分布最小。本文提出了一个具有决策变量的框架将非线性二元模型转换为具有最小空闲时间范围或方差的等价线性二元模型。与四川绵阳南郊机场实际的机位分配方案相比，静态和动态阶段的平均改善率分别为92.15%和78.57%。

首先，具有相同服务水平的停机位分配模型可以直接用于实践。一些机场的停机位可以分组在一起，这样一个大的分配问题就可以分解成具有“相同属性停机位”的小分配问题。其次，遗传算法可以非常高效地为停机位分配问题提供实时响应计算。当航班时刻表的重大变化打乱了初始分配方案时，遗传算法可快速的计算出接近最优的替代分配方案。最后，遗传算法可以与机位分配专家系统集成，以满足人与人之间的系统交互，跨航空公司相关功能的标准化数据库以及用于优化的模型和程序。规划和运行环境之间的联系将为维护停机位分配和航班时刻表提供一个高效的系统。