临近空间高速飞行器微量气动力试验及计算
李俊红,靳旭红,3,,刘春风,苗文博,程晓丽
1.中国航天空气动力技术研究院,北京 100074
2.中国航天科技集团有限公司 航天飞行器气动热防护实验室,北京 100074
3.清华大学 航天航空学院,北京 100084
以全球快速到达为主要目标的临近空间高超声速飞行器可分为两类[1]:一类是吸气式动力巡航高超声速飞行器,以美国Hyper-X 计划中X-43 系 列 飞 行 器[2-6]和HyTech 计 划 中 使 用 的X-51 系列飞行器[7-9]为代表;另一类是无动力滑翔式高超声速飞行器,以美国FALCON(Force Application and Launcn from the CONtinential)计划中的HTV(Hypersonic Technology Vehicle)系列飞行器[10-12]为代表。
临近空间是指海拔高度在20~100 km 的空域[13],该空间高超声速飞行器的主要特征:在临近空间的飞行时间为几百至上千秒、飞行距离几百至上万千米[9],飞行高度跨越不同区域,从低空域的连续流区到高空的滑移流-甚至过渡流区[12]。对于这类飞行器,其气动布局设计受到诸多方面的要求与约束限制,如飞行参数范围广、技术指标高、飞行稳定性和操纵性的考虑、高超声速条件下防隔热能力、低空大动压飞行时舵面铰链力矩等[14]。相对于一般低空域的航空飞行器而言,临近空间高超声速飞行器气动布局的形式和气动设计所受的限制更加严格,对气动误差的容忍能力也相对较弱,准确的飞行器气动力热特性预测是关键,因此“精细”的气动设计必须予以重视[15],应发展准确的试验技术和并建立精细的计算方法,实现试验测量和数值计算的相互校验。
与低空域的航空飞行器类似,临近空间高超声速飞行器跨流域飞行时气动力也影响实际飞行轨道,须在设计初始阶段开展预测进行准确控制[6]。由于高空域的空气稀薄,作用于飞行器上的气动力呈几何量级递减,相同量级的气动力预测偏差对跨流域飞行器的影响更大,这对跨流域的气动力精确预测提出了更为迫切的需求[12]。
在高超声速临近空间跨流域巡航飞行段,飞行高度高、速度快、雷诺数小、黏性与黏性干扰的影响显著;同时存在高温真实气体及局部稀薄流效应的影响[13]。目前,针对此类诸多物理化学效应导致的复杂流动问题机理认识及模拟都非常有限[16],这为新型航天器的总体设计和精确控制带来诸多困难。要解决物理化学效应影响下的流动问题,需采用数值模拟和风洞试验双重手段开展流动机理和气动力热特性的研究[1]。由于风洞试验测量难度大和成本高,当前绝大多数高超声速跨流域气动研究都采用纯数值计算手段,缺乏必要的风洞试验验证[9]。
本文研究团队[17-19]对跨流域复杂多物理效应预测模型、计算方法和试验测量手段进行了研究,针对高超声速飞行器在跨流域环境中气动力准确预测的需求,研制了微量天平测力系统,采用钝锥和三角翼升力体2 个标模外形进行了气动力测量试验,并与数值计算结果相互验证。
1 临近空间跨流域微量气动力试验
临近空间跨流域风洞模拟高度在60~100 km,试验气流密度较低,由于存在黏性效应,喷管的边界层很厚,即实际的有效试验区域较小,大多数试验模型尺寸较小,低密度的气流作用在小尺寸模型上,模型的空气动力载荷比常规高超声速风洞小2 个量级以上,单位为g。研制如此微量级的六分量天平是实现低密度风洞气动力测量的关键。
微量天平设计的关键技术是天平结构设计、静态校准等。针对应变式微量天平,采用多分量优化手段开展结构设计,微量天平的校准将以高可靠性为第一原则,基于重力单向加载实现。针对跨流域环境的气动力测量需求,研制了微量天平测量系统,实现了微量天平结构设计和静态校准[20]。设计的微量天平如图1 所示。

图1 微量天平外观结构Fig.1 Appearance and structure of microbalance
基于上述设计的微量天平,针对2 种外形简单钝锥和复杂升力体外形(三角翼)开展了微量气动力测力试验研究。简单钝锥试验用于验证微量天平在风洞跨流域试验条件下的性能,重点考察微量天平的试验重复性精度;复杂升力体试验用于证明微量天平对跨流域试验条件下复杂外形微量气动力的测量能力。微量天平测力试验在中国航天空气动力技术研究院的高超声速FD-16 风洞[21]进行。
1.1 简单钝锥外形
钝锥试验模型分为圆锥和支杆2 个部件,天平设置隔热罩,支杆通过设计转接段,连接至FD-16 风洞已有的接口上。试验方案如图2 所示,钝锥外形在风洞中安装如图3 所示。圆锥尺寸:头部半径R为5.715 mm,半锥角为9°,底部直径D为38.1 mm(对应模型长度L为86 mm);支杆尺寸:长度200 mm,直径17 mm。
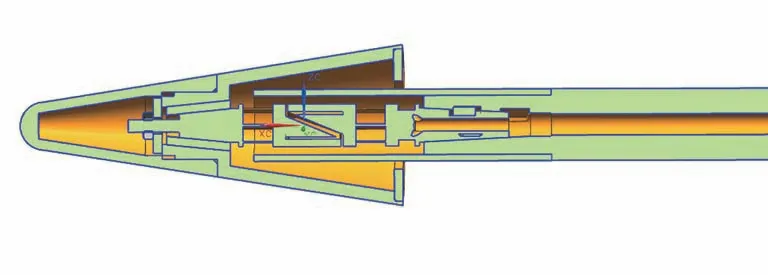
图2 钝锥外形试验方案图Fig.2 Schematic diagram of experimental blunt cone

图3 钝锥外形在风洞的安装Fig.3 Installation of blunt cone in wind tunnel
钝锥重复试验共进行3 次,试验条件如表1所示。表中,Ma为来流马赫数,P0为来流总压,q为来流动压,T0为来流总温,Re为单位雷诺数,攻角α=-4°,-2°,0°,2°,4°。在单次试验中,每个攻角停留时间2 s,在2 s 内数据采集系统一直以1 200 Hz 的采样频率采集天平信号。
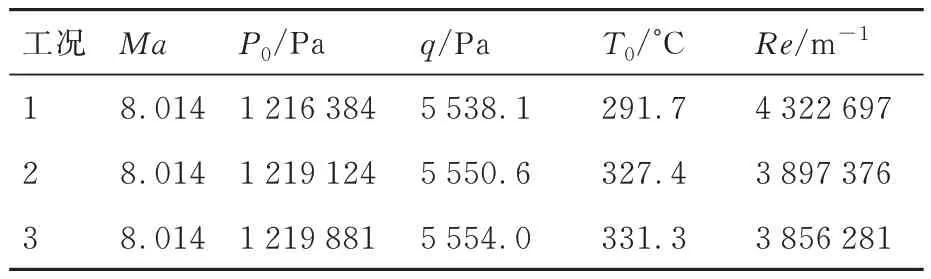
表1 钝锥外形3 次试验条件Table 1 Three test conditions of blunt cone
简单外形钝锥在3 次重复试验中的试验结果如表2 所示。其中,参考长度Lr=0.09 m,参考面积Sr=0.001 14 m2,力矩参考点为钝锥头部顶点,即坐标原点(0,0,0),CN为法向力系数,CA为轴向力系数,Cmz为z向力矩系数,且定义钝锥低头为正。具体坐标系如图4 所示。
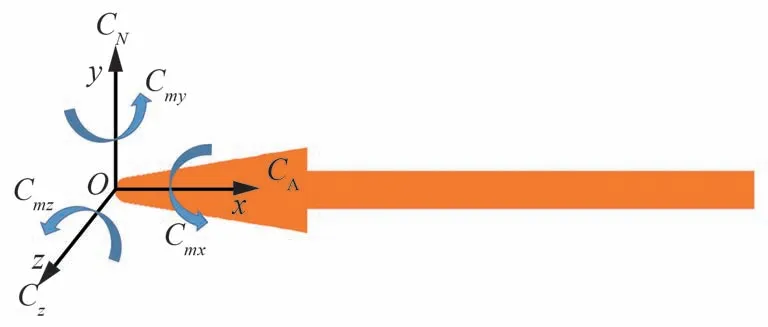
图4 圆锥坐标系定义及气动力系数示意图Fig.4 Diagram of cone coordinate system definition and aerodynamic coefficient diagram
由表2 可知,在钝锥试验中,随着超声速来流攻角由-4°转为4°,钝锥法向力由y轴负向变为正向,轴向力先减小后增大,俯仰力矩绝对值先减小后增加,即钝锥由低头力矩转为抬头力矩。
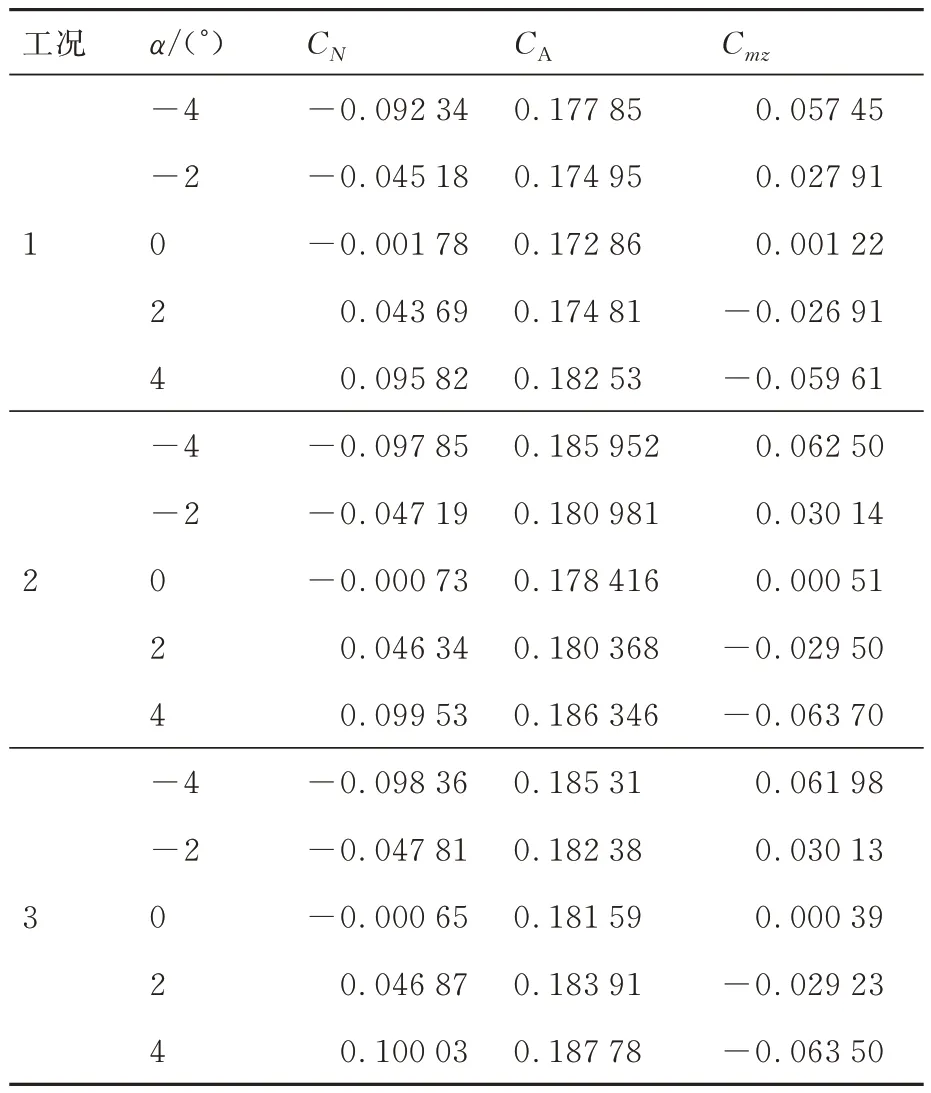
表2 钝锥微量气动力3 次重复试验结果Table 2 Three test results of blunt cone micro aerodynamics
计算得到CN、CA的试验标准偏差如表3 所示,可以看出,在不同攻角下,CN的重复性偏差最大为3.6%,CA的重复性偏差最大为4.8%。
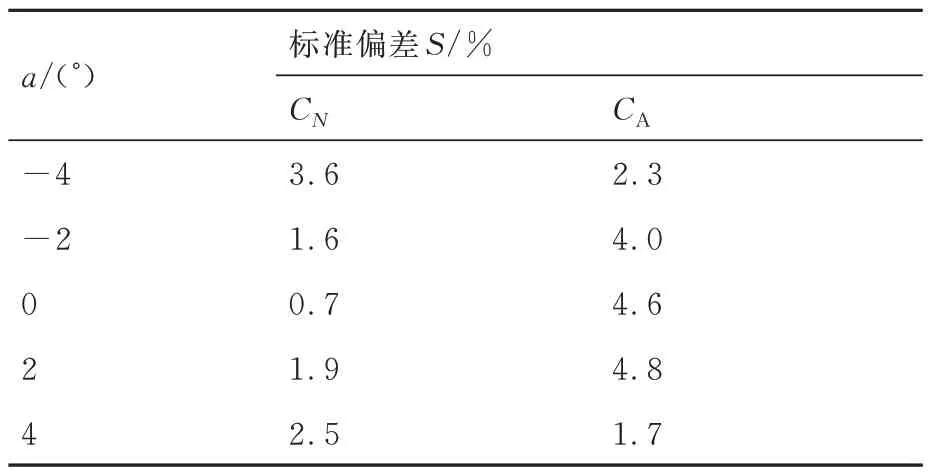
表3 钝锥3 次重复试验标准偏差Table 3 Standard deviations of three tests of blunt cone
1.2 复杂升力体外形
复杂升力体(三角翼)的外形结构如图5 所示,全长200 mm。该外形的试验方案设计如图6所示,为升力体外形分为前后两段,后段连接天平,具体尺寸如图7 所示。
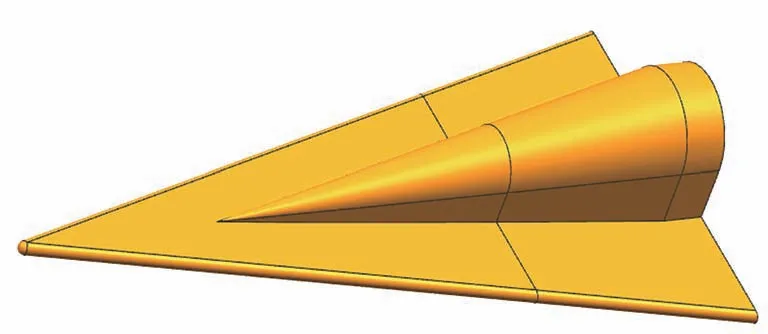
图5 三角翼升力体外形Fig.5 Lift body shape of delta wing
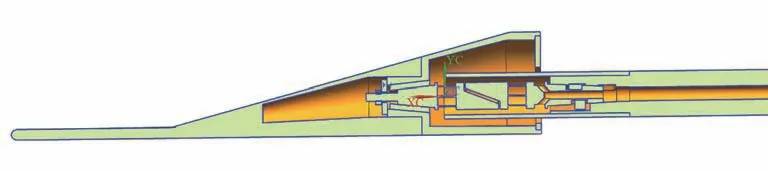
图6 三角翼试验方案图Fig.6 Schematic diagram of experimental delta wing
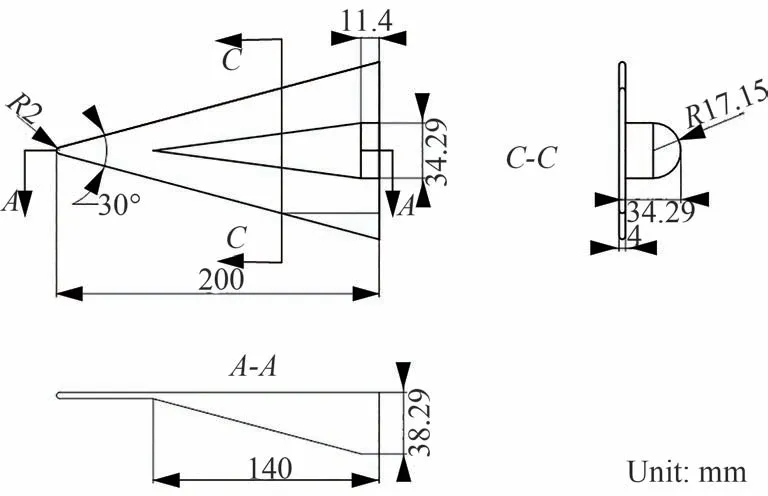
图7 三角翼尺寸示意图Fig.7 Sketch of delta wing dimension
复杂升力体的试验条件如表4 所示。升力体外形微量气动力测力试验采用FD-16 风洞所能达到的最稀薄状态,即总压最低、雷诺数最低、模拟高度最高,探索微量天平在跨流域极限状态下的测量能力。

表4 三角翼升力体外形试验条件Table 4 Test conditions of delta wing
三角翼升力体外形的试验结果如表5 所示。其中,参考长度0.2 m,参考面积0.001 468 m2,力矩参考点为升力体头部理论驻点,即坐标原点(0,0,0)。具体坐标系如图8 所示。
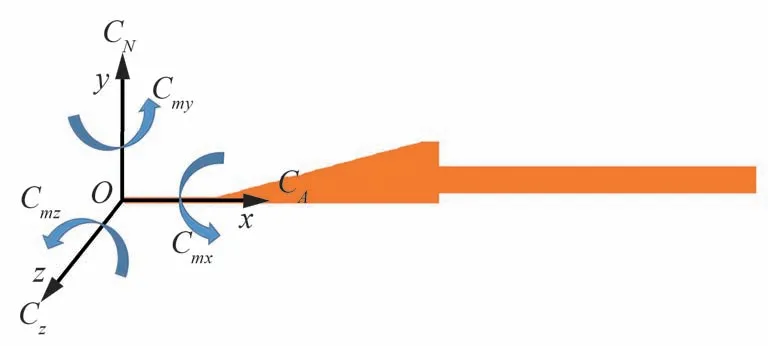
图8 升力体坐标系定义及气动力系数示意图Fig.8 Diagram of lift body coordinate system definition and aerodynamic coefficient diagram
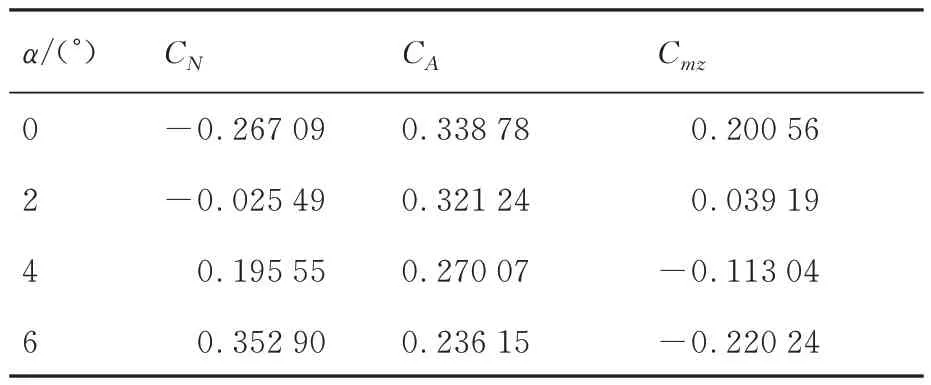
表5 三角翼升力体外形微量气动力试验结果Table 5 Experimental aerodynamics of delta wing lift body micro aerodynamics
从表5 中可以看出,在攻角为0°和2°时,法向力为y轴负向,攻角大于2°时,法向力为y轴正向;轴向力随着攻角的增大而减小;俯仰力矩由低头转为抬头,其绝对值先减小后增大。
2 数值计算方法
为与前文中微量天平的测力试验结果互相对比验证,本文采用数值模拟手段对跨流域微量气动力进行分析。
2.1 控制方程
控制方程是三维完全Navier-Stokes方程[22],为
式中:Q为守恒变量张量;F为对流通量张量;G为黏性通量张量。在笛卡尔坐标系下,其具体表达式为
式中:ρ为密度;u、v、w分别为x、y、z这3个向上的速度分量;p为压力;T为温度为单位质量的总能量,e为单位质量的内能;h=为单位质量的焓;k为热传导系数。
2.2 数值方法
本文使用AUSM+up(Advection Upstream Splitting Method +up)格 式[23]进 行 数 值 求 解。AUSM 类格式的主要思想认为流场在传播中存在对流与声波影响,分别考虑2 个过程,将无黏项分为对流项和压力项,基于马赫数对两者分别进行特征分裂,是一类高精度格式[24]。
2.3 时间格式
时间格式采用无条件收敛的LU-SGS 格式,本节仅给出针对无黏项进行隐式处理的时间格式表达。对于有限体积半离散格式,无黏通量采用隐式格式[24]处理,黏性通量采用显式处理。
2.4 滑移边界条件
在滑移流计算中,采用经典Maxwell 滑移边界条件,其速度滑移和温度跳跃为
式中:n代表垂直壁面的方向;x代表与壁面相切的方向;μ为气体黏性系数;γ为气体比热比;Pr为普朗特数;常系数A、动量调节系数σ和能量适应系数α'由壁面的物理特性及气体属性决定;λ为分子平均自由程。
3 计算结果及试验对比
3.1 简单钝锥外形
圆锥外形的为结构网格,采用商业软件生成。考虑到对称性,采用半模进行研究,流向× 周向×法向网格:171×41×101,且壁面第1 层网格距离1 × 10-6m,如图9 所示。

图9 钝锥计算网格剖面示意图Fig.9 Schematic diagram of blunt cone grid
在试验条件工况1 中不同攻角的圆锥表面压力等值线图如图10 所示,钝锥头部顶点压力最高,物面压力沿流向逐渐降低;随着攻角由-4°变为4°,圆锥的迎风面由y轴正向转到y轴负向。
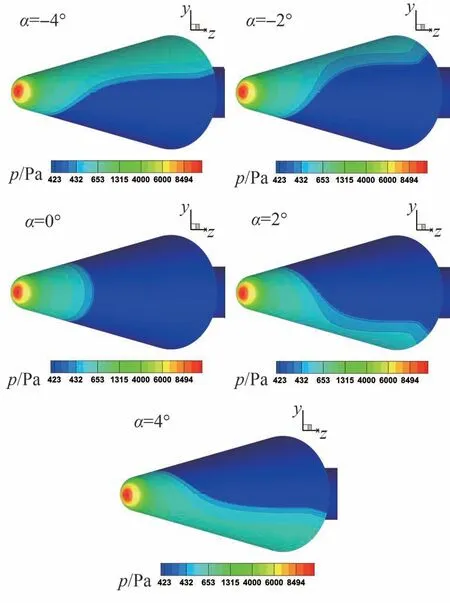
图10 不同攻角时圆锥表面压力等值线图(工况1)Fig.10 Pressure contour of blunt cone surface at different angles of attack (Case 1)
工况1 中不同攻角的对称面压力等值线图如图11 所示,超声速气流在钝锥头部形成弓形激波,导致钝锥头驻点部位压力升高;-4°攻角时,钝锥y轴正向为迎风面,超声速气流在钝锥迎风面受到压缩,形成压缩斜激波,导致钝锥y轴正向迎风面压力升高,钝锥背风面气流膨胀,压力降低;4°攻角的情况恰好与-4°相反。由图11 还可以看出,在0°攻角时,圆锥底部存在上下两个对称的分离涡,随着攻角绝对值的增大,其迎风侧的气流与钝锥身部物面的相对夹角增大,钝锥迎风面气流受到的压缩更强,而背风面气流膨胀更明显,从而导致钝锥迎风面压力升高,背风面压力降低;攻角绝对值增大时,更多的超声速气流向钝锥底部流动,冲击支撑,导致其迎风一侧的分离涡逐渐减小,背风一侧的分离涡逐渐增大。
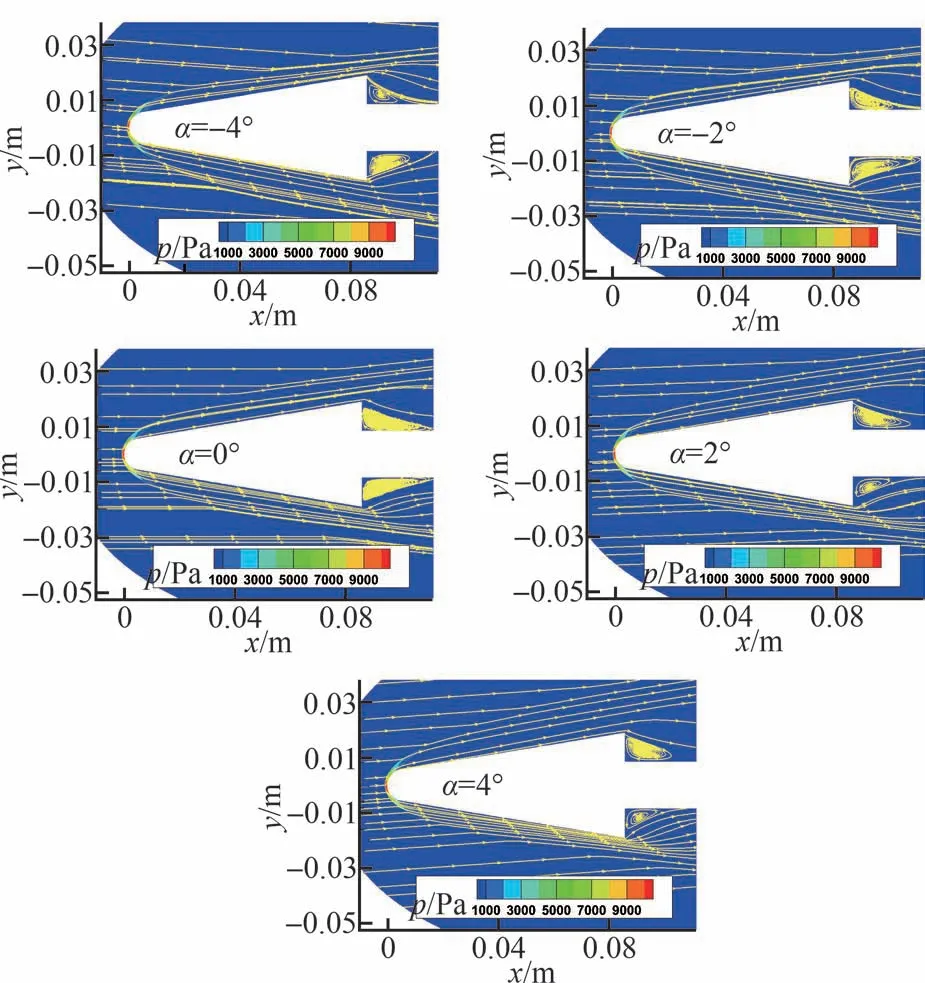
图11 不同攻角时圆锥对称面压力等值线图和流线示意图(工况1)Fig.11 Pressure contour and streamline on symmetry section of blunt cone at different angles of attack (Case 1)
工况1 中不同攻角的钝锥物面中心线压力变化趋势如图12 所示,在钝锥身部,随着攻角的增大,中心线迎风面压力逐渐增大,背风面压力逐渐下降,导致钝锥升力逐渐增大;圆锥底面压力较低;在支撑面上,压力也随着攻角的增大而升高。
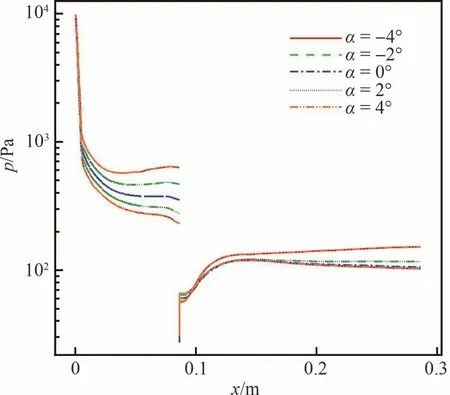
图12 不同攻角时圆锥物面中心线压力分布(工况1)Fig.12 Pressure distribution on wall center line of blunt cone at different angles of attack (Case 1)
工况1 中不同攻角的圆锥表面摩擦力x方向分量Cfx的等值线图如图13 所示,上述攻角范围内钝锥肩部的摩阻最大,而头部的摩阻很小。
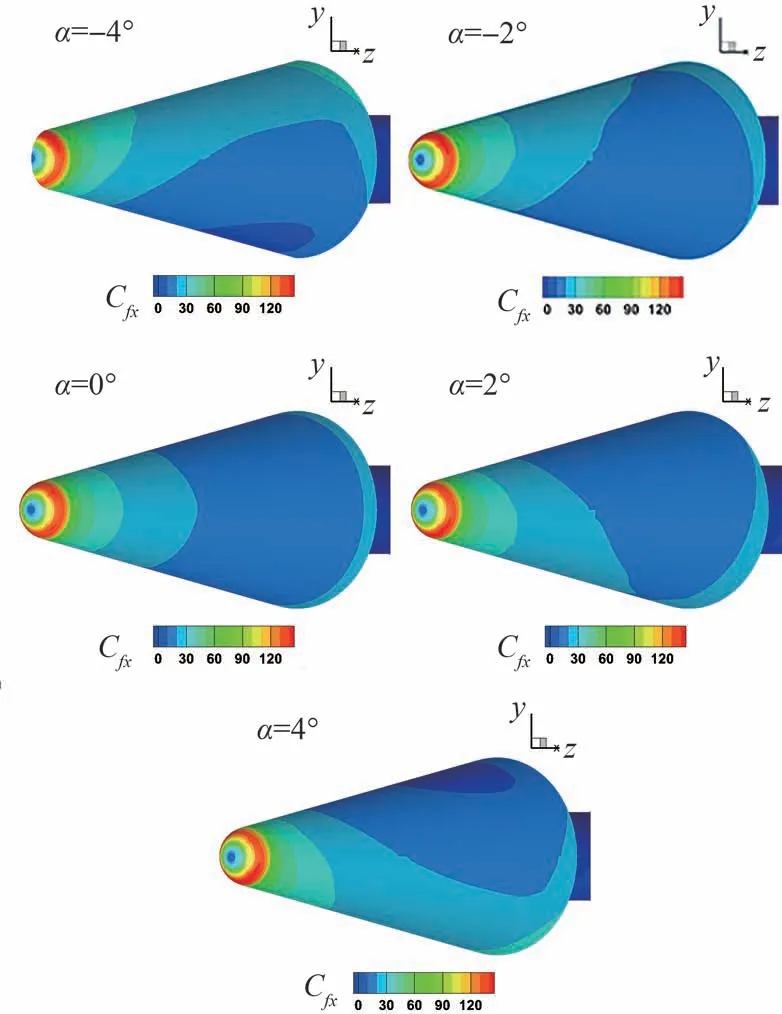
图13 不同攻角时圆锥表面摩擦阻力等值线图和流线示意图(工况1)Fig.13 Skin friction contour and streamline of blunt cone surface at different angles of attack (Case 1)
钝锥外形为工况1 时压力产生的轴向力系数(Pcx)和法向力系数(Pcy)以及摩阻产生的轴向力系数(fcx)和法向力系数(fcy)如表6 所示,在跨流域阶段,钝锥外形的压阻占主要地位,对轴向力系数而言,压力产生的轴向力约为摩阻的6倍,而法向力则高达26倍,且该比值几乎不随着攻角而变化。

表6 钝锥表面压力和摩阻系数 CFD 计算结果(工况1)Table 6 Pressure and skin friction CFD results of blunt cone (Case 1)
钝锥外形气动特性计算与试验结果的对比如图14 所示,跨流域微量气动力中的CN和Cmz计算结果与试验结果符合良好,说明本文设计的微量天平可以用于跨流域条件下的CN和Cmz气动力测量;对于CA,CFD 计算结果与风洞试验结果相差较大,分析其原因可能是在钝锥试验中,试验本身存在一定的偏差,如表3 所示,试验模型较小、气动力较小微量天平气动力测量也存在误差,可能是试验件支撑结构引起的误差,导致CFD 轴向力CA结果与试验结果相差较大。

图14 不同攻角时圆锥微量气动力CFD 计算结果与风洞试验结果对比Fig.14 Cone micro aerodynamics comparison between CFD result and wind tunnel test at different angles of attack
3.2 复杂升力体外形
三角翼升力体的计算网格同样采用商业软件生成,半模的流向×周向×法向网格为:181×91×141,且壁面第1 层网格距离为1×10-6m,如图15 所示。

图15 三角翼升力体计算网格剖面示意图Fig.15 Schematic diagram of delta wing computation grid
不同攻角时三角翼升力体表面压力等值线图如图16 所示,三角翼升力体头部顶点压力最高,物面压力沿流向逐渐降低;随着攻角由0°变为6°,三角翼升力体的迎风面由y轴正向转到y轴负向,且迎风面压力随着攻角绝对值的增大而逐渐增大,从而导致三角翼升力体压阻的法向力增大,轴向力增大。
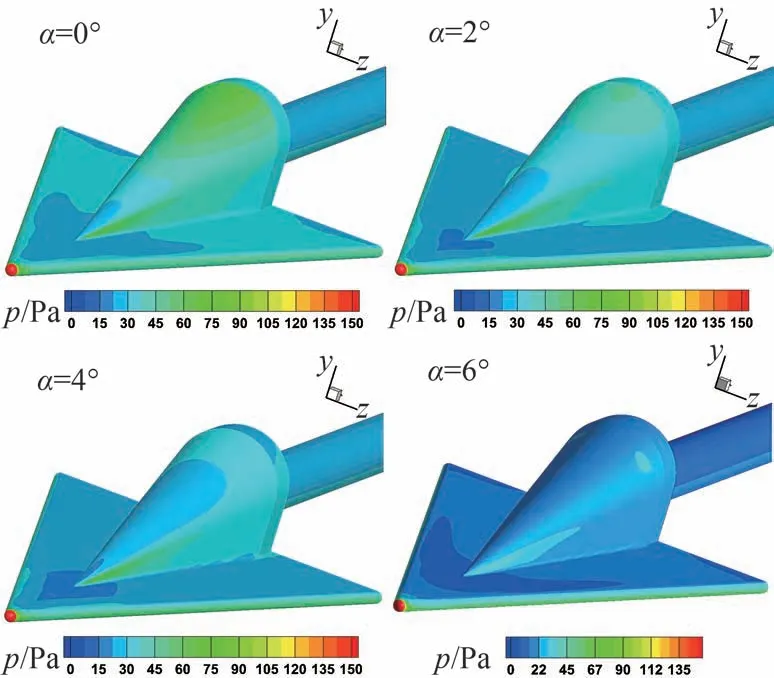
图16 不同攻角时三角翼升力体表面压力等值线图Fig.16 Pressure contour of delta wing surface at different angles of attack
不同攻角的三角翼物面中心线压力变化趋势如图17 所示,在三角翼身部x= 0.07 m 之前,迎风侧压力随攻角增大而升高,背风侧压力则降低,在x= 0.07 m 之后底部之前,表面压力随攻角的变化趋势发生变化,在0°攻角时,其物面中心线上下压力差最大,故而升力也最大。
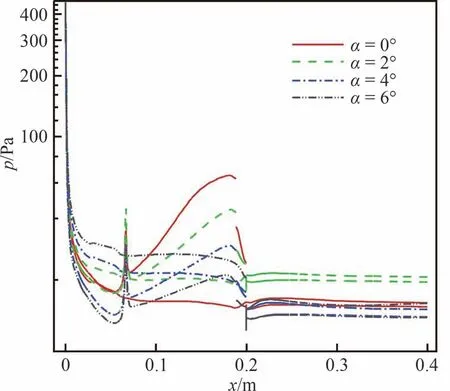
图17 不同攻角时三角翼升力体物面中心线压力分布Fig.17 Pressure distribution on wall center line of delta wing at different angles of attack
三角翼升力体压力产生的轴向力和法向力系数及摩阻产生的轴向力和法向力系数如表7 所示,在跨流域阶段,对三角翼升力体外形而言,由于试验环境更加稀薄,摩阻和压阻的比例相当。
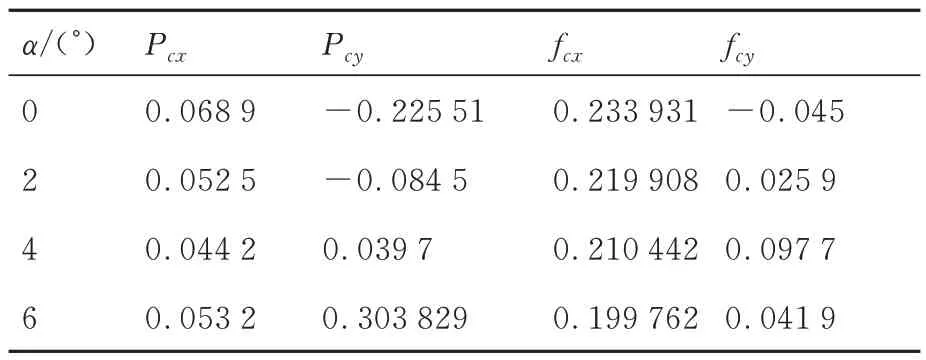
表7 三角翼升力体表面压力和摩阻系数CFD 计算结果Table 7 Pressure and skin friction CFD results of delta wing
三角翼升力体气动特性计算结果与试验结果的对比如图18 所示,可以看出对于升力体试验模型,跨流域微量气动力试验结果与CFD 计算结果符合程度要比简单钝锥模型差一些。分析其原因,作者认为在该稀薄试验条件下,流动虽然属于跨流域阶段,但是更靠近过渡流区的下边界,除了升力体试验本身带来的误差外,本文考虑滑移边界条件的求解N-S 方程的CFD 计算方法也是导致该误差的原因,因此,对于此类更为稀薄的试验条件,在以后的研究中应该寻找更适合稀薄流域计算的直接模拟蒙特卡洛(Direct Simulation Monte Carlo, DSMC)方法。
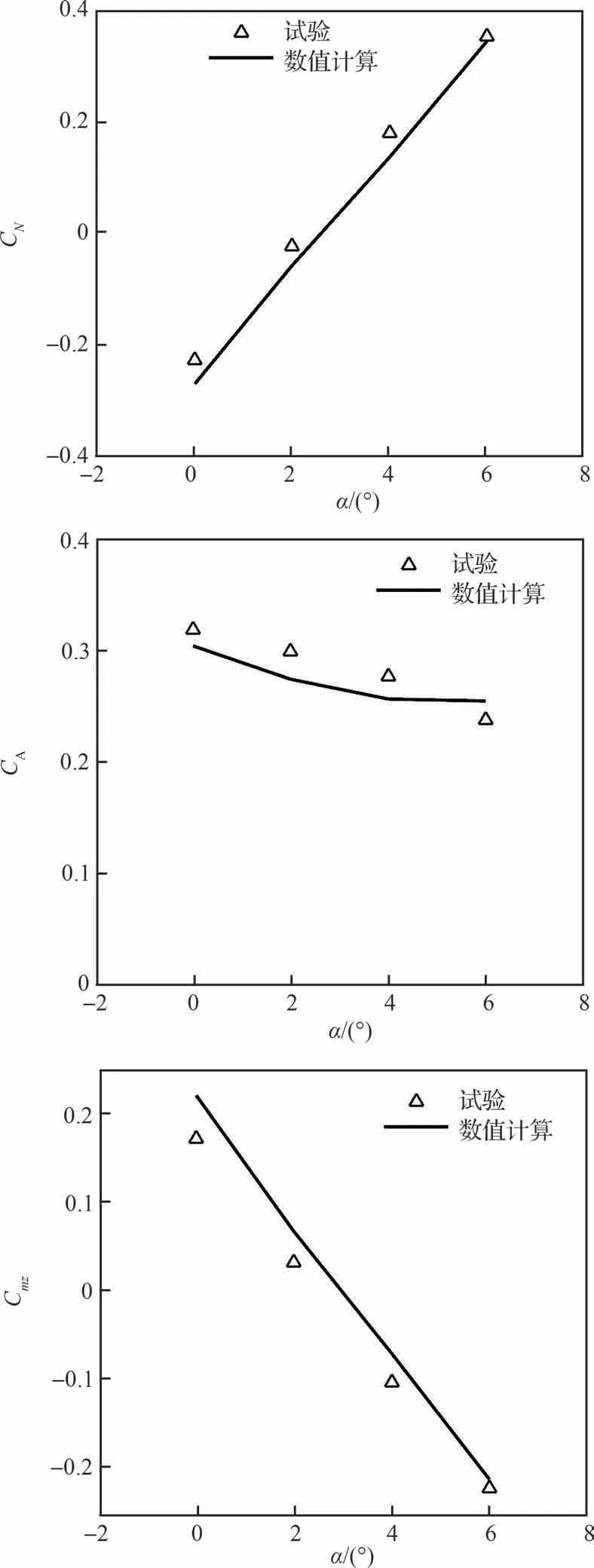
图18 不同攻角时三角翼升力体微量气动力CFD 计算结果与试验结果对比Fig.18 Micro aerodynamics of delta wing comparison between CFD results and test results at different angles of attack
4 结 论
针对跨流域环境的气动力风洞试验测量需求,研制了微量天平测力系统,采用钝锥简单外形进行了验证试验,并对三角翼升力体复杂外形进行了探索试验,通过数值计算方法对试验结果进行了验证,得到以下结论:
1)钝锥外形验证试验中,3 次试验时天平各载荷单元的气动数据重复性精度均优于4.8%,说明未来天平测量数据的重复性较好。
2)探索试验中,三角翼升力体外形采用了该风洞目前能达到的最低状态,试验结果表明该微量测力天平在极限状态下表现较好。
3)数值计算得到的钝锥和升力体气动力与微量天平测力吻合结果较好,校验了微量天平测力系统的可靠性,并实现了试验测量和数值模拟的相互验证。
4)对于简单钝锥外形,在其试验条件下,钝锥表面压阻远高于摩阻。
5)对于复杂三角翼升力体外形,其试验条件更加稀薄,三角翼表面摩阻占比与压阻相当。

