贝叶斯推理运动轨迹相干累积的动目标检测方法
杨文彬,王悦斌,李旦,,张建秋
1.电磁波信息科学教育部重点实验室,上海 200433
2.复旦大学 信息科学与工程学院 电子工程系,上海 200433
为了提高雷达对弱目标的探测能力,对多脉冲回波信号进行长时间相干积累(Coherent Integration, CI),理论和实践都证明是一种行之有效方法[1]。动目标检测(Moving Target Detection, MTD)[1]是长时间相干累积中最常用的方法。该方法通过慢时间维的快速傅里叶变换,可实现回波能量在多普勒域的聚焦,提高了探测信噪比(Signal-to-Noise Ratio, SNR)[2-3]。 然 而,在MTD 的应用中,对具有未知运动形式的机动目标,进行长时间的积累将面临两大问题:一是目标的高速运动,将可能导致相干处理间隔(Coherent Processing Interval, CPI)内的回波包络跨越距离单元(Across Range Unit, ARU),产生距离徒动(Range Migration, RM)[3];二是目标的加速运动,将可能导致跨多普勒分辨单元的多普勒频率徒动(Doppler Frequency Migration,DFM)[4]。这2 个问题会极大地降低脉冲多普勒雷达的相干积累增益[5]。
针对由目标高速运动导致的线性距离徒动,最常见的2 种处理方法是Keystone 变换[3]和Radon 傅 里 叶 变 换(Radon Fourier Transformation, RFT)[6]。Keystone 变换通过插值的方式,解耦快和慢时间维频率的耦合关系,以补偿目标回波中的距离徒动。而RFT 则通过距离-速度的联合搜索来克服距离徒动。但是,它们均忽视了非合作目标可能的加速运动,因此不能同时对距离和多普勒徒动进行补偿[7]。
为补偿由目标高阶运动导致的距离和多普勒徒动,近年来文献报道了一系列改进算法。这些方法大多假设目标的运动可由不大于三阶的多 项 式 描 述[4]。 其 中,高 阶Keystone(High-Order Keystone)变换[8]能实现快和慢时间维度高阶运动项间的解耦,但在校准多普勒徒动时会引入新的距离徒动,增加了后续处理的复杂性。为了不引入新的距离徒动,文献[9]提出了广义的RFT(Generalized Radon FFT, GRFT)。理论上,当目标的运动能用三阶多项式准确描述时,GRFT 通过对目标四维运动参数空间(距离、速度、加速度和加加速度)的联合搜索,可准确地估计出目标的运动轨迹,并实现高能量集中度的相干累积。但这样复杂的搜索过程,在实际中几乎不可能实现[5]。为了降低复杂度,文献[7]报道了一种Radon 变换及改进高阶全称吕分布(Radon-Modified High-order LV’s distribution, R-MHLV)的算法。该算法首先在距离-速度域内,利用Radon 变换进行二维搜索,粗略提取目标的运动轨迹。基于提取的轨迹,改进高阶吕分布(Modified High-order LV’s distribution,MHLV)就可用于估计目标的多项式运动参数。利用运动参数补偿距离/多普勒徒动后,就可实现目标的探测以及距离/速度的估计。然而,MHLV 是一种四阶非线性变换,其交叉项在低信噪比时将难以抑制[10]。为了克服非线性带来的影响,文献[10]报道了一种Radon 变换及二阶补偿(Radon Second-order Compensation,R-SC)算法。该算法首先对距离徒动进行粗估计,然后通过速度-加速度联合的二维搜索来构造匹配滤波器(Matched Filter, MF),以实现距离和多普勒徒动的补偿。该方法是一种线性方法,在低信噪比表现尚可。但是,同R-MHLV 一样,它依然需要进行多维参数联合搜索。
针对上述算法复杂度较大的问题,近年来文献报道了一些非搜索类的算法,如相邻交叉相关函 数(Adjacent Cross Correlated Function,ACCF)[5]、距离频率多相变换(Range Frequency Ploy Phase Transformation, RFPPT)[11]、时间翻转-非参数重采样稀疏长时间相干累计(Time-Reversed and Non-Uniform resampling Sparse long-time Coherent Integration,TRNU-SCI)[12]等。这些算法一般依赖精心设计的某种自相关函数,并结合LV 分布等信号参数估计算法,来获得描述目标多项式运动模型中的参数。然而,高阶自相关函数和LV 分布的非线性,将使得目标回波信号间,以及目标回波与噪声间产生难以抑制的交叉项。这些交叉项,甚至有可能淹没原有的目标信号,如此就增加了算法对检测条件的要求[7,13],进而极大地限制了它们的应用。
针对脉冲回波处理间隔内,待检测目标存在未知的距离和/或多普勒徒动问题,本文提出了一种贝叶斯推理运动轨迹相干累积的动目标检测方法。首先,通过对脉冲压缩回波信号的距离频率进行翻转,就可从未翻转与翻转后回波信号相乘的傅里叶逆变换中,提取慢时间维描述多目标运动的时频信号。当视该时频信号中各目标运动为状态变量,慢时间维时频信号为它们的观测时,就为多目标运动轨迹的估计,建立起了可据贝叶斯滤波推理的状态空间模型。一旦推理获得了各目标运动轨迹,就可构建出快和慢时间维联合的匹配滤波器来补偿因目标运动可能产生未知的距离和/或多普勒徒动,进而为高/超机动目标的探测提供了新方法。由于本文算法无需进行三维及以上搜索,因此就可在较低的计算复杂度下,实现多机动目标的检测。理论分析和仿真实验均证明,本文提出的算法适用具有复杂且未知运动状态的目标,且呈现出了优于文献报道方法的性能。
本文结构安排如下:第1 节介绍了脉冲多普勒雷达系统的信号模型;第2 节提出了贝叶斯推理目标运动轨迹的方法;第3 节给出了相干累积方法及算法流程;第4节分析了输出信噪比和计算复杂度;第5节给出了数值仿真实验结果;第6节总结全文。
1 信号模型
一脉冲多普勒雷达在M 个脉冲构成的一个CPI 内,发射信号可表示为[1]
式中:τ 表示快时间;ϕ(τ)为脉冲信号,其持续时间为Tp;tm=(m-1)Tr(m=1,2,…,M )表示慢时间;Tr≫Tp为脉冲重复间隔(Pulse Repetition Interval,PRI);f0表示雷达的工作频率。不失一般性地假设脉冲信号为线性调频(Linear Frequency Modulation, LFM)信号[1]:
在单次脉冲压缩(Pulse Compression,PC)的过程中,可假设目标不发生移动[1]。那么,当发射的脉冲由空间中K 个点状目标反射并接收,再经解调得到的二维基带回波信号就可建模为[1-2]
式中:Areck和Rk(tm)分别为第k 个目标反射信号的幅度和在慢时间维度上描述其运动的函数;c 为光速。一般地,Rk(tm)可表述为[10]
式中:Rk,0为目标的初始位置;ΔRk(tm) 是运动轨迹,为连续函数,如:三阶多项式ΔRk(tm)= vktm+αkt2m+βkt3m,其中:vk、αk、βk分别表示目标的速度、常加速度和加加速度[5]。
经过脉冲压缩后,二维接收回波信号式(4)可进一步表示为[1]
式中:Ak表示脉冲压缩后第k 个目标的幅度。由式(5)可知,运动轨迹大于距离分辨率时,将导致距离徒动;与此同时,当ΔRk(tm) 呈非线性变化时,将可能导致多普勒徒动。为了提高雷达长时间相干积累的增益,就需要对距离和多普勒徒动进行补偿,否则将以高概率发生漏警[4-5]。
2 动目标运动的估计
为补偿距离和多普勒徒动,就需要获知目标的运动轨迹。为了估计它们,本节将研究慢时间维时频信号的提取,以及基于提取的时频信号,估计运动轨迹的方法。
2.1 多目标慢时间维信号提取
为提取出式(5)中与多目标运动相关的信号exp[-j4πf0Rk(tm)/c] ,k=1,2,…,K,对回波信号进行快时间维傅里叶变换(Fourier Transform,FT),即将信号s(τ,tm)变换到距离频率-慢时间(Range-Frequency Versus Slow-Time)域上有
式中:f ∈[-fs/2,-fs(N-1)/2N,…,fs2 ]为距离频率单元;fs为采样频率;N 表示快时间维上的采样数目;AFk表示第k 个目标频域上的幅度。
对式(6)中的二维信号,以0 频率为中心,对其进行上下翻转后得:
式中:sself(τ,tm)和scross(τ,tm)分别表示信号的自项和交叉项,表达式分别为
式中:ak表示第k 个目标自项的幅度;bk,ρ表示第k和第ρ 个目标间交叉项的幅度。式(8)和式(9)的推导请参见附录A。
信号s2(τ,tm)中有且仅有sself(τ,tm)集中在τ=0附近,就有:
2.2 目标运动轨迹估计
式(10)给出的信号,可由文献中报道的任一时频分析方法,获取目标运动轨迹的时频图。可是,如何将时频图与目标关联却是一件困难的工作[14]。为解决这一问题,本节将介绍运动轨迹估计的方法。为了描述的简洁,首先引入一变量
文献[15]报道了一种利用多项式预测模型(Polynomial Prediction Model,PPM),对式(11)相位进行建模的方法。在其模型中:
式中: xk(tm)=[k(tm),θk(tm),…,θk(tm)]T∈R(L+1)×1表示联合状态矢量;F ∈R(L+1)×(L+1)表示如下状态转移矩阵[14]:
ζk(tm)∈R(L+1)×1是描述使用分段低阶多项式近似式(10)中模型时的误差。该误差可表示为0 均值的高斯噪声,且噪声的协方差矩阵为对角矩阵对角线上的元素σl,l=1,2,…,L 则是信号相位的扰动强度。
综上,式(10)可由如下的状态空间模型描述[14,17]:
式中:η(tm)为均值为0 的测量噪声,其方差的估计2η将 在2.3 节 中 给 出。如 此,当 目 标 数 目K 已知时,非线性贝叶斯推理的滤波算法,如扩展卡尔曼滤波(Extended Kalman Filter, EKF)、无迹卡 尔 曼 滤 波(Unscented Kalman Filter,UKF)[17],就可对状态空间模型进行推理了。
2.3 滤波算法初始化
在应用中,雷达观测的目标数一般是未知的,因此为估计式(10)中信号的目标数K,本节将给出基于稀疏迭代自适应协方差估计(SParse Iterative Covariance-based Estimation, SPICE)的方法。SPICE 将求解如下加权协方差拟合(Weighted Covariance Fitting, WCF)问题[18]:
式 中:y0=[ y(t1),y(t2),…,y(tD)]T∈CD×1表示慢时间维信号最初D≪M 个观测数据,通常可以认为其是近似平稳的,这意味着y0可用线谱模型来 描 述[14];||·||F表示 矩 阵 的Frobenius 范 数。观测数据的协方差矩阵R 建模为[18]
式 中:q ≜[q1,q2,…,qI+N]T∈R+I+N为 上 述 协 方差的模型参数。令I 表示离散化的频点个数,B=[b(ω1),b(ω2),…,b(ωI)]∈CD×I表示 频 率 的 导向 矩 阵 , 其 每 一 列 b(ωi)=是离散频率ωi的导向矢量。
式(17)中的加权协方差拟合问题,可由如下迭代的方式求解[18]:
式中:i = 1, 2,…, I + D;当i ≤ I 时,βi= D2,当i > I 时,βi= 1;R̂j-1表示 第j-1 次 迭 代 过 程中的协方差估计值。当算法收敛或达到预设迭代次数时,就可由式(18)获得拟合的协方差。基于该协方差,使用判别函数估计法(Discriminant Functions Estimator, DFE)等 就 可 获 取式(10)中观测目标数的估计K[19]。
从式(18)可知,当协方差估计完成后,qs=[q1,q2,...,qI]T就是信号的功率谱。这也就意味着:K 个目标就对应于qs中K 个最大的局部峰值。令k和k,0分 别 表示 第k 个 目 标 幅 度 和 频 率的估计,那么第k 个目标初始幅度和相位因子的估计就为
考虑到式(14)状态矢量xk(t1)中的各相位存在如下关系[14]:
取θk(t1)=0 时,xk(t1)中各相位的初值便可由式(22)递推关系得到。
由式(18)也可知,SPICE 同时对观测噪声进行了建模,这样观测信号的噪声协方差就可估计为
值得注意的是,基于式(20)和式(21)的初始化方式可能存在误差,但这些误差都可以用式(16)状态空间模型中的过程噪声描述,且随着滤波算法的进行,初始化的估计误差带来的影响将会逐步减小[17]。除此之外,DFE 在低信噪比下更倾向于多估计目标[19],但对于动目标检测而言,即使出现少量的“虚假目标”,在3.1 节中也会因为在相干累计时能量集中度低而被消除。
3 相干累积
3.1 匹配滤波相干累积
目标的高速运动常导致速度模糊现象[20]。这样第k 个目标的运动轨迹的估计ΔR̂k(tm)和推理得到的(tm)间将存在如下关系[20]:
式中:pk∈Z 表示模糊整数(Ambiguous Integer)[20]。一般地,模糊整数是未知的,这样就无法由式(24)正确地估计目标的位移。为此,本节将使用一种搜索的方式对目标进行相干累计。
对第k 个目标,p ∈Z 对应的轨迹估计为
其中:
令δRk(tm,p)=ΔRk(tm)-ΔR̂k(tm,p)表示距离徒动的补偿残差,则从式(27)可以看到:当δRk(tm,p)=0 时,有:
此时式(29)中第k个目标因其运动而产生的距离和多普勒徒动可完全消除。不过S͂pother(f,tm)依旧会对第k个目标的检测产生干扰。为抑制这种干扰,可先将式(27)变换到快时间域,随后进行慢时间维傅里叶变换得:
式中:AOk代表第k个目标的输出幅度 ,fd∈[-0.5,-(M-2)/2M,…,0.5]则表示归一化的多普勒频率。显然,式(30)中有且仅有第k个目标的信号集中在fd=0 附近,而其他目标的影响将得到抑制。定义输出的距离聚焦分布为
若p取不同值时,在一个CPI 内造成的位移大于一个距离分辨单元,则仅存在一个p使得|Ck(τ,p)|2最大。这样,目标初始位置和模糊常数的联合估计为[3]
对应地,瞬时速度的估计为[3]
式 中:vb=c/2f0Tr表示 盲 速 度(Blind Speed);vambk∈[-vb/2,vb/2]为模糊速度(Ambiguous Velocity)。一般而言,模糊整数的搜索范围有限[3,20],故上述流程能以合理的计算复杂度校准距离徒动。
3.2 算法流程
图1 给出了本文提出的贝叶斯推理目标运动轨迹相干累积的机动目标检测算法流程图。
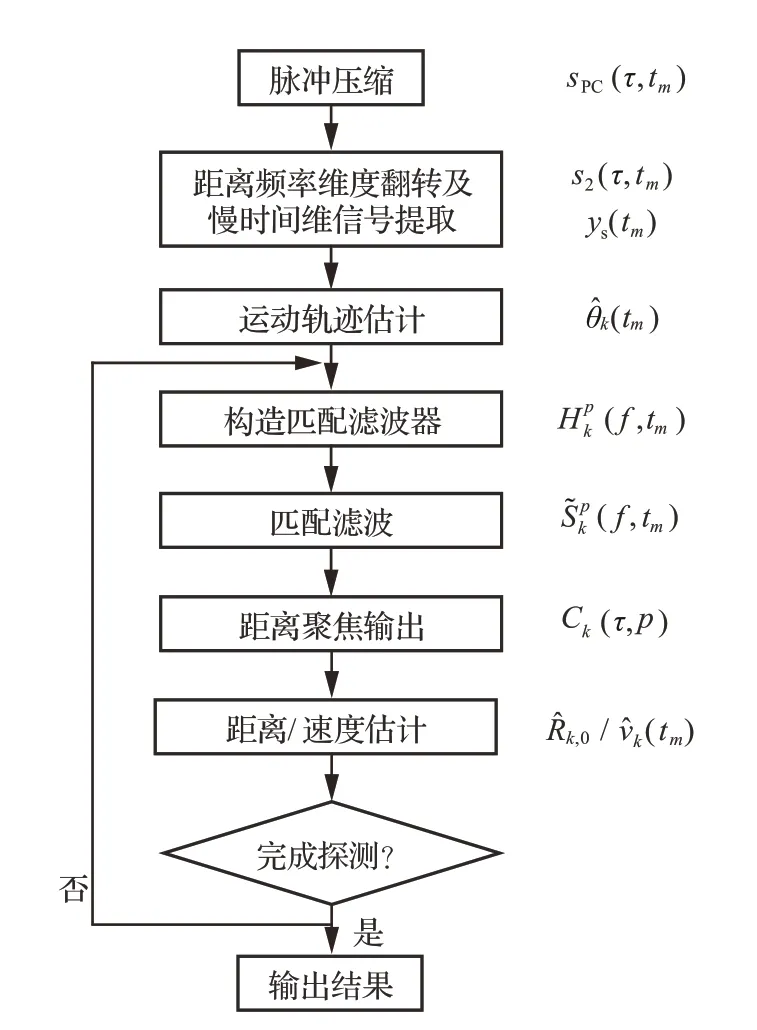
图1 本文提出算法流程图Fig.1 Flow chart of the proposed algorithm
4 性能分析
4.1 输出信噪比
考虑仅含单一机动目标回波的信号:
式中:ε(τ,tm)表示脉冲压缩后的加性高斯白噪声。
不失一般性地,假设目标的模糊常数p1已知,这样使用匹配滤波器H1p1(f,tm)对噪声进行处理后将得到
式(35)中的噪声将服从复高斯分布CN (0,Mσε2)[20]。定 义 输 入 信 噪 比 为SNR1IN=A21/σε2,则 由 柯 西- 施 瓦 茨 不 等 式(Cauchy-Schwarz Inequality)知,当θk(tm)的估计存在误差,即H1p1(f,tm)非完美时,输出信噪比将有如下关系:
式 中:ξ(tm)=θ(tm)-(tm)=cδR1(tm)/4πf0表示非理想匹配滤波时的估计误差;0 <ψ<1 表示增益损耗率。由式(36)则可知,CPI 内脉冲数越多,匹配滤波器越完善,输出信噪比将越高。输出信噪比的分析详见附录B。
4.2 算法复杂度
本文算法主要存在如下运算量:
1) 慢时间维度信号提取阶段:需进行M次快时间维度IFFT,复杂度Ο(MNlog2N)。
2) 轨迹推理阶段:初始化时,SPICE 运算复杂度主要在矩阵求逆上[18],其复杂度近似为Ο(I3)。而滤波时运算量主要来自于矩阵求逆,故滤波的复杂度为Ο(M((L+1)K)3)[21]。
3) 相干累积阶段:设模糊常数的搜索数为Np,则每个目标每次需进行M次快时间维IFFT和N次慢时间维的FFT,以及MN的乘法,总复杂度为
若有K≪M<N[20],则本文中的算法复杂度可近似表示为
表1 中总结了在机动目标满足三阶多项式运动假设时,MTD、RFT[6]、R-SC[10]、R-MHLV[7]、TRNU-SCI[12]以及GRFT[9]这6 种对比算法的算法复杂度。表1 中,Nv、Nα和Nβ分别为三阶多项式模型的无模糊速度、常加速度、加加速度的搜索格点数。由表1 可以发现:基于多维参数搜索的算法,其复杂度将远高于本文算法;但本文算法的复杂度略高于TRNU-SCI。图2 中展示了各算法在目标数K=2 时,不同脉冲数下运算复杂 度 对 比,其 中,I=Nv=Nα=Nβ=M;N=1 024。

表1 算法复杂度比较Table 1 Comparison of computational complexity

图2 计算复杂度曲线Fig.2 Curves of computational complexity ratio
5 数值仿真
为评价本文提出算法的性能,本节将给出数值仿真结果。仿真系统的参数如表2 所示。若不特别说明,本文仿真中的参数均遵循表2 中的设置。设雷达需探测的速度范围为[-1 200 m/s, +1 200 m/s],则模糊常数搜索范围为[-10, 10]。
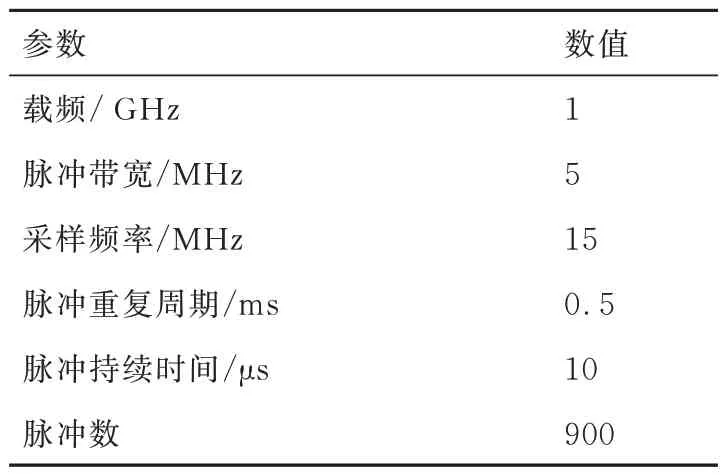
表2 雷达仿真参数Table 2 Simulation parameters of radar
5.1 算法有效性验证
本节将讨论存在多个机动目标时,相干累积探测目标的结果。如表3 所示,是符合三阶运动假设的目标1 和2 的参数。

表3 高速目标参数(目标1 和2)Table 3 Parameters of high-speed targets(Target 1 & 2)
实际目标一般都是运动模式未知的非合作目标。故在本小节中加入具有复杂的高阶运动模型的目标3。目标的初始位置为6.80 km,幅度同目标1,运动轨迹为
脉冲压缩后,回波信号的对目标1 的信噪比为6 dB[7]。综合考虑滤波算法复杂度与滤波的性能,选用UKF 作为式(16)的非线性滤波算法[14]。滤波算法的复杂度将随着L增加而增加[14,17],而二阶多项式模型足以描述复杂的机动特性,故本文中FIR的抽头数L= 3,且对应的多项式模型阶数为2。在滤波器的初始化阶段,取D= 48,SPICE 中的频点数取I= 512,迭代次数为6。实验中,假设目标具有相同的过程噪声协方差,且其对角线上的元素为[1×10-4, 1×10-9, 1×10-9, 1×10-9],而观测噪声的方差则由式(23)估计得到。
图3 给出了本文算法的结果。图3(a)为经过脉冲压缩后的原始回波,此时,多个目标间的轨迹出现了显著的交叉。图3(b)为慢时间维时频信号的STFT 时频谱,此时目标的强机动性使时频谱出现了许多不连续的瞬时速度脊线。这就使得基于时频分布进行轨迹关联的瞬时速度估计算法,如三阶最大似然法(Quasi-Maximum Likelihood,QML)[22],自 适 应 迪 利 克 雷 混 合 模 型Rao-Blackwellised 粒 子 滤 波 器(Adaptive Dirichlet Process Mixture model-based Rao-Blackwellised Particle Filter, ADPM-RBPF)[23]等都将失效。与此同时,由于轨迹交叉现象的存在,快时间频域翻转结果中目标位置相同的时刻交叉项的能量不能被完全消除,出现了一些能量较高的点。但是,这些点一般具有突发性和短时性,可以看作是冲击性的噪声/杂波,并在滤波算法中或后续相干累积中被消除。图3(c)为文献[23]中基于STFT 时频脊线提取法获得的瞬时速度估计结果;图3(d)为基于本文算法得到的瞬时速度估计结果。对比图3(c)和图3(d)可以看到:得益于式(16)状态空间模型,在速度跨越盲速度周期/变化轨迹交叉时,本文算法依旧能得到连续的瞬时速度估计,也就是说,估计的目标运动轨迹是连续的。图3(e)为MTD 得到的相干累积检测结果,此时目标能量聚集度很差。为了绘制本文算法获得的相干累积分布,本文定义如下多普勒维向量:

图3 多目标的处理结果Fig.3 Drocessing results of multiple targets
接下来继续研究在不同信噪比条件下,所提出的算法对速度估计的相对均方根误差(Relative Root Mean Square Error ,R-RMSE)和检测率间的关系。速度估计的R-RMSE 定义为
式中:NMC表示蒙特卡洛仿真实验的次数,在本节中 取NMC=500;vk=[vk(t1),vk(t2),…,vk(tM)]T表示 目 标 的 真 实 速 度 矢 量则表示第n次实验中估计的速度矢量;||·||2表示向量的2 范数。仿真实验中,使用单元平均恒虚警检测(Cell-Averaging Constant False Alarm Rate, CACFAR)[1,5]器 检 测 目 标,其 虚 警 率 设 置 为Pfa=10-4。实验中加入的噪声为高斯噪声,且脉冲压缩后信噪比的变化范围为-20~20 dB。为了在低信噪比下获得鲁棒的探测效果,本文采取多级处理的方法[24],首先使用MTD 的距离速度谱以较高的虚警率大致确定目标的范围,再进行频率翻转操作提取慢时间维时频信号。图4 为目标3的实验结果,可以看出,速度相对误差随输入信噪比的增加而逐渐减小。
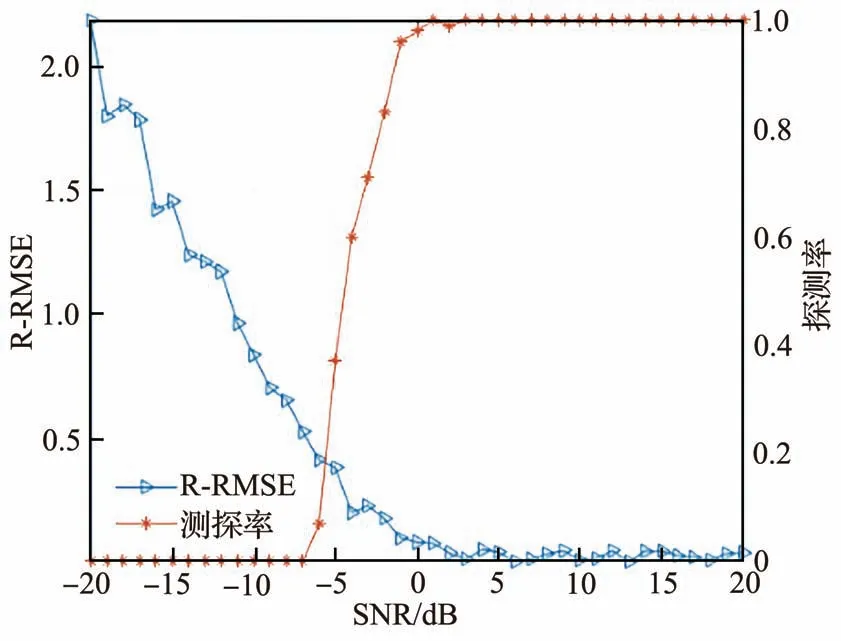
图4 目标3 不同信噪比条件下速度估计的R-RMSE 和探测率的关系Fig.4 Comparison of velocity estimation R-RMSE and detection probability of Target 3 with different SNRs
5.2 算法性能
5.2.1 相干处理结果
本 节 仿 真 实 验 将 给 出RFT[6]、R-SC[10]、RMHLV[7]以及TRNU-SCI[12]的检测结果,实验设置同5.1 节。
图5(a)~图5(d)分别给出了上述4 种对比算法的相干累积检测结果。图5(a)为RFT 方法的结果,几乎不能区分出任何一个机动目标。图5(b)为R-SC 的检测结果,可以看到,仅有目标2的相干累积能量集中度较高。图5(c)为R-MHLV 的检测结果,可以发现该算法对目标1 和2 具有较好的能量集中度。然而,对于具有复杂运动模式的目标3,基于目标三阶运动假设的R-MHLV,亦无法应对。图5(d)为TRNU-SCI 的输出结果,可以看到该算法的表现略差于R-MHLV,这是因为该算法的翻转操作在存在多个待测目标的情况下,会产生新的交叉项,在一定程度上会干扰二次运动项的检测,从而影响后续的距离/多普勒补偿。从图5 以及本文算法(图3(f))对目标3 的检测结果,可以看到本文算法优于对比算法;且目标1 和目标2 的相干累积效果,亦与R-MHLV 相当。
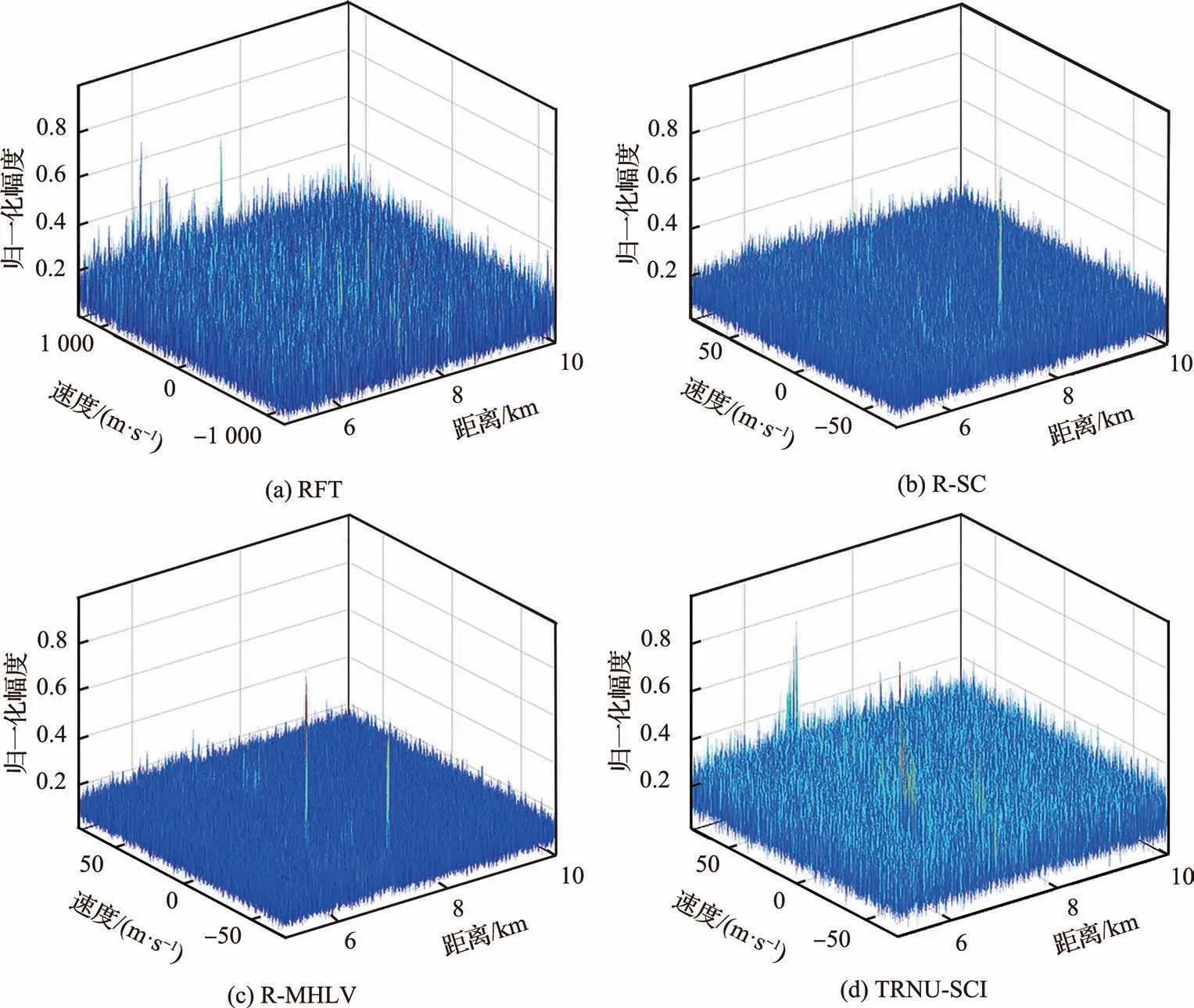
图5 4 种算法的相干处理结果Fig.5 Coherent integration results with four algorithms
5.2.2 目标探测性能
本节中将研究5.2.1 节中的各对比算法与本文提出方法在不同信噪比下对目标1和目标3的检测率。仿真实验中信噪比的变化范围从-30~20 dB,NMC=500,其余设置同实验5.1节。
图6 展示了各算法在不同信噪比下对目标1的探测率。可以看到:本文算法优于文献报道算法,但仍与GRFT 还有差距。这是因为目标1 满足三阶运动模型,而GRFT 通过对目标“距离-速度-加速度-加加速度”进行足够细致的多维联合搜索,可以达到理想的最大输出信噪比,从而获得最优的探测性能[11]。而本文所提出的算法,存在噪声时对轨迹的估计总会存在一定的误差,导致性能有所损失。
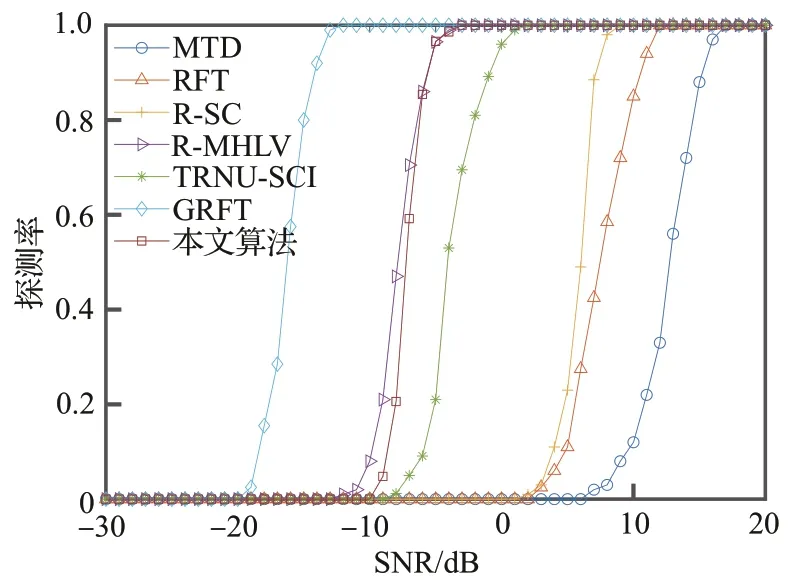
图6 各算法在不同信噪比下对目标1 的探测率Fig.6 Detection probability of each algorithms of Target 1 with different SNRs
图7 给出了各算法在不同信噪比下对目标3的探测率。可以看到,目标3 不满足三阶运动模型的目标,此时本文算法的探测性能优于GRFT。这说明,即使高超机动目标具有复杂运动模式,本文方法依旧能对其实现高能量集中度的相干累积。
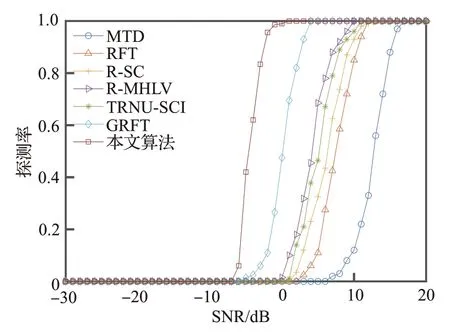
图7 各算法在不同信噪比下对目标3 的探测率Fig.7 Detection probability of each algorithms of Target 3 with different SNR
5.3 讨 论
估计信号分量数目时,窗长D是一个重要的参数。由谱估计理论可知:当观测长度为D时,其分辨率为1/D[25]。故在给出表2 基本参数条件下,能区分的2 个目标间的最小速度差为150/Dm/s。为了研究观测窗长D对目标数估计性能的影响,本节将研究不同窗长下,目标数估计的成功率与信噪比的关系。在本节实验中,所选用的目标回波信号中分别包含初始频率分别为1 000 m/s 和996 m/s 的2 个信号,除此 之外2 个信号的其余设定分别同5.1 节中的目标1 和目标2。为更好地展示窗长D对识别成功率的影响,本节实验仅在无噪情况下提取的慢时间维信号中添加高斯噪声,且信噪比的变化范围为[-15 dB,10 dB]。不同信噪比条件下,每组实验进行100 次蒙特卡洛仿真。
图8 给出了在不同信噪比和窗长D条件下,目标数识别的成功率。可以发现:D越大,在低信噪比下的成功率越高[25]。但这并不意味着D越大越好,因为D过大时观测窗内的数据将很难满足局部平稳条件,反而会使估计的成功率下降。

图8 不同信噪比下不同窗长的识别成功率Fig.8 Detection success rates for different window length at different SNR
6 结 论
针对雷达脉冲回波处理间隔内,由于未知的距离和/或多普勒徒动而导致待检测目标相干累积性能下降的问题,本文提出了一种贝叶斯推理目标运动轨迹相干累积的动目标检测方法。
1) 该算法使用距离频率翻转法获得慢时间维描述多目标运动轨迹的时频信号;随后,基于该信号构建多目标运动轨迹的状态空间模型就可实现目标运动轨迹的推理。
2) 基于贝叶斯滤波推理出的各目标运动轨迹设计出快-慢时间维匹配滤波器来补偿机动目标的距离和/或多普勒徒动,从而为高超机动目标的检测提供了手段。
3) 理论分析和仿真结果均表明本文提出的算法能适用于复杂的运动状态,在多机动目标的仿真检测中,呈现出了优于文献报道方法的性能。
附录A:
将S( f,tm)与S(tm)相 乘,可 得 距 离 频 率-慢时间维信号:
可以发现式(A1)中,当且仅当k=ρ 时,它的(a)项中指数为0 而且可完全消失。如此,式(A1)信号中仅留下与慢时间有关的部分。
对(A1)式中的进行快时间维的IFT,得
式中:sself(τ,tm)和scross(τ,tm)分别是式(9)的自项和交叉项。
附录B:
在匹配滤波器非理想的情况下,目标距离-多普勒位置处,相干累积的输出为
为了方便研究其性质,假设3.1 节中的估计结果,是对真实值的一种近似无偏估计,且其误差ξ(tm)服从均值为0, 方差为
的高斯分布[17]。那么可对式(B1)进行如下近似:
1) (a)项的sinc 函数可近似为[20]:
这样,(a)项的取值就可由一个伯努利分布(Bernoulli Distribution)近似描述为
在误差服从高斯分布的假设下,该伯努利分布 取1 的 概 率 为p1=p(|ξ(tm)|<π2f0/B),其 数值可由查表法获取。
2) (b)项可近似描述为[26]
其中:0 <γ <1 表示对相位估计的理想程度,或称为纯净度[26]。在上述噪声误差假设下,则有且
基于上述近似,易知(a)和(b)两项中的虽然有相同的变量,但由于二项分布的取值特性及正态分布的各向同性性,因此就可近似地认为(a)和(b)项中的随机变量相互独立。这样,式(B1)的期望就为
由柯西-施瓦茨不等式还可知,输出信噪的上界为
由式(B8),上述输出信噪比上界的期望为
据5.1 节给定的运动参数,本文下面将研究在不同CPI 长度的条件下,本文方法实际输出SNR,输出SNR 的上界与理想输出SNR 的关系。实验中CPI中脉冲数的范围从100~1 000,且每种CPI长度下进行500 次蒙特卡洛仿真。实验中,输出噪声协方差的估计方法与CA-CFAR 相同;理论上界中与目标运动相关相位的计算误差方差,则由式(B2)获得。从图B1 可以看出,所提算法的实际输出信噪比与理想情况相距不大。
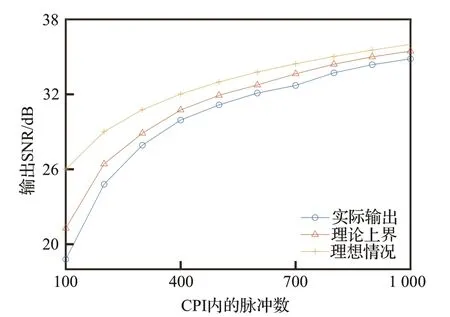
图B1 不同CPI 长度下本文算法实际输出SNR、理论输出SNR 上界与理想输出SNRFig.B1 SNR given by proposed algorithm, theoretical output SNR up-bound and ideal output SNR with different length of CPI

