预测-五阶容积卡尔曼滤波方法

赵祥丹，王彪，王志胜，杨忠

南京航空航天大学 自动化学院，南京 210016

自从卡尔曼将“状态空间法”引入到高斯滤波器中提出卡尔曼滤波器（KF）后，以递推形式呈现的高斯框架下的滤波方法相继而出。为适用于非线性系统，有学者提出扩展卡尔曼滤波器（EKF）将卡尔曼滤波器中线性系统条件转化为更一般的非线性系统，但EKF 只适用于弱非线性系统[1］。对于强非线性系统，常常采用确定性采样逼近高斯概率密度的Sigma 点卡尔曼滤波系列方法，其典型代表为无迹卡尔曼滤波（UKF）。2009 年，加 拿 大 学 者Arasaratnam 和Haykin 提 出了一种容积卡尔曼滤波器（CKF）[2］，该滤波方法以Sigma 点滤波为基础，采用球面-径向积分准则对高斯积分进行数值逼近并进行递推状态估计。相比于无迹卡尔曼滤波，容积卡尔曼滤波具有严格的数学推导，更加严谨且滤波精度更高。文献[3］在CKF 基础上，以任意阶全对称球面插值准则处理球面积分；以矩匹配法处理径向积分，提出了高阶容积卡尔曼滤波（HCKF）方法。文献[4］在文献[3］基础上，采用球面单形准则处理球面积分，提出了五阶容积卡尔曼滤波（5thCKF）方法。但上述方法均采用矩匹配法对径向积分进行数值计算，会导致径向积分的代数精度有所丢失。文献[5-8］对七阶容积卡尔曼滤波（7thCKF）进行了深入研究，其相较于五阶卡尔曼滤波精度有所提升，但所需采样点数过多，计算及其复杂，庞大的计算量使得算法很难应用于实际工程中。

高斯条件下的滤波器研究已经相对成熟，但实际系统仍然会存在有非高斯条件的情况，比如系统建模产生的模型误差等。文献[9］针对系统模型误差，提出一种预测滤波（PF）方法，该方法基于实际观测值和预测观测值求解模型误差得到新模型，进而求解状态方程组得到状态估计值，实际应用于非高斯过程噪声系统，但该方法求解状态方程组的过程过于复杂，在高维系统中难以实现。

为使滤波方法能够同时应用于强非线性系统和非高斯过程噪声系统，本文将高阶容积卡尔曼滤波和预测滤波方法相结合，提出一种预测-五阶容积卡尔曼滤波（P5thCKF）方法。采用球面单形准则处理球面积分，广义高斯-拉盖尔求积准则替代矩匹配法处理径向积分，以卡尔曼滤波递推求解替代预测滤波方程组求解，进一步提高滤波精度，且避免了精度损失和解方程组困难等问题。

1 高斯滤波框架

容积卡尔曼滤波是高斯滤波框架下的一种滤波方法，而高斯滤波又通过贝叶斯滤波发展而来。贝叶斯滤波的核心思想是通过先验信息和观测信息得到状态后验概率密度函数，进而通过后验概率分布求其期望、方差得到状态估计量。

假设系统方程为

式中：f (·)为状态转移函数；G 为过程噪声系数矩阵；h(·)为观测函数；x 为状态量；ω 为过程噪声；z为观测量；v 为观测噪声。由文献[10］可得贝叶斯滤波框架为

假设系统（1）各随机变量服从高斯分布，结合式（2）可得高斯滤波框架[10］。

1） 预测阶段

式中：xk|k-1、xk|k代表状态预测值和状态估计值；Pk|k-1、Pk|k代表状态预测方差阵和状态估计方差阵；zk|k代表预测观测值；zk代表实际观测值。从式（4）～式（9）可知，高斯滤波的关键问题是如何求解高斯积分：

相关证明可见文献[2］。

2 五阶容积卡尔曼滤波

容积卡尔曼滤波的核心思想是以高斯滤波框架为主体，对高斯积分（12）进行球坐标系变换得到球面-径向积分，进而用不同方法分别对球面积分和径向积分进行数值计算。为推导方便，式（12）简记为

对式（13）进行球坐标系变换得球面-径向积分，令x=ry （yTy=1，r ∈(0，∞)），式（13）等价为

式中：Un表示n 维超球体表面；dσ(y)表示面积微元，dr 表示半径微元。将式（14）拆分为球面积分和径向积分。

球面积分：

径向积分：

下文将分别对球面积分和径向积分进行数值积分处理。

2.1 球面积分处理

对于球面积分，采用正则单形变换群法，利用正则单形顶点和各顶点中点在球面上的投影作为容积点，以加权和形式对球面积分进行数值计算。其中正则单形顶点正容积点为[4］

取各正顶点中点并投影到球面上，得正容积中点[11］

式中：i ＜l (l=1，2，…，n+1)为正顶点数；n 为状态变量维数；k=n(n+1)/2 为正中点数。取正容积点对应负值作为负容积点正负容积 点 合 集 记 为ai、bk，此 时i=2(n+1)，k=n(n+1)。则式（15）的五阶球面单形积分准则为[11］

2.2 径向积分处理

对于径向积分，采用广义高斯-拉盖尔积分准则对其进行数值计算，首先对式（16）作积分变量替换r= t 使其满足广义高斯-拉盖尔积分形式，则式（16）等价为

采用广义拉盖尔正交多项式对高斯函数进行拟合，罗德里格形式的广义拉盖尔正交多项式表示为

依据拉格朗日插值多项式和带权函数[12］可推得广义高斯-拉盖尔求积权重：

定义1[13］若求积公式

定理1[14］若求积公式

式中：ωj、xj均为未知数，恰当选择其值可使代数精度达2m-1 次。

性 质1[14］插 值 公 式（32）具 有2m-1 次 的充分必要条件是高斯求积节点xj为区间[a，b]上带权函数ρ(x)的m 次正交多项式的零点。

由定理1 可知，五次代数精度需高斯点数为3。由性质1 可知，高斯求积节点为正交多项式的根。由上述条件结合式（30）可得五阶径向积分准则为

式中：tj为式（27）的根。

上文中已得到五阶球面单形积分准则和五阶径向积分准则，结合式（12）、式（19）、式（33）可得处理式（14）的五阶球面单形-径向积分准则：

1）基于PLC的给排水控制系统数据采集，可通过对模拟量数据和数字量数据的科学采集分析，对该系统运行中的控制效果进行科学评估。在此期间，模拟量采集的数据主要有：水仓水位、电机工作电流、水泵轴温度、电机温度和排水管流量。数字量采集的数据主要有：水泵高压启动柜真空断路器和电抗器柜真空接触器的状态、电动阀的工作状态与启闭位置、真空泵工作状态、电磁阀状态、水泵吸水管真空度及水泵出水口压力。通过对这些不同数据的采集，在检测方式的配合作用下，有利于保持给排水控制系统运行中良好的控制效果。

采用准则（19）和准则（34）的滤波算法即为五阶容积卡尔曼滤波。在滤波系统的过程噪声与观测噪声均服从高斯分布的环境下，该算法拥有着高滤波精度，但大多数滤波系统其系统模型均含有如模型误差等非高斯随机变量参与过程噪声影响着系统，所以若想使五阶容积卡尔曼滤波高效应用，则必须要处理这些非高斯过程噪声，下文要讲述的预测滤波就是一种很好的处理方法。

3 预测滤波

预测滤波是基于现有模型与新观测值，利用“协方差约束”条件与代价函数极小值原理对现有模型的模型误差进行矫正得到新的模型，对新模型进行状态方程求解得到状态估计值。

3.1 “协方差约束”条件和代价函数

考虑系统数学模型如下：

式中：x(t)为状态变量；d(t)为模型误差，即为过程噪声；G 为过程噪声系统矩阵；z(t)为观测量；v(t)为高斯观测噪声，假设其均值为0、方差为R。设ẑ(t) 为 预 测 观 测 量，则z(t)-ẑ(t) 为 观 测残差。

定义2[15］若系统观测残差方差阵与观测误差方差阵几乎一致，那么认为系统满足“协方差约束”条件，即

从式（36）～式（39）可知，若系统满足“协方差约束”条件，则状态预测值与状态真值会几乎一致。但若系统观测残差方差阵与观测误差方差阵不一致，说明系统出现模型误差等过程噪声，需要对其进行调整使得系统满足“协方差约束”条件，此为预测滤波的核心要素。模型误差调整量需构造一种代价函数求得。设代价函数为[16］

代价函数呈现为2 个惩罚项之和，其中第1 项为测量残差项，第2 项为模型误差校正项，代价函数跟随测量残差、模型误差和加权矩阵的变化而变化。当代价函数处于极小值时，模型误差调整量有最优解[15］，下文将给出相关推导过程。

3.2 权值矩阵K 讨论

代价函数受d(t)、R、K 和测量残差的影响，而测量残差受d(t)的影响，d(t)又随K 的变化而变化。假设系统最初模型误差相对较大，即最初模型不满足“协方差约束”条件。当K 增大时，代价函数中模型误差校正项较大，此时应减小d(t)。当d(t)减小时，系统趋于原始模型，由于模型误差的原因使得测量残差相对较大，系统不满足“协方差约束”条件。当K 减小时，测量残差项相对较大，观测残差较大，此时应增大d(t)以减小观测残差。但若K 减得很小，即d(t)增得很大，会导致测量残差趋向于0，即预测观测值近似等于实际观测值，此时系统仍不满足“协方差约束”条件。所以K 过大或过小都会对滤波系统不利，合理调节好K 的取值是预测滤波的关键。

3.3 预测滤波原理推导

求取代价函数（40）的极小值，即梯度向量为0

对式（43）截取出现一次d(t)为止：

结合式（42）、式（44）可得代价函数J[d(t)]对d(t)导数：

结合式（41）、式（46）可得模型误差d(t)：

将式（48）所得模型误差代入系统（35）中形成新的系统模型，对新模型的状态方程进行求解即可得到状态估计值。

预测滤波虽然在处理非高斯过程噪声系统中有着很好的表现，但其最终需求解状态方程组来得到状态估计值，这导致其在计算上有一定的复杂度，甚至在高维系统中难以求解，若采用五阶容积卡尔曼滤波方法替代上述求解过程，将2 种滤波算法融合，生成的新算法将以递推形式进行状态估计，从而解决求解问题。

4 预测-五阶容积卡尔曼滤波

预测-五阶容积卡尔曼滤波其核心思想为通过预测滤波方法更新模型误差（过程噪声）建立新的模型，将新模型代入五阶容积卡尔曼滤波器中进行递推状态估计，其算法具体步骤如下：

1） 初始化阶段

初始化参数：x0，K，d0，R，P0。

2） 模型更新阶段

该阶段主要处理非高斯过程噪声对系统的影响，通过读取实际观测数据计算出模型误差调整量，对系统过程噪声及其方差阵D 进行调整，进而得到新的系统模型，新模型将满足“协方差约束”条件。

旧模型：

① 读取实际观测值zk，并计算预测观测值zk|k-1。

② 求解模型误差调整量（48）和模型误差方差阵Dk|k-1，即

注1为相邻n 个时刻中误差调整量d 的均值。

③ 建立新模型：

以下阶段主要处理强非线性滤波问题，采用五阶容积卡尔曼滤波，引入满足“协方差约束”条件的新模型进行状态递推估计。

3） 预测更新阶段

① 对Pk-1|k-1进行Cholesky 分解得Sk-1|k-1

③ 通过状态方程传播状态向量容积点：

④ 一步预测状态值和状态预测误差方差阵：

4） 测量更新阶段

① 对Pk|k-1进行Cholesky 分解成Sk|k-1

注2文献[17］提出了一种矩阵对角化的改进方法，采用该方法可使得方差阵不需要满足Cholesky 分解方法的正定矩阵条件，通过矩阵特征值、特征向量即可构造出满足式（52）和式（57）的矩阵S，此方法很巧妙地避免了系统滤波过程中因矩阵非正定而导致的滤波中断问题。

② 设定观测容积点：

③ 通过观测方程传播观测向量容积点：

④ 一步预测观测值：

以上为预测-五阶容积卡尔曼滤波算法（P5thCKF）的全部步骤，实际程序流程如图1所示。

图1 预测-五阶容积卡尔曼滤波程序流程图Fig.1 P5thCKF flow chart

5 算法仿真验证

本文通过2 个仿真实验对算法进行验证。实验1 采用能代表一般性质的非线性系统验证P5thCKF 算法在强非线性、非高斯过程噪声（非线性模型误差）系统中的可行性；实验2 采用姿态角滤波对带有噪声的飞行器姿态进行滤波，以验证P5thCKF 算法应用于工程实践的可能性。

5.1 实验1

实验1 主要验证P5thCKF 算法应用在强非线性、非高斯过程噪声系统中的可行性，并与CKF、5thCKF 这2 种滤波算法进行对比分析。参考文献[18-19］，设计采用强非线性系统，方程表示如下：

下面列举P5thCKF 算法中，该系统状态空间表示为

式中：d 表示误差调整量；vk表示高斯测量噪声。

式（66）代表一个一般性的非线性系统，实验将以此系统作为实际参照系统，通过3 种滤波方法，对系统4 个状态进行估计。因为系统（66）作为实际系统，所以3 种滤波方法需要对系统（66）进行状态空间表示，然后根据此状态空间表达式进行递推滤波，3 种滤波方法对于系统（66）的状态空间表示相同，但相对于式（66）有着一些结构性的变化，该变化可视为系统（67）因建模原因而造成的非线性模型误差，此误差用以替代系统（66）的非高斯过程噪声。

在仿真模型中分别加入CKF、5thCKF、P5thCKF 这3 种滤波器，对系统（66）进行状态估计。仿真实验中，状态向量的初始值设为

估计误差方差阵初始值为

P5thCKF 的加权矩阵：

模型误差初始值：

测量噪声方差阵设为R=[0.5]。设定仿真步长为0.000 5 s，仿真步数为80，仿真时长为0.04 s，随机选取可行域内不同状态初始值，运行20 次蒙特卡洛实验，最终通过均方根误差（RMSE）[7］对3 种方法进行滤波精度分析。仿真结果如图2、表1 和表2 所示。

表2 各状态RMSE 方差Table 2 RMSE variance for each state

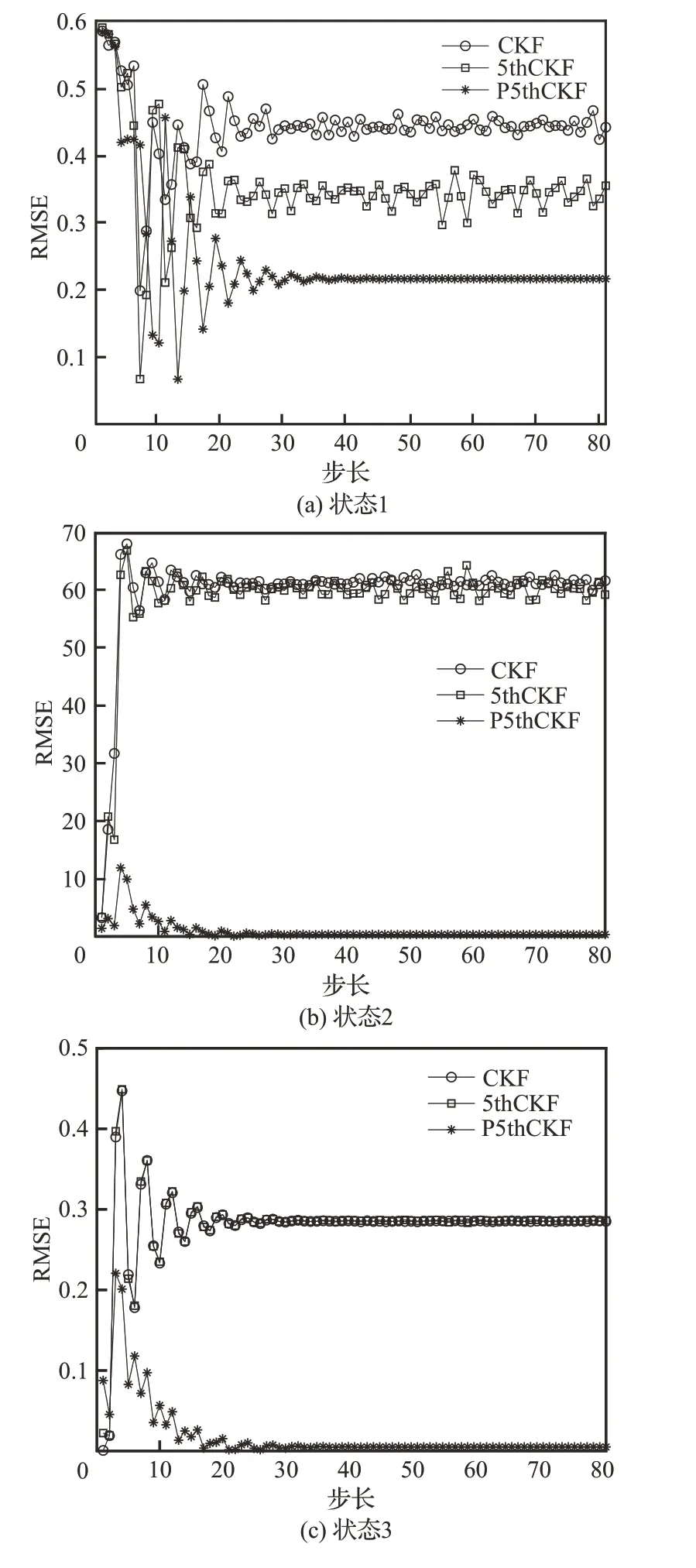
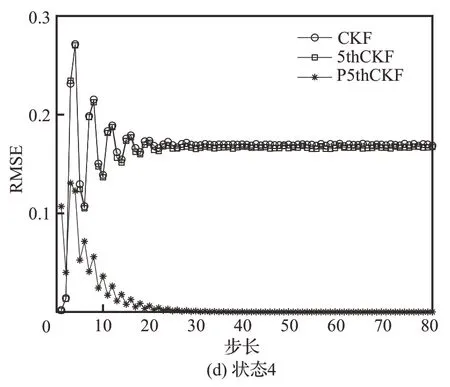
图2 状态1～4 的RMSEFig.2 RMSE for State 1-State 4

对比系统（66）和系统（67）可知，状态3 与状态4 因为三角函数的原因，其全过程输出值应＜1，表1 可以看出CKF、5thCKF 这2 种方法因为模型误差的原因其均方根误差均值处于0.3、0.17左右，而P5thCKF 则接近于0。状态1 因为反正切函数的原因，其本身输出值很大，所以状态3 与状态4 带来的模型误差影响对于状态1 微乎其微，所以3 种方法的均方根误差相差不大。状态2因为缺少了状态1 和乘积因子对其的抑制，使得其估计值会比实际值大1 倍之多，表1 可看出CKF 与5thCKF 对于状态2 的均方根误差均值极大，而P5thCKF 却仅仅为0.48。根据以上分析可以看出，P5thCKF 在强非线性、非高斯过程噪声系统下具有可行性。在4 个状态的估计中，P5thCKF 的估计效果比CKF、5thCKF 的效果要好，而CKF 与5thCKF 之间差距不大，这是因为系统模型不精确而产生的模型误差误导了CKF与5thCKF 这2 种方法估计状态的最终走向，而P5thCKF 因自身带有模型误差校正环节，可根据实际观测量将系统模型误差以调整量的形式回馈给系统本身，所以能使其自调整、更新系统模型以弥补模型误差带来的精度损失。

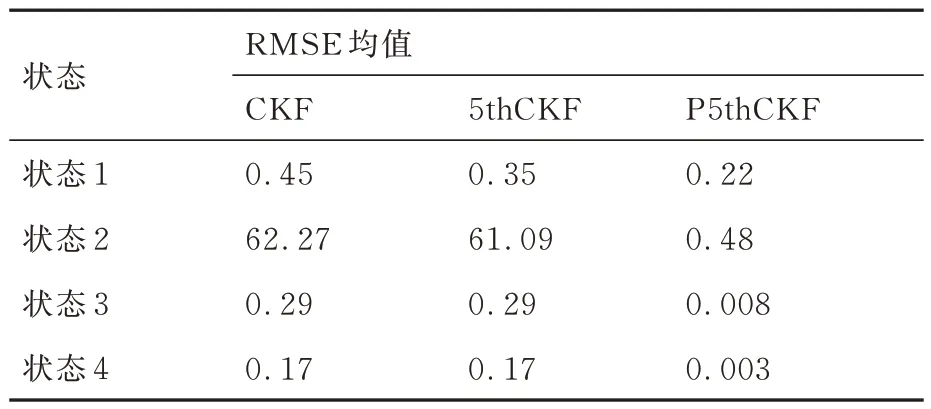
表1 各状态RMSE 均值Table 1 Mean RMSE for each state

5.2 实验2

实验2 采用姿态角滤波以验证本文算法对于工程实践应用的可能性。实验以四元数和陀螺仪角速率为状态变量作状态方程，以加速度计、磁力计输出为观测变量作观测方程，四元数输出值最终转化为欧拉角形式进行比对分析。采用一阶龙格库塔法对连续系统方程进行离散化，系统方程表示如下[20-23］

状态方程：

状态变量x中，q表示四元 数，ω表示陀螺仪角速率；δ表示陀螺仪漂移噪声[24-25］和模型误差等非高斯因素；z表示加速度计、磁力计测得的姿态角四元数；vk表示加速度计、磁力计的测量噪声，本实验假设其为高斯分布。

在飞行器仿真模型中分别加入CKF、5thCKF、P5thCKF 这3 种滤波器，并在陀螺仪角速率输入通道加入漂移噪声和非高斯噪声模块，在加速度计、磁力计输出过程中加入高斯噪声模块，对其进行姿态角估计。仿真实验中，状态向量的初始值为

估计误差方差阵初始值为

P5thCKF 的加权矩阵：

模型误差初始值：

测量噪声方差阵设为

设定仿真步长为0.5，仿真步数为80，仿真时长为40 s，对飞行器模型随机选取输入值以得到飞行器动态变化的姿态角，运行20 次蒙特卡洛实验，每一次实验中，步长20～35 为姿态角动态变化区域，最终通过均方根误差（RMSE）对3 种方法进行滤波精度分析。仿真结果如图3、表3和表4所示。

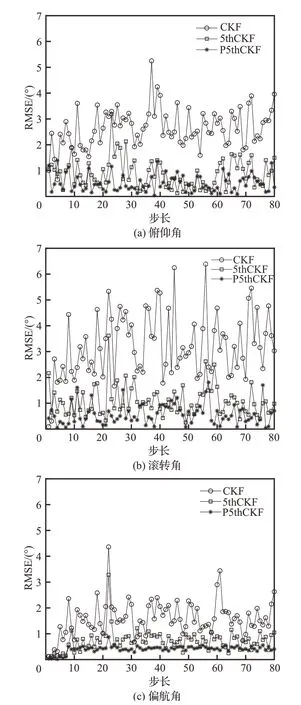
图3 姿态角的RMSEFig.3 RMSE of attitude angle

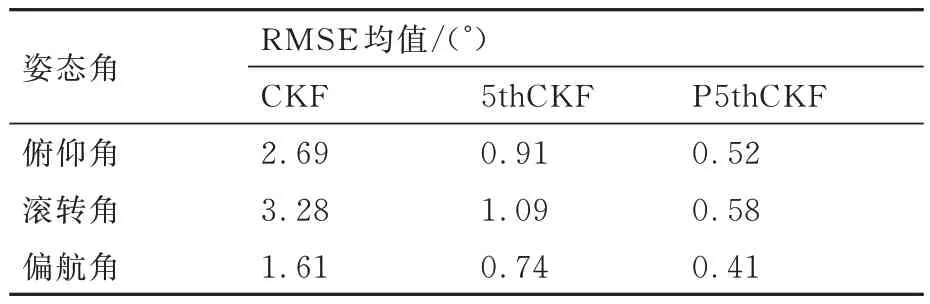
表3 各姿态角RMSE 均值Table 3 Mean RMSE for each attitude angle

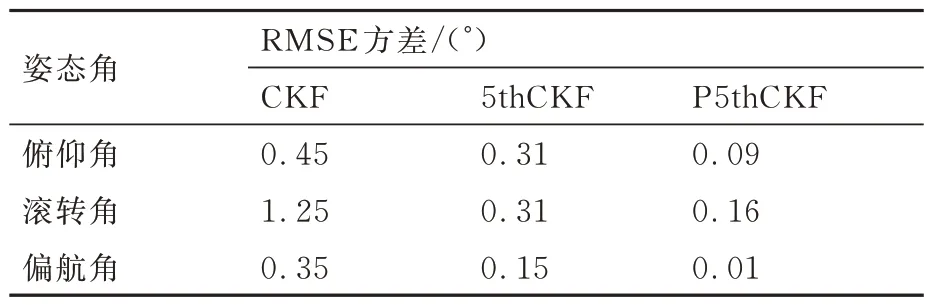
表4 各姿态角RMSE 方差Table 4 RMSE variance for each attitude angle

从工程应用的角度来看，在滤波精度上，由表3 数据可算出，P5thCKF 比CKF 的滤波效果要高约80%，比5thCKF 的滤波效果要高约45%。

在计算量或耗时上，每一次蒙特卡洛实验的算法部分仿真实际时间：CKF 耗时约0.099 2 s，5thCKF 耗 时 约0.117 4 s，P5thCKF 耗 时 约0.120 7 s。在这一次实验中，连续迭代循环调用算法80 次，即3 种算法每一次被调用平均耗时约为0.001 24 s、0.001 46 s 和0.001 5 s，可 知P5thCKF 相较于CKF 和5thCKF 在耗时上增加了约21% 和2.8%。综上，对于CKF 来说，P5thCKF 牺牲了21%的耗时从而得到80%滤波效果的提升，而对于5thCKF 来说，P5thCKF 仅仅增加了2.8%的耗时但换取了45%的提升效果。以上数据也一定程度上说明了本文方法应用于实际工程的可能性。本实验忽略了加速度计、磁力计非高斯测量噪声因素的影响，而是直接假设其服从于高斯分布，使得实验环境趋于理想化，这也是该方法要想应用于实际工程需要重点关注的要点之一，但本文方法因为预测滤波的特性，省去了实际工程应用中需要特别处理的过程噪声或模型误差的过程，仅仅只需考虑测量噪声的处理，这在实际工程量上有了大大的缩减，且一般的工程系统对于过程噪声的考虑与处理要相比于测量噪声要更加复杂，这也体现了本文方法在实际工程应用中的优势。

6 结 论

本文提出了一种预测-五阶容积卡尔曼滤波算法，以应用于强非线性、非高斯过程噪声系统，得出以下结论：

1）P5thCKF 的实质是在五阶容积卡尔曼滤波的框架下用预测滤波的方法对系统过程噪声或模型误差和其方差阵进行实时调整，进而实时递推滤波。其优点是不需要考虑系统中过程噪声和模型误差对滤波造成的影响，而只需考虑测量噪声的性质及其方差即可，大大简化了前提条件。

2）P5thCKF 不仅保证了算法每一次迭代因噪声干扰的系统模型的准确性，而且采用高精度的数值积分准则提高了三阶球面-径向容积积分的代数精度，使得方法更加灵活，精度更高。

3）2 个仿真验证表明，P5thCKF 不管在具有非线性模型误差的系统中还是在非高斯过程噪声干扰下的系统中，其滤波效果都比CKF、5thCKF 更好，且进一步说明了本文方法在强非线性、非高斯过程噪声系统下具有可行性，在应用于实际工程中具有可能性。

4） 本文所涉及到的内容仅仅只是对P5thCKF 方法的提出，而其还有很多内容可进行拓展研究，比如对加权矩阵的模糊动态调整，对七阶卡尔曼滤波进行简化处理，降低计算复杂度以替代五阶容积卡尔曼滤波，将本方法应用于实际工程以考虑各种高斯、非高斯测量噪声的处理问题等。