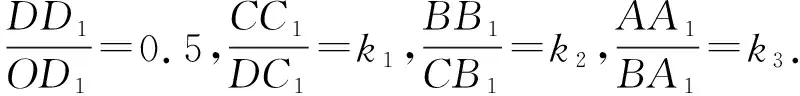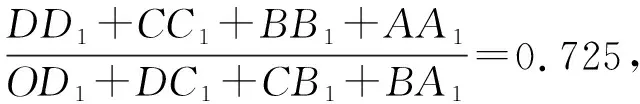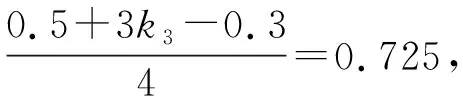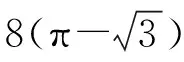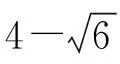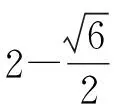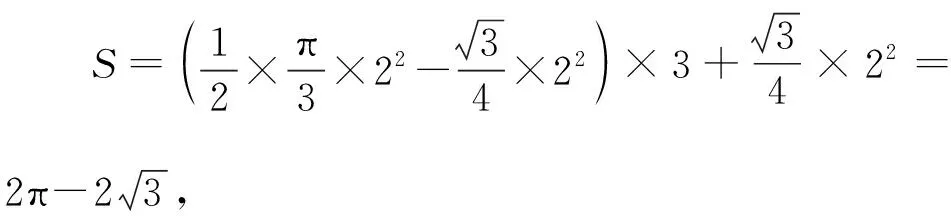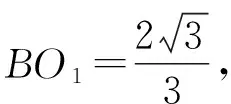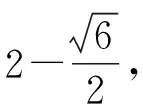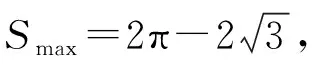变式是金链,模型是核心,突破是关键
——新高考数学建模单元复习的变式思考
陈友兵
(江苏省姜堰第二中学)
2017年制定2020年修改的《普通高中数学课程标准》中有关数学建模核心素养的要求:“能够运用数学建模的一般方法和相关知识,创造性地建立数学模型,解决问题;能够理解数学建模的意义与作用;能够运用数学语言,清晰、准确地表达数学建模的过程和结果”,在数学建模单元复习中,通过挖掘近几年高考数学应用题中的数学模型,引导学生通过现实情境的具体实例,学会中学数学建模的一般步骤:读懂问题,建立模型,求解模型,检验模型.数学建模高考复习的重要途径就是选取经典问题,从不同角度拓展变式,让学生理解数学应用题求解要突破三关:事理关,文理关,数理关,提升学生的数学建模能力.
本文以新高考数学应用题为基本抓手,将函数模型、数列模型、空间图形模型设计变式问题串,通过变式教学掌握数学应用问题的基本模型与建模方法,提升破解数学应用题的能力,通过问题情境教学渗透教育功能,使新高考数学建模复习进入核心素养阶段.
1.中学数学建模步骤与三关突破
1.1中学数学建模方法一般步骤
一是读懂问题情境,包括对题意的整体理解和局部理解,以及分析关系、领悟实质,
“整体理解”就是弄清问题情境所述的事件和研究对象;
“局部理解”是指抓住问题情境中的关键字句,正确把握其含义;
“分析关系”就是根据题意,弄清题中各有关量之间的数量关系;
“领悟实质”是指抓住问题情境中的主要元素,正确识别其类型.
二是建立数学模型,将实际问题抽象为数学问题,数学建模的直接准备就是审题的最后阶段从各种关系中找出最关键的数量关系,将此关系用有关的量及数字、符号表示出来,即可得到解决问题的数学模型;
三是求解数学模型,根据所建立的数学模型,选择合适的数学方法,设计合理简捷的运算途径,求出数学问题的解,其中特别注意实际问题中对变量范围的限制及其他约束条件;
四是检验回归情境,既要检验所得结果是否适合数学模型,又要评判所得结果是否符合实际问题的要求,从而对原问题作出合乎实际意义的回答,这些环节是中学数学应用问题建模的基本构件.
1.2掌握数学建模方法必须突破三关
第一关,事理关,明白数学应用问题情境说了一件什么事,学会数学应用题的建模分析;
第二关,文理关,即阅读理解关,一般数学应用问题的文字阅读量都比较大,通过审题找出关键词和关键句,并理解其数学意义;
第三关,数理关,对问题情境建立的数学模型,会用恰当的数学方法去正确求解并给出实际意义.
2.函数模型
2.1研究目标及背景
根据《普通高中数学课程标准》高考水平测试要求,研究目标是在实际情境中,会根据不同的需要选择恰当方法(图象法、列表法、解析法)表示函数,理解函数图象的作用.
母题选取:
【例1】(2022·北京卷·7)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献,如图描述了一定条件下二氧化碳所处的状态与T和lgP的关系,其中T表示温度,单位是K;P表示压强,单位bar,下列结论中正确的是
( )
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态

(1)事理关,阅读文字与符号和图,问题情境中的变量是温度与压强,研究制冰过程中两者数量关系与制冰状态间的联系;
(2)文理关,通过阅读,发现问题情境中关键词温度与压强,它们之间联系着4个状态;
(3)数理关,通过数字计算T和lgP,在图象中判断4个命题的正确性.
当T=220,lgP=lg1026>3,二氧化碳处于固态,故A选项不正确;
当T=270,lgP=lg128>2,二氧化碳处于液态,故B选项不正确;
当T=300,lgP=lg9987≈4,二氧化碳处于固态,故C选项不正确;
当T=360,lgP=lg729∈(2,3),二氧化碳处于超临界状态,故D选项正确,故选D.
高考数学命题专家设计现实情境,应试者根据情境计算数据,并判断状态情况.由此,函数模型的变式角度,一是问题情境;二是函数模型;三是函数表示方法,一般而言,数学命题专家会在这几个方面寻找命题切入点.
变式方向一:给定指数函数模型,解决现实情境数学问题
变式1:(2020·全国新高考Ⅰ卷·6)基本再生数R0与世代间隔T是新冠肺炎(注:2022年12月26日,国家卫健委发布,将“新型冠状病毒肺炎”更名为“新型冠状病毒感染”.本题为2020年真题,保留原说法,下同)的流行病学基本参数,基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间,在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69)
( )
A.1.2天 B.1.8天
C.2.5天 D.3.5天
(1)事理关,阅读文字与符号,问题情境中的变量是累计感染病例数、时间,研究两者之间的变化规律;
(2)文理关,通过阅读,发现问题情境中关键词为基本再生数,累计感染病例数,指数增长率等;
(3)数理关,抓住指数模型函数进行数据计算、分析与突破.

变式方向二:给定数学化的分段函数,计算图案面积
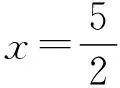
若方程f(x)=a的根的个数为2,则a的取值范围是________;由y=f(x)与y=-f(x)图象所围成的图案面积是________dm2.

(1)事理关,阅读文字与符号,图案已经进行了函数建模并给出了函数表达式;
(2)文理关,通过阅读,发现问题情境中的主干就是函数解析式;
(3)数理关,画出函数y=f(x)的大致图象,如图所示,
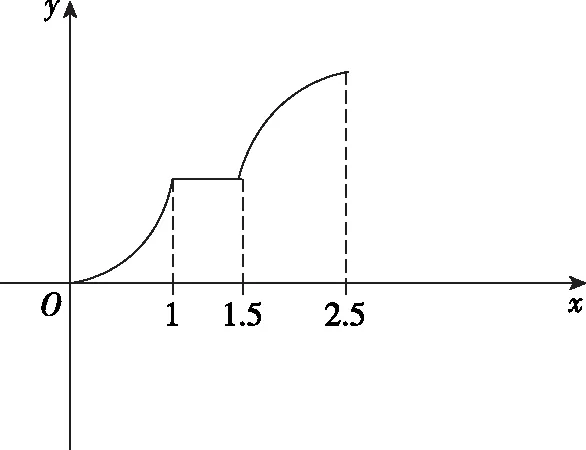
第(1)空,方程f(x)=a的根的个数为2,则a的取值范围是[0,1),(1,2).
第(2)空,利用割补法可知,所求图案面积为一个长方形面积,长为5 dm,宽为2 dm,所以所求图案面积为10 dm2.
变式方向三:给定函数图象,解决现实情境问题
变式3:某游客登高山要乘坐四段缆车才能到达海拔2 970 m的峰顶,海拔高度h(x)(m)与起点水平距离x(m)之间关系图象如图,起点O(0,0),A(100,500),B(200,1 300),C(400,2 100),D(508,2 964),则函数h(x)的表达式是________;如果缆车的行驶速度为6千米/小时,且中间需要三次换乘打卡,每次用时2分钟,则游客从山底到山顶乘缆车需要________分钟.

(1)事理关,阅读文字与符号,问题情境中的变量是海拔高度,水平距离;
(2)文理关,通过阅读,发现问题情境中关键词:海拔高度,水平距离,行驶速度等;
缆车的行驶速度为100米/分钟,所以游客从山底到山顶乘缆车需要30.11+6=36.11(分钟).
变式方向四:融指数模型于情境之中,注重方程求解与检测
变式4:某制药企业为了响应并落实国家污水减排政策,加装了污水过滤排放设备,在过滤过程中,污染物含量M(mg/L)与时间t(h)之间的关系为M=M0e-kt(M0,k是正常数),已知经过1 h,设备可以过滤掉20%的污染物,则过滤一半的污染物需要的时间最接近(lg2≈0.301 0)
( )
A.3 h B.4 h C.5 h D.6 h
(1)事理关,阅读文字与符号,问题情境中的变量是污染物含量与时间,研究两者变化规律;
(2)文理关,通过阅读,发现问题情境中关键词:污染物含量与时间等;
(3)数理关,由经过1 h,设备可以过滤掉20%的污染物,从而确定k,
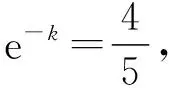
【变式规律及思考】上述问题串说明,变式串主要是对问题情境(现实情境、科学情境、数学情境)、函数模型、函数表达形式(解析式、图象、分段函数等)进行变化,训练复习者对函数概念、方法、思想的理解程度,解决函数模型问题的基本功一是审题、二是运算,重点是分式、指数、对数运算.
3.数列模型
研究目标及背景
根据《普通高中数学课程标准》高考水平测试要求,研究目标如下:
①能在具体的问题情境中,发现数列的等差关系,并解决相应的问题;
②能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.
母题选取:
【例2】(2021·上海卷·19)已知某企业今年(2021年)第一季度营业额为1.1亿元,以后每个季度的营业额比上个季度增加0.05亿元,该企业第一季度的利润为0.16亿,以后每季度比前一季度增长4%.
(Ⅰ)求2021年起前20季度营业额的总和;
(Ⅱ)请问哪一季度的利润首次超过该季度营业额的18%?
引导学生参与市场经济活动,突出数列基本运算.
(1)事理关,阅读文字与符号,问题情境中的变量是营业额、利润、增长率;
(2)文理关,通过阅读,发现问题情境中的营业额、利润、增长率之间的联系;
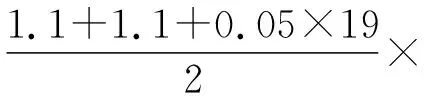
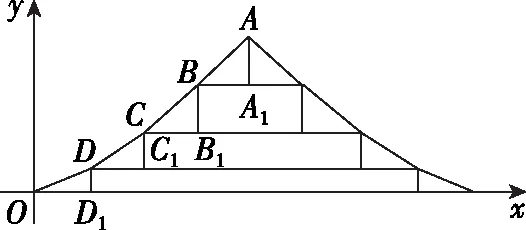
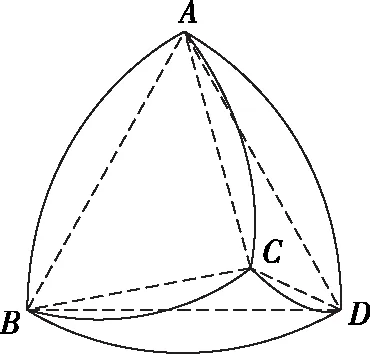
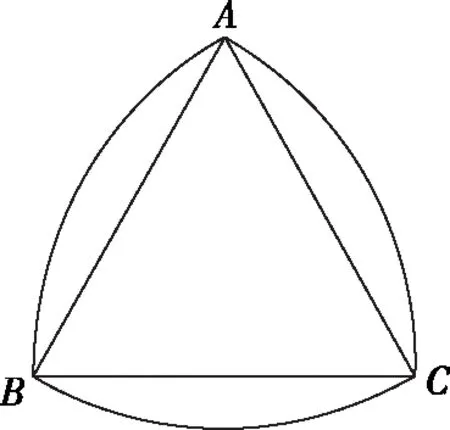
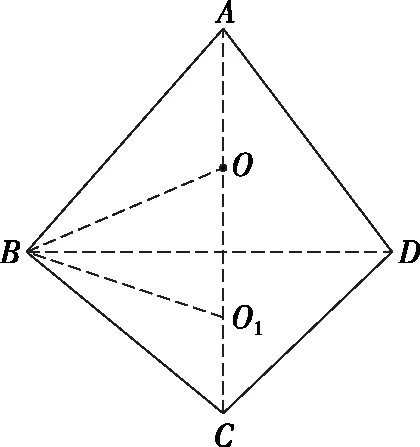
(Ⅱ)设2021年起,第n季度(n∈N*)营业额为an,则an=a1+(n-1)d=0.05n+1.05,设第n季度利润为bn,则bn=b1qn-1=0.16×(1+4%)n-1,an×18% 命题专家对于数列模型的变式角度,一是问题情境变化——寻找活的贴近时代的热点;二是数列类型变化;三是数列表达形式变化,但核心之一就是渗透教育功能. 变式方向一:改变问题情境形式,突出数列(函数)拟合 变式1:某大江截流电视直播,从上午9点开始,当时龙口水面宽40米,水深若干米,每隔一段时间播音员报告龙口的水面宽和工程进展情况,现记录部分分段公布的数据如下, 时间9点10点11点12点…16点龙口宽40米39米…34米…工程进度1米…5米…数据列a1…a2+a3… 预计下午4点(16点)合拢,现根据截止12点的部分数据. (1)学生甲将工程进度模拟成等差数列,a1=1,a2+a3=5; (2)学生乙将工程进度模拟成等比数列,a1=1,a2+a3=5. (1)事理关,阅读文字与符号,问题情境中的数据(龙口宽与工程进度)间关系是什么,可以用什么数列(函数)去拟合; (2)文理关,通过阅读,发现问题情境中关键词是龙口宽(米)与工程进度(米),时间等; (3)数理关,学生甲的模拟预测方法:将工程进度{an}模拟成公差为d的等差数列,由a1=1,a2+a3=5,得2a1+3d=5,所以d=1,所以S7=7a1+21d=28<40,这说明按甲的模拟预测不能如期合拢; 变式方向二:渗透数学文化,突出数学解模 变式2:高斯是德国著名数学家,享有“数学王子”的称号,他最早提出用[x]表示不超过x的最大整数,因此人们称f(x)=[x],x∈R,为高斯函数,已知数列{an}满足a1=1,且(n+1)an+1-nan=2n+1,若bn=[lgan],数列{bn}的前n项和为Tn,则T2023= ( ) A.4 956 B.4 959 C.4 962 D.4 965 (1)事理关,阅读文字与符号,问题情境中的取整函数,一般学生会有所了解; (2)文理关,通过阅读,发现问题情境中有两个数列间关系,研究后一数列前n项和; (3)数理关,问题的主干是“(n+1)an+1-nan=2n+1”, 为了运算简洁,作变换令cn=nan,则cn+1-cn=2n+1, 由c1=a1=1,c2-c1=3,…,cn-cn-1=2n-1,累加可得cn=n2,n≥2. 当1≤n≤9时,bn=0;当10≤n≤99时,bn=1; 当100≤n≤999时,bn=2;当1 000≤n≤2 023时,bn=3, 所以T2023=9×0+90×1+900×2+1 024×3=4 962,故选C. 【变式规律及思考】数列也是函数,命题专家收集现实情境中新颖的能够联系教育功能的案例,以等差数列、等比数列模型为基础,多种形式呈现,因此,变式角度非常丰富,着力检测学生的创新思考的意识. 研究目标及背景 根据《普通高中数学课程标准》高考水平测试要求,研究目标如下:知道球、棱柱、棱锥、棱台的表面积和体积的计算公式,能用公式解决简单的实际问题. 母题选取: ( ) 图1 图2 A.0.75 B.0.8 C.0.85 D.0.9 (1)事理关,阅读文字与符号,看懂问题情境中古建筑物的剖面图,举与步是什么; (2)文理关,通过阅读,发现问题情境中OA斜率与各相邻桁斜率间的数量关系; (3)数理关,设OD1=DC1=CB1=BA1=1,则CC1=k1,BB1=k2,AA1=k3,依题意可得方程, 变式方向一:改变问题情境,关注教育功能 变式1:资料表明,2021年某小麦主产区收获的小麦为9×1010kg,为了收购储存这些小麦,需建设n(n∈N*)个粮仓,每个粮仓是直径为10 m,高5 m的圆柱和底面直径为10 m,高3 m的圆锥组成的,每立方米空间可以储存0.9×103kg小麦,则n至少是________(π≈3.141 592 6). (1)事理关,阅读文字与符号,问题情境中的变量是小麦仓储中粮仓体积与个数; (2)文理关,通过阅读,发现问题情境中关键词圆柱与圆锥的粮仓体积; 变式方向二:创设复杂问题情境,突破综合分析障碍 变式2:勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动(如图1),利用这一原理,科技人员发明了转子发动机,勒洛四面体是以正面体的四个顶点为球心,以正四面体的棱长为半径的四个球的相交部分围成的几何体,如图2,若正四面体ABCD的棱长为2,则下列说法正确的是 ( ) 图1 图2 (1)事理关,阅读文字与符号,问题情境中组合几何体的分解; (2)文理关,通过阅读,发现问题情境中关键词有截面面积,内切球半径,正四面体等; (3)数理关,学会将组合体分解, 对于A,该人圆面体的截面示意图如图1,所以 对于B,由对称性知,勒洛四面体ABCD内切球球心是正四面体ABCD的外接球球心O,如图, 设正四面体ABCD的外接球的半径为R, 故选CD. 图1 图2 【变式规律及思考】以空间模型为载体的数学建模的数学应用题是近两年高考数学命题的热点,由于空间几何体的基本类型多,现实生活中情境也多,所以高考命题变式方向也多样,文中变式串由易到难,改变情境,贴近现实.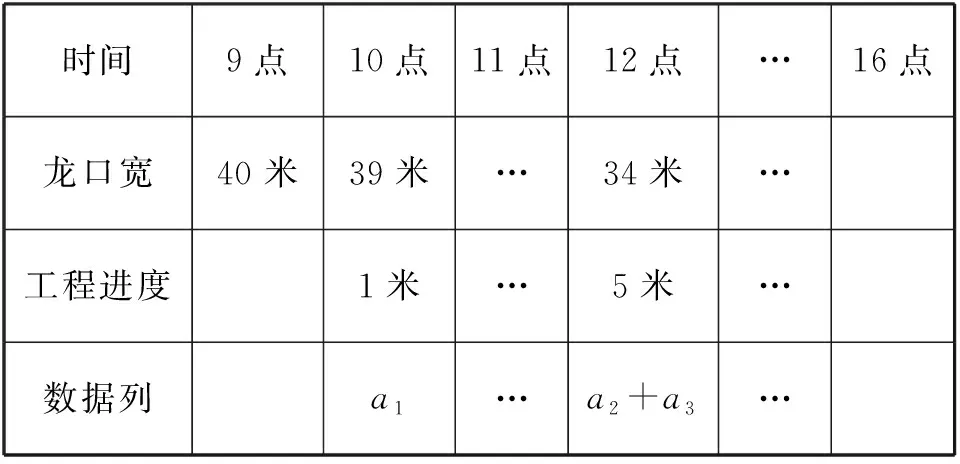

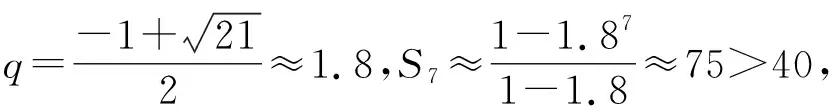
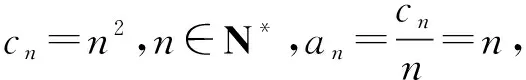
4.空间图形模型