船舶起重机主辅臂分级补偿的虚拟约束控制策略研究

陈英龙,车思儒,宋甫俊,弓永军

(1.大连海事大学 船舶与海洋工程学院, 辽宁 大连 116026;2.流体动力与机电系统国家重点实验室, 杭州 310027;3.海底工程技术与装备国际联合研究中心, 辽宁 大连 116026)

深海起重机为了确保将货物安全高效地转移,需要设计控制器对起重机随环境外力的运动进行补偿控制。迄今为止,起重机吊物消摆常见的控制方法有:延迟反馈控制、PID控制、输入整形控制、主动补偿技术、滑模控制、鲁棒控制、模糊逻辑控制和神经网络等。由于实际应用中起重机工况和类型的不同,基于上述控制方法科研人员发展出来各种具有特殊性的起重机补偿方案。

目前国内常见的研究主要是对2自由度起重机的消摆,由于吊物的摆动角度大小受到吊点位置变化影响,通过仿真研究各种控制器对吊机消摆效果。张小亨[1]建立了工作船运动时的深海起重机运动学模型。运用Matlab/Simulink软件建立了系统的仿真模型,对母船2种不同运动情况下的主动补偿控制效果进行对比。这种简化消摆方案与实际应用有较大出入,存在着较大局限性。因此,袁枞[2]考虑实际缸和电压信号之间关系,结合模糊控制方法确定吊物摆动控制电压的实际值,通过船用起重机转台回转和吊臂变幅控制摆动。受条件限制,在真实的起重机上开展控制策略对吊钩消摆作用的研究是非常困难的。因此,如何实现更加贴近实际场景开展补偿控制策略是当前的研究热点之一。蔺本浩[3]通过Solidworks和Adams软件进行联合建模,在Adams模型中进行了吊臂柔性化等工作,搭建了船用起重机虚拟样机模型。最后基于虚拟样机设计消摆PID控制器,实现了较好的消摆效果。然而,其对海浪的运动情况的研究中,将海上规则波的波面运动转化为数学激励,未考虑恶劣海况下不规则波的影响。

在过去的几十年里,国外研究人员对船载起重机的控制开发了几种防摇控制方法。2001年,Henry等[4]创建了一种延时反馈控制器,能够为海上起重机吊臂保持所需的世界框架位置,并由Masoud等[5]扩展为旋转吊臂起重机。2002年,Agostini等[6]还开发了一种控制系统,能够保持旋转臂起重机有效载荷的世界框架位置。2005年,Suthakorn等[7]为海上吊臂起重机开发了抗摇控制器,并且只考虑了船舶的俯仰和偏航运动。2011年,Ngo等[8]考虑了一种4自由度集装箱起重机,并开发了一种使用PD控制器和轨迹修正器的防摇控制器,以保持有效载荷的世界框架位置,随后在2012年开发了一种滑模控制器[9]。2013年,Ismail等[10]为海上吊臂起重机和旋转吊臂起重机开发了二阶滑模控制器,Rauh等[11]为安装在具有2个自由度模型的船舶上的吊臂起重机开发了滑模控制器。2015年,Ismail等[12]为海上集装箱起重机开发了一种鲁棒滑模控制器,目的是处理不确定扰动,如阵风。Ngo等[13-14]开发了一种用于3自由度海上集装箱起重机的模糊调谐滑模控制器,而Qian等[15]开发了一种用于海上吊臂起重机的非线性学习控制器。2018年,Frikha等[16]提出了一种用于3自由度(DOF)龙门起重机的自适应神经滑模控制器,并在仿真中表明,该系统能够在吊绳长度变化的情况下跟踪期望的轨迹。Singh等[17]开发了一种用于2自由度龙门起重机的分数模型预测控制器,2019年,Maghsoudi等[18]将基于神经网络的输入整形器应用于5自由度龙门起重机,并展示出显著的减摇效果。对于船载起重机,除了陆基起重机的跟踪控制问题外,起重机基座本身也随船移动,进一步激励有效载荷,特别是在甲板作业已经很危险的状态下,意外的有效载荷运动会造成严重的危险。

精确控制任何起重机的有效载荷是一个复杂的控制问题;有效载荷的移动会对附近工作的人造成危险,或者可能会对有效载荷本身或周围环境造成损害。起重机的欠驱动、非线性系统、有效载荷的稳定控制是一项具有挑战性的任务,因此引起了研究界的极大关注。

本文基于一种高效率、高精度、响应快的3自由度悬臂补偿机构,提出了一种基于虚拟约束的起重机主臂-辅臂分级补偿控制策略,实现恶劣海况起重机转运作业补偿。针对传统船用起重机控制设备结构复杂、本体惯性重、响应频响慢的问题,设计了新型的3-DOFs主臂串联3-DOFs辅臂起重机模型,起到可补偿起重机工作范围大及小范围的高精度响应快的补偿效果。通过建立起重机主臂的PID控制器以及辅臂的速度补偿控制器,在四级海况仿真条件下验证提出的新型补偿机构以及补偿控制器能够显著提升恶劣海况下船舶起重机的吊物的平稳性,补偿率可以达到75%,扩大了船舶起重机可作业环境区间,验证了分级补偿策略的有效性。

1 辅臂3自由度机构设计

海上船舶起重机受到风浪影响,吊重移动会对附近工作的人造成危险,因此设计了一种新型的3-DOFs主臂串联3-DOFs辅臂的起重机模型,提高起重机的控制能力。深海起重机的主臂带有1个回转自由度和2个自由度俯仰,变幅范围大;而辅臂具有1个伸缩自由度、2个回转自由度,悬挂在大臂末梢部位的一侧,变幅范围小。该起重机中主臂具有调节范围大,但响应慢,实时跟踪精度不高;而辅臂则相反,其调节范围小,但响应快,实时跟踪精度较高,如图1所示。

图1 海上起重机及末端辅臂联合示意图

船用起重机增加辅助臂的目的并不是取代其原有主吊臂的大重量起重转运功能,而是在保证原有起重机起重大吨位货物的同时,又可以做到小重量货物的精确安全转运。起重机辅助臂结构主要转运的目标物是转运人员或者精密容易损坏的货物等重量较轻的物品,通过设计的新型辅助臂结构减小船舶随恶劣海况下的货物摇晃,提高转运安全性。

起重机消摆通过主臂加辅臂的结构设计,实现主臂约束、辅臂跟踪的分级补偿控制。主臂采用基于PID控制的补偿方案,利用转盘回转运动及臂架变幅运动调节吊重位置,增大调节范围。辅臂采用基于速度补偿技术,通过变幅液压缸改变辅臂的侧摆、俯仰角度及伸缩长度实现吊重调节,具有响应快、实时精度高的优点,如图2所示。

图2 起重机末端辅臂结构示意图

考虑到恶劣海况的影响,结合主臂与辅臂的优势,提出了基于虚拟约束的分级补偿控制策略,实现高效率、高精度的转运消摆控制。分级补偿控制策略既增大起重机的调节范围,又保证系统的高响应和高补偿精度,使消摆时间缩短15%,能够更稳、更准地解决恶劣海况下转运的消摆补偿问题。

1.1 运动学

船舶随海浪的运动会给船舶起重机操作带来多方向的运动。船舶的横摇、升沉、纵摇的艏摇等,会带动起重机运动,从而导致负载发生不必要的位移和旋转运动。这些意外的运动会导致危险的碰撞、缆绳故障以及起吊和卸载操作中的不当风险。通过机器人运动学中的D-H方法建立船用起重机系统的运动学模型,建立4个相应的坐标系,世界坐标系S-XYZ、船体坐标系C-XCYCZC、起重机主臂坐标系Q-XQYQZQ、起重机辅臂坐标系F-XFYFZF。

根据图3建立起重机的连杆坐标系,设基座坐标系Q-X0Y0Z0为{0}系,其原点为Base点。主吊臂的回转关节坐标系c-X1Y1Z1为{1}系。俯仰关节坐标系d2-X2Y2Z2为{2}系。e-X3Y3Z3为主吊臂末端关节坐标系,即{3}系。当2个关节角为0时Z2轴和Z3轴均垂直纸面向外。辅吊臂同样具有3个自由度,回转关节坐标系g-X4Y4Z4,即{4}系。此外,辅臂的俯仰关节坐标系h-X5Y5Z5的自身运动范围也受到一定限制,起到补偿大臂俯仰运动的作用。而辅臂的末端关节是一个伸缩缸构成{5}系,达到小范围调节末端位姿的作用。此时建立的坐标系示意图如图4所示,起重机连杆坐标系选取如图5所示。

图3 地面系、船体系和起重机坐标系示意图

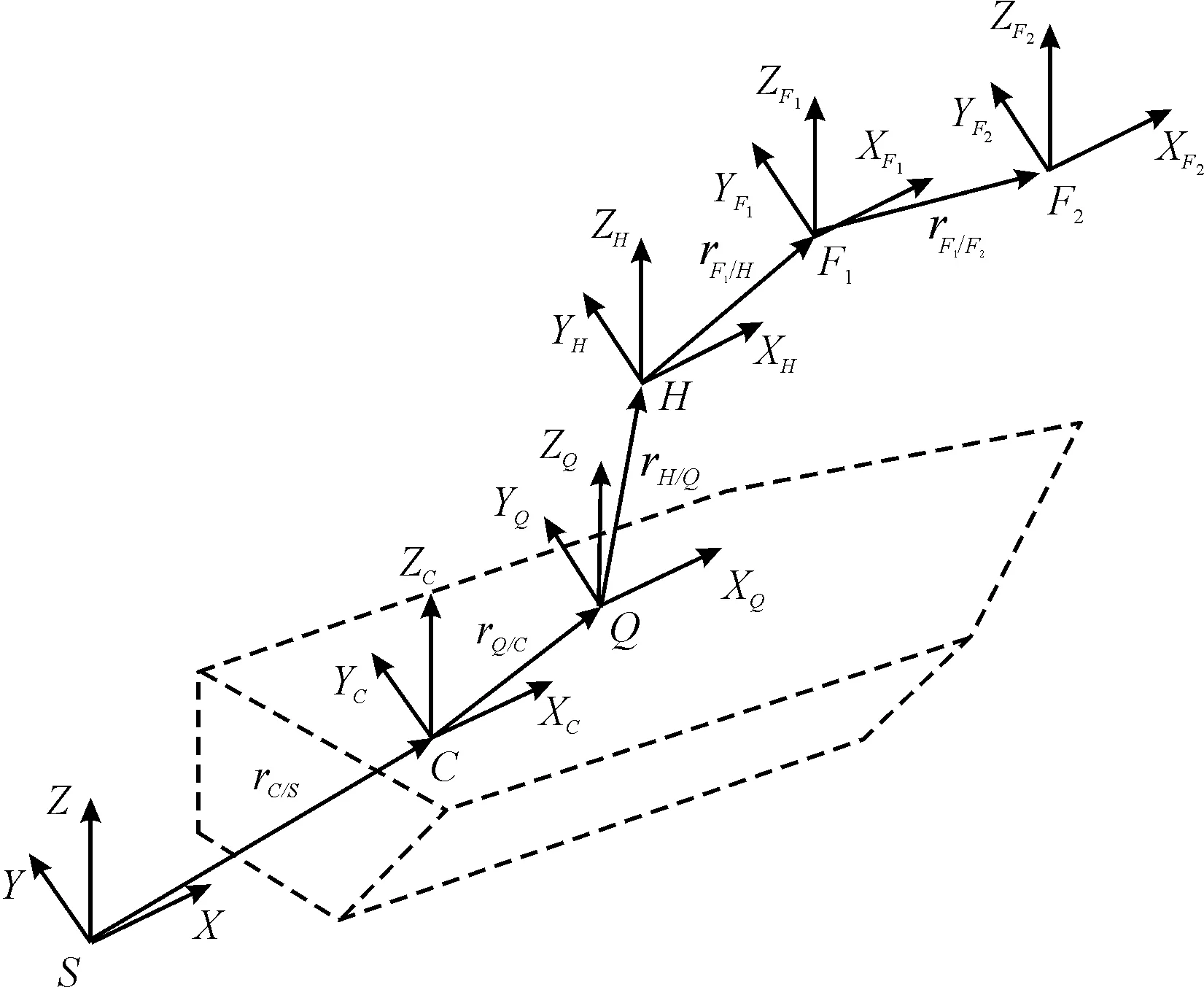
图4 地面系、船体系和起重机主臂坐标系示意图

图5 起重机连杆坐标系的选取

根据起重机连杆坐标系可以列出如表1的D-H模型参数,其中吊臂长度为L,a表示铰接点距离起重机机身回转轴线的长度。

表1 主臂D-H模型参数

根据表1中的参数以及转换矩阵公式可得回转关节坐标系到基座坐标系的转换矩阵。

根据表2中的参数以及转换矩阵公式可得各坐标变换矩阵。

表2 辅臂D-H模型参数

由于辅臂系{F}相对于主臂第3个关节坐标系{3}为绕x轴旋转pi/2,且沿着x轴偏移Lb,那么,辅臂坐标系{3}到坐标系{4}的转换矩阵为:

(1)

(2)

(3)

起重机系原点Q在船体系{C}中的坐标可以用(Bx,By,Bz)表示,(dx,dy,dz)是起重机基座底部平面中心点在船体系中的空间坐标,H是吊臂距离底部基座的垂直距离,则起重机系原点在船体系中的坐标为:

(Bx,By,Bz)=(dx,dy,dz)+(0,0,H)

(4)

(5)

最末端坐标系{6}到地面系{S}的转换矩阵,需要将得出的转换矩阵连续相乘。

(6)

(7)

其中(bx,by,bz)表示吊臂末端在地面系中的坐标。经计算可得:

(8)

3×3 矩阵的rij(i,j=1 2 3)表示坐标系{6}对于地面系{S}的姿态矩阵。

1.2 动力学建模

1.2.1拉格朗日方程动态模型

拉格朗日方法是一种非常实用的系统分析工具,尤其适合解决变量多、耦合复杂的动力学系统。计算出系统的相对动能与惯性力的做功情况,建立系统的动态模型。在本模型系统中相对动能为旋臂动能与负载动能和。根据以上分析,即可计算得到各变量的具体表达式。以上起重机动力学模型可以整理为

(9)

等效惯性矩阵

M(q)=MA(q)+MB(q)

(10)

(11)

(12)

1.2.2吊物动力学模型及搭建

吊物在运动过程中,可以得知当前初始位置和运动速度,通过动力学计算出恶劣海况下受船体自身运动影响的实时变化,即到下一运动时刻吊物位置的变化,并获得吊物动力学响应。基于牛顿欧拉法的吊物动力学模型表达式如下所示:

(13)

(14)

通过状态分量可分别表示为:

(15)

(16)

(17)

式中:k为绳索的刚度;b为阻尼;x为吊物的状态变量,(x1,x3,x5)分别为吊物xyz轴的位置,(x2,x4,x6)分别为吊物的速度;l0为初始绳长。

2 基于虚拟约束的主臂-辅臂分级补偿控制

2.1 虚拟约束

恶劣海况对吊物的影响是极为可怕的,传统的多自由度起重机由于自身惯性大等原因存在响应慢、跟踪误差大的问题。因此,单纯依靠PID控制或者速度补偿反馈等传统控制策略不能满足补偿要求。本文提出一种基于虚拟约束的分级补偿策略,结合设计的主辅臂起重机系统,实现恶劣海况下的吊物补偿,基于虚拟约束的方式实现主臂缩小补偿范围,辅臂精准补偿,提高跟踪频响,减小误差。如图6所示,分级补偿主要分为两部分:其一,通过PID控制将主臂限制在靶位约束区域S内,即末端点P′∈S;其二,在虚拟约束范围内根据速度补偿技术对吊物坐标P实现准确的定点补偿,此时主要是辅臂起到关键作用。

图6 基于虚拟约束的分级补偿控制示意图

采用相应的方法[19]的基本思想是在机器人工作空间中构造一种虚拟势场,目标点产生“引力”,障碍物产生“斥力”,从而对机器人的运动加以引导和限制。

由引力势场函数对距离求导可得引力,如下所示:

fa=ξ(Pti-Pti-1)

(18)

t时刻以及前一时刻的轨迹点坐标分别用Pti、Pti-1表示,Pt=[x,y]T;机器人在势场中会受到引力fa。

根据上述势场的数学公式以及斥力场的数学模型,斥力数学的数学模型如下:

(19)

式中:末端点Pti距离约束区域Ft的值为ρtool,势场作用的最大距离为ρmax,机器人在势场中的受力为fr。为了避免产生的排斥作用过大,在虚拟约束区域外还设置安全距离ρmin,当ρtool<ρmin,fr=fmax,为可以接受的斥力边界。

当吊物处于约束区域S外时,受到引力fa作用,引导起重机系统调整输入使吊物能够接近约束区域S内;当吊物处于约束区域内S时,受到斥力fr作用,促使起重机系统调整输入使吊物能够处于约束区域S内。

根据约束要求,定义禁止区域S为在点P0为中心,长径R1,短径R2的柱体部分,虚拟约束区域部分的数学形式如下:

(20)

由于实际转运过程中吊物受到的恶劣海况影响变化多端,不变的虚拟约束区域F并不能满足海上恶劣情况,提出一种随起重机末端位置姿态Pti变化的约束区域St。约束区域St斥力场的数学模型如下:

(21)

(22)

(23)

(24)

式中,R1(0)=R2(0)=R(0)为X、Y方向最小约束范围。

2.2 主臂PID补偿控制

针对起重机主臂摆动情况,将消摆分为2个部分:回转消摆和俯仰消摆。面外角[20]为起重机吊钩垂直于吊臂与回转中心所构成的平面摆动产生的角度;面内角是吊钩平行于吊臂与回转中心所构成的平面摆动产生的角度。由此可知,面外角可以通过回转运动来调节,面内角则可以通过俯仰运动来调节。

回转消摆解决了面外角的补偿问题;俯仰消摆解决面内角的补偿问题。根据文献可知,面内角的幅度小于面外角摆动幅度,在控制面外角的同时面内角也能得到抑制。因此,主要抑制的是面外角,在对面外角消摆的同时也能够帮助抑制面内角。PID控制系统原理如图7所示。

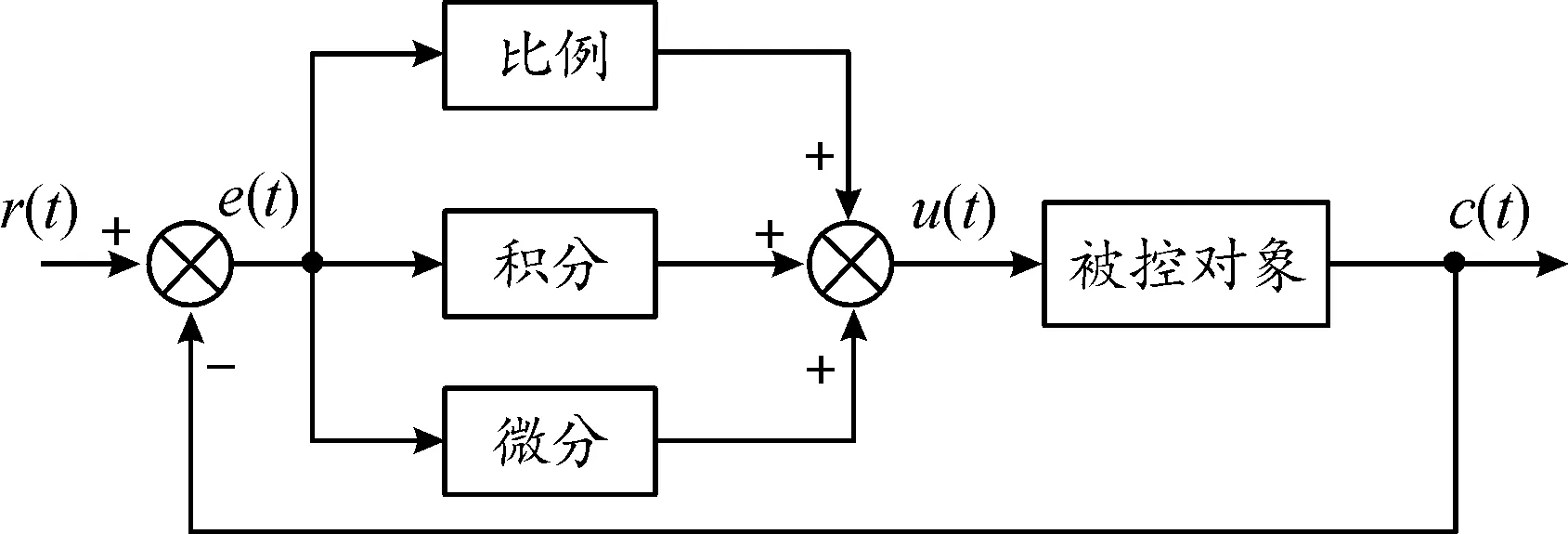
图7 PID控制系统原理示意图

控制量u(t)表达式为:

(25)

传递函数表达式为:

(26)

式中:Kp为比例系数;Ki为积分时间常数;Kd为微分时间常数。

2.3 辅臂速度补偿算法

补偿起重机关节角速度,需要对吊臂整体的运动方程求微分。起重机辅助吊臂部分在世界坐标系下6个方向的速度是由起重船舶的运动情况、起重机所有关节的角度相互耦合形成的。

sγcαsβ+a2cαcβ+d2sα

(27)

Lsδcγcαsβ+sγcβcα+Lsαcδsζ+

Lcδcζcαcβcγ-sγsβcα

(28)

(29)

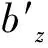
sβsγ+Lcδcζsγcβ+sβcγ

(30)

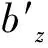
v=Lbcβcγ-Lbsβsγ+cγcβ-sγsβ+a2cβ+

Lcδcβcγ-Lsδsβcγ-Lsδcβsγ+

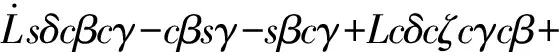
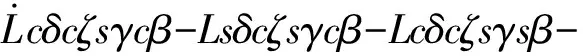
Lcδsζsγcβ+cβcγ-sβsγ

(31)

3 基于虚拟约束的主辅臂仿真分析

分别对起重机系统做PID控制仿真和速度补偿控制仿真,获得4级海况下起重机末端的控制前后状态以及吊物的控制前后状态。对结果进行对比,验证控制方法的优越性。

3.1 无补偿下转运过程仿真结果

对起重船施加4级海况下的波浪荷载,波高4～8FT(1.25～2.50 m),波浪具有明显的形状,得到起重机系统的6自由度响应时程如图8所示。

图8 恶劣海况下船舶的6自由度响应时程曲线

施加4级波浪荷载主要是针对船舶在锚定时候遇到恶劣海况进行船舶货物及人员转运,所以船舶起重机系统在波浪激励下在X方向趋于稳定,变化不是很显著;在Y方向的变化比较明显,变化值在14 m左右;在Z方向的变化范围在1.2 m左右;横摇纵摇因为输入很小也是趋于稳定在1°左右,艏摇最大在28°左右。

在此工况下计算吊物各方向位移及偏离平衡位置的距离(如图9),吊物在X方向上基本稳定,Y方向上最大位移是4.5 m,Z方向的位移变化最大是2.8 m。

吊物的偏离平衡位置、摆角及动力放大系数的变化如图10所示。吊物的偏离平衡位置最大距离是4.3 m,最大摆角是77.3°,最大伸长倍数在1.55倍左右。

图9 无补偿状态吊物各向位移曲线

图10 无补偿状态偏离平衡位置、摆角和动力放大系数曲线

从图10可以看出,吊运物体的摆角最大为77.3°,与稳定位置的距离最大值为4.3 m,同时在船体竖直方向上的位移偏差最大为2.8 m,吊运物体随着风浪而产生晃动,吊索也会随着伸长,吊索受力最大时伸长了1.55倍,常规的吊索很难有如此高的形变量,极易产生断裂,发生危险。

综合以上对无补偿状态下船体运动引起的吊运物体动力响应分析,转运吊物因恶劣海况的移动会对附近工作的人造成危险,或者可能会对吊物本身或周围环境造成损害。

3.2 补偿控制前后对比分析

对起重机系统做联合补偿控制仿真,获得4级海况下起重机末端的控制前后状态以及吊物的控制前后状态。

如图11所示,图11(a)—(c)是分级补偿控制后起重机末端的位置变化,可以看出除初始的振动,末端的坐标最后趋于平稳。图(d)—(e)中末端稳定于坐标(-27.660 6,1.608 2,29.600 2),对比平衡位置,X、Y、Z轴的误差分别为0.019 4、0.007 8、0.38 m。

图12(a)—(c)表示吊物的状态变化,吊物的坐标最后稳定在(-27.645 8,1.551 1,24.887 9),由于绳长5 m,忽略绳长变形,X、Y、Z轴的误差分别为0.035、0.096、0.66 m。

在此工况下计算吊物各方向偏离平衡位置的距离如图12(d),起重机吊物的摆角的变化如图12(e),钢丝绳的动力放大系数如图12(f)。从上图可以看出,控制后吊物的最小摆角达到了0.02 rad,偏离平衡位置的距离逐渐衰减,低于1 m,这给吊物的就位减轻难度,降低起重船的安全隐患。由于补偿效果的增强,吊索的伸长倍数最大值为1.000 5,长度形变非常小。综合以上对动力响应的分析,分级补偿控制对吊物的消摆和升沉补偿有效,使其能够在复杂海况下安全工作。

图11 补偿控制前后起重机末端状态曲线

图12 吊物的补偿控制前后状态曲线

如图13(a)所示,受到虚拟约束的影响,末端吊物超出设定补偿边界范围时(即在受到突然的环境外力时),会产生约为7 kN的虚拟约束力,经过控制器控制信号调节,在短时间内迅速恢复到稳定状态。当吊物末端一直处在虚拟约束边界区域,则一直受虚拟约束力,并随着末端运动趋势向外而增大,如图13(b)所示。

仿真结果表明:提出的新型补偿机构能够显著提升恶劣海况下船舶起重机吊物平稳性,补偿率可达75%,扩大了船舶起重机可作业环境区间。

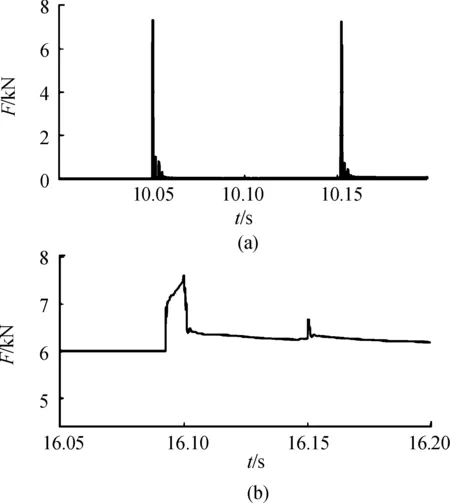
图13 吊物调节阶段性外力的能力曲线

4 结论

下一步研究工作将搭建起重机补偿机构缩比实验平台,结合分级补偿的控制方法以及6自由度平台模拟海况变化,将实际恶劣海况作为起重机减摇防摆过程的起始输入,提出进一步的解决方案。