车辆质点系交通流参数描述及仿真分析
储江伟,韩媛媛,李 红,刘梓敬,李宏刚
(东北林业大学 交通学院, 哈尔滨 150040)
交通流的研究旨在揭示个体交通参与者与由此产生的交通流动态之间的关系。英国学者Lighthill、Whitham[1]和Richard[2]提出基于流体力学中的相关参数对交通流运行状态定量表述方法,通过交通流的三参数(交通量、速度、密度),利用流体力学的质量守恒连续性方程,构建了LWR模型,此模型再现了当时大量的真实交通现象。Munjal等[3-4]将该模型拓展到多车道,对每个车道应用LWR模型。Zhang[5]以及Chanut等[6]都针对交通流中车辆速度差异性以及车身长度等的交通流各向异性的特征对LWR模型进行相应拓展。秦严严等[7]得到混有协同自适应巡航控制车辆的混合交通流LWR模型。但是由于假设车流速度与密度满足平衡速密关系,LWR模型不能描述实际交通流中迟滞以及非线性宏观交通流现象。Waong等[8]考虑个体驾驶者在速度选择方面的差异性对LWR模型进行改进,验证了所提模型能描述交通流迟滞等宏观特性。Ngoduy等[9]针对LWR模型的不足通过近似表达黎曼解算子,提出了多车种一阶宏观模型。Daganzo[10-11]将LWR模型离散化建立了研究动态交通问题的元胞传输模型。Payne[12]将流体动力学的动量引入Newell[13]所提出来的跟驰模型,用流体力学的动量方程代替得到高阶交通流模型,该模型可以分析交通流的失稳引起时停时走现象。Zhang[14]提出一种新的非平衡交通流模型,克服了高阶连续模型车辆倒退问题。Aw等[15]根据交通流各向异性的特点,用速度梯度代替加速度方程中的密度梯度得到首个各向异性的高阶动力学模型,解决了交通流的流体力学模型存在“类气体行为”和车辆倒退问题。Tang等[16]通过考虑交通流异质性扩展了速度梯度模型,该模型具有描述真实交通场景动态特性的能力。Kotsialos等[17]提出的多级宏观交通流模型,提供了更多拥塞形成机制、冲击波等其他交通流现象。针对“类气体”Prigogine等[18-19]提出基于交通流气体动力学的理论模型。Helbing等[20-21]从一个类似于气体动力学的玻尔兹曼方程系统推导出宏观多线性模型,描述包括加速、减速、速度波动等交通流状态。Hoogendoorn等[22]应用气体动力学方程提出了高阶宏观交通流模型,其能够描述多车种的相空间密度以及车辆交互时的减速行为等。Ngoduy[23]将气体动力学理论拓展到混有网联车的异质交通流,构建了宏观模型。Delis等[24]在气体动力学模型基础上,提出适应多车道的二阶宏观模型。Jin[25]通过模型归纳提出了交通流宏观与微观模型之间转变的方法。以上学者从描述交通流特性方面研究宏观与微观交通流之间的关系。
随着车辆智能化、网联化以及智能交通系统的不断完善,特别是无线通信、传感探测等进行车路信息获取技术的发展,Zhang等[26]使用光谱分析法、ARIMA和广义自回归条件异方差模型,分析了交通流的趋势、确定以及波动。为了更好地捕捉交通流的时空特性,Ma等[27]使用卷积神经网络捕捉交通流数据的空间规律。邴其春等[28]通过地点交通参数与交通状态之间的映射关系分析道路交通状态。姜桂艳等[29]将占有率、速度、流量3个交通流基础参数进行组合得到了新的特征变量。以上学者以车路信息为支撑探索参数之间的相关关系,但理论支撑较为薄弱。
上述研究在传统环境下交通流研究方法是运用数理统计和微积分等传统数学和物理方式对交通流定性定量描述,现代研究方法不拘泥于固定的公式形式发掘其相关关系,为交通工程基础理论研究与应用奠定了基础,同时可以看出,对交通流状态的描述更加偏向于交通流的运动学特性。车路协同环境下,车辆间信息交互性强、协同性好,车辆运行独立性减弱,实时精细化的车辆运动状态与交通流态势之间的协同控制(简称车/流协同控制)将成为主导。为了适应未来交通变化趋势,本文在上述研究的基础上,提出基于车辆质点系的交通流参数描述方法,既有理论支撑,又以车路信息为基础,加入动力学特性力图从新的角度诠释交通流参数的表达形式,为未来车辆节能运行工况与交通流状态的协同控制提供技术途径和方法参考。
1 交通流中车辆质点化及质点系参数
1.1 车辆质点化及其质点系
根据质点系的概念将交通流中的车辆视为质点,并以质点系参数描述交通流状态,这是基于无线通信、传感探测等车辆运行工况信息获取技术的广泛应用,以个体车辆运行工况、车辆性能参数等信息全面、快速、动态、高效的获取为前提,从车辆质点系的角度量化描述交通流状态,并分析车辆运行工况与交通流状态相互作用关系及影响机理。
在某段长为L、宽为W的单车道平直路段上,将某时刻存在于该路段上的所有车辆转化为质点,如图1所示。

图1 单车道车辆质点化及其质点系结构示意图
1.2 质点系参数表达式
单车道上车辆质点化后,在长度为L的路段范围内为一维质点系。其质点数或构成的车辆数ne随时间变化,且具有随机性。以路段起点为坐标原点,车辆行驶方向为X轴正向,建立质点系一维坐标系。记t时刻行驶于最前方车辆的编号为1,其位置坐标为x1;其后方跟随车辆编号为2,位置坐标为x2;以此类推,第i辆车的位置坐标即为xi,第n辆车的位置坐标为xn,如图2所示。

图2 设定长度范围内一维质点系的交通流 表征示意图
在图2的一维质点系中,根据质心参数公式计算质量mc、质心位置xc、质心速度vc、质心加速度ac,即式(1)—式(4)。

(1)
(2)
(3)
(4)
基于车路协同系统或车/车通讯技术的相应支持,不仅可以获得每个车辆质点的技术性能参数,如车辆质量、车身长度、发动机额定功率、额定转矩,还可以获得车辆位置、运行工况等动态信息,即车辆位置xi、速度vi、加速度ai等。在车辆质点系构成的交通流中,某时刻i车辆的质量、位置及运动状态表示为Pi(mi,xi,vi,ai)。
2 基于车辆质点系的交通流参数表达
2.1 交通量
流体模拟理论中,交通量Q即单位时间通过道路某断面的车辆数[1],即式(5)。
(5)
式中:N为车辆数;t为测量时间间隔。
基于质点系参数描述时,将交通量表征为单位时间通过道路断面的质量,即式(6)。
(6)
(7)
式中:Qc为基于质点系质量参数表征的交通量;tcL为以该时刻质心速度通过长为L的路段所需时间。
将式(7)代入式(6),整理得:
(8)
根据式(8)可得基于质点系质量表征的交通量还等于该时刻t质点系分布于单位长度上的动量,赋予了交通量相应动力学特性。
比较式(5)、式(8)得,若以当量换算法中车型的质量为基准,基于质点系质量表征的交通量可以转化为以车辆数为基础的流量,即Qc可以转化为与Q相同的量纲,即式(9)。
(9)
式中,ms为当量换算方法中基准车型的质量。
2.2 速度
流体模拟理论采用区间平均速度表示交通流的速度特性。区间平均速度是用所研究公路或道路的路段长度除以车辆通过该路段的平均行程时间[1],即:
(10)
式中:ti为第i辆车通过该路段的行程时间;n为被测车辆的个数。
基于质点系参数描述时,采用质心速度表征交通流速度,即式(3)。
任意时刻t,测量路段L内的交通流状态都在更新,如图3所示。为说明车辆质点系的质心速度vc(t)的实时计算方法,结合图3说明如下:
在图3中,第1行表示第1辆被测车辆(箭头标识)驶入测量路段L时刻的交通流构成以及状态,即观测开始时刻t1s,此时质心速度为vc(t1s);第3行表示,第1辆被测车辆驶出测量路段L的时刻t1e,质心速度为vc(t1e)。此时,图3中所示被测车辆恰好全部分布于测量路段L内。同理,记第i辆车驶出L的时刻为tie,质心速度为vc(tie)。

图3 质心速度与区间平均速度计算交通流速度状态示意图

(11)
式中:vi(t)为第i辆车在t时刻的瞬时速度;ne为该时刻被测路段L上的车辆数。

(12)
2.3 密度
流体模拟理论中密度是在指定时刻、已知长度为L的车道或道路上拥有的车辆数[1],即:

(13)
根据上文的分析,基于车辆质点系描述交通流时,将交通流密度表征为单位长度的质量。采用质心参数表达时,即:
(14)
同理将式(14)进行同量纲转化后得:
(15)
根据式(8)和式(14)得:
Qc=Kcvc
(16)
2.4 交通流参数表达形式分析
交通量随时间和空间变化具有时空分布特性,在表达方式上是某一时间段内的平均值。基于质点系参数表达时,该时间段以质心速度为基准,既具有时空分布特性,又基于规定路段所有单个车辆的个体特性,使个体特性融合性增强。
交通流速度特性的表达方式是一个将若干个个体车辆区间运行特性进行整合来刻画车辆集体的综合平均行为,但是目前,车路协同环境建设进一步发展,车辆间信息交互性强,传统交通系统中人为因素弱化,车路耦合性增强,交通流速度特性需要更加实时精确且个体车辆与交通流总体之间相互作用明确,才能适应车/流协同控制技术发展的需要。质心速度具有实时性的同时,不仅能反映质点系统整体的运动特征参数中涉及各个车的质量,对于交通流动力学特性研究引入动量、动能及其他能量状态等的描述提供基础。
交通流密度随观测时间或区间长度而变化,密度相同时交通流状态不一定相同,但采用质心参数表达时,当密度相同时可以通过质心位置参数确定车辆在道路分布的疏密程度。
综上所述,2种交通流参数描述方式的参数定义和特点,如表1所示。

表1 2种交通流参数描述方式
3 基于车辆质点系参数表达的交通流状态仿真分析
3.1 仿真分析方法及参数设置
根据2.2节提出的基于质点系参数的交通流参数表达,为了明确2种表达方式的区别与联系,采用VISSIM 6.0进行交通流状态仿真。
设置道路场景为一条长1 000 m的单车道直线路段,输出数据分别为仿真秒(s)、车辆编号、速度(km/h)、加速度(m/s2)、质量(kg)等相关数据,再将所得数据导入python进行运算;同时还设置两类交通情景:第一类不设置任何交通管制设施;第二类在末断面设置周期为60 s红灯15 s与绿灯45 s的简易交通管制设施,基本参数如表2—表4所示。

表2 基础仿真参数

表3 交通流构成参数

表4 模拟交通流状态变化参数
3.2 速度的仿真分析
3.2.1场景1:平直路段不设置任何交通管制设施
在场景1下,通过仿真验证在车辆运动速度无明显波动状态下,路段交通流状态为表3、4中车辆比例与流量输入组合时,根据式(3)、(10)—(12),对比不同的交通流速度计算方式结果的差异。


交通流组合为①一、二、三时仿真结果,如图4—图6所示。

3.2.2场景2:平直路段末断面设置交通信号灯
本节场景设置与3.2.1节形成对比,分析交通流中的车辆有明显速度波动对结果产生的影响,仿真结果对比如图7—图9所示。

图4 交通流状态为组合①一(流量逐渐增加)时的路段内质心速度与区间速度的变化

图5 交通流状态为组合①二(流量逐渐降低)时的路段内质心速度与区间速度的变化
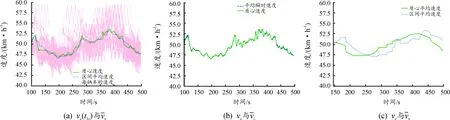
图6 交通流状态为组合①三(流量突变)时的路段内质心速度与区间速度的变化
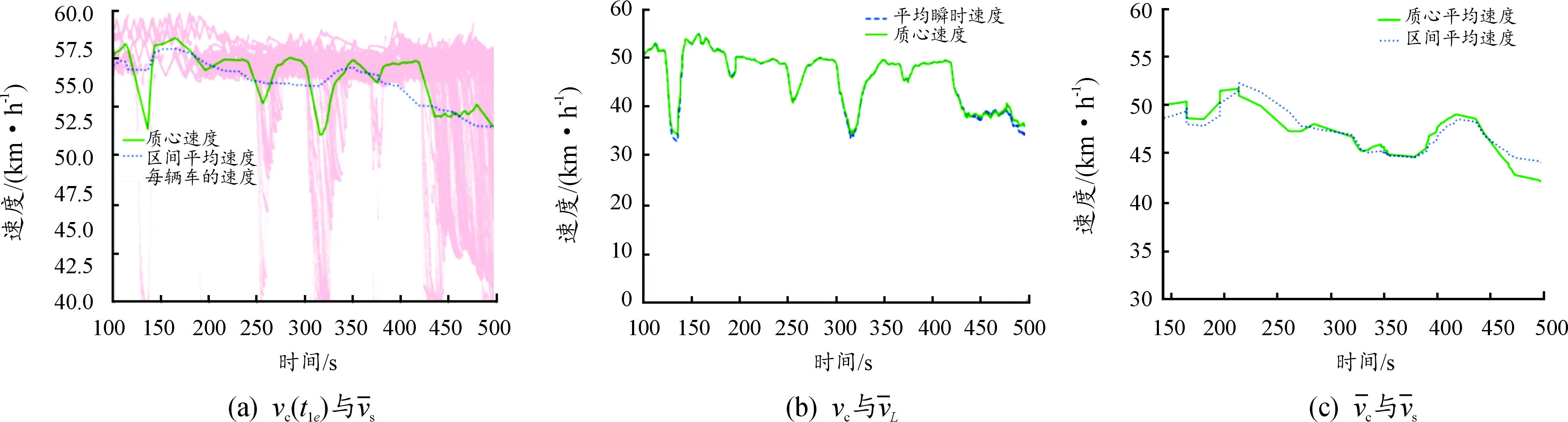
图7 交通流状态为组合①一(流量逐渐增加)时的路段内质心速度与区间速度的变化

图8 交通流状态为组合①二(流量逐渐降低)时的路段内质心速度与区间速度的变化
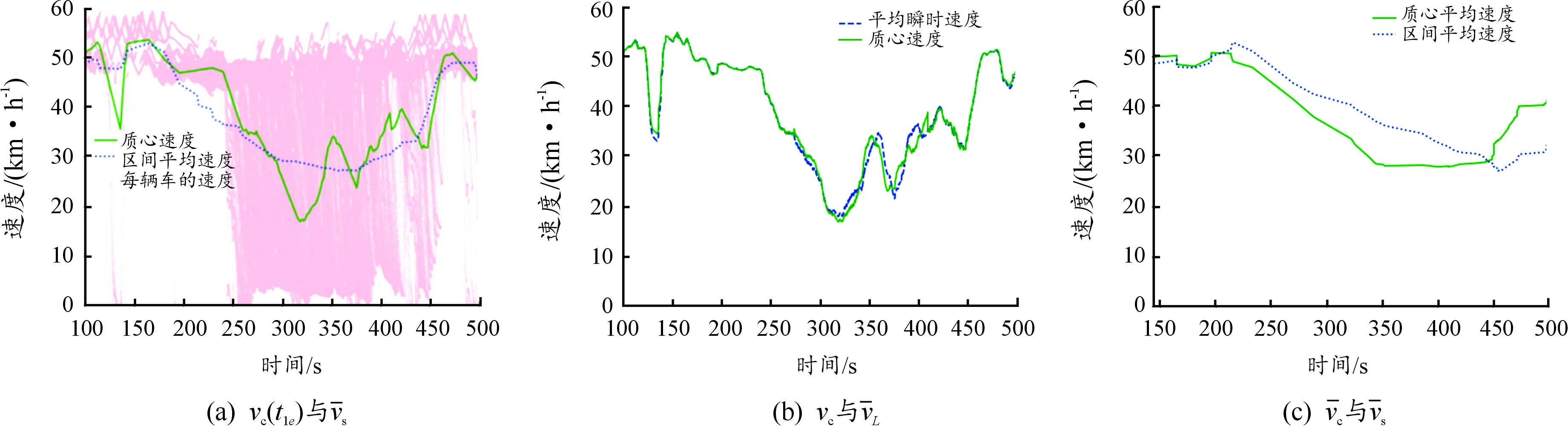
图9 交通流状态为组合①三(流量突变)时的路段内质心速度与区间速度的变化
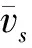
3.2.3速度仿真结果综合对比

(17)
式中,Nn为2个对比速度差值的个数。


表5 不同速度计算方式的平均差值
3.3 流量与密度的仿真分析


(18)
由于设置信号灯导致流量突变,故流量对比不涉及场景二;根据式(14)、(16)可以看出,2种密度为瞬时值,故将量纲统一后直接将仿真结果作图,如图10—图12所示。

图10 交通流状态为组合①一(流量逐渐增加)时的路段内流量与密度的变化趋势对比

图11 交通流状态为组合①二(流量逐渐降低)时的路段内流量与密度的变化趋势对比

图12 交通流状态为组合①三(流量突变)时的路段内流量与密度的变化趋势对比
4 结论
1)基于质点系方法,以路段车辆质点系的相关参数表达该路段的交通流参数,具有实时性,并将交通流中每辆车的实时微观运动状态参数直接与交通流的宏观特征参数相联系。


通过将设定长度范围内车辆质点化得到车辆质点系统,下一步将考虑引入交通流新的量化参数,表征交通流的动力学特征,如质点系动量、动能及其他能量状态等,为车辆节能运行工况与交通流状态的协同控制提供理论基础。

