基于Matlab/Simulink 软件在车门限位器主臂曲线上的分析研究

蒋东强，姜帆，李随江，杨建超

（陕西汽车控股集团有限公司，陕西 西安 710200）

引言

车门的限位器设计包括了限位器的主臂曲线设计，其设计方法多采用分段画圆-单元逼近法，设计准确性与分段数直接相关（分段数越多越准确），设计人员手工绘制过程较为繁琐也容易出错。本文对单元逼近法做以了简要介绍，并由此对限位器的主臂曲线进行了分析研究，推导出了数学方程式，并借助Matlab/Simulink 软件编写了计算程序，建立了曲线求解框图模型，通过信源控制得出了不同形状的主臂曲线，为此类设计工作提供参考依据和方法。

1 单元逼近法

单元逼近法是目前限位器主臂曲线设计时最常用的设计方法。下面以某卡车车门开启角度85°平均分为10 段为例，简要介绍图1 所示单元逼近法求取限位器主臂曲线的过程。

图1 所示限位器主臂曲线绘制过程图。（1）将DE、CF绕A 点旋转10 等份（每一等份旋转角度为8.5°），可以得到D1E1、D2E2…D10E10 和C1F1、C2F2…C10F10。（2）以B 点为圆心，分别以BC、BC1、BC2…BC10 为半径画圆，圆分别与C1F1、C2F2…C10F10 交于点G1、G2…G10，擦除多余线段G1F1、G2F2…G10F10。（3）将C10G10 绕B 点反向旋转，G10 与C9 重合，依次类推得到折线CC10，此间C10 在反向旋转过程中须始终落在最外圆边界上。折线CC10光滑处理后就得到了限位器主臂曲线，当然还应加上BC 段。

图1 单元逼近法

2 方程式推导

图2 分析图

（x1,y1）——限位器盒中心C 点的运动轨迹点 （x,y）——初始位置的限位器主臂曲线上的点 a、b、c——△ABC的边长 E——限位器主臂曲线绕B 点的旋转角度。

通过观察分析图2 我们看到C 点的运动轨迹点，即（x1,y1）都落在了以A 点为圆心b 为半径的圆弧上，且与B点坐标(BX,BY)的距离为a；( x1,y1)点可以从( x,y)以B 点为中心a 为半径旋转E 度角得到。我们可以推导如下方程式：

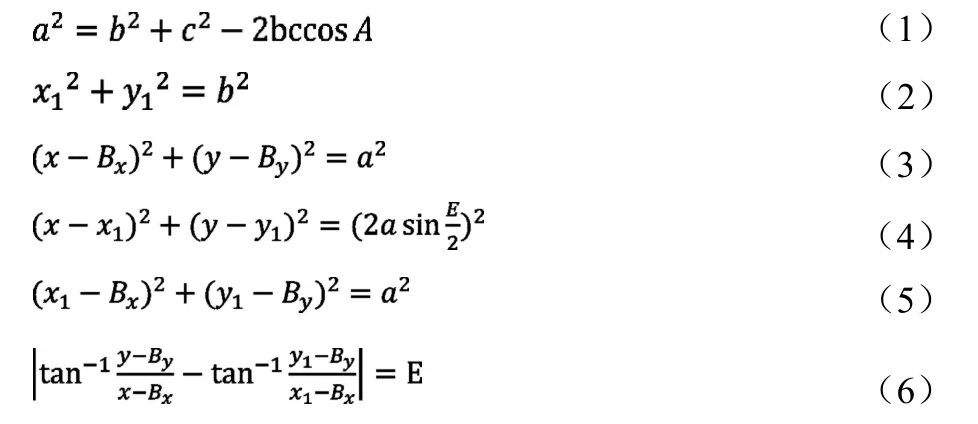
通过方程式（1）、（2）、（3）我们可以得到（x1,y1）；（4）、（5）、（6）是限位器主臂曲线（x,y）的必要条件方程。

3 Matlab/Simulink 的编程求解

虽然（4）、（5）、（6）仅是限位器主臂曲线（x,y）的必要条件方程，满足这些方程的曲线有很多，但当我们对角度E 作为单独条件接信号输入，其主臂曲线就只有一条，且主臂曲线形状可由输入信号的改变而变化。输入的信号可以是斜坡信号、正弦信号等，通过改变信号的幅值、频率、比例等参数，可改变主臂曲线线条形状，以避开车门内、外板、玻璃升降器等所占空间，最后确定的主臂曲线应在门闭合时C 点y 轴坐标以上的二维坐标区域中，且当主臂曲线以B 点旋转终了时，即当车门打开到最大角度状态下，主臂曲线不能在旋转过程中扫过铰链旋转中心点A，应保持有一定的距离。

3.1 Simulink 建模

根据方程式(1)、(2)、(3) 、（4）、（5）在Simulink 中建立图3 框图模型。我们以某卡车车门设计参数作为输入：b=83.2；Bx=60；By=39；A=21.9；运行模型。仿真时间应根据车门开启角度确定（一般卡车车门最大开启角度在85°～88°），即AC 初始位置与最终位置的夹角。这里仿真时间定为1.53s，最大步长0.01。

图3 框图模型

3.2 Matlab 中的曲线图表

在command window 窗口输入以下命令，得到限位器盒中心点(x1,y1)曲线图见图4。

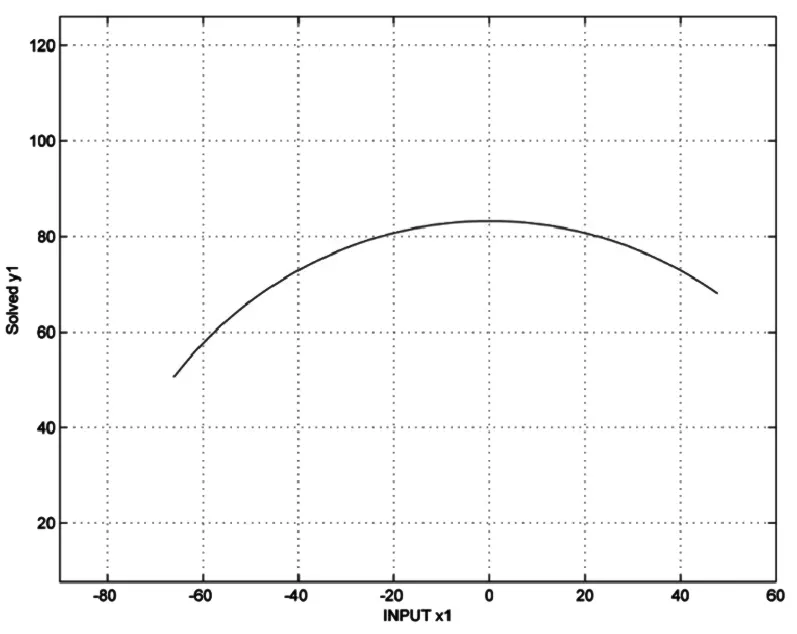
图4 x1～y1曲线图

plot(simout(：,5),simout(：,6))

axis([-90 60 40 90])

axis equal

xlabel('INPUT x1')

ylabel('Solved y1')

grid on

在command window 窗口输入以下命令，得到E 角度以正弦信号作为输入的限位器主臂曲线图5。

plot(simout(：,7),simout(：,8))

axis([-40 70 40 180])

axis equal

xlabel('INPUT x')

ylabel('Solved y')

grid on

图5 x～y 正弦信号主臂曲线图

表1 参数值

通过查看矩阵simout 的参数值表1，我们看到限位器主臂曲线（x,y）是从x 轴47.812 开始到1.5019 结束，结束点过于接近A 点的y 轴，即限位器主臂曲线在车门闭合状态下的位置可能会碰到门外板，而这正是我们设计时应避免的情况。我们将E 角的正弦信号的幅值由1 调整到1.2，将频率由1 调整到0.9，再次运行程序得到调整后的限位器主臂曲线图6。

图6 x～y 正弦信号主臂曲线图

通过矩阵simout 参数值表2，我们看到限位器主臂曲线（x,y）是从x 轴47.812 开始到22.352 结束,结束点远离了A点的y 轴。同样，我们根据车门内板、玻璃升降器等在车门内占据的位置调整E 角度正弦信号参数，进而调整曲线形状避免干涉。

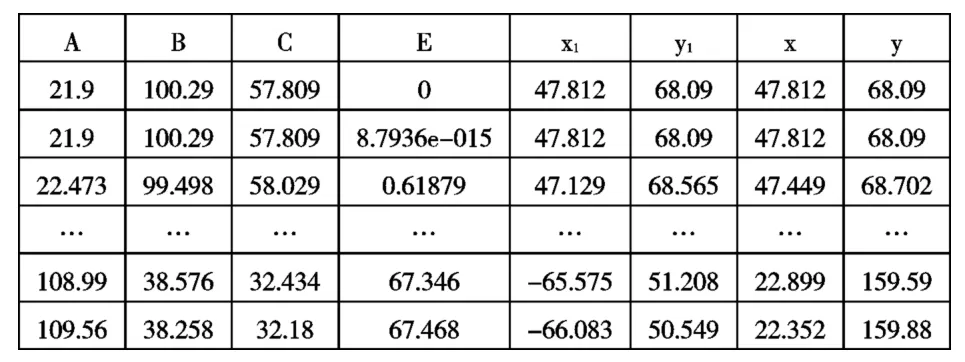
表2 参数值

3.3 更改E 角度信号源类型

我们更改图3 框图模型的E 角度信号源类型，将正弦信号更改为斜坡信号，建立新的框图程序，如图7。

图7 框图模型

在command window 窗口输入以下命令，得到E 角度以斜坡信号作为输入的限位器主臂曲线图8。

plot(simout(：,7),simout(：,8))

axis([-40 70 40 180])

axis equal

xlabel('INPUT x')

ylabel('Solved y')

grid on

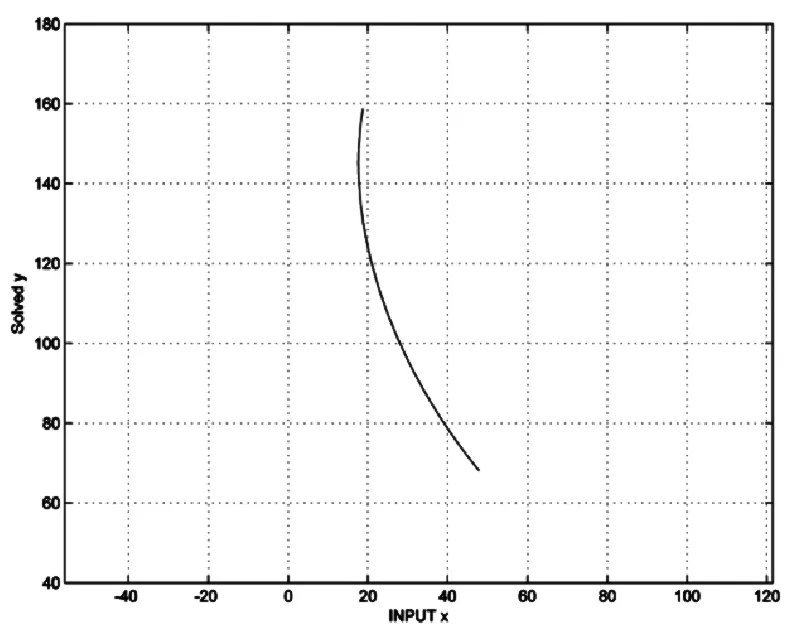
图8 x～y 斜坡信号主臂曲线图

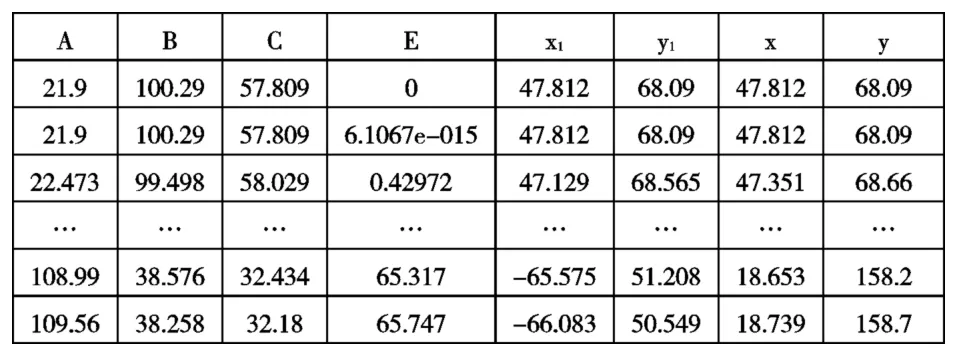
表3 参数值

通过查看矩阵simout 参数值表3，我们看到限位器主臂曲线（x,y）是从x 轴47.812 开始到18.739 结束。同样，调整斜坡信号的比例值也可以得到不同形状的限位器主臂曲线。

4 结论

应用数学软件Matlab/Simulink 编写的限位器主臂曲线程序，当知道车门旋转铰链中心点A，限位器旋转中心点B，以及限位器盒中心点C，三点布置位置和设计要求车门最大开启角度的情况下，可以快速准确地求解出车门限位器主臂曲线，并通过改变主臂曲线绕B 点旋转角度E 的输入信号参数，可调整主臂曲线的形状，避开车门内部玻璃升降器、车门内、外板等零件，以达到最终确定下一条满足设计意图的限位器主臂曲线。本文给予了这类设计问题建立了数学模型，借助计算机高效的运算效率提高了此类设计工作的效率。