基于三维至一维联合仿真的增程器废气温差发电机结构优化
王嘉伟 蓝松
(合肥工业大学,合肥 230009)
1 前言
在我国,约有24%的化石能源消耗在汽车日常行驶过程中,由于内燃机能量转换效率的限制,约有40%的能量由汽车尾气耗散在空气中[1],将这部分能量加以回收利用具有重要价值[2]。温差发电机因其结构紧凑、工作无噪声、无运动部件的特点成为汽车废气能量回收的理想部件[3]。
常见的温差发电机主要由热交换器、热电模块、冷却装置组成。废气携带的热量经热交换器传导给热电模块,一部分由热电模块转化为电能,另一部分由冷却装置带离。因此,在相同的热电模块与冷却装置条件下,由热交换器捕获的热量越多,热电模块转化的电能就越多。优化换热器的结构,使其能够捕获更多热量,可以有效提升热电发电机的输出功率[4]。在近期的研究中,优化温差发电机性能的有效方法是对其不同的组件分别建立三维与一维模型。Tae Young Kim 等[5]建立三维模型就热交换器翅片数量、高度、翅片间距及厚度对热电模块热端温度的影响进行了研究,确定了特定流场条件下的最佳翅片参数。André Marvão 等[6]为将温差发电机应用在重型载货汽车上,建立三维模型探究了影响优化温差发电机的主要因素,分别是翅片的高度、长度和翅片间距。文献[7]也建立了热电模块的一维传热模型并用于预测模块的输出电压,预测结果与试验结果具有较高的一致性。上述研究中,利用一维模型仅对特定温度下的输出电压进行了仿真,采用三维模型也仅对热电模块的热端温度进行了仿真,而使用三维模型直接对温差发电机的输出功率进行仿真几乎未进行过[8]。
本文针对增程器用废气温差发电机展开研究。普通燃油车发动机的工作点多且分散,因此,温差发电机的结构优化效果往往只能在特定工作点下才能得到最大体现。而增程发动机往往只在特定工作点下运行,为温差发电机的结构优化提供了重要的约束条件[9]。本文针对不同的热交换器建立三维流场与换热模型,对热电模块建立一维传热模型,并将2种模型进行耦合,以实现在模拟真实物理场景时对温差发电机的输出功率进行仿真。
2 模型建立
2.1 一维热电模块传热模型建立
热电模块的基本结构如图1所示,由冷、热端陶瓷板与热电结3个部分组成,故热电模块的整体传热模型可以分为2个部分,即冷、热端模型和热电结模型。
模型建立时,在热效应方面作如下考虑:
a.汤姆森热效应对传热影响小,故将其忽略;
b. 考虑热电结在有电流流经时产生的帕尔贴热效应;
c. 考虑热电结在有电流流经时产生的焦耳热效应;
d.考虑由冷、热端温差产生的塞贝克效应。
2.1.1 热电模块模型
热电结的传热热阻模型如图2 所示,其主要热阻由P-N 结热阻Ktc与之间夹杂的空气热阻Kgap构成。

图2 传热原理示意
P-N结热阻Ktc的计算公式为:
式中,n为热电模块中P-N 结的数量;ltc为P-N 结的长度;kP、kN分别为P结、N结传热系数。
热电结整体热阻Ktm的计算公式为:
式中,f为热电模块中P-N结的面积占比。
2.1.2 热效应
塞贝克效应是热电模块产生输出电压的主要热效应,而输出电压U主要与模块的塞贝克系数ΔS及冷、热端温度Tcp,c、Tcp,h相关,其计算式为:
温差发电机的电路连接见图1,回路中的主要电阻分别为P-N 结的内阻Rint与外接负载Rload,为使温差发电机的输出功率最大,将外接负载Rload与内阻Rint数值设为一致。
当回路中有电流流过时,P-N 结焦耳热效应的计算公式为:
式中,QJ为焦耳热;I为回路中的电流。
热电模块的结构较为对称,故可认为产生的焦耳热均匀地传向冷、热两端。当回路中有电流流过时,P-N 结分别向冷、热端吸、放热,即帕尔贴热效应,其计算公式为:
式中,QPc为P-N 结冷端放热量;QPh为P-N 结热端吸热量;Ttc,c、Ttc,h分别为P-N结冷、热端温度。
2.1.3 热电模块热平衡方程
根据图2 所示的传热原理,通过冷端的传热量Qcm为:
式中,A为热电模块的面积;Kcm为陶瓷板热阻。
通过热电结区域的传热量Qtm为:
热端的传热量Qhm为:
考虑前述的热效应,通过冷、热端的传热量Qcm与Qhm还有如下表达式:
2.2 三维温差发电机流场及传热模型建立
温差发电机的基本结构与尺寸如图3 所示,其热电模块被热交换器、冷却装置夹紧而形成对称的“三明治”结构。其基本尺寸为200 mm×300 mm×88 mm,上、下共布置了16片热电模块。热交换器的材质为铝合金,其导热系数为193 W/(m·K),在增程器转速为3000 r/min 的条件下,废气温度与流量分别为523 K、0.02 kg/s,冷却装置内采用温度为323 K 的冷却水进行冷却。

图3 温差发电机结构及尺寸示意
2.2.1 三维温差发电机的计算模型
由于温差发电机具有高度对称的结构,在对其进行流场、传热分析时,可选取其1/4 部分建立计算模型以节约计算时间。整个三维计算模型在STARCCM+中搭建完成,简化后的计算模型如图4所示。

图4 三维简化计算模型示意
2.2.2 三维模型的边界条件设定
三维模型整体分为耦合区域与非耦合区域,耦合区域(热电模块区域)由STAR-CCM+与AMESim共同计算完成[10],非耦合区域由STAR-CCM+独立计算完成。
入口设为质量流量入口,出口设为压力出口,设置3个对称面,见图4。由于冷却水拥有相对较大的热容,而通过冷端流向冷却装置的热量较少,将冷却装置设为固定温度。
2.3 三维模型与一维模型的耦合
耦合区域的结构如图5 所示,取各表面的平均温度作为计算温度。在每一次迭代中:由STARCCM+分别计算出冷端温度Tcp,c、热端温度Tcp,h、热电结冷端温度Ttc,c、热电结热端温度Ttc,h后传输至AMESim 端进行冷端接触热阻Kct.c、热端接触热阻Kct.h、热电结热阻Ktm、冷端帕尔贴吸热量QPc、热端帕尔贴放热量QPh、焦耳热QJ的计算后,将数值回传至STAR-CCM+端进行下一次迭代计算。上述耦合原理如图6所示。

图5 耦合区结构示意

图6 耦合原理示意
2.3.1 三维模型的耦合区边界条件设定
热电模块的冷、热端均与其他壁面直接接触,由于不完全接触产生的基础热阻Kct.c、Kct.h的数值设置为由AMESim 端输出的计算结果,冷、热端的陶瓷板导热系数λ设置为35 W/(m·K),因为焦耳热效应与帕尔贴热效应的发生,热电模块的热端陶瓷板与热电结的接触面设为热通量的流入,根据式(10)可得热通量为-QPh-0.5QJ,同理,根据式(11),热电模块的冷端陶瓷板与热电结的接触面的热通量为-QPc+0.5QJ。
2.3.2 热电模块的接线方式及输出功率的计算
计算模型的热电模块每4 块串联为一组,则其输出电压Uout为各模块的输出电压之和:
内阻Rint为各模块的内阻之和:
式中,U1~U4为模块1~模块4的输出电压;Rint1~Rint4为模块1~模块4的内阻。
将外部负载Rload设为与内阻Rint数值相等,则输出功率Pout为:
将温差发电机接入汽车的排气系统势必会引起发动机的排气背压升高,进而降低发动机的输出功率[11],发动机转速3000 r/min 工况下的损失功率为:
式中,ΔP为温差发电机的压力降。
此时温差发电机的整体净输出功率Pnet应弥补这部分功率损失:
2.3.3 网格测试
在完成上述全部模型搭建后,对STAR-CCM+中的三维模型进行网格测试,在模型相同的条件下,通过不断减小网格的尺寸来提高网格的总数量。当网格尺寸减小至0.01 m、整体网格单元数达到400000 个时,所需要的所有计算数值及温差发电机的进出口压力降ΔP的变化均小于0.5%,采用此时的网格尺寸和数量进行计算。
3 温差发电机的结构优化
在4 片热电模块上方的热交换器处增加4 组翅片结构作为对照组,翅片的基本尺寸为60 mm×2 mm×7 mm,每组设置5 个翅片,翅片间的中心距离设为10 mm,将第4 片热电模块区域内的翅片与其他区域的翅片错开得到改进结构1,将改进结构1 中第4片热电模块周围的翅片各向左、右倾斜10°得到改进结构2,将所有翅片结构更改为与改进结构2 第4片热电模块周围相同的结构得到改进结构3。4 种结构如图7所示。

图7 各结构示意
为探究翅片参数对温差发电机的性能影响,继续在改进结构3的基础上对翅片不同的张角与间距进行仿真。
3.1 气流速度分布
4 种结构的气流速度分布如图8 所示:由于第4 片热电模块周围翅片结构的变化,其翅片周围的气流流速随着扰动的变大而提高,由于热交换器整体结构的变化,热交换器内的整体平均流速也随着扰动的增大而提高,4 种结构的湍流强度均逐渐增强。

图8 各结构的流速分布
3.2 温度分布
湍流强度增强会使边界层变薄,边界层热阻随之减小,对流传热得到了强化。传热逐渐强化的4种结构温度分布如图9所示:随着传热的不断强化,4种结构的平均温度逐渐提升,因为第4片热电模块周围翅片的结构与位置的变化,产生的扰动使其热端温度得到提升。

图9 各结构的温度分布
3.3 输出功率及压力降
各结构热电模块的输出功率如图10所示:随着热交换器的温度升高,各模块的输出功率提高。表1 所示为各结构的压力降、功率损失及总的净输出功率。由表1 可以看出,热交换器的结构变化带来扰动的增加,发动机功率损失随压力降的增加而增大。改进结构3 的发动机功率损失最大,约为基本对照组的2.5 倍。但是,通过进一步比较总的净输出功率可以发现,扰动增加所带来的温差发电机功率的提升效果比压力降造成的功率损失效果更为明显。改进后温差发电机的总净输出功率与基本对照组相比,分别提升了6%、3%、8%。
3.4 翅片参数对发电机性能的影响
将左、右两侧翅片张角设定在0°~15°范围内变化,得到净输出功率如图11 所示。综合考虑前述“扰动”及“压力降”的因素作用,8°为翅片的最佳性能张角。

图11 不同翅片张角的净功率输出
保持最佳张角8°不变,在空间允许的条件下改变翅片的间距,使其在7~10 mm 范围内变化,最大净输出功率计算结果如图12 所示。由图12 可知:随着翅片间距的增大,最大净输出功率也一并增加,10 mm是在空间允许条件下的最佳翅片间距。
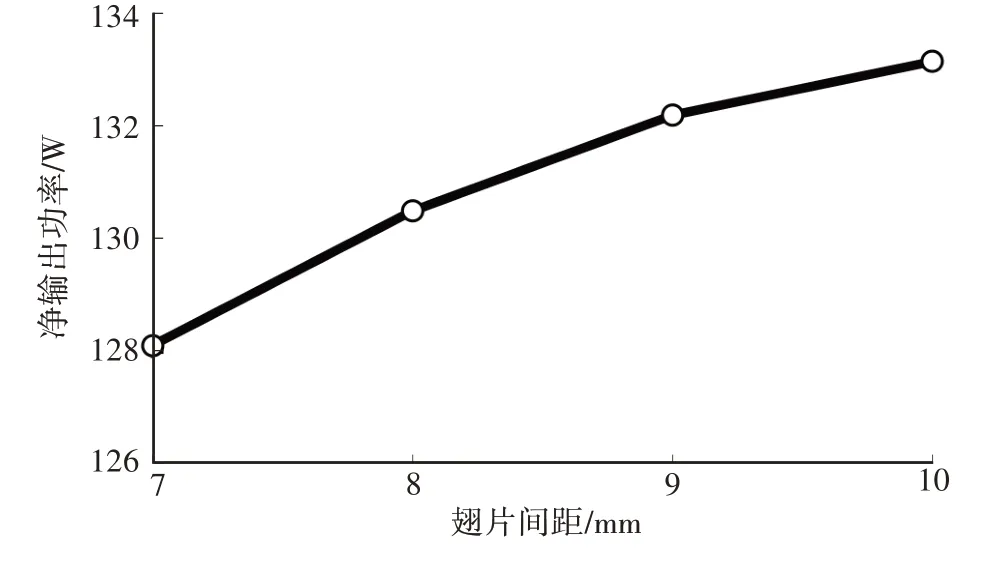
图12 不同翅片间距的输出功率
4 结束语
本文使用三维至一维联合仿真的方式对温差发电机的性能进行了探索。分别对热电模块和温差发电机建立一维传热模型和三维模型,并对2 种模型进行了耦合,耦合模型有效解决了传统模型只能单一分析温差发电机的温度场,而不能反映温差发电机输出功率的局限性。耦合模型可以更加真实地反映实际的物理情况,通过耦合模型间实时交换的数据,可以对温差发电机的输出功率进行仿真,进而将结构优化的结果更为直观地体现在输出功率上,更有效地为温差发电机的结构优化提供参考。
本文对多种不同翅片结构的温差发电机进行了比较。换热器翅片错位且在翅片间距10 mm、张角8°条件下的净输出功率最高,为133 W,相较于翅片整齐排列且无张角的基本对照组,其输出功率提高了约14%。该计算结果表明:在相同的热电模块与冷却装置下,优化热交换器的结构可以有效提升温差发电机的输出功率,但仍需考虑结构变化带来的发动机排气背压变化导致的净输出功率变化。综合考虑翅片结构所带来的强化传热与排气背压是优化温差发电机的关键。

