基于TED原理的燃气灶发电模型及数值模拟

刘 畅，唐 豪

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

燃气灶在我国的使用范围非常广泛，主要燃料是甲烷，其燃料具有清洁、热值高等优点[1]。城市家庭、酒店以及大型食堂是使用燃气灶的主力军。然而，在实际的生产中，人类仅仅利用了一部分能量，另一大部分热量耗散在空气中，无法被合理利用。

半导体温差发电作为一种新型的发电模式，具备环保、寿命长等优点。国内外也进行了相应的研究，如日本政府开展基于温差发电的“燃料燃烧能源回收计划”[2]项目。国内李颜哲[3]等人研究核心流强化传热技术对余热转化电能的性能影响。本文提出一种针对燃烧设备的温差发电模型，在不影响燃气灶正常工作的前提下，环绕在燃气灶周围，形成一个发电圈。发电圈热端在内，接收火焰辐射的温度；冷端在外，采用水冷的方式提升两侧的温差，效果图如图1所示。

图1 带有温差发电装置的燃气灶

1 发电模型及设计意义

1.1 温差发电模型

根据塞贝克效应，将P型和N型两种热电材料连接构成一个PN热电偶，将PN热电偶置于不同温度之间，两端出现温差，如图2所示。热激发效应产生，热端与冷端的电子浓度发生变化，在浓度梯度的驱动下，空穴和电子从热源端向冷端转移，形成电动势，电路闭合即可产生电流[4]，热电材料就通过两端温差可实现热力发电。

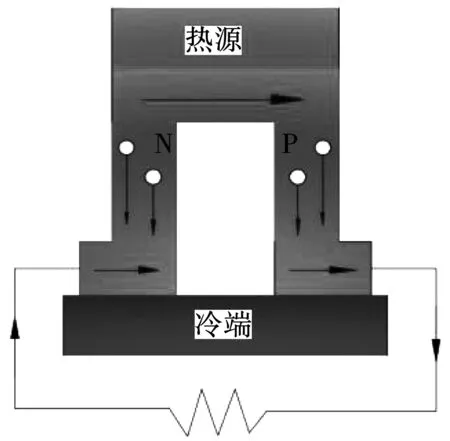
图2 温差发电示意图

两导体之间的电压计算公式为

ΔU=αΔT

(1)

α=αP-αN

(2)

式中 ΔU——温差电动势；

α——赛贝克系数；

ΔT——冷热端温差。

1.2 设计意义

该发电系统主要由冷热端、半导体发电片、稳压模块、冷却水以及蓄电池组成，通过热电效应进行电能的转化。

调查研究发现，燃气灶工作时内焰温度约为1 073～1 173 K，外焰温度约为1 673 K，在空气良好助燃时温度更高，为发电模型提供了良好的热源供应条件。

李雪晴[5]等人设计了一种燃气灶余热发电实物并进行实验。通过实验的测定，一个发电片输出功率可达2 W，若干个发电片组成的系统可产生40 W左右的功率。经过稳压模块后，可产生稳定电压，为低功率用电器供电，节能环保。特别的是，在大型、长时使用燃气灶的工作场所，该温差发电模型更具有使用价值。

2 系统模型设计的基本依据

2.1 热辐射

在自然界中，物体在发出辐射能与吸收周围物体发来的辐射能同时进行。物体辐射出的能量与吸收的能量的差值，即其输送出去的净能量。另外，温度的提升会使物体的辐射能力急速加强。

电磁波辐射可以实现冷热端能量有效地运输，属于非接触式换热，不光可以在空气中传播，也可以在真空中。在生产生活中接触到的温度范围内，只有位于0.38～1 000 μm之间波长的热辐射具有实际意义[6]。

2.2 辐射角系数

辐射换热角系数表示一个固体表面吸收另一个固体表面发射的辐射能量占辐射总量的百分比。反映了固体面位置关系对辐射换热的作用，角系数是一种几何因子，与辐射源及辐射体表面的温度及发射率无任何关系[7]。

定义不同位置微元面的辐射角系数为

(3)

式中l——微元面dA1和dA2之间的距离;

θ1,θ2——两微面元中心连线夹角与法线夹角。

3 温差发电模型建立

许艳艳[8]等人在温差发电器热端设计的过程中发现，带有栅格的平板热端，温度利用效率要比无栅格时平均提升约20%。针对燃气灶提出一种基于TED(热电装置)的温差发电模型，在满足使用要求的同时，将模型中热端加上格栅板结构，并在热端上设置对流通风口。如图3所示，发电圈高度为60 mm,热端使用钢制材料。钢制材料的吸收系数比较高，在本文仿真模拟中将其近似于黑体，吸收系数接近于1。假设燃气灶工作时火焰均匀燃烧，可以利用固体火焰模型求解。火焰辐射出的电磁波，发电圈热端的格栅中经过多次反射后，辐射出去的电磁能较少，热端接收的能量效率显著提高。设计的发电模型结构示意图如图4所示。

图3 热端设计图

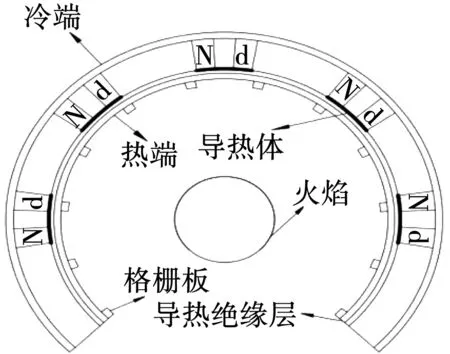
图4 发电圈结构示意图

3.1 控制方程

计算区域为半导体元件、格栅及热源与热端之间的部分。固体火焰模型假设圈内火焰是一个圆柱形、均匀辐射源，火焰的表面辐射强度为一个与波长无关的常量空气透射率是距离、环境温度与相对湿度的函数，与波长无关[9];本文主要研究发电系统内的流场、温度场的变化关系。为了简化计算，对以上模型作如下假设:

(1)火焰表面温度差异不大，即火焰表面温度相同；

(2)火焰形状为垂直的圆柱体，圆柱体底面直径为与燃气灶中心圈直径相等；

(3)流体状态处于局部热力学平衡。

对于定常流动、不可压缩流体，控制方程包括：

质量守恒方程

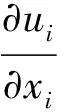
(4)

动量守恒方程

(5)

能量守恒方程

(6)

式中x——长度坐标/m；

u——速度/m·s-1；

ρ——密度/kg·m-3；

g——重力加速度/m·s-1；

p——压力/Pa；

μ——粘性系数/Pa·s；

cp——比定压热容/J·(kg·K)-1；

T——温度/K；

λ——导热系数/W·(m·K)-1；

φ——耗散函数/W·m-3。

3.2 建模及边界条件设定

由于研究模型热端表面及圈内流场，采用三维的计算模型，网格划分为非结构化网格。采用湍流k-ε标准模型。压力与速度的耦合关系采用SMPLE耦合方法。由于DO(Discrete Ordinates)模型可用于求解从离散的立体角发出的热辐射且计算精度较高，故选择DO辐射模型进行数值模拟[10]，其中添加重力因素g=9.8 m/s2。在本文的数值模拟中，热端与热源之间为半开放空间，底面与热端假设为热通量为零的固壁，其他开放空间的边界条件设为压力出口，空气吸收系数设为0.2。

4 仿真结果分析

4.1 无格栅与有格栅对比分析

假定热源区域温度固定为1 200 K，分别对模型热端在有无格栅的条件下进行数值仿真计算。此半导体发电模型半径为100 mm，其圆弧角度为270°，火焰分布近似呈圆柱，半径为50 mm，高度为50 mm。对流通气孔位于模型中间部位，其圆弧角度为36°，高度42 mm。进行热端有格栅的仿真计算时，格栅高度是4 mm。

仿真的结果如图5、图6所示，发电模型的热端在增添一定数量的栅板后，热端表面积由217 cm2增加到314 cm2,其平均温度明显提高，平均温度值由522 K提高到568 K，表面的热流密度由20 082 W/m2降低15 120 W/m2。在辐射温度云图中可以看出，除了压力出口处，有格栅热端近壁面附近比无格栅时有较少的低温区，温度相对变化较小。假定半导体发电模型冷端温度为300 K，通过计算，热端增添格栅后热端对热源释放的热能利用率提高18.47%，冷热端平均温差相对提高了20.72%。

图5 无格栅时辐射温度分布图

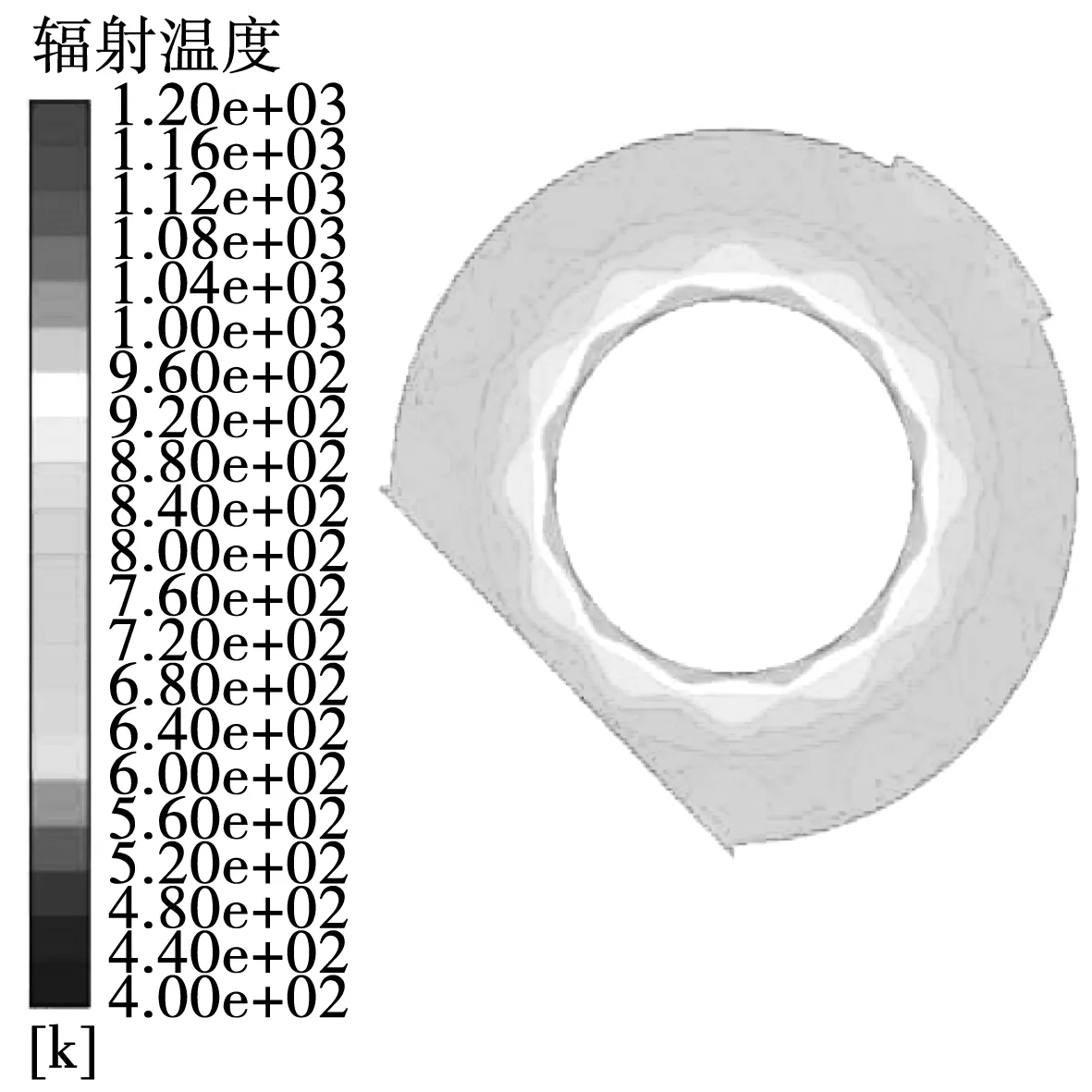
图6 有格栅时辐射温度分布图

电磁波可以输送辐射能，由热源进入到格栅后，经过多次反射，大部分电磁能被格栅及热端吸收，即热源发射出的电磁能损失很小，从而热端温度上升。因此，改进后的温差发电装置可以更好的收集到热源散发到空气中的热量，提高温差发电装置冷热端温差，提升了余热回收的效率。

4.2 格栅处于不同高度时温差发电器的热端温度

在进一步研究中，保持热端设置格栅的条件不变，给予热端与底面一个倾斜角α。α分别取60°、90°，通过对温度场分布情况对比分析，当参数收敛时，热端表面的温度会高于垂直的情况。在热端表面温度云图中，垂直时高温区集中在下半区；而在α为60°的条件下，热端温度分布均匀，且温度较高。温度分布图如图7、图8所示。

当辐射电磁能向热端传输的过程中，倾斜角α为60°时，热源辐射到热端上的能量百分比较大，加上格栅的作用，热端温度更高。空气在热源附近吸收热量，由于重力作用，在底部堆积，然后通过传热作用传递给热端，所以热端的下半区温度较高。倾斜角α为60°时，由于热端下半区距离热源较远，加上空气的传热作用，两者相互影响，整个热端区域温度差异不大。

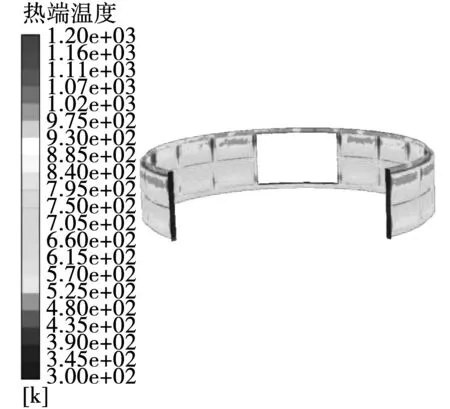
图7 倾斜角90°时热端温度分布图

图8 倾斜角60°时热端温度分布图

为了更好的研究热端倾斜角度对热端热量收集效果的影响，在保持热端高度和对流通风口大小一致的条件下，分别取倾斜角α为45°、60°、75°、115°、120°以及135°有格栅的热端进行数值仿真模拟。通过对数据的记录整理，与无格栅90°热端进行对比，得到不同倾斜角α下温差提高率、热端温度值与热流密度值等数据，分别如表1、图9及图10所示。

表1不同倾斜角温差提高率

倾斜角α/°45607590105120135效率η/[%]27.557.748.620.728.84.9-44.2

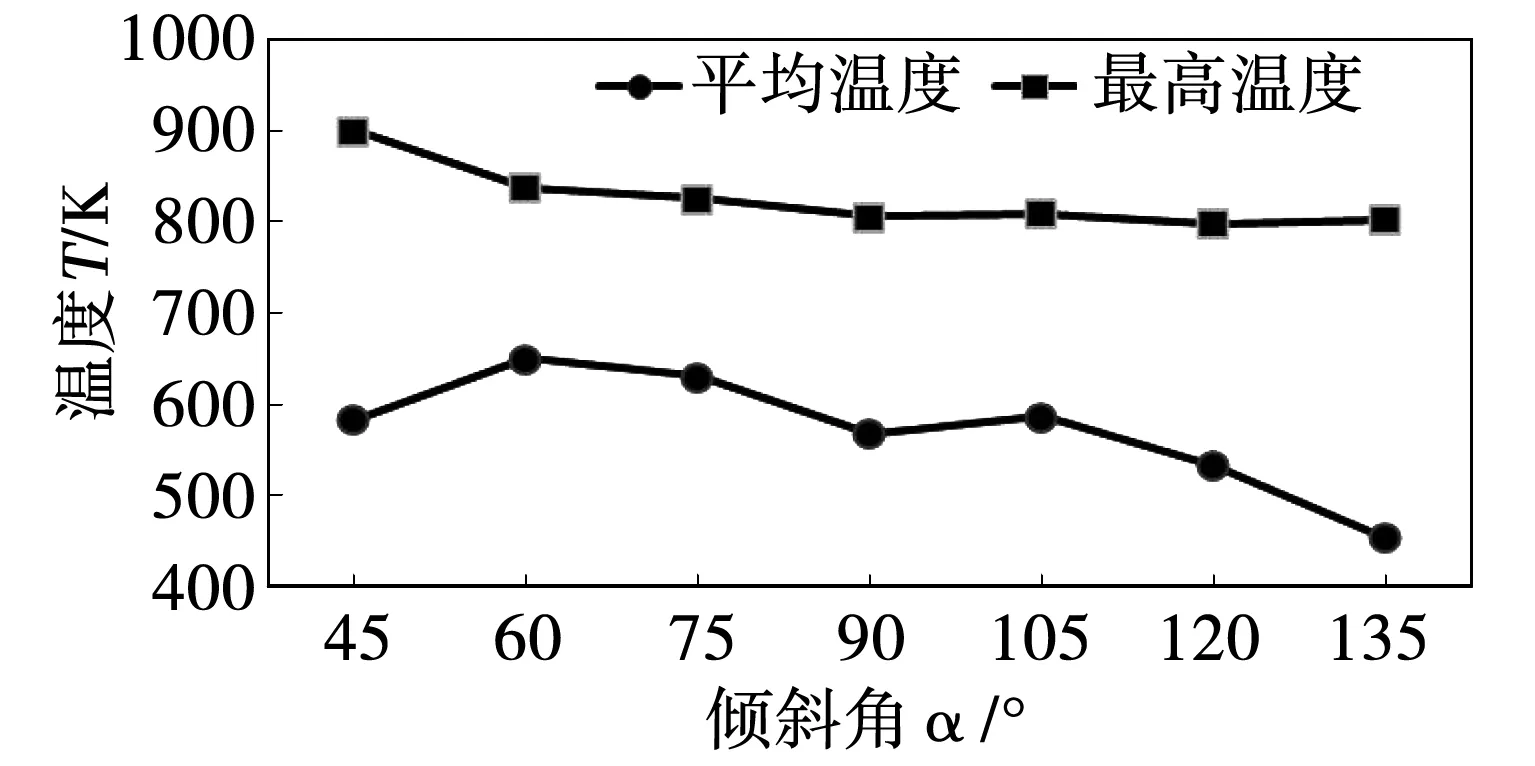
图9 不同倾斜角下热端平均温度与最高温度

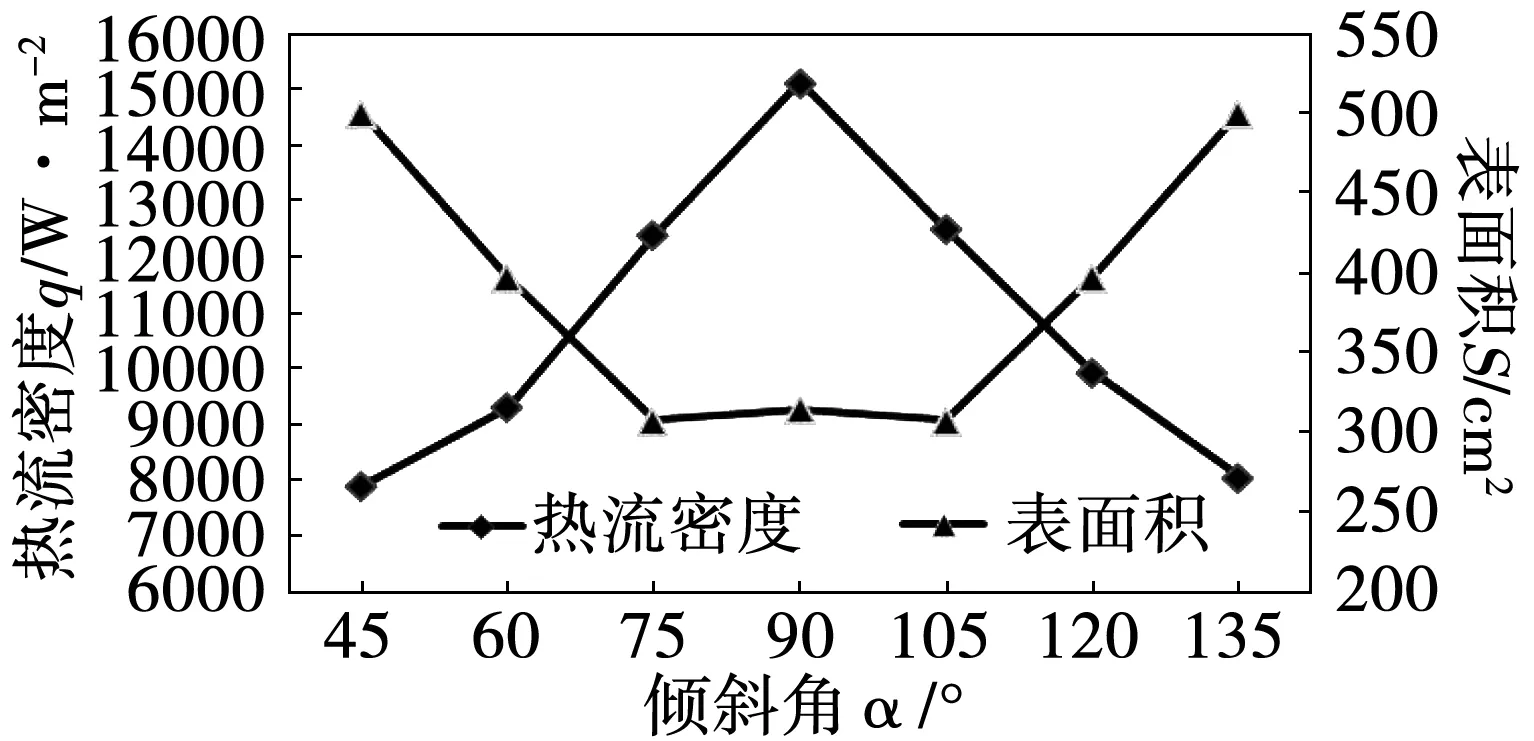
图10 不同倾斜角下热端热流密度与表面积大小

从上述图表中可以看出，倾斜角α在60°时温度与温差提高率最高，α为90°时温度表现出一个转折，成为一个低谷，经过105°之后，温度值持续下降；α为45°时热端最高温度最高，其他倾斜角下最高温度差距不大。倾斜角α在90°之前，热流密度呈现递增趋势，在90°之后呈现递减趋势，热端热流密度与表面积大小数值分布近似于y=90°对称。

5 总结与展望

本文以燃气灶设备为研究对象，提出了一种半导体温差发电模型，进行废弃热能的回收利用，探讨了燃气灶热量回收的工作模式及原理。在研究中发现，通过对发电模型热端改造设计，以及热端与底面倾斜角度的改变，得到了不同的余热回收效果。在数值仿真中，通过对模型系统内的温度场、流场分析，得到如下结论：

(1)半导体温差发电模型热端设计成带有格栅的结构，可以增加辐射电磁能在格栅内的反射次数，发电模型冷热端温差增大，温差提高约20.7%。

(2)在保持发电模型高度即热端竖直高度不变的情况下，在本文所选倾斜角度中，倾斜角α为60°左右时，热量收集效率最高。

(3)在保持热源辐射强度不变的情况下，改变热端的倾斜角，热端的平均温度和平均热流密度也随之改变。

燃气灶发电装置在使用时会受到环境温度、气流大小及火焰实际温度大小[11]等各种因素的影响，本文所做的模拟只是一个理想化结果，更准确的数据需要经过实验进一步测得。另外，针对热端结构的设计不仅仅针对于燃气灶设备，在垃圾发电厂、钢铁炼钢厂等大型燃烧设备[12]等各类生产生活中皆可运用，半导体温差发电是低品位能源利用的重要趋势。