基于支持向量机的汽轮机排汽焓计算
杨 斌,杨永军,邢乐强,兰 斌,徐世明
(1.西安热工研究院有限公司,陕西 西安 710054; 2.陕西清水川发电有限公司,陕西 榆林 719000;3.华能营口热电有限责任公司,辽宁 营口 115003)
随着发电行业步入信息化时代,需要在线计算汽轮机组的经济性,难点在于汽轮机低压缸排汽焓的在线计算[1]。低压缸排汽品位低,且是湿蒸汽[2],除了需要排汽压力和排汽温度外,还要利用湿蒸汽干度,才能计算其焓,然而,低压缸排汽干度没有在线测量装置[3],这就无法在线计算低压缸的排汽焓,进而无法在线计算低压缸效率以及汽轮机组的经济性[4]。
许多科研工作者对低压缸排汽焓的在线计算做过深入研究。任浩仁等人通过曲线外推的方法来计算汽轮机低压缸的排汽焓,该方法在低负荷以及变工况运行时并不理想,计算精度差[5]。韩中合等人通过能量平衡的方法来计算汽轮机的排汽焓,该方法计算所需数据多,且计算工作量大、计算步骤繁琐,缺乏实时性差[6]。郭江龙等人通过熵增计算的方法来计算汽轮机的排汽焓,考虑到辅助汽水的流量分布,实用性不大[7]。李慧君等人通过等效焓降的方法来计算汽轮机低压缸的排汽焓,该方法在变工况时精度也差[8]。国外工程应用中常用的Baumann法则计算汽轮机低压缸效率[9],此外Phillip J Kearney 、Mario lvarez Fernndez等从工程以及理论的角度研究了低压缸排汽焓及缸效率的计算方法[10-11]。
近年来,机器学习不断兴起,不少科研工作者利用机器算法来计算汽轮机低压缸的排汽焓,并在这方面研究中取得了一定成果。吴俊杰等人通过神经网络实现了低压缸排汽焓的计算[12]。王慧杰等人通过最小二乘支持向量机计算了低压缸排汽焓[13]。米兰等人通过支持向量机计算了低压缸排汽焓[14]。本文通过支持向量机(SVM)建模来计算汽轮机低压缸的排汽焓[15],采集更全面的历史数据并对数据进行预处理剔除换点,以保证模型训练的精度。
1 支持向量机
支持向量机专门针对有限样本的机器学习理论,比传统的基于无限样本的学习理论更符合实际情况。学习过程包含模式识别、函数逼近等[16-21]。
线性可分样本集(xi,yj),i=1,…,n,x∈Rd,y∈{+1,-1}满足分类超平面的标准约束形式,其表达式如式(1)所示,d为点x到超平面(w,b)的距离
yi[(w×xi+b)]-1≥0,i=1,…,n
(1)
(2)
(3)
式中αi——拉格朗日因子。
对(w,b)最小化L(w,b,α),可得式(4)和式(5)
(4)
(5)
从而可以进一步求得对偶优化问题,如式(6)所示,还可以得到最优分类函数f(x),如式(7)所示
(6)
f(x) =sgn{(w·x)+b}
(7)
(8)
式中x(1)——第一类的某个支持向量;
x(-1)——第二类的某个支持向量。
2 排汽焓计算的模型
汽轮机的进汽参数和抽汽参数都会影响汽轮机低压缸的排汽参数,从而进一步影响到汽轮机低压缸的排汽焓,本文选取机组负荷,主汽流量、压力和温度、调节级后压力和温度、中压缸进汽压力和温度等进汽参数作为SVM模型的输入变量,同时,选取高压缸排汽压力和温度、低压缸排汽和温度等排汽参数作为SVM模型的输入变量,此外,还选取汽轮机八级回热系统的抽汽压力和温度等抽汽参数作为SVM模型的输入变量,总计共28个参数作为SVM模型的输入变量,汽轮机排汽焓作为输出变量,建立基于支持向量机的汽轮机低压缸排汽焓计算模型。本文先对采集到的历史数据进行数据预处理剔除明显的坏点,剔除坏点后的数据用于对SVM模型进行训练和验证,其计算流程图,如图1所示。

图1 基于支持向量机模型的排汽焓计算模型图
2.1 数据预处理
机组运行过程中热工参数偶尔会受到干扰产生坏点,这些坏点偏离了真实值不能用于模型的训练,必须要将其剔除,因此训练SVM模型前先要对采集到的历史数据进行数据预处理。本文用证实法对历史数据做预处理[22],利用历史数据趋势预测紧跟着的下一个数据,再对比预测值与实测值,以验证实测值的正确性,其具有占用内存小、计算量小等特点,适合在线计算,计算模型如下
(8)
X=(x1,x2,…,xm)T
(9)
式中xm+1——预测值;
m——前m个数;
X——原始数据矩阵;
B——系数矩阵;
T——矩阵转置运算。
本文取当前采样数据之前的十个正常数据样本点作为历史数据,用五阶不加权预测模型,计算得到的预测系数矩阵为B=(0.41,0.06 ,-0.37,0.37,0.53)。当预测值和测量值之差超过20%时,就用预测值代替测量值。
2.2 归一化原理
采集到的28个输入变量和输出变量相互之间的单位并不统一,数量级也存在差异,利用归一化原理将其转换为无量纲量,以消除量纲和单位的差异对SVM模型训练的影响,模型输出预测结果时反归一化[23-25],归一化公式为
(9)
式中x——归一化前的值;
x′——归一化后的值;
ymax——归一化范围的最大值;
ymin——归一化范围的最小值。
归一化后的数据均落在-1到1之间。
3 实例计算
本文以某300 MW汽轮机组为例进行计算,该汽轮机组为亚临界、一次中间再热、双缸双排汽、单轴机组,并设置有八级回热系统,三个高压加热器、一个除氧器和四个低压加热器。该汽轮机组运行状况良好,本文采集了一段时间内该汽轮机组的全负荷工况下的运行数据,包含了前文提到的28个输入变量和1个输出变量的数据。由于采集的历史数据量较大,数据组数较多,不便于列表展示,本文仅将机组排汽焓数据进行图表展示,如图2所示。

图2 数据预处理前排汽焓分布
图2可知,原始数据排汽焓中有一些明显的坏点,不能用于模型的训练,所以需要对原始数据进行预处理。本文将排汽焓运用前文介绍的证实法进行数据预处理,处理后的数据如图3所示。

图3 数据预处理后的排汽焓分布
由图3可知,数据预处理后的排汽焓值,明显剔除了坏值点,数据更符合机组运行的实际情况。运用同样的方法,对28个输入参数,进行数据预处理,以剔除其中的坏点,方便更好的用于支持向量机模型的训练。
3.1 模型训练
本文将剔除坏点后的各个工况下的历史数据随机选取250组具有代表性的数据作为训练样本数据,50组数据作为验证样本数据,用训练样本数据来对支持向量机模型进行训练,再用验证样本数据来验证模型训练的效果,由于数据量太大,不便于全部展示,本文仅列出典型工况下的部分训练数据,如表示1所示。
表1部分训练样本数据展示
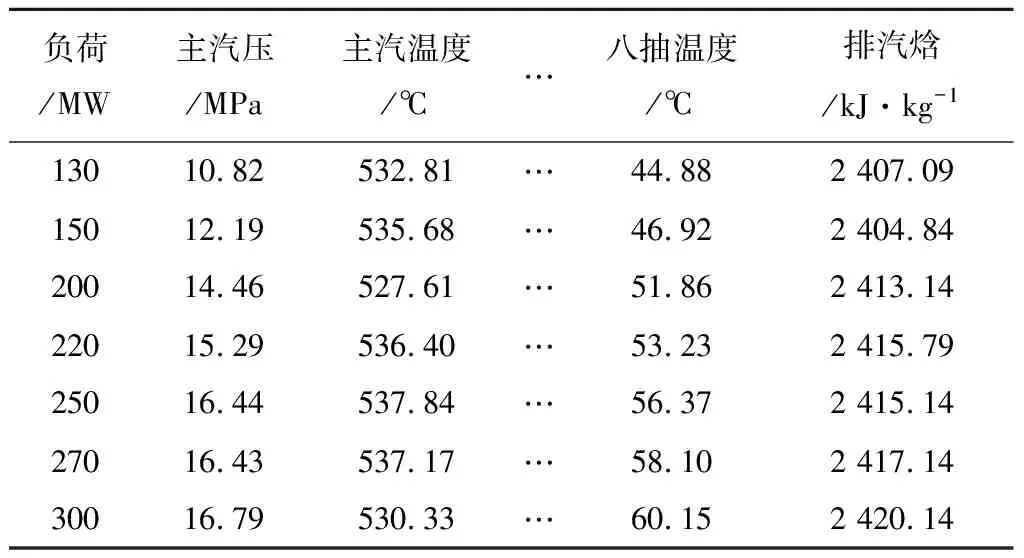
负荷/MW主汽压/MPa主汽温度/℃…八抽温度/℃排汽焓/kJ·kg-113010.82532.81…44.882 407.0915012.19535.68…46.922 404.8420014.46527.61…51.862 413.1422015.29536.40…53.232 415.7925016.44537.84…56.372 415.1427016.43537.17…58.102 417.1430016.79530.33…60.152 420.14
由于采集到的历史数据的量纲并不一致,数量级也不一致,为了消除量纲和数量级对模型训练的影响,首先对剔除坏点后的所有历史数据做归一化处理,归一化处理并不改变各个参数的变化规律。经过归一化后的数据用于SVM模型的训练,支持向量机模型的核函数选用RBF径向核函数。
3.2 模型验证
本文用验证样本数据来验证SVM的模型训练的效果,将验证样本数据带入训练好的SVM模型中,得到汽轮机排汽焓的预测值,由于数据量太大,在此仅展示典型工况下的部分预测结果,如表2所示。
表2部分验证样本数据展示
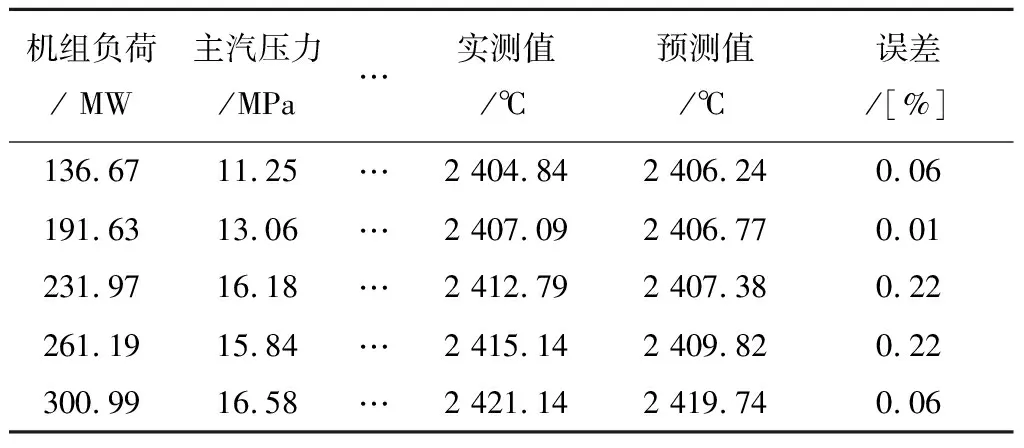
机组负荷/ MW主汽压力/MPa…实测值/℃预测值/℃误差/[%]136.6711.25…2 404.842 406.240.06191.6313.06…2 407.092 406.770.01231.9716.18…2 412.792 407.380.22261.1915.84…2 415.142 409.820.22300.9916.58…2 421.142 419.740.06
由表2可知,基于支持向量机的汽轮机排汽焓计算模型的预测精度高,无论是在低负荷、高负荷运行工况下,还是变工况下,误差都在1%以内,符合工程要求。计算精度比文献[6]中传统的能量平衡法高,绝对误差小5 kJ/kg左右,计算精度与文献[12]中神经网络法相近。本文着重分析机组负荷与排汽焓实测值、预测值之间的关系以及排汽焓的实测值与预测值之间的关系,并绘制了相应的图表。机组负荷与排汽焓实测值的关系,如图4所示。机组负荷与排汽焓预测值的关系,如图5所示。排汽焓的预测值与实测值的关系,如图6所示。

图4 机组负荷和排汽焓实测值
由图4可知,在低负荷工况时,低压缸的排汽焓的实测值波动较大。高负荷工况时,低压缸的排汽焓的实测值相对较稳定,汽轮机组由低负荷升到高负荷时,排汽焓整体上略有上升。整个负荷工况下,汽轮机低压缸的排汽焓都在2 404到2 422 kJ/kg范围内波动,且机组运行工况变化时,低压缸排汽焓略有波动。
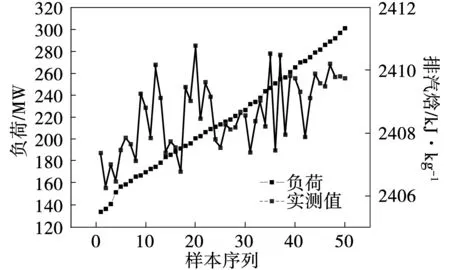
图5 机组负荷和排汽焓预测值
由图5可知,低压缸排汽焓的预测值随着负荷的变化规律与图4中实测值随着负荷的变化规律相似,均是低负荷工况下排汽焓波动加大,高负荷工况下排汽焓波动较小,负荷升高时排汽焓整体上升,但低压缸的排汽焓的预测值在高负荷工况时,逐渐偏向于稳定,在整个负荷工况下,排汽焓的预测值在2 406~2 412 kJ/kg范围内波动。
由图6可以进一步看出低压缸排汽焓的预测值与实测值变化规律相似,基于支持向量机的汽轮机低压缸排汽焓的预测值整体上都比实测值偏小,大约小10 kJ/kg左右,在工程允许的误差范围内,可见基于支持向量机的汽轮机排汽焓的预测值是有效的。

图6 排汽焓预测值和实测值
4 结论
本文利用支持向量机,建立了基于支持向量机的汽轮机排汽焓计算模型,将影响汽轮机排汽焓的主要因素作为输入变量,汽轮机排汽焓作为输出变量,建立模型,通过对模型的训练得到基于支持向量机的汽轮机排汽焓计算模型,便于在线监测中实时调用,从而在线计算汽轮机的排汽焓。该模型具有以下优点:
(1)实现了支持向量机对汽轮机排汽焓的计算,避免了传统算法的复杂性;
(2)由预测结果可知,随着锅炉负荷的上升,汽轮机排汽焓整体上保持上升,但变化不大。
本文的排汽焓计算模型是基于支持向量机的计算,如何对支持向量机模型进行优化还需进一步研究。

