2022年广州中考数学卷第25题的解法探究及启示

覃启艺

(广州市白云区华新学校,广东 广州 510440)

1 考题呈现

(2022 年广州市中考数学第 25 题) 如图1,在菱形ABCD中,∠BAD=120°时,AB=6,连接BD.

图1 2022年广州市中考数学第25题图

(1)求BD的长;

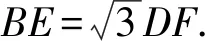
①当CE⊥AB时,求四边形ABEF的面积.

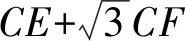
2 思路历程

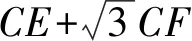
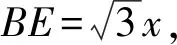
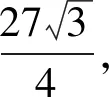
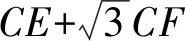
3 方法探究

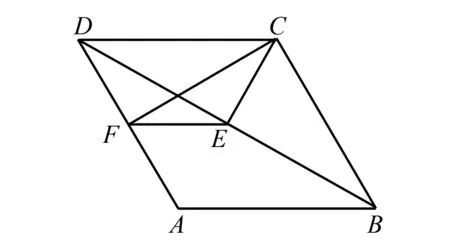
图2 思路1解析图

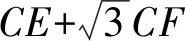
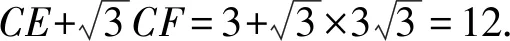
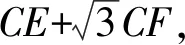
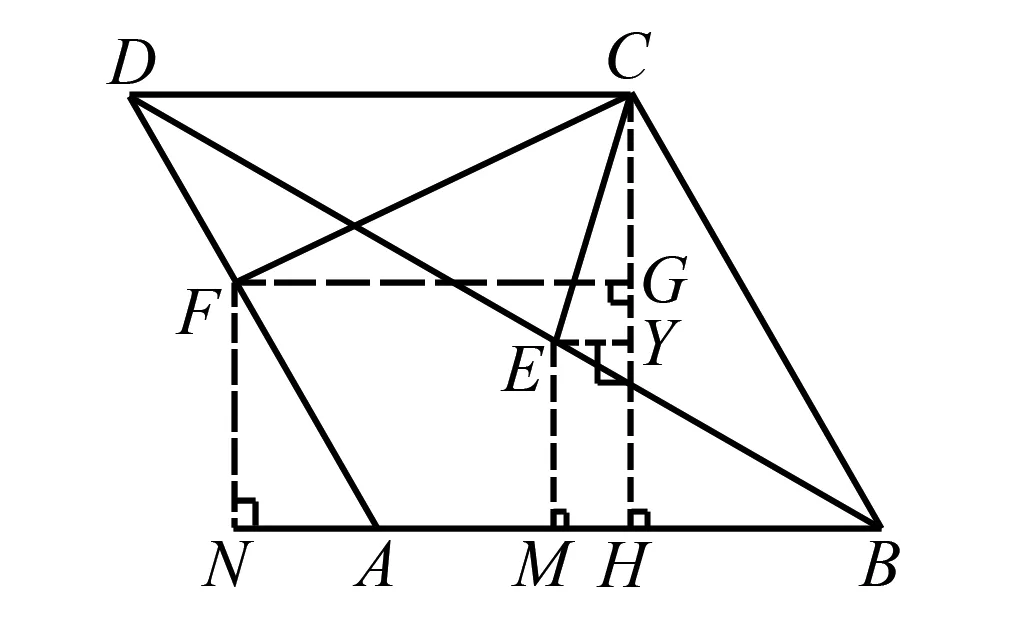
图3 思路2例题图

如图3,分别过点C、E、F作BA或其延长线的垂线,垂足分别为H、M、N,再过点F、E分别做CH的垂线,垂足为G、Y,则四边形FNHG为矩形.

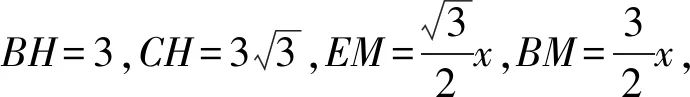
代入计算得:

≥3+9=12

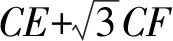
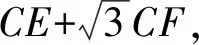
以BD为边作等边△DBP(如图4),在DB上找点G,使DG=BE,连接GP,CG,易得CG=CE.

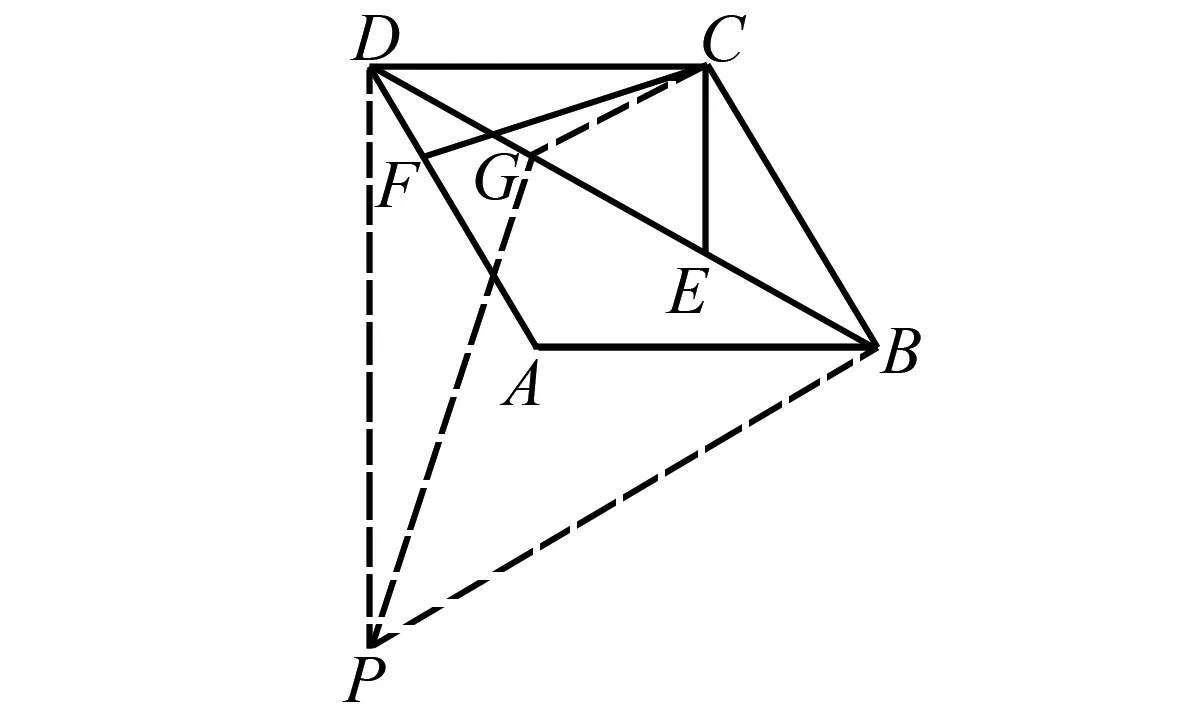
图4 思路3解析题图

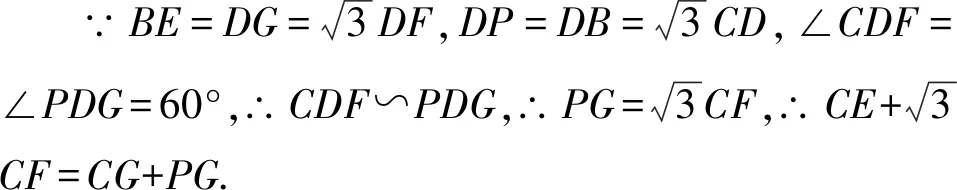
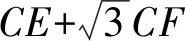
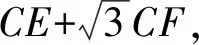
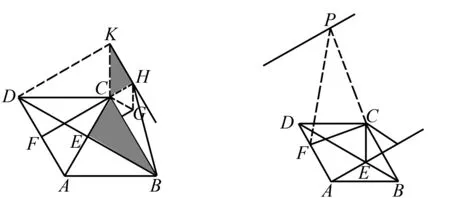
图5 思路2解析题图 图6 思路2扩展图

∴K为定点,∠HCK=∠ECB为定角,∴点H的轨迹为线段.

连接DK,易证∠CKD=60°,∠CDK=30°,DK⊥DA,且DK⊥KH,

∴KH∥AD.

∴当F、C、H共线且CF⊥AD时,CH+CF最小.下面只需求出CH+CF的最小值即可.

思路4利用余弦定理

在△CDF和△CBE中分别用余弦定理得:

CF2=DF2+CD2-2CD·DFcos60°=x2+36-6x=(x-3)2+27,

CE2=BE2+BC2-2BE·BCcos30°=3x2+36-18x=3(x-3)2+9,

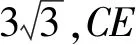
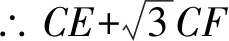
4 考点分析

本题可能涉及到的考点主要有:

几何动态:点E的运动变化,导致点F的变化,而相应的CE和CF的长度也发生变化.找准它们的变化规律是解决问题的关键.

几何最值:从形式上看,似乎是属于“胡不归模型”或者“阿氏圆模型”,如果套用这两个模型,就会误入雷区.它其实是一个拼接模型,拼接后应用“两点之间,线段最短”或者“垂线段最短”.

几何变换:在构造的过程中,对称变换、旋转变换是初中数学常考的考点,但利用相似变换去构造更加凸显解答此题的灵活性.作为部分数学较好的精英学生,研究此种变换恰好可以弥补我们学习数学的一个空缺.

三角函数:三角函数是解决三角几何问题的常用方法.特别是在特殊的直角三角形中,记住常用的特殊三角函数值,活用三角函数的知识,在解三角几何问题时有特殊的作用.

5 感悟与启示

中考要求学生掌握各方面的能力.从 2022 年广州中考数学 25 题中我们可以看出,广州中考非常重视对学生抽象能力、空间想象能力、运算能力和逻辑思维能力等数学核心素养的考查.

平时教学要重基础.基础知识是学生分数的生命线,我们一定要教育学生牢牢地打好基础,避免在简单的问题中出错.

考前复习要提能力.我们不难发现,大多学生在处理简单的几何题、运算题时毫无压力,而面对一些较难的综合题时便显得力不从心.问题在哪?他们经常是对简单的问题反复练习,而在难题上,经常是退却和自我否定的.因此,我们要告诫学生,提升自己综合能力的关键就是要认真细心、持之以恒地把难题做好做对,并在此基础上多吸收、多归纳、多反思.

学有余力要提前学.华南师范大学教授吴康老师提到:“高中的知识如余弦定理等在中考中可以直接使用.我们应该鼓励平时学有余力的精英同学,不应局限于初中的知识,还可以广泛涉猎更多更广的内容”.让学生主动思考,积极探索,这样就能站在一个相对的高度去看待问题,这其实就是一种数学核心素养的提升.