基于深度学习的初中数学单元复习课教学设计研究——以“三角形全等复习”为例

郑雪容

(福建省永泰县城关中学,福建 福州 350700)

深度学习是以“问题解决”为导向的学习过程,注重知识本质的学习与理解,学过的知识能长期记忆,还能加以迁移应用,强调学生学习的主动性.单元复习课是初中数学教学的重要课型之一,承担着知识的梳理整合、理解应用、拓展及思维发展和能力形成的主要任务.如何在初中数学单元复习课中落实学生的深度学习,是一线教师面临的一个教学难题,亟待解决.本文以“三角形全等”复习教学为例,从合适目标的制定、有效问题的设计等环节,浅析指向深度学习的初中数学单元复习课教学设计与思考.

1 基于深度学习的初中数学单元复习课的教学设计

1.1 教学目标是深度学习的指挥棒

教学目标引领着教学活动的开展,是深度学习的指挥棒.在“三角形全等”复习课教学设计时,考虑到整章内容多而细,一节课的时间内不可能做到面面俱到,从学生课前小测的数据发现,学生对全等三角形的性质和判定的简单应用掌握较好,但对于全等知识的深层次理解还不够,尤其涉及到SSA不能证明三角形全等的问题以及添加合适的辅助线构造全等问题都比较陌生.为此确定这节复习课深层次的教学目标为:灵活运用全等三角形的性质与判定方法;理解并掌握SSA不能判定三角形全等的原因;能够自主添加辅助线,构造合适的全等三角形解决问题.

1.2 课前小测是深度学习的前奏

课前小测是单元复习教学中十分必要的环节,能帮助教师及时、准确地了解学生掌握知识的真实情况,方便适时调整教学目标,为课堂教学做前期准备,是深度学习的引子.小测题的选择以考查基础与能力相结合的内容为主,能促进学生积极思考,小测结果最好能暴露出学生在单元学习中存在的问题,从而把它定为复习教学中要解决的核心问题.

在“三角形全等”复习课中,教师设计了课前小测题,旨在了解学生在应用“全等三角形性质及判定”解决“等角、等线”等问题中存在的困难.

(课前小测题)已知,如图1,△ABC中,①AB=AC,②BD=CD,③∠1=∠2,从①②③三个条件中,任选两个作为已知,另一个作为结论,组成命题,请写出所有的命题,并对正确的命题给出证明,错误的命题举出一个反例.

学生作答情况:

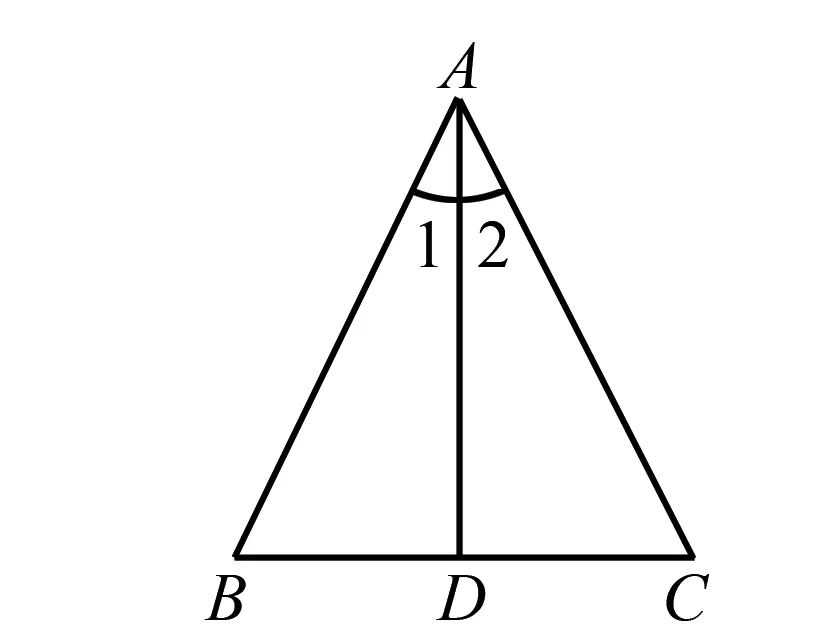
图1 课前小测题图

①②⟹③ 真 (SSS)

①③⟹② 真 (SAS)

②③⟹① 真?假?

从学生作答结果发现,学生对“SSA不能判定三角形全等”缺乏深层次理解,对“通过添加合适的辅助线解决几何问题”缺乏解题经验,于是教师把解决这两个问题作为本节课要突破的教学难点.

1.3 问题情境是深度学习的源泉

问题是学生求知欲望产生的必备因素,是深度学习的源泉.学生在学习中存在的疑惑,是最好的数学问题,教师要用心去发现,并引领学生去提炼、总结,最终形成有意义的数学问题,值得学生去探究、去解决.教师要引导学生围绕着这个核心问题,进行深层次地探究,进而深刻领悟数学思想方法,发展深层次的数学思维.

比如,在“三角形全等”复习导入环节,教师分析课前小测结果,借助多媒体展示几个有代表性的答案.

由于展示的是学生们自己的答案,课堂气氛一下子活跃起来,这时教师邀请A同学上台,分析解题思路,发现认知冲突,于是A同学意识到自己解错了.到此为此,全体同学都达成了共识(②③推①是假命题).当教师再问理由时,同学们都不假思索地回答:“因为SSA不能判定三角形全等.”(事实上,当三角形为直角三角形时,能够判定全等).这时教师引导学生观察图形,发现AB=AC可能是成立的,于是一系列疑问产生了:SSA不能判定三角形全等,那么②③推①究竟是真命题,还是假命题?SSA不能判定三角形全等的真正原因是什么?你能举一个反例吗?……这些都是学生感到疑惑、似懂非懂,但又迫切需要解决的问题,容易引起学生情绪的共鸣,激发学生参与探究、创新的积极性,促使学生进行深度思考.

1.4 合作探究是深度学习的主旋律

以教师讲授为主的课堂中,学生多半是被教师“牵着走”,学生的思维被绑架,缺少探究的主动性与积极性,学生获得的知识是老师硬塞给的,缺乏知识建构的过程,导致学生在知识的理解、应用、拓展等方面都有很大的局限.所以,在教学中,要以学生的学为主,通过师生合作、生生合作,共同完成问题的探究与解决,培养学生的能力[2].

在“三角形全等”复习课中,无论是导入部分的纠错、质疑,还是典例与习题的解答,以及每一次的归纳总结等环节,都充分体现了学生的主体地位,学生在教师的引导下,进行合作探究,解决关键问题,获得能力的培养.比如,案例中,当问题“SSA不能判定三角形全等的真正原因是什么?”提出之后,教师引导学生积极展开讨论,当有学生说“能判定直角三角形全等”,教师予以肯定(用HL能判定直角三角形全等),课堂的气氛热烈起来,于是“不能判定锐角三角形全等”“不能判定钝角三角形全等”……随着一个又一个的答案的出现,学生的思维一层又一层地被引向深处,这时,教师再引导学生动手画图(画出两边和其中一边对角确定的三角形)予以验证,学习逐渐进入深度思考与理解,最后达成共识(两边和其中一边对角确定的三角形不是唯一的,因此SSA不能判定三角形全等的原因是由于图形的不确定性造成的).

1.5 优化练习是深度学习的灵魂

复习课的练习是教学目标达成的关键,所以练习设计的恰当与否是至关重要的.指向深度学习的练习,要避免只重知识目标,而轻能力目标.练习的目的既要考查学生对知识技巧的掌握,也要重视学生思维的发展与能力的提升[3].题目不一定多,但要能体现知识间的关联,一道习题尽可能多地涉及多个知识点与能力点,通过“一题多解”“一题多变”“一题多思”等促进学生的深度思考,发展学生的发散思维与创新能力,使已有的知识得到有效迁移.

在“三角形全等”复习教学中,设计了一道课前小测题、一道例题、两道巩固习题.例题是课前小测的继续与深化,巩固习题是例题的应用和延伸,题量虽少,但却精,都是围绕着“全等三角形的性质与判定的灵活应用”展开的,能引起学生深层次地思考、探究,实现“做一题通一类”,真正掌握全等三角形相关知识.

例题已知,如图1,△ABC中,②BD=CD,③∠1=∠2,求证:①AB=AC.

由于例题是课前小测学生都错解的题目,再次出现,学生都特别兴奋,一副跃跃欲试的样子,能充分激发学生的探究欲望,从而进行积极思考.教师引导学生从条件出发,展开联想,弄清“要证什么?已知什么?还缺什么?构造什么?”之后,尝试添加合适的辅助线来解决问题.然后邀请学生上台展示不同解题思路.

思路一想用全等的知识来解决问题,但已有的条件无法证明三角形全等,要构造新的全等来解决问题.

方法1由条件BD=CD,想到AD是△ABC的中线,由三角形的中线联想到用“倍长中线法”构造全等.

方法2由条件∠1=∠2,想到AD是△ABC的角平分线,进而联想到“角平分线上的点到角两边的距离相等”,由“距离”自然想到过点D作垂线段构造全等.

思路二不用全等的知识,同样能解决问题.

方法3由条件BD=CD,想到AD是△ABC的中线,由此还可以想到“三角形中线等分三角形的面积”,再由“等积法”容易想到:过D分别作AB与AC边上的高即作垂线段解决问题.

练习1已知,如图2,△ABC中,∠C=90°,AC=BC,AD平分∠BAC,求证:AC+CD=AB.

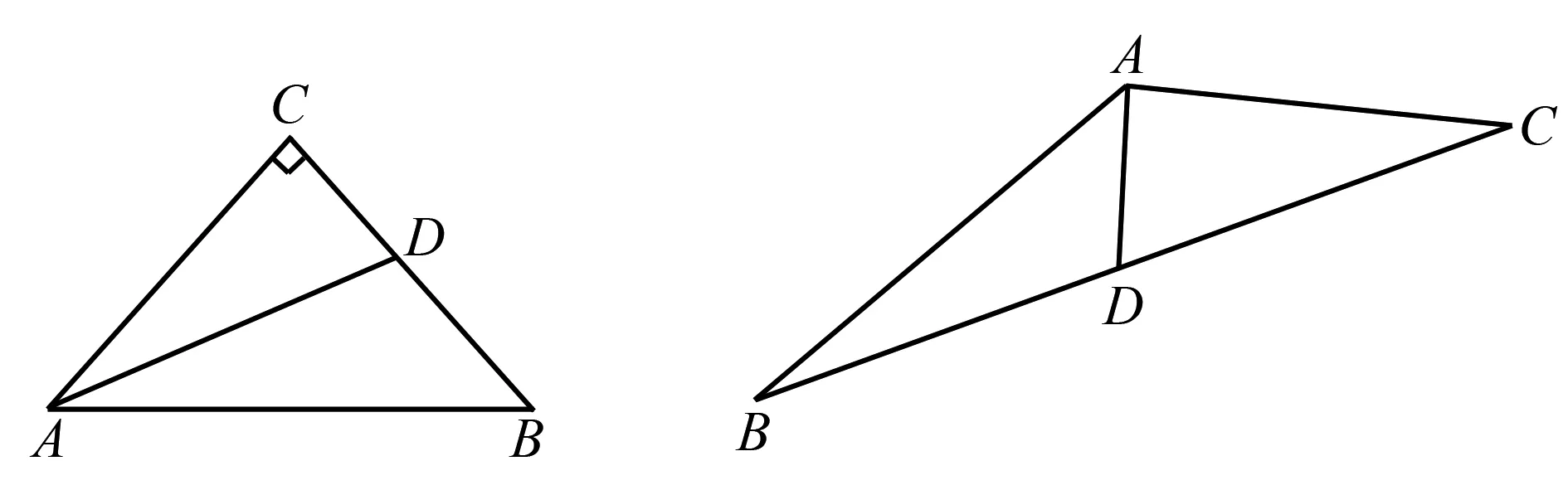
图2 练习1题图 图3 练习2题图

练习2已知,如图3,D是BC的中点,(1)求证:AB+AC>2AD;(2)若AB=8,AC=6,则AD的取值范围____.

两道习题是针对例题设计的,意在巩固学生掌握这类问题的解决方法,能内化为自身的能力.

1.6 归纳总结是深度学习的升华

总结和归纳在教学活动中起到画龙点睛的作用,使深入学习获得的知识、能力得到进一步的升华.在初中数学单元复习教学中,教师可以在教学的各个环节中适当地穿插小结,在帮助学生回顾建构知识的过程中,思维能力再一次得到锻炼提升.如“三角形全等”复习课中,在完成例题的解题思路梳理后,引导学生进行总结,从而形成知识经验(可以通过添加适当的辅助线,如倍长中线、作垂线段、截长补短等构造全等来解决需要用全等解决的问题),为知识的有效迁移起到关键性作用.

2 基于深度学习的初中数学单元复习课教学的思考

要在数学单元复习课中实现深度学习,简单地说,就是解决“要复习什么,要怎么复习,要达到怎样的深度?”的问题.深度教学,不能单纯地看成教得难、学得难.首先是在教师进行教学设计时,要充分考虑到学生现有的数学知识、数学思维与能力,存在的问题及要解决的问题,要生成的知识、能力及思维.其次,是在教师组织实施课堂教学时,要注重引导学生进行思考、主动参与合作探究,进而解决问题.

总之,问题是思维的起点,也是终点.在深度学习视角下,进行初中数学单元复习教学设计,要遵循“问题学生中来,能力学生中回”.教师要深挖学生疑惑,并围绕着“问题”主线,鼓励学生合作解决,在知识和技能的掌握中,促进学生思维从低阶向高阶发展,实现能力的提升.