构建开放性课堂 促进学生自觉体悟

李琳琳

开放性的课堂有利于提升学生的想象、发散、概括等思维能力，主动探究问题、自主解决问题的能力。其关键在于引导学生在具体课堂情境中进行自觉体悟，获得知识经验，提升思维品质。在立足课堂开放的基础上，以“一次函数、一元一次方程和一元一次不等式”为例，笔者对自觉数学课堂教学模式进行了实践与思考。

一、教学目标

经历一次函数、一元一次方程、一元一次不等式之间关系的探究过程，理解和掌握这三者之间的转化关系；在探究三者关系的过程中，体会方程、不等式、函数中蕴涵的模型思想，并且对这三种数学模型间的关系有本质的理解；在探究问题的过程中，感受数学模型的价值，体会数学知识之间的联系、数学与生活的联系，激发学生兴趣，培养学生执着的探究态度。

二、教学重难点

重点：理解并掌握一次函数、一元一次方程、一元一次不等式之间的关系，体会数学知识之间的联系。难点：结合图像理解一次函数、一元一次方程与一元一次不等式之间的关系。

三、教学过程

1. 自觉思考

师：同学们，开学以来我们主要学习了一元一次不等式，那么在这之前我们还学习过哪些和“一次”有关的数学知识？

生1：一次函数。

生2：一元一次方程，一元一次不等式组。

……

师：同学们回答得都很好，一次函数、一元一次方程和一元一次不等式之间有什么关系呢？今天我将和大家一起来探索它们之间的内在联系。

设计意图：这一环节的设计一方面在于激发学生的好奇心，进而产生学习的兴趣；另一方面让学生感到新内容是“有备”而来的，新内容是由数学知识的内部结构“自然生发”的，是“数学自身发展”的需要。

师：在生活中我们可能会遇到这样的情境。一根长20cm的弹簧，一端固定，另一端挂物体，在弹簧伸长后的长度不超过30cm的限度内，每挂1kg的物体，弹簧伸长0.5cm。如果所挂物体的质量是x kg，弹簧的长度是y cm，你能写出y与x之间的函数关系式吗？

生3：y=0.5x+20。

生4：我认为还要写出x的取值范围，20[≤]x[≤]30。

师：这两位同学回答得都很棒，在考虑实际问题的函数关系式时，我们通常要考虑自变量的取值范围。

设计意图：从熟悉的生活情境弹簧问题入手，引出本课的问题，回顾函数相关知识，同时使学生感受函数模型是探讨实际问题的基础模型；问题起点较低，全部学生都能够顺利、有效地进入课堂探讨氛围，让每个学生都有学好的信心。

2. 自主探究

师：刚才同学们成功列出了函数表达式，下面请同学们来求一求此弹簧所挂物体的最大质量，把你的想法写出来并和小组其他同学交流方法的异同。（教师巡视并对有困难的小组给予指导。）

设计意图：首先，让学生进行独立思考和探索，在自我尝试的过程中，提高自己分析问题和解决问题的能力；其次，小组内部的交流过程是学生思维火花的碰撞过程，可以帮助学生从多角度、多方面來思考问题，从而助推思维的提升。

师：同学们都用自己的方法求出了此弹簧所挂物体的最大质量，小组内有不同意见的请小组长来给大家展示小组成果。

生5： 因为弹簧伸长后的长度不超过30cm，所以0.5x+20[≤]30，得x[≤]20。所以最大质量为20kg。

生6： 因为弹簧伸长后的长度最大为30cm，弹簧最长的时候所挂的物体的质量是最大的，所以0.5x+20=30，得x=20，最大质量为20kg。

生7：还可以画出函数图像，通过观察图像来解决。

设计意图：将学生的方法和想法充分挖掘并进行比较，让学生感受不同方法之间的内在联系，初步感受函数、方程、不等式这些数学模型的关系并建立联系，体会数学方法和数学模型的本质。

师：下面，我们将方程和不等式这两种方法做比较，对于函数y=0.5x+20，方法①，当y=30时，0.5x+20=30，得x=20；方法②，当y[≤]30时，0.5x+20[≤]30，得x[≤]20。两种方法分别是借助一元一次方程和一元一次不等式解决的，那么请同学们观察这里的①和②，什么情况下可以借助方程来解决，什么情况下可借助不等式来解决呢？

生8：在函数表达式中，当一个变量的值确定时，可以利用一元一次方程来求另外一个变量的值。

生9：当一个变量的取值范围确定时，可以利用一元一次不等式来求另外一个变量的取值范围。

师：这两位同学总结得都很好，下面我们进行小组合作，小组长指定变量的值或取值范围，组员们合作求解另一个变量的值或取值范围。

（教师巡视小组合作的情况。）

设计意图：教师适时点拨和引导，充分展开新知的发生和发展过程，给学生足够的时间进行探索和交流。这里的交流不仅是师生的交流，生本的交流，更重要的是生生的交流。一方面让新知在自然而然的情况下渗透到学生的认知中，另一方面让团队合作的意识在学生头脑中树立起来。

师：通过刚才的合作，你们有什么疑问吗？

小组长1：对于一元一次方程中变量的确定，我们没有什么问题，但对于一元一次不等式，当我指定x<10时，我们小组在求解y的取值范围时遇到了困难。

师：你的问题提得太有价值了。哪位同学来帮他解答一下？

小组长2：先对函数表达式y=0.5x+20进行变形，用y来表示x为x=2y-40，再根据x<10，所以2y-40<10，得y<25。

师：这位同学解答得太棒了！以上我们从数值计算角度了解了这三个“一次”之间的关系，下面再让我们通过图像来观察三者关系的玄妙。

（教师利用PPT和几何画板展示。）

设计意图：教材上的内容比较浅显，此处借助动画从函数图像角度观察值确定和范围确定的内容是笔者在二次备课中添加进去的，一方面让学生感受数与形的结合，增强学生的形象思维能力，引导学生从直观的角度来深化新知；另一方面为解答九年级二次函数的综合性题目打基础，更好地培养学生借助图像来分析问题和解决问题的能力。

3. 自觉内化

师：下面就让我们试着用以上方法来解决一些问题。

例1 已知一次函数y=2x+4，（1）你能分别说出当y=0、y>0、y<0时，对应的x的值吗？（2）你还能写出当-2<y<8时，对应的x的值吗？

设计意图：使学生能够熟练运用数值计算的方法（借助一元一次方程、一元一次不等式和一元一次不等式组）来解决问题，进一步促进学生深入理解三个“一次”之间的关系这个核心知识。

4. 变式引领

例2 根据一次函数y=2x+4的图像，你能说出2x+4=0、2x+4>0、2x+4<0的解（或解集）吗？（图像略。）

变式1 根据一次函数y=2x+4的图像，你能说出2x+4=2、2x+4>2、2x+4<2的解（或解集）吗？（图像略。）

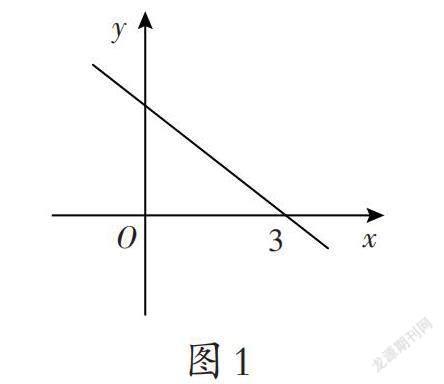
变式 2 如图1，函数y=ax+b，则ax+b=0的解为__________，ax+b≥0 的解集为__________， ax+b<0的解集为__________。

师：通过以上练习，你对三个“一次”又有了哪些新的理解？

生10：不用解方程和不等式，只要借助函数图像也可以解出一元一次方程和一元一次不等式。

设计意图：这里的变式引领是例1解法策略的变式，旨在引导学生借助函数图像来解决一元一次方程和一元一次不等式的问题。八年级的学生比较擅长利用数值计算解方程和不等式，对于借助图像来分析问题和解决问题的能力还比较薄弱。变式引领从简入难，打破学生思维上的封闭性，渗透数形结合的思想方法。尤其是变式2，只能借助图像来解决。

5. 回归生活

一艘轮船以20km/h的速度从甲港驶往160km远的乙港，2h后，一艘快艇以40km/h的速度也从甲港驶往乙港。（1）分别列出轮船行驶的路程（y1）和快艇行驶的路程（y2）与轮船时间（x）之间的函数表达式。（2）何时轮船行驶在快艇的前面？（3）哪一艘船先驶过60km处？哪一艘船先驶过120 km处？

设计意图：设置有一定生活背景的实际问题，让学生感受数学来自生活，数学也服务于生活，数学无处不在，进而增加学生学习数学的兴趣。同时，对于同一个背景，学生们给出了不同的解题方法。

6. 回归基础

让学生再次浏览教材，并完成课后练习。教师批改组长作业，组长批改小组成员作业，及时反馈。小组内部合作，对学有疑惑的学生进行及时点拨。

7.平等对话

师：通过本节课的探究，你有哪些收获？

生11：我明白了一元一次不等式、一元一次函数、一元一次不等式的关系。

师：你還掌握了哪些数学方法？

生12：数形结合的思想方法。

生13：转化的思想方法，比如：将函数的问题转化成方程或不等式问题。

师：大家总结得真棒！你还有哪些疑惑？

生14：一道题目既然可以用不同的方法进行解决，那么哪种方法比较简便呢？

师：同学们，你们对他的这个问题有哪些想法？

生15：直接解方程和不等式比较简单。

生16：我的看法不同，有的题目是不能直接解方程或不等式的，要借助函数图像。

生17：综合这两位同学的经验，我进行一个综合，要看具体的问题而定。如果题目中已经给出了图像就用图像的方法。

师：大家的发言都很精彩，老师都忍不住要为你们鼓掌了！

8.自觉生成

师：这节课的内容我们已经探究完了，现在请同学们将这节课中你最感兴趣的一道题仿编成一道新题，选择你喜欢的方法进行解答，并与同桌交流自己的想法。

五、教学反思

1. 以学生自主参与为基础，让学生获得体验

本节课的设计立足学生的“自觉学习”，通过一系列教学环节为学生量身打造更加符合学生认知规律的课堂，把核心知识的探究交给学生。本节课由熟悉的弹簧问题，引出问题，回顾函数相关知识，同时使学生感受函数模型是探讨实际问题的基础模型；问题起点较低，吸引全部的学生都能够顺利、有效地进入课堂探讨氛围，让每个学生都有学好的信心。

2. 以学生活动思考为主线，让学生主动建构

独立探索、小组合作、组间互助、平等对话，本节课用这些学习方式的有机融合来提升学生的学习力，让学生的学习有趣、有味，同时也达到了活动“动而有得”的目的。在学生活动中，不仅充斥着学生们别样的激情和灵气，更体现了学生的活力和创造力，有助于造就学生良好的阳光品质。

3. 以学生获取知识为目的，让学生形成技能

“学生获取知识”和“教师完美讲授”，两者何为课堂的重心？笔者更赞同的是前者，《义务教育数学课程标准（2022年版）》强调的也是学生获取知识和形成技能。本节课的各个环节均立足于学生对知识的接受程度，以学生的“学”来确定教师应当如何“教”。环节“变式引领”则让学生在获取知识的基础上，形成真正属于自己的技能。另外，函数图像的强化，则更多地考虑学生的长远发展，提高学生借助图像分析问题的能力。

4. 以学生经历过程为根本，让学生获得发展

在环节“自觉思考、自主探索、自觉内化、回归生活、回归基础”中，学生可以充分体会数学知识的形成与发展过程。数学知识的发展不是零碎的，也不是空降的，而是遵循着一定的规律自然而然生成的，这也有利于学生建立自己的知识模块。

（作者单位：江苏省常州市丽华中学）