一道中考题的探究*

广东省深圳市光明区华夏中学 (518107) 蒋红珠

华南师范大学数学科学学院 (510631) 黄文丽

内江师范学院数学与信息科学学院 (641100) 刘成龙

试题再现(2020年深圳中考第16题(下文简称16题))如图1，已知四边形ABCD，AC与BD相交于点

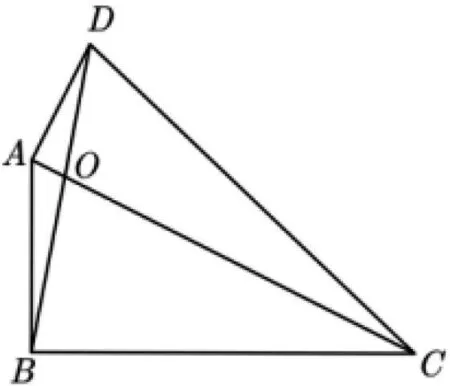
图1

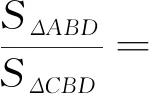
16题以直角三角形构成的四边形为载体，主要考查学生对常见相似三角形相关模型的掌握程度，考查学生对面积比问题的转化与解决能力，具有言语直观、构思精巧、图形简洁、内涵丰富、背景公平、解法多样等特点，是考查学生逻辑推理、直观想象、数学建模、数学运算等素养的有力素材．同时，16题是数学探究的良好素材．下文将从试题的背景、解法和变式三个视角进行探究．

1 背景探究

研究试题背景可以准确把握试题的本质、理解试题的设问、扩宽试题的解法、加强试题的扩展．中考数学压轴题追求试题背景的新颖性与独特性，常常是在“教材知识”的基础上向四大背景上集中：高中数学背景、现实生活背景、历史名题背景、经典试题背景(包括往年的竞赛题或中考题)．16题蕴涵教材背景和竞赛背景．

背景1教材背景

源于北师大版九年级上册第三章《图形的相似》复习题中的第22题(第107页):

第22题如图2，AB⊥BD，CD⊥BD，AB=6，CD=4，BD=14，点P在BD上移动，当以P，C，D为顶点的三角形与ΔABP相似时，求PB的长．

评注：第22题中当以P，C，D为顶点的三角形与ΔABP相似时，就可提炼出“一线三等角模型”中的“一线三直角模型”，是相似三角形中的重要模型．在16题的图1中，过点D作BC的平行线与BA的延长线交于点E，如图3所示，通过16题的其他条件可知∠E=∠ABC=∠DAC=90°，即含有“一线三直角模型”．命题者间接选择“一线三直角模型”为素材，为ΔABD和ΔCBD求面积找底和高奠定了基础，考查学生转化与化归思想及数形结合思想．

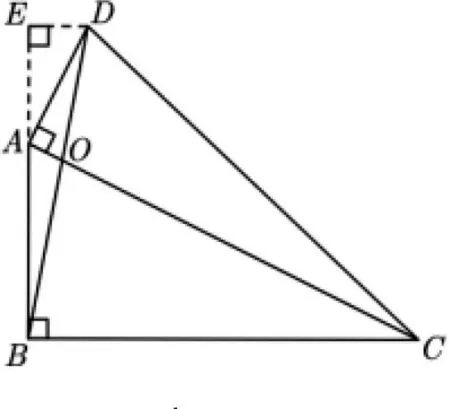
图3

背景2竞赛背景

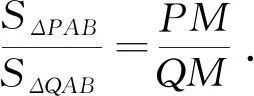
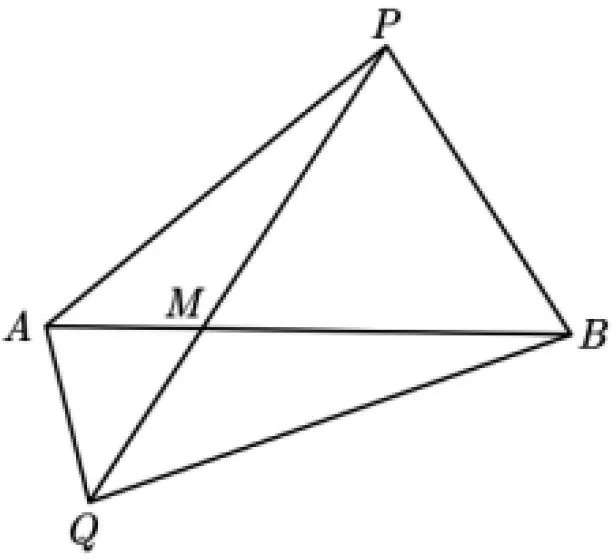
(1)

2 解法探究

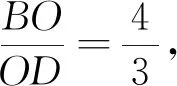
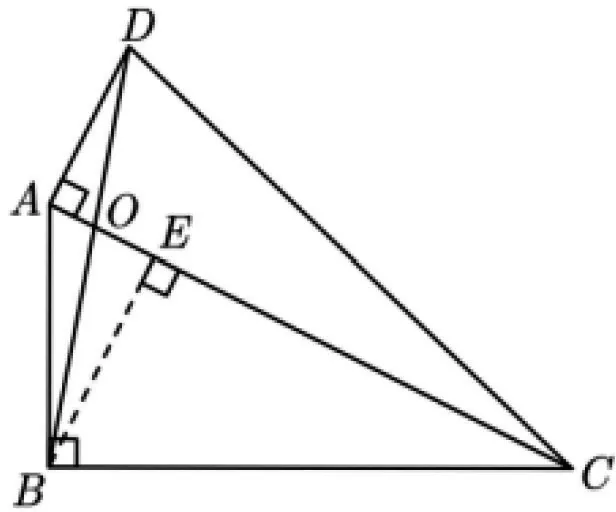
图5

评注：解法1主要使用了相似三角形的性质来解答问题，解法1后面求OC时，也可使用射影定理来求．

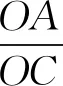
解法2：如图6，过点D作BC的平行线与BA的延长线交于点E，过点O作AB的垂线交AB于点F，由∠ABC=∠DAC=90°，则易证ΔAED～ΔOFA～ΔCBA且ΔAFO～ΔDEB．因为

图6

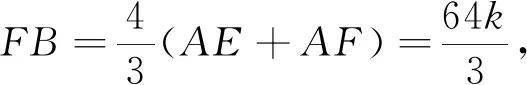
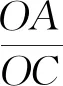
思路3 解法1和解法2都主要通过相似三角形的性质来解答的，而构造相似三角形的一个重要方法就是作平行线，构造“8”字模型．

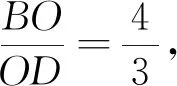
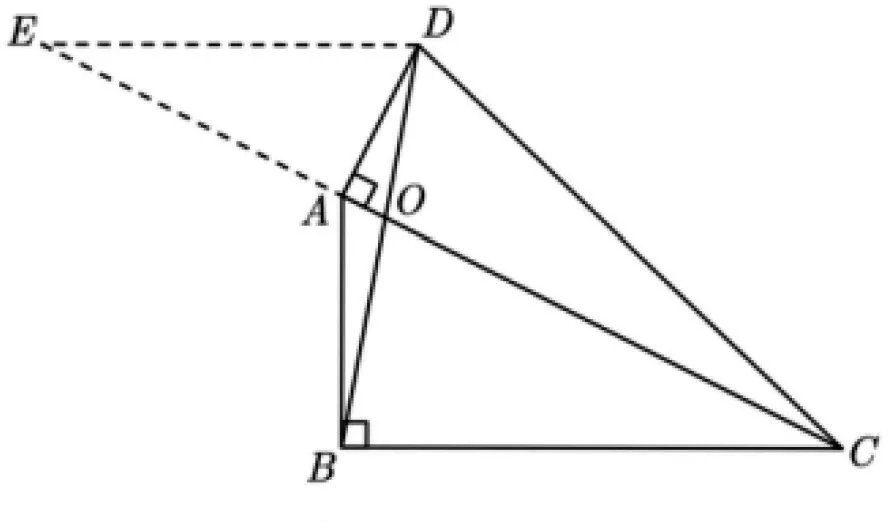
图7

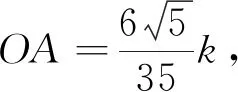
评注：解法3利用作平行线构造相似三角形，在求解OA与OC的比值过程中主要使用方程的思想．

思路4 求两个三角形的面积之比时，更为直接的想法是用底和高的乘积将其表示出来．

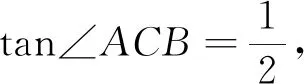
图8

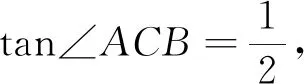
评注：解法4和解法5解答原理一样，只是寻找ΔABD和ΔCBD不同的底和高而已．

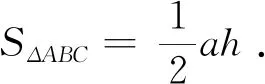
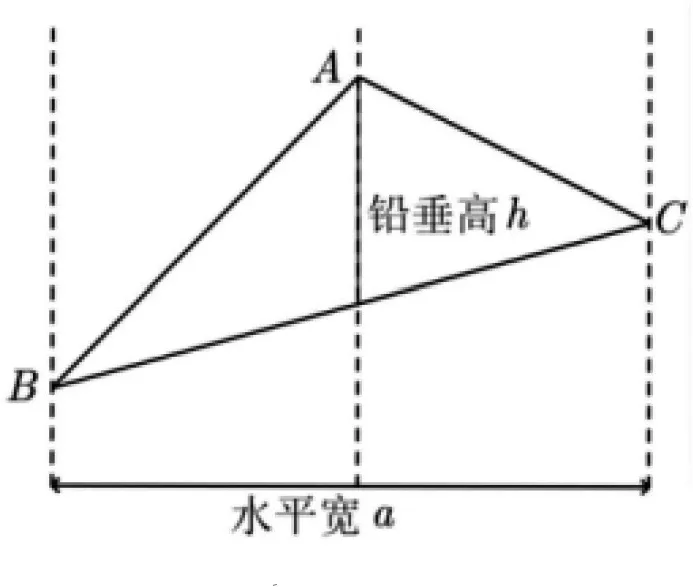
图9

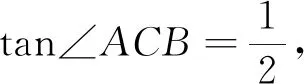
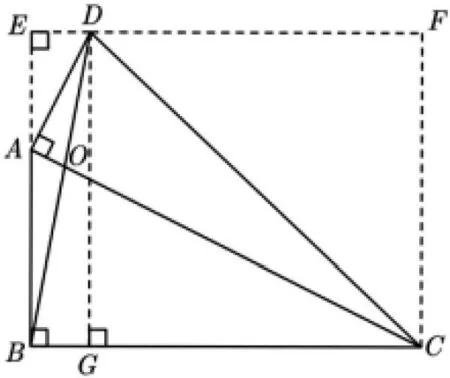
图10

评注：解法6与解法4、5后续的解答过程类似．

思路6 由图10，考虑用割补法求三角形的面积．针对ΔABD，比较好算的是采用补形法，即SΔABD=SΔBED-SΔAED．求ΔCBD的面积时，则有如下4种方法．

解法7：SΔCBD=S梯形ΔEBCD-SΔEBD．

解法8：SΔCBD=S梯形ΔEBCD-SΔABD-SΔEAD．

解法9：SΔCBD=SΔBDG+SΔCDG．

解法10：SΔCBD=S矩形EBCF-SΔEBD-SΔDFC．

评注：由解法2易得解法7、8、9、10中所出现的三角形、梯形、矩形的面积，此处不再赘述．

3 变式探究

思路1 已知OB与OD的比值和AB与BC的比值，求OA与OC的比值和AD与AC的比值．

变式1 如图11，已知四边形ABCD，AC与BD相交于点

求证

变式1的证明由16题的解法1易证出．

思路2 已知OA与OC的比值和AB与BC的比值，去求OB与OD的比值和AD与AC的比值．

变式2 如图11，已知四边形ABCD，AC与BD相交于点

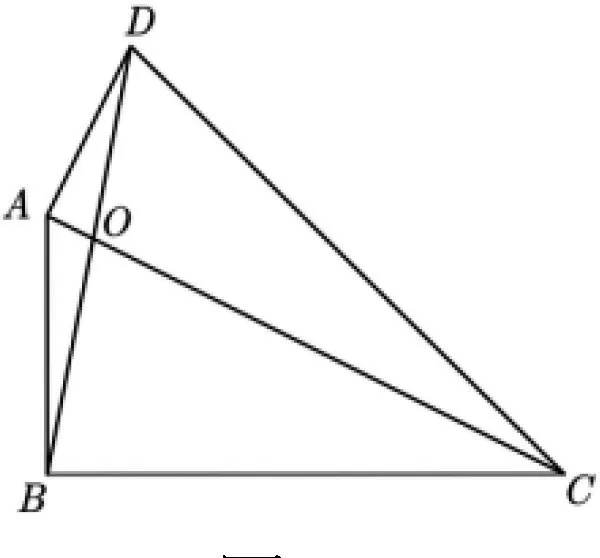
图11

求证

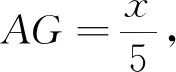
图12

思路3 已知OB与OD的比值和AD与AC的比值，去求OA与OC的比值和AB与BC的比值．

变式3 如图13，已知四边形ABCD，AC与BD相交于点

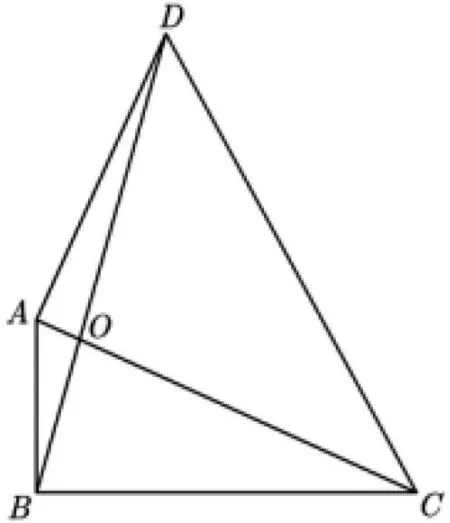
图13

求证

简证：如图14，设AD=3x，则

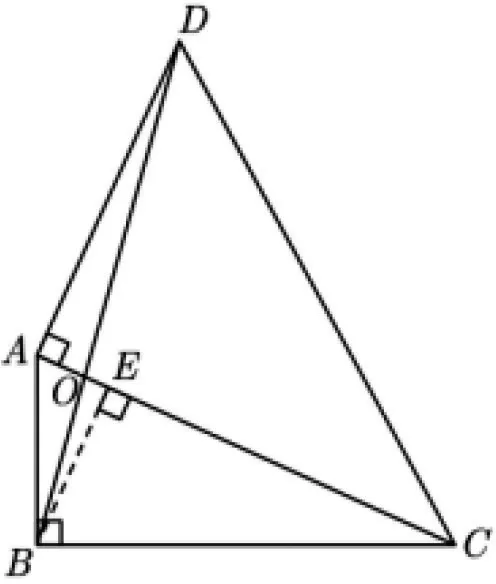
图14

思路4 已知OA与OC的比值和AD与AC的比值，去求OB与OD的比值和AB与BC的比值．

变式4 如图15，已知四边形ABCD，AC与BD相交于点

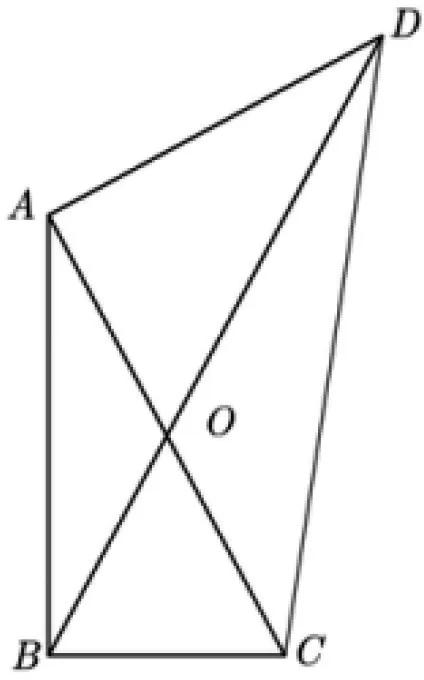
图15

求证

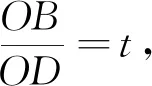
思路5 在背景探究中揭示了本题蕴含的“一线三直角模型”，若图1中的∠ABC和∠DAC不是直角，结论会怎样？于是得到如下推广．

变式5 如图16，已知四边形ABCD，AC与BD相交于点

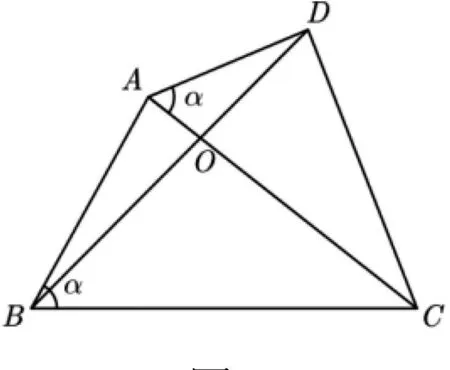
图16

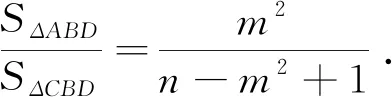
简证：过点B作AD的平行线与AC相交，方法类似于解法探究中的解法1．

评注：为了描述的简便性，在RtΔDAC和RtΔABC为载体的四边形ABCD中，称OB与OD的比值和OA与OC的比值为“内边比”、称AB与BC的比值、AD与AC的比值为“直角三角形的外边比”．从变式1、2、3、4可知，只要已知任意一组“内边比”和一组“直角三角形的外边比”，就可求出另一组“内边比”和另一组“直角三角形的外边比”．变式5让16题更具一般性．