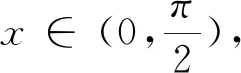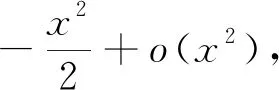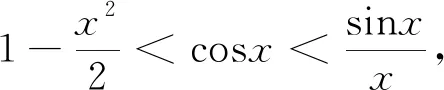2022年新高考Ⅰ卷第7题的命题手法探究*
福建省泉州市第七中学 (362000) 黄永生 杨 丹
1 题目
(2022年新高考Ⅰ卷T7)已知
c=-ln0.9,则a,b,c的大小关系是( ).
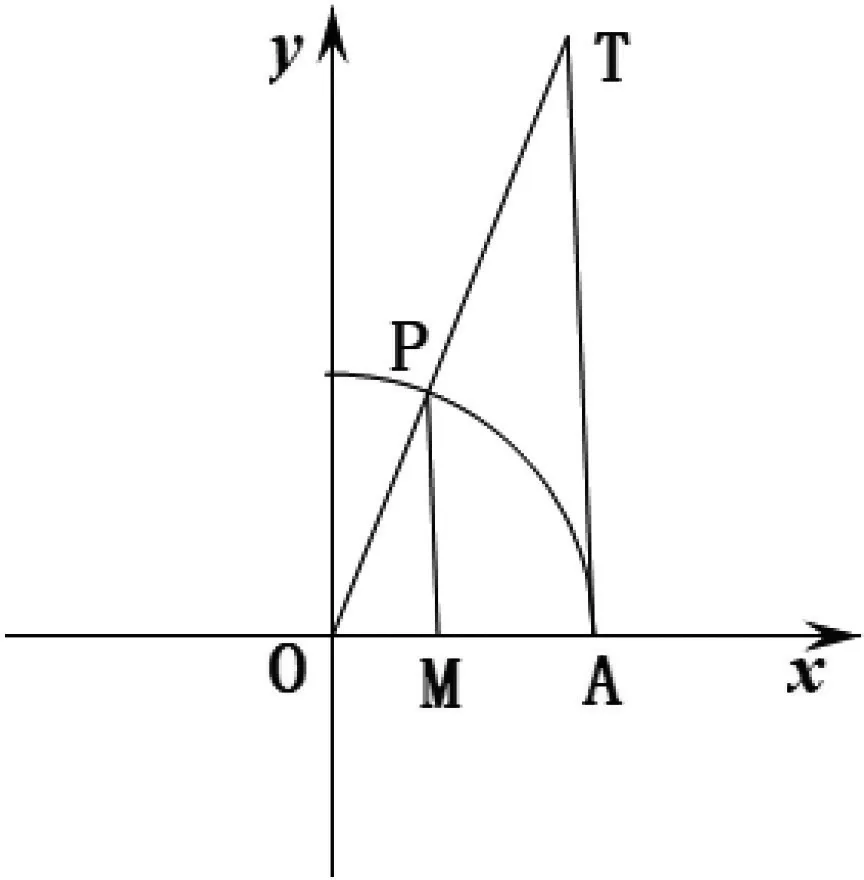
A.a C.c 在x=0.1的函数值. 解答:令 综上c 对于上述试题,命题者先构造函数y=f(x),通过导数研究f(x)的单调性与最值,进一步得到不等式.为增加试题的难度,命题者同时构造多个函数,构成不等式链,并对不等式中的变量x赋值,放缩变形,得到若干个实数的大小关系.常见的不等式链有: 等.同时通过指数对数运算互化,可以得到有关指数函数的不等式链. 如图1,构造单位圆在第一象限的部分,记 在江河湖泊设置入河排污口的建设项目,建设单位应当取得县级以上地方人民政府水行政主管部门或者流域管理机构出具的入河排污口设置同意文件。在进行入河排污口设置审批时,应结合废污水产排分析及纳污水域调查成果,分析判断其是否符合清洁生产、达标排放与总量控制、水功能区限排等方面要求。因保留区、缓冲区主要是采用现状污染物入河量作为纳污能力及限排总量,因此在进行入河排污口设置审批时,需削减水功能区内相应的排污量,以满足新增加入河排污量后不会超过限排总量;而开发利用区的纳污能力及限排总量主要是采用模型法进行计算,新增加入河排污量与现有入河排污量的总和不得超过该水功能区限排总量。 图1 新题1 已知 则a,b,c的大小关系是( ). A.a C.c 新题2 已知 则a,b,c的大小关系是( ). A.a C.c 新题3已知 则a,b,c的大小关系是( ). A.a C.c 新题2,3的编制手法大同小异,相信基于此背景可创作出更加新颖的试题,其解答与新题1 的解答类似,此处不再赘述.有兴趣的读者可以构造其他的函数,通过赋值、等价变形、放缩等手段进行新题编制探究.2 解法思考
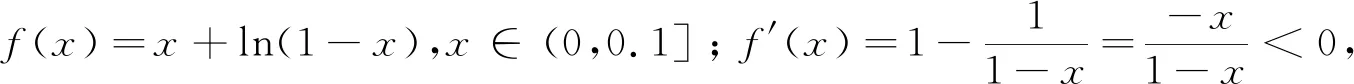
3 命题手法探究
4 新题命制