《导数》专题训练

木萍萍

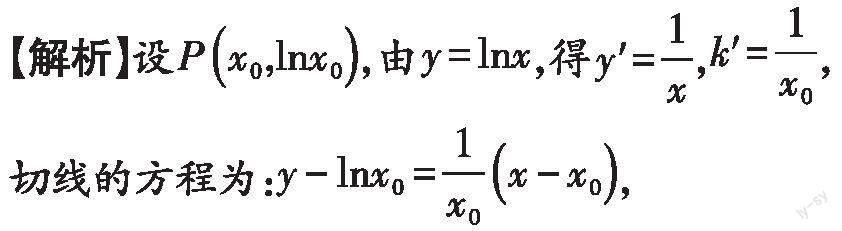
一、单选题

1. 曲线[y=xex+2x-2]在[x=0]处的切线方程是（     ）

A. [3x+y+2=0] B. [2x+y+2=0]

C. [2x-y-2=0] D. [3x-y-2=0]

A. （-1，1）      B. （0，1）       C. （1，+∞）      D. （0，2）

3. 已知函数[f（x）=x2+2cosx]，设[a=f（20.5）]，[b=f0.52]，[c=f（log0.52）]，则（     ）

A. [a>c>b]    B. [a>b>c]    C. [c>b>a]    D. [c>a>b]

A. 2        B. 1        C. 0        D. -1

二、多选题

8. 已知函数[fx=alnx+x]，[gx=sinx]，若[hx=fx-gx]，则下列说法正确的是（     ）

A. 当[a=-1]时， [fx]有2个零点

B. 当[a=0]时， [fx]恒在[gx]的上方

C. 若[hx]在[0，+∞]上单调递增，则[a≥0]

A. 函数[fx]的图象关于点[0，1]中心对称；

B. 函数[fx]无零点；

D. 曲线[y=fx]的切线都不过点[0，0]

三、填空题

13. 若函数[f（x）=kx-ex]有两个零点，则[k]的取值范围为______．

四、解答题

14. 已知函数[fx=aex-exa≠0]．

（1）讨论[fx]的单调性：

（2）若[fx>x+1]对[x∈2，+∞]恒成立，求[a]的取值范围．

15. 已知函数[fx=3x-a+1lnx，gx=x2-ax+4].

（1）若函数[y=fx+gx]在其定义域内单调递增，求实数[a]的取值范围；

（2）是否存在实数[a]，使得函数[y=fx-gx]的图象与[x]轴相切？若存在，求满足条件的[a]的取值范围，请说明理由．

（1）当[m=2]时，试判断函数[f（x）]在[（π，+∞）]上的单调性；

（2）存在[x1，x2∈（0，+∞）]，[x1≠x2]，[fx1=fx2]，求证：[x1x2

参考答案与解析

一、单选题

1．【答案】D

【解析】[y=xex+2x-2]，则[y=（x+1）ex+2]，当[x=0]时，[y=-2]，[y=3]，

所以切线的方程为[y--2=3x]，即[3x-y-2=0].故选D．

2．【答案】B

【解析】 [f（x）]的定義域为（0，+∞），

可得[0

3．【答案】A

【解析】 [f（x）=x2+2cosx]的定义域为R，

[f（-x）=（-x）2+2cos（-x）=x2+2cosx=f（x）]，

所以[f（x）]是偶函数，

[f（x）=2x-2sinx]，令[g（x）=2x-2sinx]，

则[g（x）=2-2cos≥0]，

所以在R上[f（x）]单调递增， [f（0）=0]，

即在（0，+∞）上[f（x）>0]， [f（x）]单调递增，

因为[c=f（log0.52）=f（-1）=f（1）]，[20.5>1>0.52]，

所以[f（20.5）>f（1）>f（0.52）]，即[a>c>b]，故选A.

4．【答案】B

令[x=0]，[y=lnx0-1]，则[N0，lnx0-1]，

过P作x轴的垂线，垂足为M，如图1所示.

得[4ln4=x0lnx0-x0+4]，

显然[x0=4]是该方程的一个根，

设[g（x）=xlnx-x+4-4ln4]，得[g（x）=lnx]，

由题意可知：[x>1]，所以[g（x）>0]，此时函数单调递增，

故方程[4ln4=x0lnx0-x0+4]有唯一实根，

5．【答案】C

【解析】[∵fe=e0+e-e=1]，即[x1=e]，

由[gx2=1]，即[lnx2-ax2-ea+4=1]，

[∴ymax=1-lne-2=-2<0]，即[hx<0]在[e，e2]上恒成立，[∴hx]在[e，e2]上单调递减，

6．【答案】C

7．【答案】A

[g（x1）>g（x2）>0]，即[g（x1）-g（x2）>0]，

原不等式恒成立可化为[mg（x1）-mg（x2）>x1f（x1）-x2f（x2）]恒成立，

当[x1>x2>0]时，[mg（x1）-x1f（x1）>mg（x2）-x2f（x2）]恒成立，

所以[h（x）=mx2-lnx-1≥0]在（0，+∞）上恒成立，

由[m∈Z]知，整数m的最小值为2.故选A.

二、多选题

8.【答案】BC

对于选项B，当[a=0]时，[hx=fx-gx=x-sinx]，则[hx=1-cosx≥0]，所以[hx]在[0，+∞]上单调递增，且[hx>0]，即[fx>gx]，所以B选项正确；

一个极值点，所以D选项错误.故选BC．

9.【答案】AC

故选AC.

10.【答案】BC

=1-e-2>0]，所以函数[gx]无零点，因此方程无实数解，假设不成立，故D正确.故答案为BC.

三、填空题

12．【答案】[-e]

所以[g（x）>0， g（x）]单调递增，

所以[g（x）<0， g（x）]单调递减，

此时直线OP的方程为[y=-x]，设直线[y=-x]与曲线[y=alnx]相切于点[（x0，alnx0）]，

显然[（x0，alnx0）]在直线[y=-x]上，

则[alnx0=-x0]，因此[aln（-a）=a，即a=-e].

13．【答案】[e，+∞]

所以当[x∈-∞，1]时，[g'x>0]，[gx]单调递增；当[x∈1，+∞]时，[g'x<0]，[gx]单调递减；

四、解答题

14.【解析】（1）函数的定义域为[R]， [fx=aex-e]．

当[a>0]时，令[fx>0]，得[x>1]，令[fx<0]，得[x<1]；

当[a<0]时，令[fx>0]，得[x<1]，令[fx<0]，得[x>1]．

综上，当[a>0]时，[fx]在[-∞，1]上单调递减，在[1，+∞]上单调递增；

当[a<0]时，[ fx]在[-∞，1]上单调递增，在[1，+∞]上单调递减．

（2）由（1）知，函数[gx=ex-ex]在[2，+∞]上单调递增，

则[gx≥g2=ee-2>0]，

设[px=e-xexx≥2]，则[px=-x+1ex<0]，则[px]在[2，+∞]上单调递减，

所以[px≤p2=e-2e2<0]，则[hx<0]，

所以[hx]在[2，+∞]上单调递减，

15.【解析】（1）[y=fx+gx=3x-a+1lnx+x2-ax+4]在[（0，+∞）]上单调递增，

（2）函数[y=fx-gx=3x-a+1lnx-x2+ax-4]，

设[hx=3x-a+1lnx-x2+ax-4，x>0]，

①当[a+1≤0]时，即[a≤-1]时，当[x∈0，1]时，[h′x>0]，当[x∈（1，+∞）]时，[h′x<0]，

∴[hx]在[0，1]上单调递增，在[（1，+∞）]上单调递减，

∴[hxmax=h1=a-2=0]，解得[a=2]（舍去），

②当[a>-1]时，[h′x=0]，

∵函数[y=fx-gx]的图象与[x]轴相切，

当[h1=0]时，[h1=a-2=0]，解得[a=2]，

∴[3t-2tlnt-t2+2t-1t-4=0]，

即[t2+2t-2tlnt-4=0]，

设[φt=t2+2t-2tlnt-4，t>0]，

∴[φ′t=2t+2-21+lnt=2t-lnt]，

当[0

当[t>1]时，[m′t>0]，函数[mt]单调递增，

∴[mt≥m1=0]，∴[φ′t≥0]，

∴[φt]在[（0，+∞）]上单调递增，

∵[φ1=-1<0，φ2=4-4ln2>0]，

∴存在[t0∈1，2]，使得[φ（t0）=0]，

综上所述存在实数一个实数[a∈1，3]，得使得函数[y=fx-gx]的图象与[x]轴相切．

所以当[m=2]时，函数[f（x）]在[（π，+∞）]上单调递增.

（2）不妨设[0

设[g（x）=x-sinx]，得[g（x）=1-cosx≥0]，所以[g（x）]在[（0，+∞）]上為增函数，

则[x2-sinx2>x1-sinx1]，所以[x2-x1>sinx2-sinx1]，

[∴][h（t）]在[（1，+∞）]单调递减，