由一道题谈抛物线问题的解法
2023-03-31 05:48马小鹏
语数外学习·高中版下旬 2023年12期
马小鹏
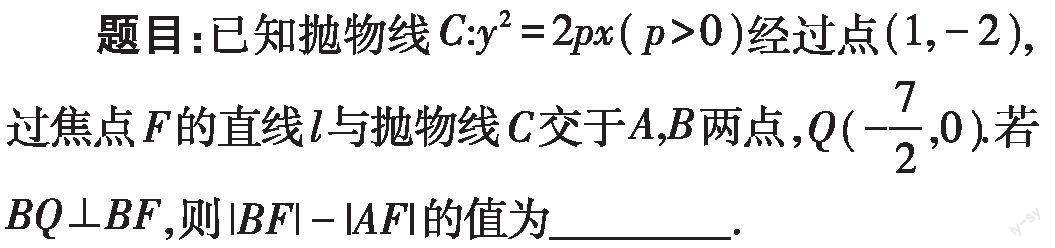
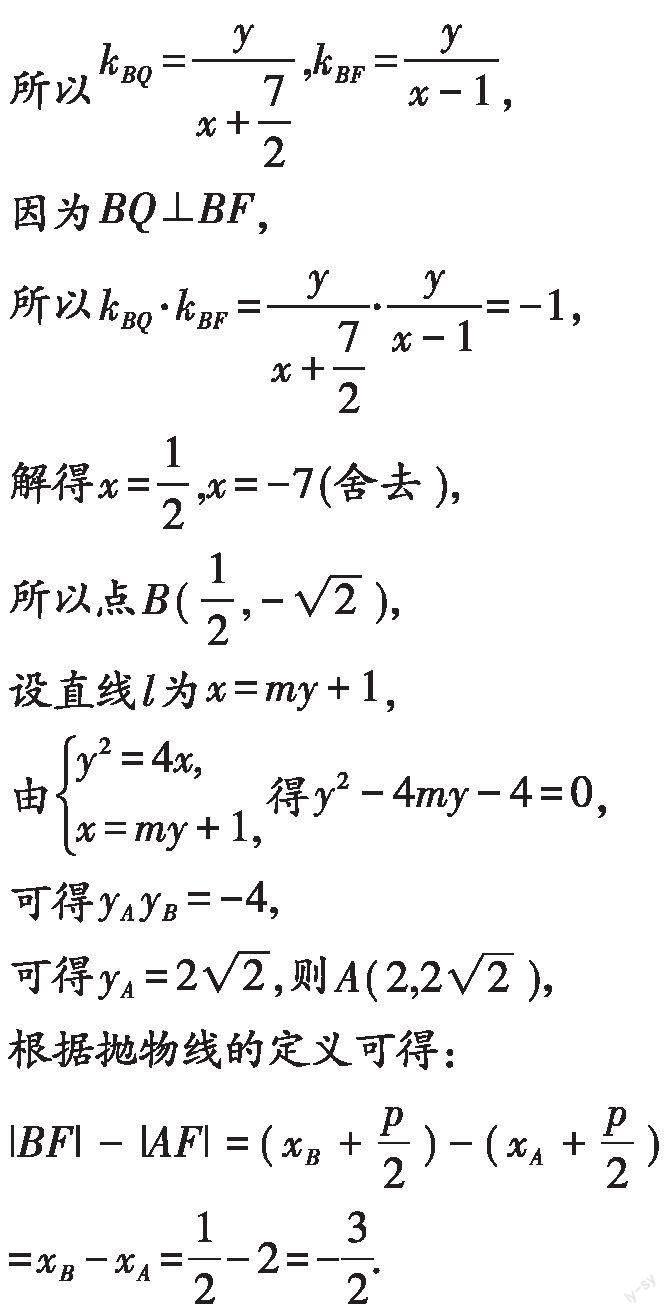

抛物线问題经常出现在各类试题中.这类问题主要考查抛物线的定义、几何性质、标准方程的应用.下面结合一道抛物线问题,研讨一下解答此类问题的方法、思路.
一、定义法
定义法是解答数学问题的重要方法.在解答抛物线问题时,根据抛物线的定义,可快速建立抛物线上的点到焦点与到准线之间的距离的关系,从而快速确定动点的轨迹方程.
解:由题意可知[C:y2=4x],
则[F(1,0)],设点[B(x,y)],
我们先根据[BQ⊥BF]求得B的坐标;然后根据韦达定理求得A点的坐标,即可根据抛物线的定义:抛物线上的点到焦点的距离与到准线的距离相等,求得[|BF|]、[|AF|],从而求得问题的答案.一般地,对于与抛物线焦点弦有关的问题,都可以考虑运用抛物线的定义建立焦点弦之间的关系式,这样能有效地减少运算量,提升解题的效率.
二、向量法
对于解析几何问题,有时可以根据线段之间的关系构造向量,这样便可利用向量的运算法则,如加减、数乘运算法则,根据向量的数量积公式、模的公式等快速建立关系式,顺利求得问题的答案.
解:由题意可知[C:y2=4x],则[F(1,0)],
将[BQ⊥BF]用向量表示出来,即可快速建立关于B点坐标的关系式,从而求得B点的坐标,进而求得[|BF|、|AF|].运用向量知识解题,不仅可以将焦点弦和过焦点的直线的倾斜角联系起来,还能得到一系列关于直线的斜率和焦半径长度有关的结论,这样能大大简化运算.
总的来说,要想提升解答抛物线问题的效率,不仅需要掌握抛物线的定义、性质、方程,还需将其与向量、三角函数知识关联起来,快速建立关系式.
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08
小资CHIC!ELEGANCE(2022年1期)2022-01-11
语数外学习·高中版中旬(2021年1期)2021-09-10
南方周末(2018-03-08)2018-03-08
科学中国人(2017年22期)2018-01-02
中学化学(2017年6期)2017-10-16
中学生数理化·七年级数学人教版(2016年4期)2016-11-19
摄影之友(2016年8期)2016-05-14
淮北师范大学学报(自然科学版)(2014年4期)2014-07-04
湖南理工学院学报(自然科学版)(2014年1期)2014-02-28

