怎样由函数零点的个数求参数的取值范围

周理国

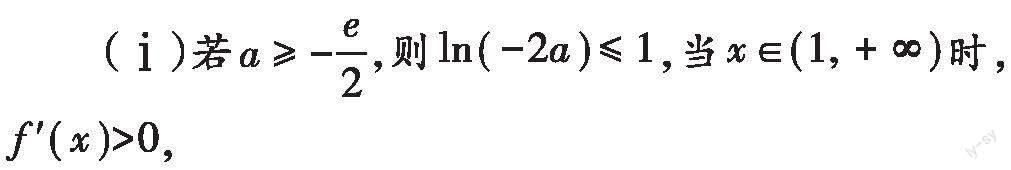
由函数零点的个数求参数的取值范围问题通常具有较强的综合性.这类问题往往侧重于考查函数的单调性、奇偶性、对称性、周期性、图象，方程的根的分布，以及零点存在性定理.下面结合例题，谈一谈怎样由函数零点的个数求参数的取值范围.

一、利用零点存在性定理

零点存在性定理：如果函数[y=f（x）]在[[a，b]]上的图象是一条连续不断的曲线，且有[f（a）f（b）<0]，则函数[y=f（x）]在[（a，b）]内至少有一个零点.由函数零点的个数求参数的取值范围，往往要先判断出函数在各个区间上的单调性；然后根据零点存在性定理建立不等关系式，从而求得参数的取值范围.

因为[g（x）>0]，所以函数[y=g（x）]在[（-∞，0]]和[（0，+∞）]上均是单调递增函数.

而在区间[（0，+∞）]上，当[x→0]时，[g（x）→-∞]；当[x→+∞]，[g（x）→+∞].

因此函数[y=g（x）]在区间[（0，+∞）]上存在1个零点，那么另1个零点必定在区间[（-∞，0]]上.

而在区间[（-∞，0]]上，当[x→-∞]时，[g（x）→-∞]，

由零点存在性定理可知[g（0）=1+a≥0]，

解得[a≥-1]，

综上所述，要使[g（x）]存在2个零点，需使[a≥-1].

对函数[g（x）]求导，即可根据导函数与函数单调性之间的关系判断出函数在[（-∞，0]]和[（0，+∞）]上的单调性.而当[x→-∞]时，[g（x）→-∞]，即在[（0，+∞）]上的函数值均小于0，由零点存在性定理可知，要使[gx]在区间[（-∞，0]]上存在1个零点，需使[g（0）≥0].

例2.已知函数[f（x）=（x-2）ex+a（x-1）2]有2个零点，求[a]的取值范围.

解：函数[f（x）]的定义域为[R]，求导得[f（x）=（x-1）?] [（ex+2a）]，

（1）当[a=0]时， [f（x）=（x-2）ex]有唯一的零点[2]，不符合题意；

（2）当[a<0]时，由[f（x）=0]，得[x=1]或[x=ln（-2a）].

因此[f（x）]在[（1，+∞）]上单调递增.

当[x≤1]时， [f（x）<0]，

所以[f（x）]不可能有2个零点，不符合题意；

当[x∈（ln（-2a），+∞）]时， [f（x）>0]；

因此[f（x）]在[1，ln（-2a）]上单调递减，在[ln（-2a），+∞]上单调递增.

又当[x≤1]时， [f（x）<0]，

所以[f（x）]不可能有2个零点，不符合题意；

（3）当[a>0]时，[f（x）]在[（-∞，1）]上单调递减，在[（1，+∞）]上单调递增.

又因为[f（1）=-e<0]， [f（2）=a>0]，

所以[f（1）?f（b）<0]， [f（1）?f（2）<0]，

由零点存在性定理可知函数在[（-∞，1）]和[（1，+∞）]上均有1个零点，故[f（x）]存在2个零点.

综上可知，[a]的取值范围为[（0，+∞）].

解答本题，需利用导数与函数单调性之间的关系来判断出函数的单调性，进而根据函数的单调性讨论函数在区间上的取值，以便根据零点存在性定理判断零点的存在性.运用零点存在性定理解题，需确保函数在区间上的值有大于0的，同时也有小于0的，才能使零点左右两侧的函数值的积小于0.

二、数形结合

我们知道，函数的零点是函数与x轴交点的横坐标.因此在解题时，可根据题意画出函数的图象，讨论函数与x轴的交点的个数、位置，即可建立关系式，从而顺利求得问题的答案.有时函数可以拆分成[h（x）=g（x）-f（x）]的形式，那么[h（x）=g（x）-f（x）]的零点即为[g（x）]与[f（x）]的图象的交点，此时只需讨论两个函数图象的交点，就可以求出参数的范围.

例3.已知[fx]为偶函数，对[?x∈R]，有[fx+2=fx-f1]，当[x∈2，3]时，[fx=-2x2+12x-18].若函数[y=fx-logax+1]在[0，+∞]上至少有3个零点，则[a]的取值范围是（     ）.

解：令[x=-1]，由[fx+2=fx-f1]可得[f1=f-1-f1]，

而[fx]為偶函数，则[f1=f-1]，所以[f1=0]，

所以[fx+2=fx]，故[fx]是周期为2的函数.

令[fx-logax+1=0]，即[fx=logax+1]，

要使函数[y=fx-logax+1]在[0，+∞]上至少有3个零点，需使[fx]与[y=logax+1]至少有3个交点.

画出[fx]在[x∈2，3]的图象，并根据函数的周期性和对称性作出如图所示的图象，

由图象可知：当[a>1]时，[fx]与[y=logax+1]不可能有3个交点，

当[0f2=-2]，

总之，由函数零点的个数求参数的取值范围，不仅需要灵活运用导数、方程、不等式知识，还需运用分类讨论思想、数形结合思想、转化思想来辅助解题.