求解数列最值问题的三种途径
2023-03-31 05:48朱燕
语数外学习·高中版下旬 2023年12期
朱燕


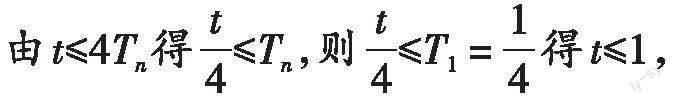
数列最值问题具有较强的综合性.这类问题侧重于考查对数列的定义、通项公式、性质、前n项和公式的应用.常见的数列最值问题有:(1)求数列的最大(小)项;(2)求数列的前n项和的最大(小)值.下面主要介绍三种求解数列最值问题的途径.
一、利用数列的单调性
数列是一种特殊的函数,其自变量为正整数,因此数列也具有单调性.通常可以将目标式看作关于n的函数式.在判断出函数的单调性后,即可利用函数的单调性来求解數列最值问题.也可以先根据数列的通项公式来判断出数列的单调性,再利用数列的单调性来求最值.
解:(1) an=3n-2;(过程略)
所以Tn+1>Tn,所以数列{Tn}是递增数列.
所以实数t的最大值是1.
一般地,若数列的前一项总比后一项小,则该数列为递增数列;若数列的前一项总比后一项大,则该数列为递减数列.由Tn+1>Tn,可判断出数列的单调性,即可根据数列的单调性得出Tn≥T1,从而求得t的最大值.
例2.在等差数列[an]中,[a1<0],[S9=S12],则数列[an]的前几项和最小?
解:因为[S9=S12],
解得[a1=-10d].
由于[a1<0],所以[d>0],
所以当[n=10]或[n=11]时,[Sn]的值最小,即数列[an]的前[10或11]项和最小.
二、运用放缩法
有些数列中的项有无限多个,我们很难快速求得数列的和,此时不妨运用放缩法,通过增减某些项、放大分母、缩小分子等方式,将数列的前n项和放大或缩小,即可顺利求得最值.
解答数列最值问题,往往需根据题目中所给的条件,仔细研究数列的特点、性质,将问题与数列、函数、不等式知识相关联,以快速找到解题的思路.
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
新世纪智能(数学备考)(2021年11期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
新世纪智能(数学备考)(2020年11期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27
河北理科教学研究(2020年1期)2020-07-24

