粗糙度各向异性对润滑接触面摩擦的影响*

张园园 李元庆，2 黄 培，2 付绍云，2

（1. 重庆大学航空航天学院 重庆 400044； 2. 输配电装备及系统安全与新技术国家重点实验室 重庆 400044）

机械零部件之间的摩擦行为往往伴随着能量的耗散， 使得一些关键零部件的传动效率以及疲劳性能降低[1］。 齿轮、 轴承、 凸轮等摩擦副是重要的机械基础件， 其润滑接触特性成为决定部件及装备性能与可靠性的关键因素[2］。 摩擦副之间适当的润滑状态一方面阻止两接触面的直接接触， 一方面起到冷却效果， 从而改善两接触体的摩擦行为。 深入理解继而控制、 优化摩擦副之间的摩擦行为， 能够有效控制机械零部件运行过程中的能量损失[3］， 降低接触面之间的磨损，延长摩擦副的服役寿命。

摩擦副之间的接触面并不是绝对光滑的， 接触面的表面粗糙度通常与润滑油膜的厚度具有相同数量级[4］， 对润滑接触面的摩擦行为有重要影响[5-10］。Stribeck 曲线（摩擦因数随“λ比” 变化的曲线） 可有效描述粗糙润滑接触面的摩擦行为[11］， 其中“λ比” 被定义为润滑油膜厚度与粗糙度初始幅值的比值。 早期的Stribeck 曲线主要是在轻载情况下通过试验的方式测得[12-14］， 其中粗糙度对摩擦因数的影响只与粗糙度初始幅值相关， 并未涉及粗糙度的形貌变化。 目前大多数关键机械零部件经常在高负载情况下运行， 单纯考虑粗糙度初始幅值对厘清粗糙度与摩擦因数的定量关系明显不足。

随着流体动力润滑理论的发展， 使得重载情况下的润滑粗糙接触行为数值分析成为可能[15］。 研究发现润滑条件下摩擦副的摩擦行为与多种因素有关。 例如圆锥滚子轴承挡边面与滚子端面椭圆接触的数值模拟研究发现， 接触面的弹性变形对摩擦因数的影响不可忽略[16］。 同时， 润滑剂的本构对接触面之间的摩擦行为也具有显著的影响[17-18］。 除了上述因素， 摩擦副接触面的粗糙度对于接触面间的摩擦行为也有重要影响， 接触面摩擦行为主要由油膜厚度与粗糙度参数决定。 油膜厚度作为主要影响因素之一， 与粗糙度幅值、 波长以及各向异性也息息相关[19-22］。 轻载（协调性接触） 情况下的润滑接触研究表明： 当“λ比” 等于3 时， 全膜润滑开始向混合润滑过渡[23］。最近基于数值模拟研究发现， 在重载（非协调性接触） 情况下， 接触面粗糙度会发生弹性形变， 其形变量依赖于工况条件以及粗糙度形貌[24-25］（该结果也被光弹实验验证[26］）。 这就意味着传统的参数“λ比” 已经不再适用于对重载情况下润滑接触面的摩擦因数变化情况进行描述， 亟需找到一个新的参数对重载下的润滑接触面的摩擦因数变化情况进行描述。

复杂的表面粗糙度可以分解成一系列正弦粗糙度分量叠加的形式， 本文作者基于瞬态弹性流体动力润滑理论， 构建正弦表面粗糙度， 并采用多重网格算法求解， 系统研究表面粗糙度各向异性对润滑接触面摩擦因数的影响， 并进行影响量化分析。 文中为解决表面粗糙度的引入造成控制方程的不连续性， 在多重网格算法中使用ALCOUFFE 等[27］构造连续插值算子的方式提高算法的稳健性。

1 数值模型

1.1 量纲一化方程

润滑接触问题首先需要推导待求解的控制方程组[28］， 考虑时变效应的量纲一化雷诺方程为

式中：P为量纲一压力；H为接触面间的量纲一油膜厚度为润滑油量纲一密度；T为量纲一时间；X为量纲一坐标， 其方向为接触面的相对运动方向；Y为垂直于相对运动方向的量纲一坐标。

量纲一化的具体过程参见文献[28］。 为简化雷诺方程， 使用了参数为润滑油的量纲一动力黏度； 变量其中为接触面1 和2 的平均线速度，η0为环境黏度，Rx为接触点的当量曲率半径，ah与ph分别为Hertz 接触半宽以及最大接触压力[28］，ah＝其中F是法向载荷，E′是等效弹性模量， 其定义为（1- v22）／E2。 同时雷诺方程的边界条件为

式中：Xa、Xb、Ya、Yb分别代表接触区域的边界。

在该模型中， 采用Dowson 和Higginson 的密度-压力方程[29］来描述润滑油的密度变化情况； 使用Roelands 的黏度-压力方程[30］来描述润滑油的黏度与压力的关系。

考虑表面粗糙度的量纲一油膜厚度方程为

式中： 指数项κ ＝10-10｛max[0，（X-X＾）／（λx／ah）］2｝用于加速数值计算程序的收敛， 其中为未变形粗糙度量纲一幅值，λx／ah与λy／ah分别为X和Y坐标方向的粗糙度量纲一波长。

与此同时， 采用参数r来表示粗糙度各向异性程度， 即：

当力平衡方程式（6） 满足时， 公式（3） 中的法向刚体位移H0即可确定。

在全膜润滑区域， 泊肃项与楔形项均对润滑剪切力有贡献， 对于牛顿流体， 当滑动速度适中时摩擦力主要由楔形项决定[31］， 即：

式中：S为滑滚比， 即滑动速度与卷吸速度之比。基于公式（7）， 相对摩擦因数可以定义为

式中： 下标rr 与ss 分别代表粗糙与光滑接触两种情况。

对于点接触问题， BOSMA 和MOES[32］为了进一步减少变量数目， 分别定义了2 个量纲一化参数来表征载荷、 速度与材料参数的影响， 即Moes 量纲一化参数M和L[32］：

式中：α为黏度-压力系数。

1.2 求解算法

对上述控制方程组进行离散。 量纲一化方程将在计算区域内的均匀网格上采用二阶近似的方式进行离散， 即： 泊肃项使用二阶中心差分格式， 楔形项与瞬态项使用二阶向前差分格式。 同时使用多重网格法来加快迭代收敛速度， 使用多重积分法（MLMI） 来计算弹性形变。 多重网格算法的实施可参考文献[28］。油膜厚度公式（3） 中的粗糙度项Ra波动剧烈， 使得传统的EHL 多重网格求解器不足以应对粗糙接触问题， 因此文中提出了基于Alcouffe 算法的粗网格构造方法来提高程序的稳健性。 Alcouffe 粗网格构造方法的具体实施过程见文献[33］。

接触模型量纲一化计算域选取为X∈[-2.5，1.5］ 和Y∈[-2.0， 2.0］ 的矩形区域， 同时最细网格上的节点数确定为513×513。 计算模型中的离散时间步长与空间域步长相同， 即0.007 812 5。 粗糙度设置的初始位置为X＝-2.5， 同时保证计算时间足够长使得计算结果展现出周期性。为了避免摩擦因数比的分母出现0 的情况， 使用一个较小的滑滚比S＝0.02。 该模型数值求解的过程如图1 所示。

图1 TEHL 模型数值求解流程Fig.1 Flow of the numerical simulation process for the TEHL model

2 计算结果与讨论

为讨论表面粗糙度各向异性对相对摩擦因数的影响规律， 分别研究纵向粗糙度（λx ＞λy）， 横向粗糙度（λy ＞λx） 以及纯纵向粗糙度（λx ＝∞） 对摩擦副接触面摩擦行为的影响。 所需数值模拟参数如表1 所示。

表1 数值模型参数Table 1 Parameters for the numerical model

2.1 数值求解

表2 所示为载荷在M ＝1 000 与L ＝10 的情况下，表面粗糙度波长分别为λx／ah＝1，λy／ah＝0.5， 中心油膜厚度与粗糙度初始幅值之比为3， 即Hc／Ai＝3时， 经过30 个“V” 循环后， 不同网格节点数下，经典多重网格算法[28］与Alcouffe 粗网格算子实施后的算法， 其计算误差的对比。 可以看出， 改进算法的计算精度在各个网格节点情况下都要比传统算法高， 即雷诺方程与力平衡方程的残差均比传统算法小3 ～4个数量级。 尤其当网格节点数为1 025×1 025 时， 经典多重网格算法不收敛， 改进后的算法依旧给出了较高的计算精度。 因此， 使用Alcouffe 方法改进后的多重网格算法在求解粗糙表面接触问题时具有更高的稳健性。

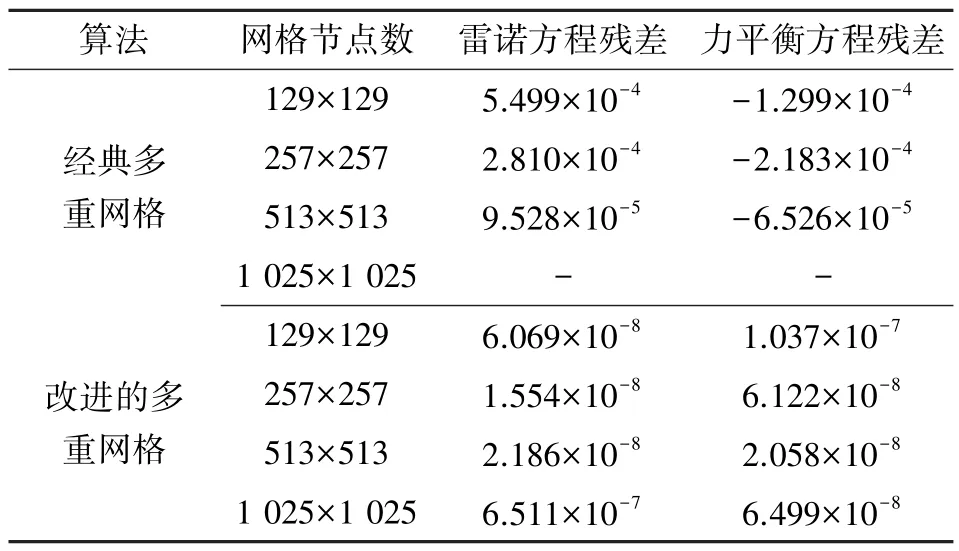
表2 经典多重网格算法与实施Alcouffe 粗网格构造法的多重网格算法计算误差对比Table 2 Comparison of calculation errors between the classical multilevel method and multilevel method implementing Alcouffe’s coarse grid construction

网格密度的选取与数值解的精度以及计算时间息息相关， 网格密度过大， 计算精度不够， 将导致计算结果失真； 网格密度过小， 计算时间长， 计算代价太大。 表3 所示为相对摩擦因数与网格节点数的关系，结果表明当计算区域内的节点数设置为513×513 时，具有优于1%的计算精度以及较小的计算代价， 因此文中的网格节点数选择为513×513。

表3 网格节点数对相对摩擦因数的影响Table 3 Effects of the mesh point on the relative friction coefficient

将文中数值模型计算结果与文献[24］拟合的计算结果进行对比来验证数值模型的正确性。 图2 所示为文中求解的粗糙度相对幅值变化与文献[24］中拟合出的粗糙度幅值变形公式的对比， 结果显示文中数值模型计算的结果全部落在了文献拟合的主曲线上，说明提出的数值模型能够有效用于润滑粗糙接触面的摩擦行为分析。

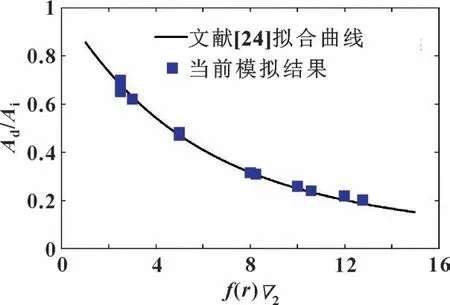
图2 粗糙度幅值变化与f（r）的关系：当前模型与文献[24］结果对比Fig.2 The relative deformed amplitude as a function of f（r）： results comparison of the current model with those of Ref. [24］

2.2 瞬时解

图3 所示为摩擦副接触面表面粗糙度分别表现出各向同性 （λx／ah＝λy／ah＝0.5）、 纵向 （λx／ah＝1，λy／ah＝0.5）、 横向（λx／ah＝0.5，λy／ah＝1） 时， 相同载荷（M ＝1 000，L ＝10 和Hc／Ai＝2） 下的压力、油膜厚度分布与相对摩擦因数随时间的变化情况。 图3 左图显示由于接触面形貌发生了改变， 对应的油膜厚度分布发生变化， 此时压力分布也发生变化。 根据公式（7）， 润滑状态下的摩擦力与油膜厚度和黏度相关， 因此接触面形貌变化会引起接触面摩擦行为的改变。 同时从油膜厚度的干涉图中可以看出， 粗糙度形貌各向异性也会影响油膜厚度的分布， 因此可以推断接触面摩擦与粗糙度形貌各向异性也相关。 由于接触面粗糙度为周期性函数， 相对摩擦因数也具有周期性， 如公式（8） 显示相对摩擦因数是时间依赖参数。 因此在以下的研究中， 使用相对摩擦因数在一个完整周期内的平均值作为其在指定工况下的数值， 即从图3 中可以看出， 尽管载荷、 速度、初始粗糙度幅值以及波长都一致， 但是对于不同的r， 相对摩擦因数变化， 即： 当r＝1 时μR＝1.790； 当r＝2 时μR＝1.566； 当r＝0.5 时μR＝1.484。 该结果直接表明粗糙度表面各向异性特性影响润滑情况下接触面的摩擦情况。 下文将会进一步探讨粗糙度表面的各向异性程度对接触面摩擦因数的影响情况。

图3 3 种粗糙度各向异性情况下的粗糙度形貌、压力分布、 油膜厚度分布（左图） 与相对摩擦因数随时间的变化情况（右图）Fig.3 Surface roughness topographies， pressure distributions， film thickness distributions （left） and relative friction coefficient as a function of the time （right） for three different roughness anisotropy conditions： （a） isotropic case；（b） longitudinal case； （c） transverse case

2.3 纵向和横向表面粗糙度的影响

图3 表明相同工况下， 不同的表面粗糙度各向异性参数r造成不同的相对摩擦因数， 因此， 文中研究了表面粗糙度各向异性对接触面摩擦因数的影响， 并将该影响量化。 为了简便起见， 以下的研究采用相同的载荷、 速度、 粗糙度y方向的波长等工况参数， 即M＝1 000，L＝10 以及λy／ah＝0.5。 图4 所示为不同纵向表面粗糙度（参数r ＞1） 下相对摩擦因数随“λ比”， 即Hc／Ai的变化情况。

从图4 可以看出， 各向异性表面粗糙度情况下的摩擦因数曲线与各向同性表面粗糙度情况下的曲线具有相同的变化趋势， 即随着Hc／Ai的增大， 摩擦因数逐渐减小。 这是因为随着Hc／Ai的逐渐增大， 接触面粗糙度波动逐渐减小， 接触面逐渐趋于“光滑”， 因此相对摩擦因数趋于1。 对于每个粗糙度各向异性参数r， 对应着一条光滑的摩擦因数曲线， 所有的曲线均分布在各向同性r ＝1 曲线的左侧。 从图4 放大的右图中可以看出，r＝16 与r＝32 的曲线基本重合，这就说明曲线的左移是有限的。 这些情况与AR（Amplitude Reduction） 理论[24］里的情况相似， 因此如果找到一个和AR 理论相似的函数将所有的接触面表面粗糙度各向异性对摩擦因数曲线的影响统一， 即可以得到一条统一的相对摩擦因数曲线。 利用纵向表面粗糙度情况下摩擦因数曲线的右移， 得到了公式（10）， 从而使得摩擦曲线统一为如图5 所示。

图4 不同粗糙度各向异性情况（1≤r≤32） 下相对摩擦因数μR 随Hc／Ai 的变化情况（左图）， Hc／Ai∈[2.3， 2.7］ 时的相对摩擦因数放大情况（右图）Fig.4 Relative friction coefficient as a function of Hc／Ai for different r （1≤r≤32） values （left），zoom from 2.3 to 2.7 （right）

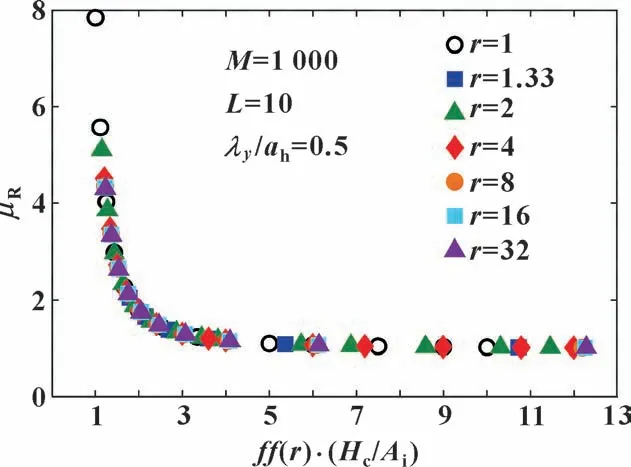
图5 纵向表面粗糙度情况下的统一相对摩擦因数曲线：相对摩擦因数μR 随ff（r）·（Hc／Ai） 的变化情况Fig.5 The unified friction curve for longitudinal surface roughness cases： μR as a function of ff（r）·（Hc／Ai）

采用相同的载荷、 速度、 表面粗糙度x方向的波长等工况参数， 即M＝1 000，L＝10 以及λx／ah＝0.5来研究横向表面粗糙度对摩擦因数的影响。 图6 所示为不同横向表面粗糙度（参数r ＜1） 下， 相对摩擦因数随“λ比”， 即Hc／Ai的变化情况。 与纵向表面粗糙度情况相比， 横向表面粗糙度情况较复杂。 从图6 中可以看出， 摩擦因数曲线分布在各向同性r ＝1 曲线的两侧， 当参数r从0 变化到0.33 时， 相对摩擦因数逐渐减小（虚线）； 当参数r从0.4 变化到1 时，相对摩擦因数逐渐增大（实线）。

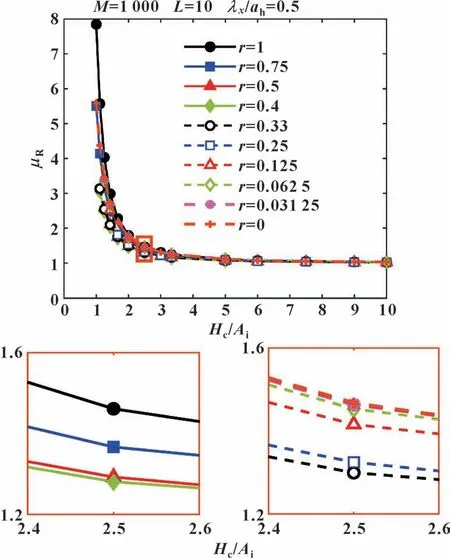
图6 不同粗糙度各向异性情况（0≤r≤1） 下相对摩擦因数μR 随Hc／Ai 的变化情况（上图）， Hc／Ai∈[2.4， 2.6］时的相对摩擦因数放大情况（下图）Fig.6 μR as a function of Hc／Ai for different r （0≤r≤1）values （upper）， zoom from 2.4 to 2.6 （lower）

与纵向表面粗糙度情况相似， 提出一个描述表面粗糙度各向异性程度的放缩函数， 可以将所有横向表面粗糙度情况下相对摩擦因数曲线统一成单一曲线（如图7 所示）， 该函数为

图7 横向表面粗糙度情况下的统一相对摩擦因数曲线：相对摩擦因数μR 随ff（r）·（Hc／Ai） 的变化情况Fig.7 The unified friction curve for transverse surface roughness cases： μR as a function of ff（r）·（Hc／Ai）

前期研究工作[31］表明， 相对摩擦因数与工况参数相关， 针对各向同性接触面表面粗糙度情况， 得出了一个放缩系数θ2， 在较大的工况范围内（500≤M≤2 000， 5≤L≤15 以及0.25≤λ／ah≤1.0） 将所有的摩擦因数曲线组织成了一条单一曲线。 进一步将各向同性与各向异性粗糙度情况结合， 可得到如公式（12） 所示的统一方程， 其中粗糙度各向异性特性可使用分段函数（见式（13） ） （如图8 （a） 所示）来描述。 最后在较大工况范围内将所有的相对摩擦因数统一成一条单一曲线， 得到非协调性表面摩擦副润滑粗糙接触情况下的Stribeck 曲线， 如图8 （b）所示。

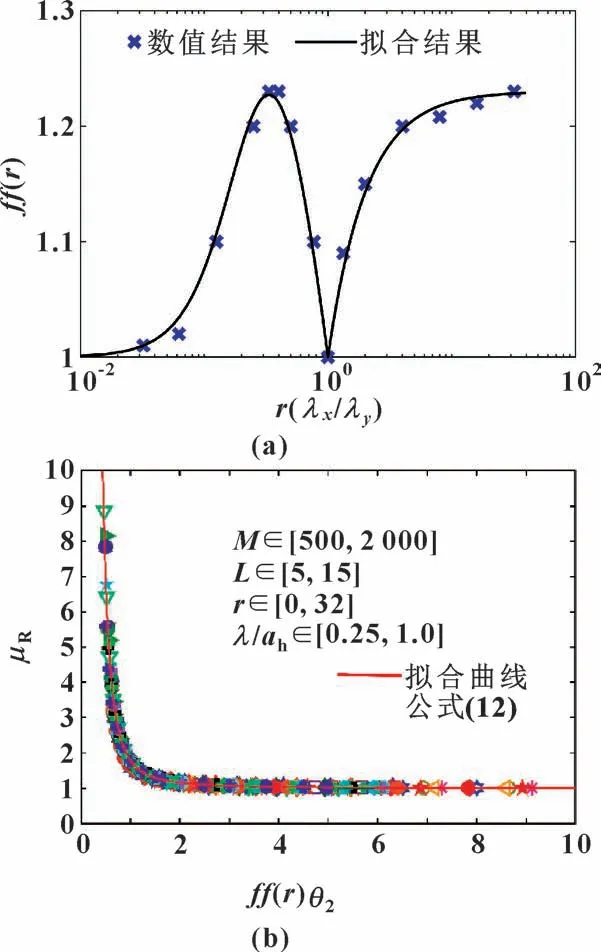
图8 描述粗糙度各向异性特性的函数ff（r） 随r 的变化情况（a）， 高负载非协调性接触下的Stribeck 曲线（b）Fig.8 ff（r） as a function of r（a）， the Stribeck curve for the highly loaded non-conformal contacts （b）

2.4 纯纵向表面粗糙度的影响

研究发现[34］， 瞬态纯纵向表面粗糙度情况下的润滑接触情况与稳态纯纵向表面粗糙度情况下的结果相同。 当工况为M＝1 000，L＝10，Hc／Ai＝2，λy／ah＝0.5 以及λx＝∞时瞬态纯纵向表面粗糙度情况下， 相对摩擦因数与稳态结果的对比如图9 所示。 正如文献[34］所述， 除去磨合阶段， 瞬态的结果和稳态的结果确实相同。 上述研究发现， 摩擦因数的变化主要是由粗糙度（公式（4） ） 的变化引起的， 当λx＝∞时，公式（4） 中横向粗糙度项消失， 表面粗糙度项将变成非时间依赖项， 即此时雷诺方程中的瞬态项关于油膜厚度的一阶偏导也消失， 即瞬态雷诺方程退化成稳态雷诺方程。

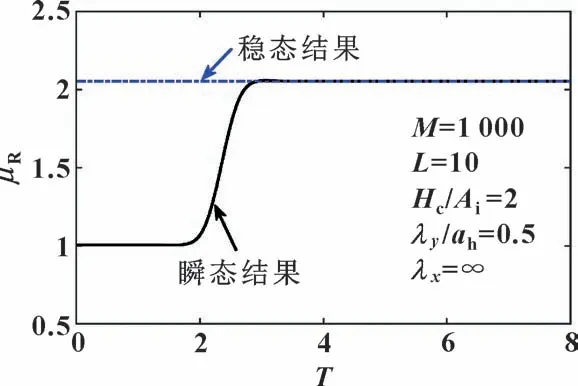
图9 瞬态纯纵向表面粗糙度情况下相对摩擦因数与稳态结果的对比情况Fig.9 Comparison between the transient relative friction coefficient and that of the stationary case

表4 所示为纵向各向异性粗糙度与纯纵向各向异性粗糙度对相对摩擦因数的影响。 数据显示， 随着表面粗糙度各向异性参数r从1 增长到32， 相对摩擦因数逐渐减小， 然而纯纵向各向异性粗糙度情况具有最高的摩擦因数， 情况与2.3 小节的结果不同。 因此有必要将该情况单独分析。

表4 相对摩擦因数随纵向表面粗糙度各向异性程度的变化Table 4 Relative friction coefficient versus different surface roughness orientations

图10 所示为纯纵向表面粗糙度下， 相对摩擦因数的变化情况（工况范围：M∈[500， 2 000］，L∈[5， 15］ 与λy／ah∈[0.25， 0.8］ ）。 从图10 （a）中可以看出， 对于每组工况， 都存在一条光滑的相对摩擦因数曲线。 由于文献[31］提出的参数θ2已经不能统一纯纵向表面粗糙度情况下的摩擦曲线， 提出了一个新的单独参数（表达式见公式（14） ） 将所有纯纵向表面粗糙度情况下的摩擦因数曲线簇整合成一条单一曲线， 如图10 （b） 所示。

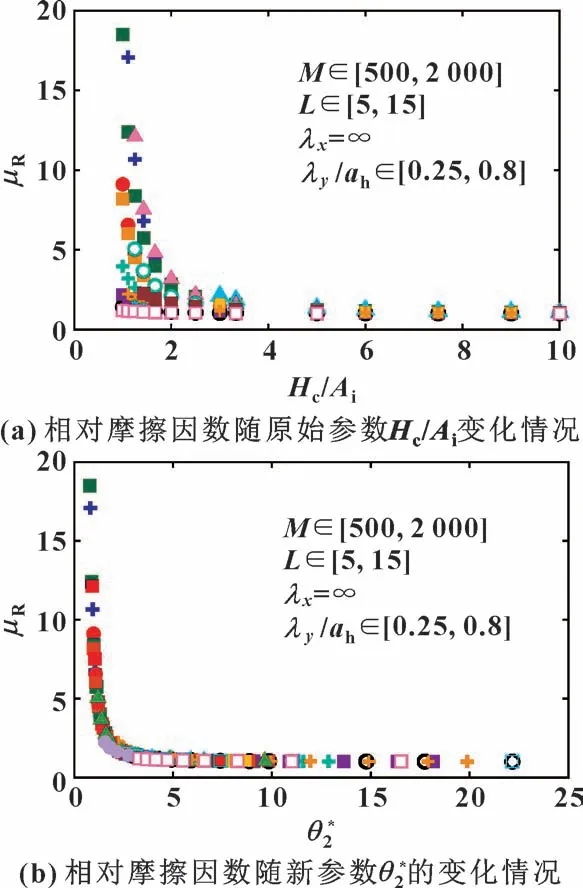
图10 纯纵向表面粗糙度情况下的相对摩擦因数Fig.10 Relative friction coefficient for the purely longitudinal wavy case： （a） μR as a function of the original parameter Hc／Ai； （b） μR as a function of the new parameter

3 结论

（1） 在非协调性表面接触情况下， 润滑接触面粗糙度的各向异性对粗糙度形变量影响显著， 使得接触面压力分布、 油膜厚度以及润滑油黏度发生变化，进而导致摩擦因数发生变化。

（2） 接触面粗糙度各向异性的程度影响润滑状态的摩擦因数， 该影响可以通过一个函数ff（r） 量化， 表明全膜润滑到混合润滑的过渡不仅与载荷、 速度等工况参数相关， 还与粗糙度各向异性相关。

（3） 纯纵向粗糙度情况下， 瞬态效应消失使得润滑模型转变为稳态模型， 参数θ2不能描绘纯纵向表面粗糙度情况， 拟合得到一个单独的放缩系数实现纯纵向粗糙度情况下摩擦曲线簇的统一。