基于虚拟制备的大环径比O 形金属橡胶密封件结构性能研究*
任志英 吴丁丁 史林炜 张兆想 谭桂斌 黄 兴,3
(1. 福州大学机械工程及自动化学院, 金属橡胶与振动噪声研究所 福建福州 350116;2. 广东工业大学省部共建精密电子制造技术与装备国家重点实验室 广东广州 510006;3. 国家橡塑密封工程技术研究中心 广东广州 510535)
密封技术是工程应用领域影响设备安全的关键技术, 随着科技的发展, 某些设备必须适应太空、 深海、 极地等极端环境, 而传统的橡胶密封材料在本质属性上有一定的局限性, 其在高温易老化、 低温易脆裂, 无法满足日益复杂的工程需求[1-3]。 传统橡胶密封圈如图1 (a) 所示。 因此, 研发特殊工况下的高性能密封件, 一直是密封防泄漏领域的重要研究课题之一[4-5]。 金属橡胶作为一种大变形材料, 具有工作温度范围大、 抗腐蚀、 强度高等特性, 可以适应恶劣的工程环境, 在密封领域的应用越来越多[6-7]。 由于金属橡胶在外载的作用下可以实现压缩、 回弹及阻尼耗能等作用[8], 因此在特殊工程应用环境中可以通过外加C 形、 矩形、 O 形等的金属外壳或橡胶类包裹层, 实现密封的功能。 金属橡胶密封圈如图1 (b)所示。

图1 橡胶和金属橡胶密封圈Fig.1 Rubber (a) and metal rubber (b) seals
目前国内外研究人员已经对金属橡胶密封做了大量的研究。 姚伟[9]研究了金属橡胶静密封系统失效的原因, 通过试验与有限元仿真分析得到密封件的可靠度函数, 并通过该函数对金属橡胶密封件的工作寿命进行了预测。 王亮[10]研究了不同相对密度的金属橡胶试样的应力及应变之间的关系, 阐述了金属橡胶材料的弹性模量、 泊松比等力学性能参数, 并针对某一种相对密度推导了弹性模量与泊松比的计算关系式,建立了金属橡胶密封系统的简化力学模型, 进一步推导了理论计算模型。 姜旸和索双富[11]研究了针对W形金属密封环综合性能优化的方法, 并从稳定性、 密封性和回弹性三方面分析和验证了优化方法的可行性。 袁涛[12]研究了金属橡胶气密封的泄漏率, 基于Navier-Stokes 方程和Persson 的接触理论[13]推导出了泄漏率计算公式, 并搭建试验台进行了验证。 MA等[14]采用简化三维指环模型, 分析了结构参数对弹簧自紧式密封圈的压缩回弹性的影响, 为开口复合型密封件的仿真提供了新思路。 李玉龙等[15]提出了特大型柔性密封环结构设计的初步方案, 并对以金属橡胶为骨架、 橡胶为外包覆层设计的密封环结构进行静力学有限元仿真, 验证了该方案满足实际工况要求。
综上, 学者们围绕MRS 这类复合密封件的制备工艺、 结构设计及仿真分析等已做了大量的研究, 但由于MRS 结构的复杂与工艺的繁琐, 目前的研究主要集中在小尺寸密封件的研制。 而对于一些大环径比, 即截面尺寸很小但整体直径很大的耐高温密封件的研究较少。 此外, 在建立MRS 有限元模型时, 目前多是将MR 弹性内芯简化为一种连续、 均质且各向同性的材料[16], 因而模型无法反映出MR 内部无序勾连的复杂结构[17]的力学性能。 因此, 本文作者针对大环径比O 形金属橡胶密封件的研制需求, 研究其制备工艺, 并通过试验分析金属橡胶密封件的静力学性能; 同时基于虚拟制备技术构建能反映出金属橡胶密封件真实拓扑结构的微段数值模型, 探究各因素对金属橡胶密封件综合性能的影响规律, 并对该类型密封件的性能进行预测, 对工程应用有一定的理论指导价值。
1 大环径比金属橡胶密封件制备工艺
金属橡胶材料由于其多孔性, 无法直接用于密封和防泄漏, 常采用增加开口包覆层来实现密封功能。因此, MRS 制备流程分为2 个模块: 一是MRS 内芯(即金属橡胶) 的制备; 二是MRS 包裹层的制备,以及其与弹性内芯组装制作, 制备流程见图2。 文中以大环径比O 形MRS 的需求作为技术背景, 其尺寸参数如下: 内径276 mm, 外径283 mm, 截面直径3.5 mm。

图2 金属橡胶密封件制备流程Fig.2 Preparation process of metal rubber seals
其中金属橡胶的制备流程一般分为3 个阶段。(a) 前处理阶段: 选取一定材质丝材并卷制成线匝。选取304 不锈钢丝为原材料, 丝径为0.20 mm。 前处理得到的金属螺旋卷材料参数如表1 所示。 (b) 毛坯成型阶段: 以一定规则使用缠绕工艺制成金属橡胶毛坯。 缠绕毛坯工艺参数如表2 所示。 (c) 冷压成型及后处理阶段: 利用冷冲压成型技术在限定压力下冲压成型, 并进行一系列的热处理[20]。 文中设计了一套大环径比O 形金属橡胶弹性内芯专用压制成型模具, 如图3 所示, 相关参数见表3。 该模具满足了大环径比MR 从冲压至退模的要求。

表1 螺旋卷材料参数Table 1 Material parameters of spiral coil
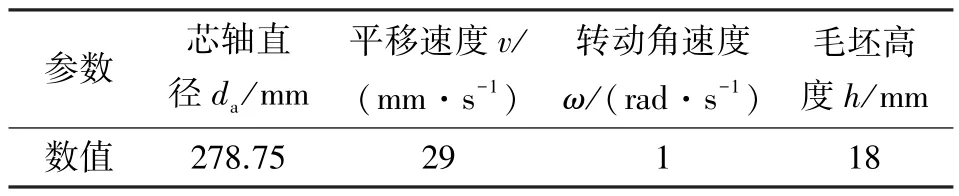
表2 毛坯工艺参数Table 2 Blank process parameters
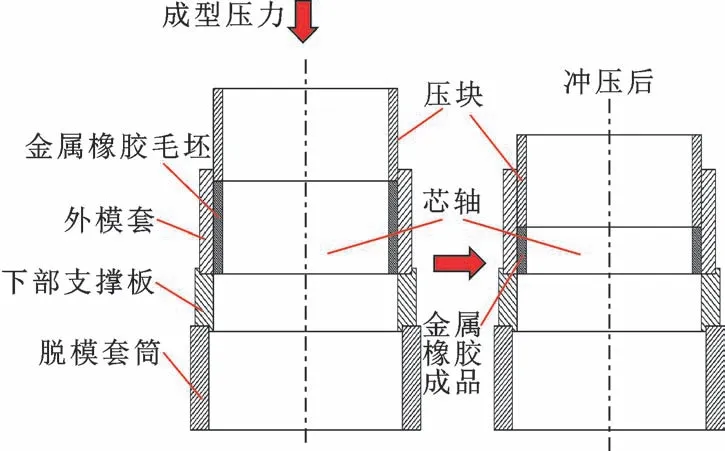
图3 金属橡胶冲压模具示意Fig.3 Schematic of metal rubber stamping die
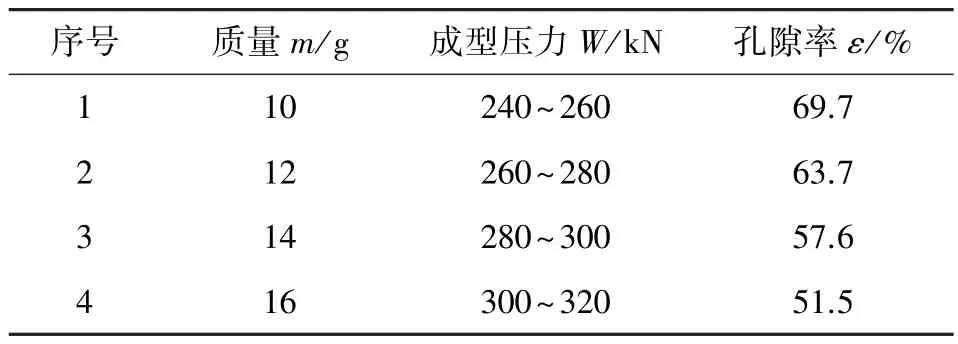
表3 MR 冲压参数Table 3 MR stamping parameters
制备成型的金属橡胶弹性内芯因为缺少成型模具的约束, 会出现微量扩张。 因此为了将金属橡胶弹性内芯放置在不锈钢毛细钢管包裹层中, 采用了铣床切割机进行精确切取毛细不锈钢管, 开槽宽度为(2±0.1) mm。 然后, 将开槽的钢管放置在特制的折弯模具中进行折弯、 整圆工艺处理。 包覆层材料参数如表4 所示。
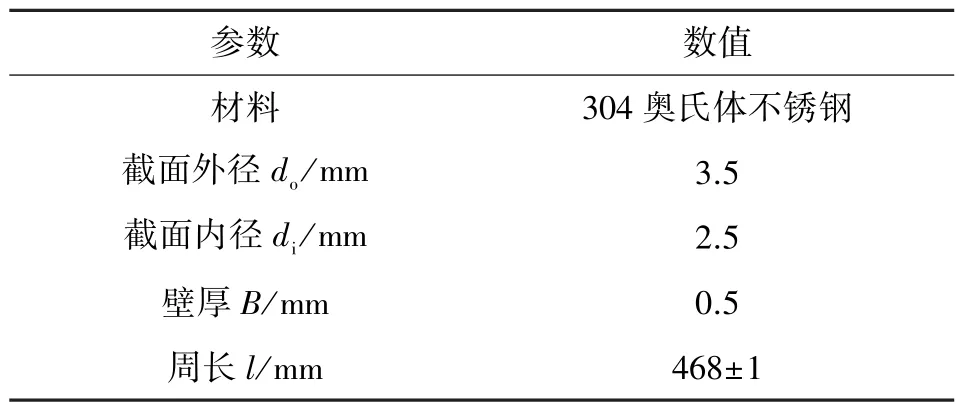
表4 包覆层材料参数Table 4 Cladding material parameters
2 金属橡胶密封件静力学性能分析
从上述制备过程可看出, MR 内芯的制备过程非常复杂, 且文中制备的MRS 环径比较大。 为了说明文中所制备产品的一致性, 通过对金属橡胶内芯力学性能的稳定性分析和MRS 几何尺寸偏差的测量进行了验证和解释。
为了对金属橡胶内芯力学性能进行稳定性分析,在电子万能材料试验机上进行金属橡胶试样的测试。从制备的4 种不同孔隙率MR 内芯中(见表3), 选取同批次的3 个样品进行径向截面准静态压缩试验,得到的力-位移曲线如图4 所示。 由于内芯主要在密封系统提供支撑力, 文中用等效刚度来描述每组试件的性能稳定性。 如图4 所示, 若记忆体-位移曲线为L(x), 则等效刚度由下式计算:
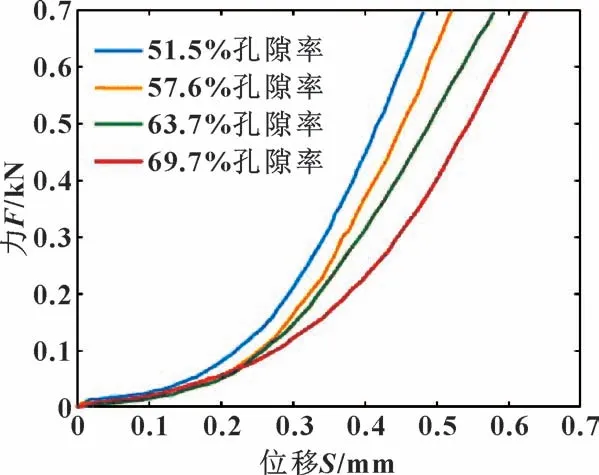
图4 金属橡胶内芯力-位移曲线Fig.4 Force-displacement curves of MR inner core
式中: dx为相邻两个计数点间的位移差;N为计数点。
在评估MRS 几何尺寸偏差程度时, 整体MRS 的平面翘曲是应考虑的主要因素, 因为大的环径比使其在最后焊接合拢阶段易变形翘曲。 如图5 (a) 所示,将MRS 与两块限位板固定, 通过射线投影法测量限位板之间的距离, 最终得到6 个同批MRS 试件的平面翘曲值, 如图5 (b) 所示。
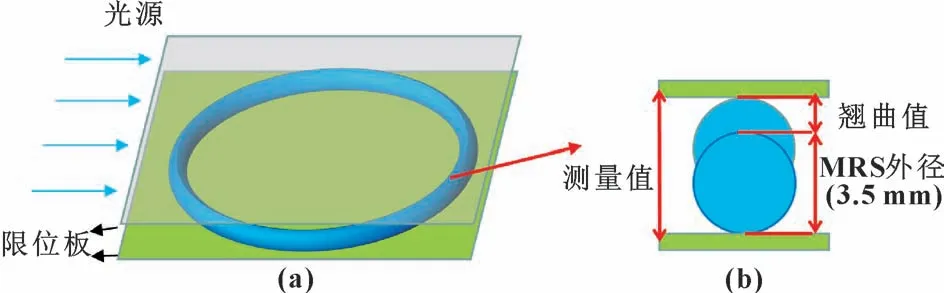
图5 MRS 翘曲测量法Fig.5 MRS warpage measurement method
测量所得数据如表5、 表6 所示。 由表5 可看出,相同参数下制备的金属橡胶试样一致性较好, 每组试样之间的最大相对误差为8.75%, 表明MR 制备工艺稳定可靠。 表6 给出了同批制备的6 个MRS 试件样品的翘曲值。 可以看出, 每一类试样都有一定程度的翘曲, 这是由于包覆层激光焊接产生的应力导致整体翘曲; 同时, 较大的环径比使翘曲值增大, 平均观测值为3.57 mm。 但试样翘曲值的均方差仅为0.08 mm, 也说明了包覆层制备过程的稳定性。
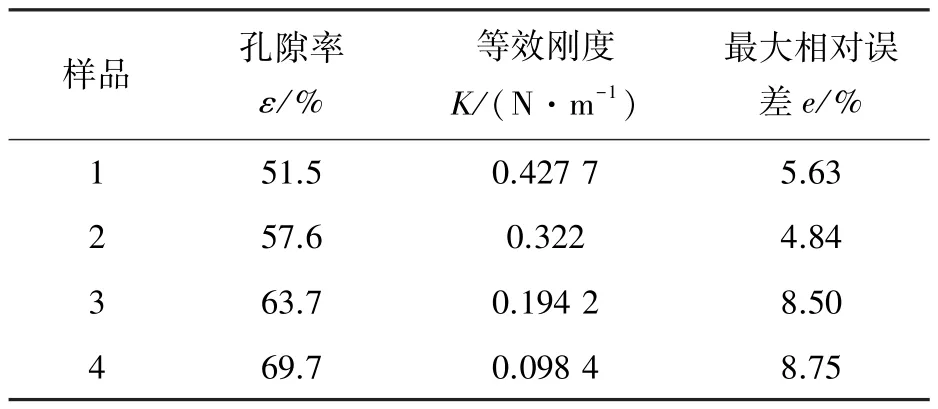
表5 MR 等效刚度误差Table 5 MR equivalent stiffness error
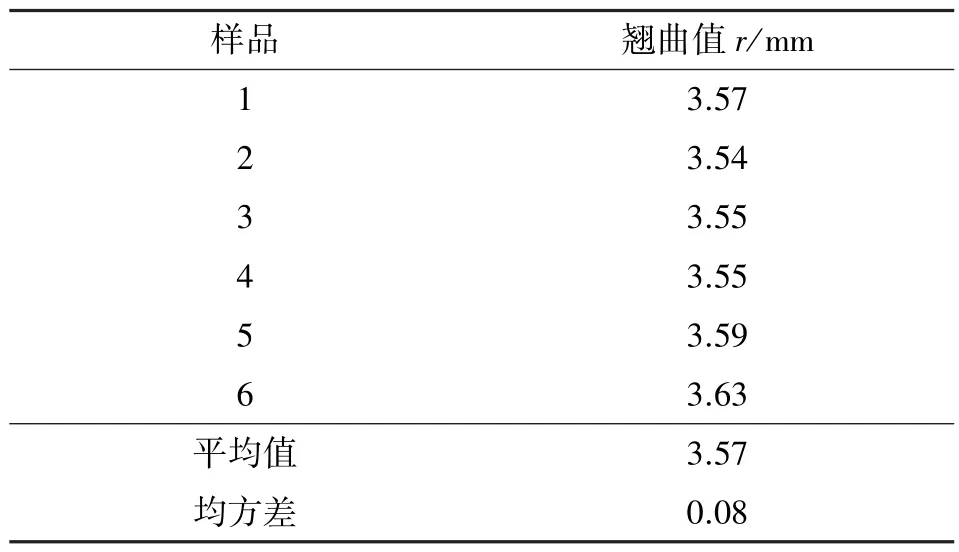
表6 MRS 翘曲值Table 6 Warpage of MRS
3 MRS 模型建立及密封特性分析
接触特性是评估金属橡胶密封件性能的重要指标, 密封界面之间的接触应力大于密封介质压力是金属橡胶密封件不发生失效的必要条件。 密封件包覆层和MR 弹性内芯的材料性能及其工作过程中发生的接触变形, 与金属橡胶密封件的力学性能密切相关。 传统实验手段及有限元分析方法无法完全反映出MRS的真实几何拓扑结构及接触特性, 因此, 文中基于MR 虚拟制备技术, 依据实际制备工艺建立了MRS真实几何模型及其压缩工况仿真模型, 通过仿真方法分析了金属橡胶密封件压缩工况对接触特性的影响。此外, 为了研究MRS 密封系统的泄漏率, 还对MRS密封件进行了流体仿真分析。
3.1 MRS 几何模型及密封工况模型建立
MR 虚拟制备技术, 是依据MR 特殊的制备工艺, 完成从丝材参数选取到冷压成型的全过程虚拟仿真, 其过程中所用的参数具有充分的物理意义且获得的几何模型高度反映了MR 的真实结构特征[18-19]。
通过螺旋卷不断自转的同时, 其局部坐标系也沿着旋转轴线旋转使其不断更新迭代, 从而得到单根金属橡胶螺旋卷的全局坐标参数。 然后, 通过模拟自动化缠绕机的绕制过程, 得到金属橡胶螺旋卷绕制后的毛坯。 最后, 引入罚函数算法[20-21]完成了从金属橡胶毛坯制备到冲压成型的制备流程。 制备流程及虚拟样品和实物结构比较如图6 所示。 可以看到MRS 虚拟样品线匝细观纹理与实物材料呈现出高度的一致性。

图6 MRS 虚拟制备流程及虚拟样品和实物结构比较Fig.6 MRS virtual fabrication process and comparison of virtual sample and physical structure
金属橡胶密封系统一般由上法兰盘、 下法兰盘、金属橡胶密封件以及螺栓紧固件组成。 金属橡胶密封件主要依靠螺栓载荷作用下所产生的变形在密封界面间形成一定的接触应力来保证密封不发生失效, MRS密封系统模型如图7 所示。 为模拟真实工况及简化计算, 所设的约束条件及假设如下: (a) 由于法兰盘材料刚度远大于MRS, 为简化计算, 将上下工作表面及侧壁设为刚性壳单元; (b) 包覆层端面和金属橡胶内芯端口处沿周向方向为对称约束, 且认为MR内芯在模型段内分布不均匀, 但能反映整体MR 特征, 即整体均匀; (c) 上工作表面只释放Z向自由度; (d) 下工作表面和侧壁完全固定。
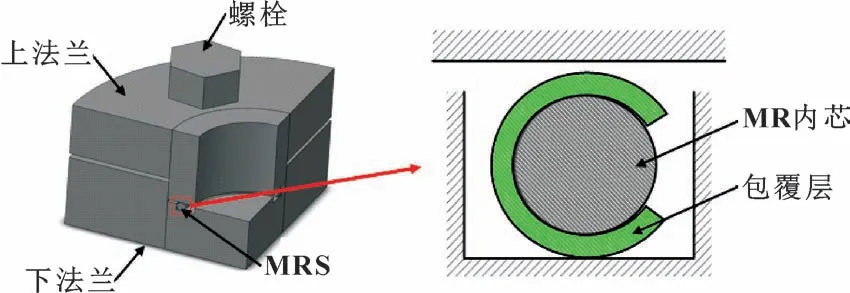
图7 MRS 密封系统模型Fig.7 MRS sealing system model
3.2 MRS 压缩工况结构特性分析
为了解压缩率对于MRS 结构特性的影响, 对MR内芯孔隙率为63.7%的密封件开展压缩率为10%、15%、 20%的仿真计算, 得到MRS 在各个工况及孔隙率下的位移分布、 von Mises 应力分布及等效塑性变形分布, 以探究MRS 复合密封件在轴向压缩工况的力学特性。 由于金属橡胶的应力应变关系可以等效为小曲梁或悬臂梁, 因此仿真模型中的金属橡胶采用梁单元来表示。 图8 所示为63.7%孔隙率的MRS 在10%压缩工况下的结构响应结果。
由图8 (a) 可以看出, 在压缩工况下, MRS 的最大位移位于包覆层开口上端处; 另外包覆层外表面整体位移大于内表面, 且在与固定的下表面接触的区域位移也不为0, 这种现象产生的原因是开口处没有力的支撑, 导致包覆层截面在压缩过程中有绕周向的整体转动。 而对于von Mises 应力来说, 如图8 (c)所示, 包覆层在左侧内壁处有较为明显的应力集中现象, 故该处出现断裂和失效的可能性最大; 另外总体来看, 应力分布并不均匀, 这是由于MR 弹性内芯是一种多孔材料, 在所截取的微段内也不是完全的均匀分布, 所以不能当作一种均匀连续的材料。 如图8 (d)所示, MR 弹性内芯在压缩过程中所产生的von Mises 应力也呈不均匀分布状态。 而对于塑性变形来说, 如图8 (b) 所示, 产生塑性变形的主要位置与von Mises 应力集中的区域相同, 即在压缩工况下包覆层左侧处具有较大的塑性变形。
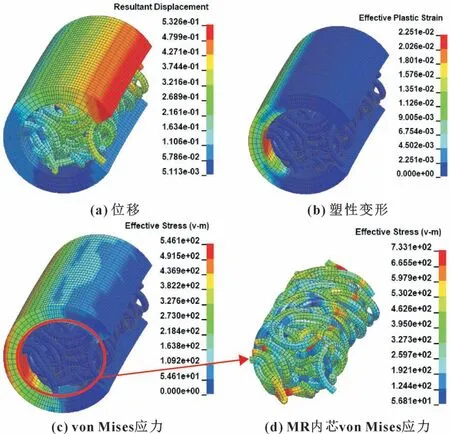
图8 10%压缩率下63.7%孔隙率MRS 结构的仿真结果Fig.8 Simulation results of MRS structure with 63.7% porosity under 10% compression: (a) displacement;(b) plastic strain; (c) von Mises stress;(d) von Mises stress of MR inner core
对于密封系统宏观模型所产生的压缩变形, 可通过仿真计算相应服役工况下密封界面间的接触应力分布来了解。 对于金属橡胶密封系统, 密封界面有两处, 分别为密封件与上下法兰盘的接触变形区域, 由图8 (a) 可知密封件与上下法兰盘接触区域的变形并不呈对称分布, 这可能会导致两处接触应力分布情况并不一致。 图9 所示为63.7%孔隙率的MRS 在10%、 15%及20%压缩率下MRS 上下表面及包覆层内表面接触压力云图。
如图9 所示, 压缩工况下MRS 上下表面接触压力分布并不一致, 且在各自区域内分布并不均匀, 这主要是因为MR 弹性内芯提供的支撑力并不均匀, 其提供的支撑力在某一时刻呈现多区域分布的集中力形式。 如图9 所示, 随着压缩率的增大, MRS 上下表面接触压力增加, 且上表面接触区域的中心发生了较大的径向移动, 这是由于开口处缺少对称支撑, 导致MRS 上表面接触区域随着压缩率增加发生了较大径向位移, 而下表面区域径向位移较小, 这与图8 (a)中结果相符。 此外, 对比不同压缩率时上下表面的接触压力峰值可知, 在压缩率为10%时, 上表面接触压力峰值略大于下表面, 在压缩率为15%时, 上下表面接触压力峰值差增大, 而在压缩率为20%时,上表面接触压力峰值差进一步增大。 这一现象可从不同压缩率下包覆层的形貌关系及塑性变形来解释。 在压缩率较小时, 包覆层外层与上下工作表面接触区域的曲率变化并不大, 且由于上接触区域发生位移, 已经发生塑性变形的弹性区域不断与上表面接触, 因此在10%压缩率下, 上接触区域压力峰值要大于下接触区域, 但由于下接触区域产生的塑性变形不大, 故差异不明显。 而随着压缩率的增大, 由于包覆层上表面存在绕周向的整体转动, 使得上接触区域的接触面积不断减小, 同时下接触区域塑性变形的增加使得上接触区域与下接触区域的接触压力峰值差不断增大。对比文献[4]中相同工况下的仿真结果, 可验证上述仿真结果的有效性。 总之, 对于该型密封件而言, 应使上下接触压力尽量接近, 从而达到最好的密封性能。
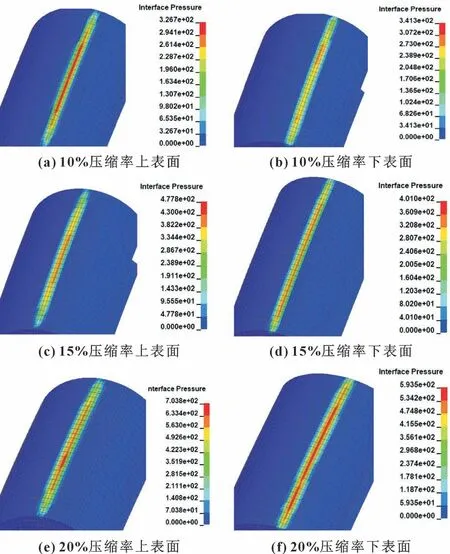
图9 63.7%孔隙率MRS 不同压缩率时上下表面接触压力云图Fig.9 Contact pressure nephogram on upper and lower surfaces of MRS with 63.7% porosity under different compression:(a) upper surface under 10% compression; (b) lower surface under 10% compression; (c) upper surface under 15% compression; (d) lower surface under 15% compression;(e) upper surface under 20% compression;(f) lower surface under 20% compression
3.3 MRS 密封系统流场及泄漏率分析
泄漏率是衡量密封件密封性能的重要指标, 表示泄漏率大小最直观的方法之一是泄漏通道的几何尺寸。 但实际泄漏通道不仅微小, 而且截面积大小、 长短、 截面形状极不规则, 因此难以通过最直观的方法来表示泄漏率的大小, 而是通过单位时间内泄漏介质的体积或质量来表征。 文中研究的密封属于静密封,且泄漏间隙较小, 因此流体在间隙中的流动可看作稳态层流流动。 密封件被压缩后的间隙流动模型如图10 所示。 图10 (a) 所示为被压缩后上法兰与MRS产生的接触面, 其长度为a。 图10 (b) 所示为上法兰与MRS 上表面之间产生的间隙流动模型, 在压力差p1-p2作用下, 流体在高为h的密封间隙中沿径向从内部向四周作稳定层流流出。
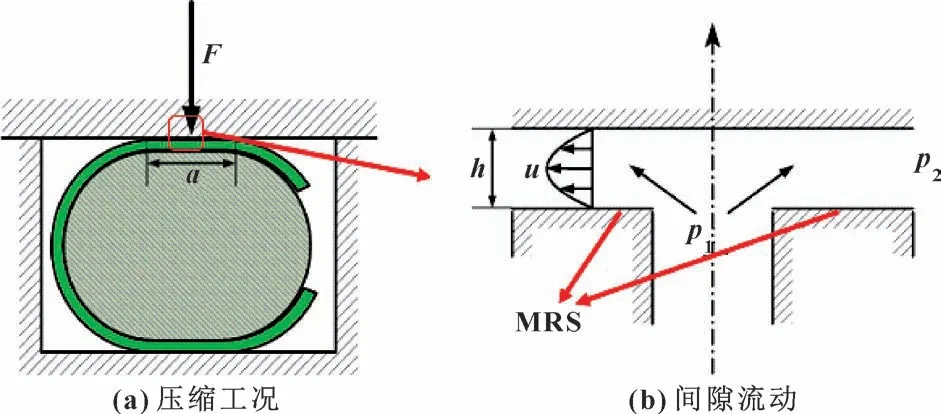
图10 MRS 密封件压缩后间隙流动模型Fig.10 Clearance flow model of MRS seals after compression:(a) compression condition; (b) clearance flow
根据上述间隙流动模型可以建立如图11 (a) 所示的流动域。 由于流动域环径比较大, 且泄漏间隙较小, 为了简化模型, 文中截取流动域的1/72 进行分析, 如图11 (b) 所示。 由于MRS 密封件截径较小,可以假设MRS 工作前后截面积不变, 由此接触长度a可由下式计算:
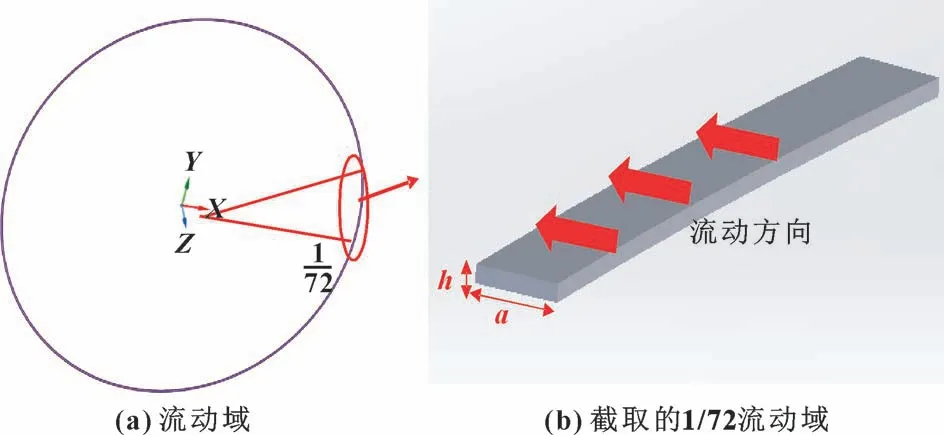
图11 密封间隙流动域Fig.11 Flow domain of seal clearance: (a) flow domain;(b) intercepted 1/72 flow domain
式中:S为MRS 密封件截面积 (mm2);R为MRS 密封件截径 (mm);H为压缩变形后的高度(mm);b为金属橡胶密封件非接触截面的1/2 长度(mm)。
H和b可由下式计算:
在预紧量δ=0.7 mm, 即压缩率为20%的工况下计算得到a=1.314 mm。 流动域间隙高度h可由下式计算:
式中:E为MRS 弹性体的弹性模量(MPa);p为密封介质压力(MPa);K为压力传递系数1.026。
式(5) 中的二重积分区域可简化为边长为2a的正方形区域, 其中E可由下式计算:
式中:σ为仿真计算得到的最大接触应力(MPa);d为MRS 截面的直径。
由式(5) 和(6) 可计算出间隙高度h=0.011 3 mm。
根据计算的接触长度a和间隙高度h可建立图11 (a) 所示的流动域。 采用型号为ISO VG320 的润滑油作为流体介质, 在流体出入口压差Δp=0.3 MPa下进行流体仿真计算, 得到了流体在MRS 密封间隙中流动的压力分布、 剪应力分布以及泄漏率的大小,如图12 所示。 从图12 (a)、 (b) 可以看出, 压力沿流动方向线性递减, 流体入口方向压力最大, 也即在MRS 包覆层靠近开口位置压力最大, 该位置最容易产生塑性变形。 从图12 (c)、 (d) 可以看出, 流动域出现许多细微的剪应力集中点, 但这些点沿径向的位置分布比较均匀, 因此在MRS 包覆层的上表面不会发生明显的剪切变形。
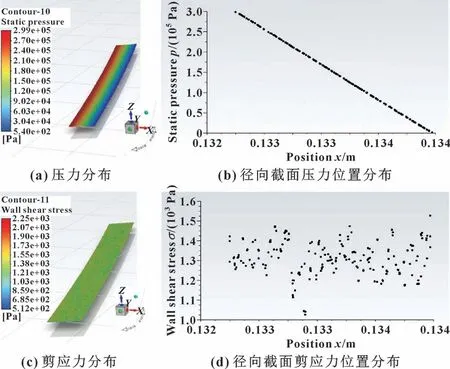
图12 流体仿真结果Fig.12 Fluid simulation results: (a) pressure distribution;(b) radial section pressure position distribution;(c) shear stress distribution; (d) radial section shear stress position distribution
为研究流体压差及压缩工况对密封件泄漏率的影响, 分别 在0.3、 0.6、 0.9、 1.2 MPa 压 差 下, 对10%、 15%和20%压缩工况下的MRS 进行了仿真计算, 得到不同压差和压缩工况下的泄漏率如图13 所示。 仿真结果与文献[9]中试验结果趋势较相符, 验证了仿真结果的正确性。 从图13 中可看出, 随着压差的增大, 泄漏率几乎呈线性增大; 而随着压缩率的增大, 泄漏率随之减小。 其中从压缩率15%增大到压缩率20%的泄漏率减小幅度明显小于从压缩率10%增大到压缩率15%的泄漏率减小幅度, 即随着压缩率的增大, 泄漏率减小的幅度随之减小。 由此可以得出, 可选择较大的压缩率来减少泄漏, 从而达到更好的密封效果。
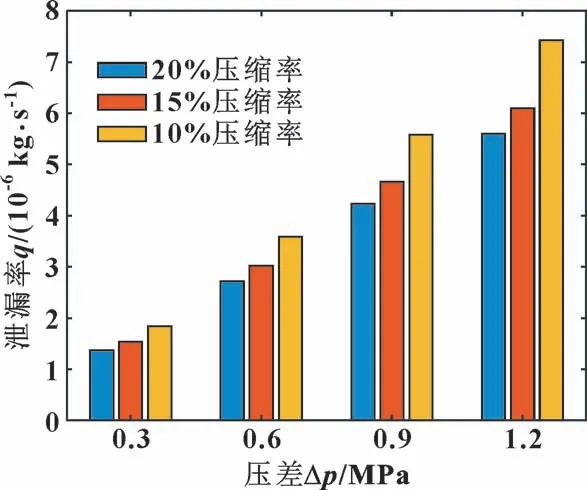
图13 不同压差下的泄漏率Fig.13 Leakage rate under different pressure
4 结论
(1) 针对大环径比圆形截面金属橡胶材料成型难等技术问题, 基于虚拟制备获得能反映MR 真实拓扑结构的有限元模型, 该模型在宏观力学性能以及细观纹理结构均与实际材料呈现了高度的一致性。
(2) 依据实际工况建立MRS 在预压缩工况下的密封模型以及流动域模型, 仿真结果表明MRS 在压缩工况的上表面容易产生绕周向的整体转动, 其接触特性受到压缩率及塑性变形状况的共同影响。 而在密封介质中, MRS 靠近流体入口的位置易承受较大的压力, 有发生塑性变形失稳和泄漏的风险。
(3) 在保证密封件不发生失效的前提下, 较大的压缩率会获得较大的接触压力并减少泄漏, 从而达到更好的密封性能。

