基于截面SEM 数据特征的微尘三维形貌建模方法

周林宏，何光宇，2，臧顺来，*

1．西安交通大学 机械工程学院，西安 710049

2．空军工程大学 等离子体动力学重点实验室，西安 710038

军用直升机或运输机面临在沙漠、战场前线等恶劣环境中起降情形，这些大气环境中常含有砂尘等微小颗粒物，其随空气被吸入发动机后，会对发动机压气机叶片产生砂尘冲蚀磨损，影响发动机的气动性能，严重时甚至导致发动机叶片的断裂失效，给发动机的可靠性和安全性等带来恶劣影响［1-3］。火星车在火星表面工作时，不可避免地会受到火星尘的影响，其中最直接的影响是微尘附着在太阳能电池表面导致太阳能电池输出功率下降。微尘环境对航空航天装备的运行性能有着不利影响，为加强航空航天装备的防尘设计需要对微尘展开研究。

微尘的几何形貌是影响砂尘冲蚀失效的重要因素，为探究砂尘冲蚀失效机理，需要研究微尘的几何形貌［4-6］；气固两相流对叶片气动特性影响研究中需要通过风沙颗粒的外形等相关特性进行研究［7-9］；微尘轨迹分析需要通过微尘的形状分布对其反弹特性进行研究［10］；同时微尘外形特征也是影响微尘吸附特性的重要因素。微尘的三维形貌是微尘特性的重要影响因素，因此研究微尘的形貌特征是加强航空航天装备防尘设计的关键所在。目前常用的微小颗粒物几何特征测量方法有测定颗粒粒径的沉降法、筛分析法、激光衍射法、电阻法，以及观察颗粒形貌的显微镜法［11-12］。每种测量方法都存在一定的适应范围及缺点。例如，沉降法存在测量速度慢，重复性差的缺点；筛分析法对于微小颗粒难以测量；激光衍射方法的测量误差与粒径分布与形状的不规则性存在正相关性；电阻法要求被测微小颗粒物具有良好的导电性；显微镜法代表性差无法获取具有统计意义的数据［13］。但仅通过分析测量仪器并不满足对于微尘颗粒形貌的研究需要，其他研究工作者也结合其他方法进行对颗粒三维形貌特征的探索，Komba 等［14］采用3D 扫描技术测量颗粒的形状指标，基于颗粒的表面积、体积以及3 个正交方向的长度数据描述了颗粒的形状特征。Alshibli 等［15］采用三维同步加速断层扫描技术获取了高分辨率的颗粒图像，并且使用光学干涉技术计算了颗粒的表面纹理。Sun 等［16］采用三维扫描设备，引入了“椭球度”的概念来衡量颗粒的三维形状。这些三维形貌的描述方法获得了较大颗粒的球形度等整体的形状参数，但是无法描绘更微小的颗粒以及颗粒的个体形貌特征。

传统方法对颗粒外形特征的描述均存在一定的缺陷。目前已有一些研究人员引入图像处理技术来研究微小颗粒物的三维形貌。 Jia 和Garboczi［17］总结了近年来，计算能力和三维图像采集与分析技术的进步，使得颗粒形状信息的测量、描述和应用取得的重大进展。Liang 等［18］引入了三维球度、圆度和粗糙度来定义粒子形态在一般形状、局部角度和表面纹理这3 个尺度级别来对颗粒的三维形态进行评价。Zhou 等［19］提出了一种评价颗粒形貌的DIP 方法，通过分析采集到的砂粒投影图计算砂粒轴径比以及圆形度。基于二维图像进行处理不能完整体现颗粒的三维形貌，因而其研究结果在多个个体的统计意义上才具有代表性，很难反映单一个体的几何形貌特性［20］。上述分析颗粒是通过各个方向二维的截面或者投影图像进行观测分析，由于颗粒具有三维的形貌，仅仅依靠二维图片只能分析某一特殊层的特征，不能完整地展现整个颗粒的形貌，而随着计算机技术的发展，通过计算机辅助重构出颗粒的三维表面，更有利于分析颗粒的三维形貌特征。Peng 等［21］通过多视图轮廓拟合和密集点云插值方法重建了磨损颗粒的三维表面。Zhou 等［22］在研究中采用计算机层析成像技术，重建了三维微尘的真实表面，提出了一种描述微尘三维球形度、圆度、和分形维数的方法，利用所提出的方法，对两种天然砂粒的形貌特征进行了测量。张永弟等［23］提出了一种层间插值算法，提高了三维重构准确性。

现有微尘三维重构方法对毫米量级的微尘形貌特征研究较为有效，但不能够满足粒径只有上述研究中1/10 甚至更小粒径微尘的重构需求，原因在于对更小粒径的微尘难以获取其不同断面之间的间距，因此微尘三维重构需要攻克难点和关键点是二维断层图像间距离的精确测定；而国军标砂尘冲蚀磨蚀标准中对细沙颗粒物粒度分布要求为0～200 μm［24］，因此对于更小的砂尘颗粒三维形貌测量方法和技术仍需开展深入研究。选取粒径100 μm 微尘作为研究对象，基于二维图像，在保持微尘间相对位置固定的前提下，通过逐层剥离获得高精度的微尘断层二维扫描电镜SEM图像。对于三维形貌重构，通过在微尘间隙预置一定直径钢球，利用钢球断层截面的圆心坐标变化规律，断层图像对齐；利用钢球断层截面圆的半径变化，实现断层层厚精确测定；基于距离变换的层间插值方法，有效提高断层间的分辨率，采用移动立方体算法重构了微尘的三维几何模型。

本文提出的方法将完成微尘的三维形貌表征，形成微尘外形特性分析方法，对推进航空装备的冲蚀防护、航空发动机气体动力学研究具有重要作用，对航空航天装备的防尘设计具有重要意义。

1 微尘断层图像试验

1.1 微尘冷镶试样制备

选取的研究对象为粒径100 μm 数量级（75～125 μm）的自制微尘。微尘试样采用冷镶的方法制备，制备微尘试样时，埋入直径1 mm 的精密钢球。采用切割机将试样切割为4 个部分，以消除试样的冷缩变形。用3 000 目砂纸打磨试样至露出钢球截面。将微尘试样放入喷金设备中喷金处理，喷金后试样见图1（a），每个视场内均埋入2 个精密钢球。

采用冷镶嵌的方法，微尘试样会产生固化收缩现象，使试样出现翘起、裂纹等问题。采用环氧树脂镶嵌出现的主要问题是固化后底面中心厚度会小于边缘厚度，见图1（b），厚度差约几十微米。由于采用的微尘粒径仅为75～125 μm，厚度差的存在会对图像采集造成不利的影响，因此将镶嵌后的微尘试样沿直径切割为4 个部分，得到4 个厚度差较小的试样表面，减小固化收缩带来的影响，见图1（c）。

图1 厚度差示意图Fig. 1 Schematic diagram of thickness difference

制备试样时，应将少量微尘颗粒与环氧树脂和固化剂混合均匀，以保证试样中微尘颗粒分布均匀，待固化与磨削工作完成后对制备的试样进行筛选，部分试样在光镜下的成像如图2 所示。图2 中深色部分为镶嵌基体，浅色部分为微尘截面，高亮部分为钢球截面部分。为了方便图像识别以及避免出现微尘堆叠从而影响三维重构的结果，应选取如图2（a）和图2（b）所示的图像中微尘分布间隔较远、堆叠可能性小的样品作为微尘重构研究的样品，应当避免选择如图2（c）和图2（d）所示的微尘密集分布，极有可能产生微尘颗粒堆叠的样品。

图2 微尘试样显微图像Fig. 2 Microscopic image of fine dust sample

1.2 断层图像

对微尘试样采用3 000 目砂纸进行逐层剥离并采用SEM 试验观察微尘的二维形状。视场1第1 层微尘截面的SEM 图像如图3（a）所示，图中白色为精密钢球，灰色为微尘截面，深色为样品镶嵌基体。微尘截面形状复杂多样，除几何形状接近凸多边形，还有细长状、断裂状、弯曲状等。图3（b）、图3（c）和 图3（d）为该 视 场 的 第6、11、15 层微尘截面的SEM 图像，随着微尘试样剥层的厚度增加，微尘截面形状出现增大或者减小趋势，也有一些微尘颗粒物消失。

图3 微尘断层图像Fig. 3 Tomographic image of dust particle

2 图像处理算法

2.1 微尘几何特征

2.1.1 阈值处理方法

为获取微尘二维截面轮廓，需要对图像进行阈值处理、去除图像杂质、提取边缘轮廓。其中阈值处理具体过程如下所述。一幅数字图像可视为一个函数f(x，y)，其中自变量是任意一像素点的坐标，函数值f为该点图像的灰度。阈值处理即图像的二值化［25］，阈值处理后f仅有2 个灰度值，0 或255。实现方法如下：首先给定一个合适的阈值Tcr，然后将整幅图像中大于或等于Tcr的像素点灰度值赋为255，小于Tcr的像素点灰度值赋为0，从而得到仅有0 和255 这2 个灰度值的二值图像函数g(x，y)，其数学表达式为

SEM 试验得到的图像中主要有3 种灰度等级，为了得到仅含有微尘截面和基体的二值图像，需要先将白色的钢球移除，然后再选择合适阈值将图像二值化。选择阈值T1cr=200，使灰度值大于T1cr的像素点灰度值变为0，其余像素点灰度值不变，完成钢球移除；选择阈值T2cr=40，使灰度值大于T2cr的像素点灰度值变为255，其余像素点灰度值变为0，完成图像二值化，视场1 第1 层微尘截面图像处理结果见图4。

图4 图像二值化Fig. 4 Binary image

2.1.2 移除小颗粒和边界微尘

二值化后的图像中通常含有杂质像素点，同时图像边缘的微尘截面并不完整，见图4（b）。为准确识别微尘截面轮廓，需要将这些杂质像素点移除。实现过程为：①在当前图像中标记连通区域，并计算每个连通区域的面积属性；②寻找面积小于50 像素的连通区域，并把这些区域删除，即把黑色区域中的白色杂质颗粒删除；③使黑白像素翻转，重复步骤①，删除白色区域中的黑色杂质颗粒，视场1 第1 层微尘截面的处理结果见图5（a）；④将图像边缘处的白色微尘截面删除，见图5（b）。

图5 去除杂质Fig. 5 Remove impurities

提取获得的微尘截面左上部分轮廓图像如图6 所示，微尘截面的轮廓边缘不完全光滑，存在凹凸不平的现象。

图6 微尘截面轮廓图Fig. 6 Profile of dust particle section

2.1.3 像素与微尘尺寸的转换

由于拍摄图像时的分辨率可以不同，则相同实际尺寸下对应的图像像素点个数也将存在不同。进行图像处理的基本单位是像素，而构建微尘三维模型需要使用微尘的真实尺寸，因此需要对像素个数与实际尺寸进行转换得到真实的尺寸。以图像的左上角为原点构建二维坐标系，截取图像当中的标尺部分，读取宽度方向的第1 个黑色像素坐标与最后1 个黑色像素坐标，得到标尺两端之间的像素数量，如图7 所示。采用标尺的实际长度除以像素数量可以得到单个像素对应的实际尺寸：

图7 图像标尺Fig. 7 Image scale

式中：L为单个像素代表的实际长度；l为选取标尺的实际长度；X1为标尺起始点像素横坐标；X2为标尺结束点像素横坐标。

2.1.4 提取微尘几何特征

对移除小颗粒后的二值图像提取微尘几何特征用于描述微尘的外形特性。如图8 所示，微尘二维截面轮廓几何特征指标的定义为最小二乘圆直径是对砂尘截面轮廓偏差最小的圆直径，其目标函数为

图8 微尘形貌表征参数Fig. 8 Characterization parameters of dust particle morphology

式中：FLSC为最小二乘圆算法条件下的总距离误差；x0、y0分别为最小二乘圆圆心横坐标、纵坐标；xi、yi分别为砂尘轮廓上第i个点的横坐标、纵坐标；R为最小二乘圆半径。

最小二乘椭圆长短轴是对砂尘截面轮廓偏差最小的椭圆长短轴，其目标函数为

式中：FLSE为最小二乘椭圆算法条件下的总距离误差；a为最小二乘椭圆短半轴；b为最小二乘椭圆长半轴；θ0为长半轴与x轴夹角；θi为砂尘轮廓上第i个点和最小二乘椭圆中心连线与长半轴的夹角。

最小外接圆直径是可以包容砂尘截面轮廓的最小圆直径，其目标函数为

式中：DMCC为最小外接圆直径。

最大内接圆直径是可以同砂尘截面轮廓内接的最大圆直径，其目标函数为

式中：DMIC为最大内接圆直径。

2.2 微尘三维重构

2.2.1 断层图像间距精确测定

二维断层图像间距离（层厚）的精确测定是基于二维图像进行三维重构方法的难点和关键点。预置的1 mm 高精度钢球在微尘试样中，随着微尘试样剥层的厚度增加，钢球截面轮廓圆半径会发生改变，根据半径变化规律可计算出相邻断层图像间的距离。通过截面中的钢球截面的半径变化来获取截面之间的厚度（见图9），当两截面位于同一半球，剥离层厚度为

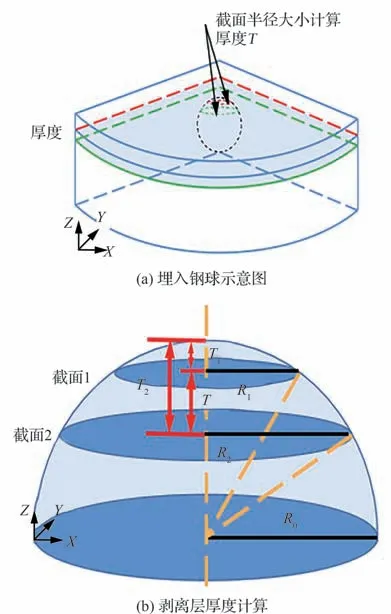
图9 断层图像间距示意图Fig. 9 Schematic diagram of tomographic image spacing

式中：R0为所用钢球的半径；R1为截面1 的圆半径；R2为截面2 的圆半径。

通过图像处理对截面图像进行识别得到钢球截面的半径大小，测定的截面半径大小存在一定的误差，因此计算的剥离层厚度也存在一定的误差。假设图像处理得到的截面圆半径的误差为ΔR，截面距顶端的距离为T1，T2=T+T1，基于此计算的厚度误差为ΔT，则

因此，

对于同一尺寸的钢球，即R0恒定，当两截面之间的距离T一定时，厚度误差ΔT与截面距顶端的距离T1有关，关系如图10（a）所示。随着截面尺寸越接近钢球的最大截面尺寸，厚度误差ΔT逐渐增大；当两截面位于两个半球时，误差有所降低。

当两截面之间的距离T和截面距顶端的距离T1一定时，厚度误差ΔT与钢球半径R0有关，关系如图10（b）所示。随着钢球半径R0的增大，厚度误差ΔT逐渐减小。

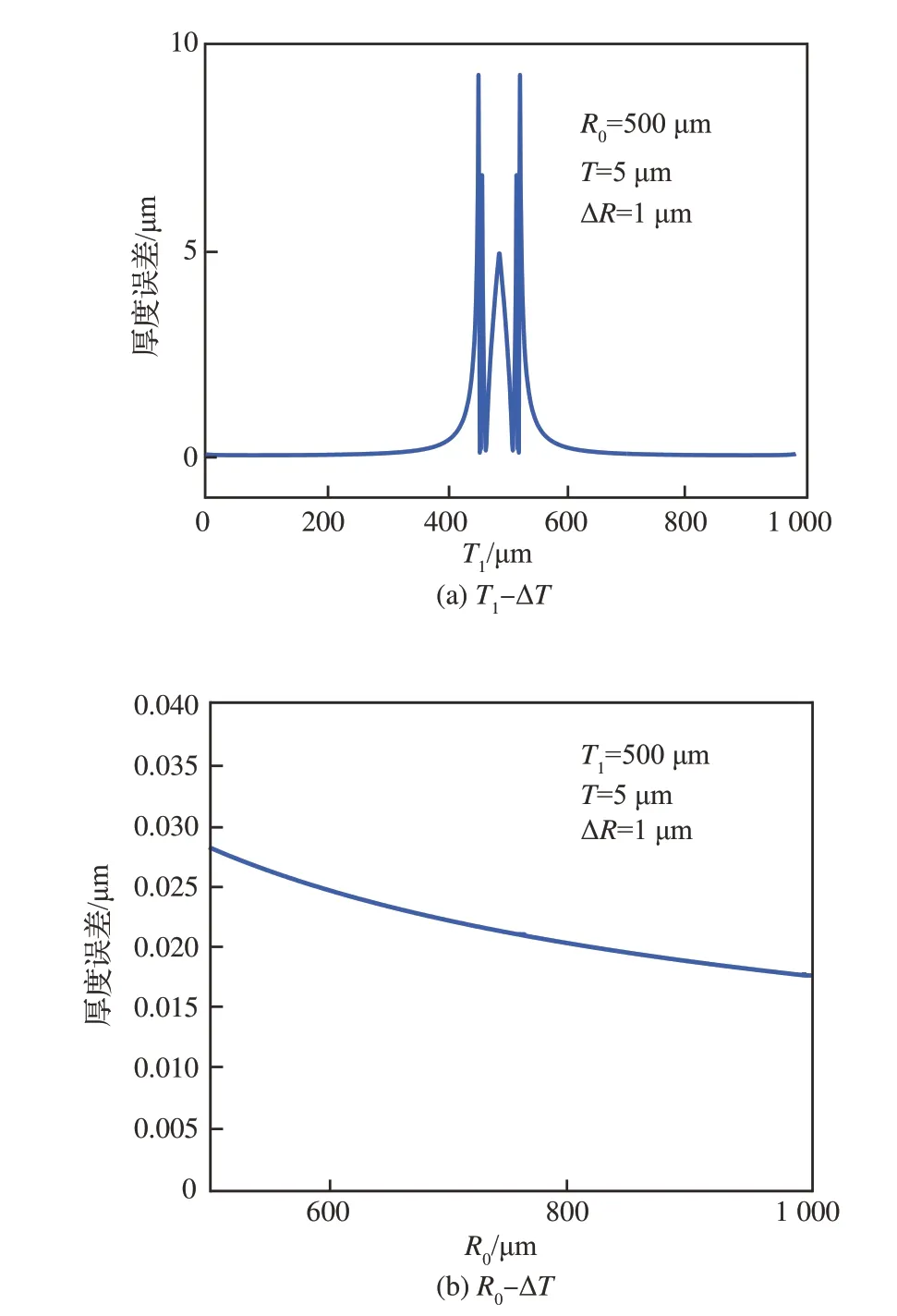
图10 厚度误差变化曲线Fig. 10 Thickness error change curve

2.2.2 断层图像间对齐

对于某一固定视场，拍摄过程会导致试样不同断层的截面图像并不在同一位置，即微尘的各个截面图像并未对齐，会导致重构得到模型发生偏移，无法还原目标的三维形貌，因此须调整截面图像中微尘的位置，以保证各个微尘的不同截面图像对齐。

基于图像处理的方法识别出各个断层图像中的精密钢球，并提取各个钢球截面的圆心。采用获取钢球圆心坐标的方法对图像提取钢球截面轮廓，获取构成钢球轮廓像素点的坐标，采用轮廓像素点横纵坐标的均值作为圆心坐标，根据轮廓区域面积获取钢球半径值，方法的主要误差来源于采集到的图像的精度以及磨削过程中钢球部分产生的毛刺。图11 为磨削后钢球截面部分的局部放大图像，图11（a）为带有毛刺的图像，图11（b）为进行过光滑的图像，对其进行圆心坐标和半径的获取得到的结果分别为（1 561.1，497.7）、（1 560.1，497.9）以及85.4、85.3，单位为像素，转化为长度单位则圆心坐标产生的偏差为横坐标方向1.796 μm、纵坐标方向0.359 μm，半径产生的偏差为0.18 μm，约为半径值的0.11%。因此磨削过程中钢球的毛刺对钢球截面圆心坐标以及半径长度的获取影响较小。

图11 钢球磨削产生的毛刺Fig. 11 Burr from grinding of steel ball

以图像中心（1 024，768）为原点，设第k层截面中第i个钢球的截面圆心坐标为Xik，下一截面的第i个钢球的截面圆心坐标为Xik+1，每个截面的钢球数量为2 个，可以求得第k层钢球截面圆心间的正切值为

式中：X2k(2)、X1k(2)为图像中第2 个和第1 个钢球圆心的纵坐标；X2k(1)、X1k(1)为图像中第2 个和第1 个钢球圆心的横坐标。

包含坐标旋转变换参数θ的坐标变换矩阵为A(θ)。要保证前后图像截面中的钢球对齐，即要求的θ，满足

包含坐标平移参数j、q坐标变换矩阵为B(j，q)，要保证前后图像截面中的钢球对齐，即要求的j、q，满足

图12 是选取视场1 的第2 层截面图像对齐前后的对比图。图中，横向与纵向平移变化以及旋转角度分别为22.183 1、23.757 9、0.287°，旋转中心为图像中心。

图12 图像对齐Fig. 12 Image alignment

2.2.3 三维重构算法

三维重建算法主要可以分为面绘制与体绘制，其中面绘制在运算速度与运算量方面更有优势，是三维重建中的主流方法。其中移动立方体（Marching Cubes， MC）算法［26］应用最为 泛。MC 算法是一种用提取等值面（用三角面片近似表示）来表示物体表面的方法，见图13。本文采用MC 算法进行微尘模型的三维重构。

图13 移动立方体算法示意图Fig. 13 Schematic diagram of moving cube algorithm

通过SEM 试验拍摄得到的二维断层图像分辨率为2 048×1 536，通过像素与实际长度的换算得到单个像素所代表的实际长度为1.796 μm，若断层图像之间的厚度大于1 μm 则进行插值至层间间距小于1 μm；单个微尘颗粒根据其体积大小，体素数量在40×40×200 至150×150×300 区间内；编写图像处理及三维重构程序，采用个人计算机进行重构，单个微尘颗粒重建时间为2.3 s。

为对该算法进行验证，自主构建标准三维模型与随机三维模型如图14 所示，通过Materialise Magics 模拟逐层磨削过程，获取断层图像进行三维重构，重构结果如图15 所示。可以看到得到的重构结果与构建模型近似。

图14 自主构建模型Fig. 14 Self-built models

图15 验证结果Fig. 15 Verification results

2.2.4 断层图像层间插值

在对断层图像进行三维重建的过程中，一般而言断层间的距离大于断层图像像素间的距离。导致断层图像的层间的分辨率低于层内的分辨率，影响了三维重建的质量。采用层间插值的方法来提高层间的分辨率，即用图像插值的方法在原来的断层图像间再生成中间断层图像。而层间插值处理中存在的主要问题是当断层图像间距大时，没有任何方法可以插值出好的中间图像即无法判断两个断层图像之间是否存在物体“消失”或“拓扑变化”现象，因此只有满足断层图像间距较小时可以采用层间插值方法。

计算得到的断层图像间的间距为4～8 μm，而拍摄得到的图像中，单个像素换算实际长度为1.796 μm。因此断层图像间的间距约为平面图像中2～5 个像素的长度，满足在断层图像间距足够小的条件，因此可以忽略断层图像间的物体“消失”或“拓扑变化”现象，采用线性插值的方法进行近似插值获取层间近似图像。

关于插值模型，假设有2 幅二值图像分别命名为gk和gk+1，并假设两目标图像为分别位于两平行平面Z=Zk和Z=Zk+1上，对这两目标图像进行层间插值即得到在一系列平面Z=Zm(Zk＜Zm＜Zk+1)上生成的目标图像gm，并使gm相似于gk和gk+1。

3 结果与讨论

通过图像处理得到了微尘截面轮廓图，微尘截面轮廓的边缘不完全光滑，存在凹凸不平的现象。通过图像处理提取的微尘几何特征参数如表1 所示，选用的微尘试样的粒径参数为75～125 μm，结果中微尘截面最小二乘圆直径分布在0～130 μm 之间，约75%分布在55～100 μm 范围内；试验测定中微尘粒径相对标准粒径偏小，这是由于SEM 实验所得到的是靠近微尘边缘处的截面图像，因此实验得到的微尘粒径相对于标准值偏小。试样的最小二乘椭圆长轴分布在0～150 μm 范围内，最小外接圆直径分布在25～200 μm 范围内，存在一部分微尘截面的最小外接圆直径大于最小二乘椭圆长轴；最小二乘椭圆短轴分布在0～125 μm 范围内，最大内接圆直径分布在0～125 μm 范围内，存在一部分微尘截面最大内接圆直径小于最小二乘椭圆短轴，说明存在部分微尘呈现细长状。

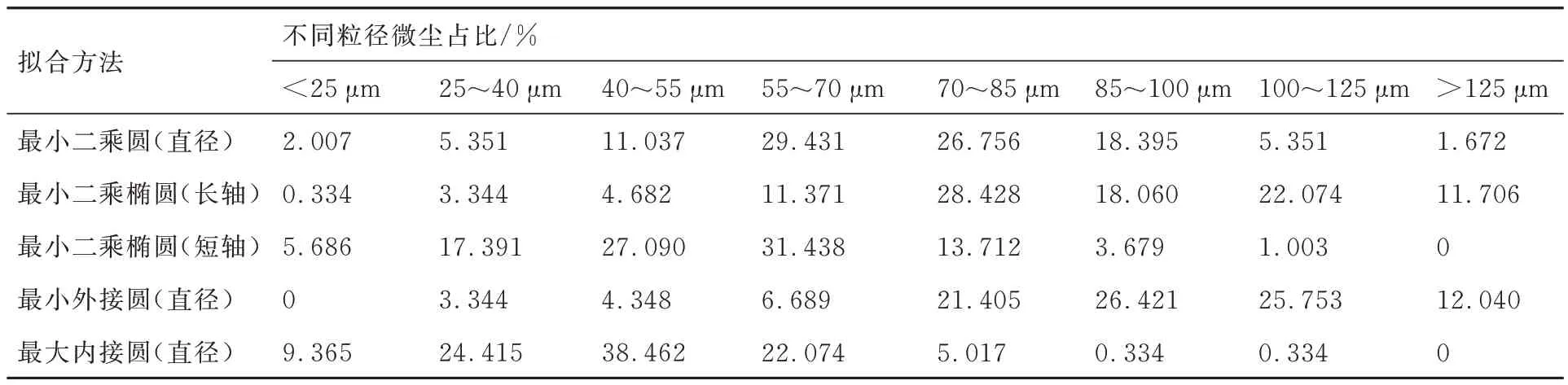
表1 微尘几何特征Table 1 Geometric characteristics of dust particle

对于最小二乘圆直径，试样中55～100 μm 范围的微尘最多，约占整体的75%；对于最小二乘椭圆长轴，试样中70～125 μm 范围的微尘最多，约占整体的70%；对于最小二乘椭圆短轴，试样中40～85 μm 范围的微尘最多，约占整体的70%；对于最小外接圆直径，试样中70～125 μm范围的微尘最多，约占整体的75%；对于最大内接圆直径，试样中25～70 μm 范围的微尘最多，约占整体的75%。每个试样的5 个参数之间均存在一定的差异，因此微尘中仅存在少量接近圆形的微尘截面。

根据移动立方体算法重建得到了500 个微尘的三维模型，其中几种典型的微尘三维模型如图16 所示。其中常见的微尘形状分为不规则多棱角状（见图16（a））、规则棱柱状（见图16（b））、尖角状（见图16（c））、规则多面体状（见图16（d））、棱锥状（见图16（e））、扁平片状（见图16（f））、长条状（见图16（g））、阶梯状（见图16（h））、凸台状（见图16（i））。而典型砂尘冲蚀仿真中所采用的微尘模型多为球状、棱柱、棱锥等［4-6］，与真实微尘的形貌有着较大的差别，可以推测采用真实的微尘模型进行有限元数值模拟将有利于提高砂尘冲蚀计算的精度。

图16 几种典型的微尘形貌Fig. 16 Typical dust particle morphologies

4 结 论

1）通过断层图像中钢球截面的直径变化，完成了微尘断层图像间距的精确测定，解决了基于断层图像进行微尘三维重构中断层间距难以获取的问题。

2）提出了一种基于断层图像插值的微尘三维形貌重构方法，获取了微尘的三维重建模型，分析了100 μm 数量级微尘的几何特征参数与形貌特征。

3）通过对微尘截面的图像处理，提取了500 颗微尘的几何特征参数，获取了具有统计意义的微尘几何特征参数，微尘粒径分布呈现正态分布，部分微尘呈现细长状，同时微尘中仅存在少量接近圆形的截面。

4）完成了500 颗微尘的三维重构，得到了9 种典型的微尘三维模型，与现阶段研究中理想化假设的微尘模型存在较大差距。