小展弦比飞翼标模非定常流动及自由摇滚特性

王方剑，解克，刘金，宋玉辉，秦汉，陈兰

中国航天空气动力技术研究院，北京 100074

飞翼是一种高度融合翼身组合体布局，全机没有平尾、垂尾等安定面，也没有传统意义上的机身，在外形上体现出平滑过渡、高度融合的几何特征，使战斗机在各种高度、姿态下的隐身性和机动性都得到很好的兼顾，是实现隐身/气动一体化设计的理想选择。国内外在以战斗机为背景的飞翼布局研究中，主要集中在中小展弦比飞翼布局，其中典型的有4 个研究外形：NASA 的ICE 外 形［1］、国 际 合 作 计 划 中 的1303 外 形［2］、NATO/RTO AVT-161 项 目 组 采 用 的SACCON 外形［3］以及中国“十二五”期间自主研发的小展弦比飞翼标模（FDM）［4］。

在飞翼布局静态流动特性方面，Tormalm等［5］分别采用SA、SARAL、SST 湍流模型以及DDES 方法对SACCON 外形静态流场进行计算并对比分析，分析表明在小攻角区域，SARAL、SST 湍流模型都能够得到较好的模拟效果，而在较大攻角区域，对背风侧分离区的模拟建议采用DES 方 法 模 拟 复 杂 的 流 动 结 构。Frink［6］分 析 了SACCON 随攻角增加，背风侧的流动发展非常复杂，存在头部涡、厚度涡、翼尖涡，攻角增加之后厚度涡与翼尖涡融合成为一个大涡，体现出飞翼布局复杂的流动特性。苏继川等［4］通过数值模拟研究了小展弦比飞翼标模的跨声速典型气动特性，主要以涡升力为出发点，分析了涡的产生、发展直至破裂的整个过程。张耀冰等［7］采用数值模拟方法研究了雷诺数对小展弦比飞翼标模流场气动特性的影响问题。结果表明大攻角时，雷诺数增大，除引起摩阻减小外，压阻也有明显增大。

对于无尾布局飞行器非定常流动特性研究主要集中在三角翼模型上，Gursul［8］在试验中发现三角翼旋涡的破裂点会沿着涡轴进行振荡，并研究了前缘后掠角对振荡频率的影响。Menke等［9］通过采用风洞试验方法，将三角翼的流动频率分为4 种模态，分别是涡破裂点振荡频率、涡脱落频率、螺旋波的失稳频率、剪切层的失稳频率。当模型攻角逐渐增大，先出现的是旋涡破裂（一般是螺旋式破裂），涡破裂点出现非定常振荡，并且其频率特性与后掠角相关。试验发现［10］旋涡破裂的频率由准周期的频率以及高频率低幅值的振荡组成，与此同时还伴随着非对称涡的位置左右切换，随着攻角增加，涡破裂点沿涡轴前移，左右旋涡干扰加剧。祝立国和吕志咏［11］也在水洞中发现了此现象，Ericsson［12］在之后的研究中详细分析了旋涡破裂的流态及其频率特性。张明禄等［13］对75°后掠三角翼进行脉动压力测量，发现通过对信号的滤波处理，可知整个三角翼上翼面的压力脉动以螺旋波的影响为最大，破裂涡流中螺旋波的准周期压力脉动造成了机翼的抖振。Li［14］和Lin［15］等采用数 值模拟方 法，对双 三角翼的大攻角涡破裂特性进行分析，发现了破裂形态的转换、破裂点的振荡和破裂后螺旋涡结构的脱落，气动力频率特征决定于螺旋涡结构的脱落频率。

飞行器大攻角飞行时，由于背风侧分离流动极为复杂，易引发运动失稳，其中较为常见的为以绕体轴滚转振荡为主的机翼摇滚运动。Ross等［16］对大量战斗机非指令运动进行统计研究，将机翼摇滚现象分为两类，一种为跨声速较小攻角下的机翼摇滚运动［10，17］，其运动失稳的主要原因为激波诱导的流动失速；另一种主要发生在低、亚声速，在较大攻角出现的机翼摇滚运动主要由前体涡、机翼涡相互干扰带来。 Ericsson等［12，18-21］在 机 翼 摇 滚机理方面做了多方面的工作，在理论方面做出了基础性的贡献。唐敏中［22］、邓学蓥［23］、王方剑［24］、杨晓峰［25］等采用风洞自由滚转试验、流动显示的方法，对细长体机翼摇滚的机理做出了很有意义的研究，刘伟［26-27］、杨云军［28］等采用数值模拟方法，对细长三角翼在摇滚过程中的流动变化进行进一步的深入分析，并采用非线性动力学方法对其运动历程进行建模，取得很好的成效。

从飞翼布局流动特性研究现状可以看到，相比于三角翼，飞翼布局复杂的外形设计会对流动特性产生较大影响，并且对于飞翼布局流动特性的研究主要集中在定常流动范畴，对于飞翼布局的非定常流动以及运动失稳特性研究较少。本文采用延迟脱体涡模拟（DDES）方法模拟飞翼标模单自由度自由摇滚运动，并采用动力学模态分解（DMD）、物面脉动压力分析等方法分析飞翼标模非定常特性、自由摇滚机理，为中国飞翼布局飞行器的研制提供理论支撑。

1 DDES 方法及算例验证

控制方程为三维可压缩Navier-Stokes 方程，广义坐标表示为

式中：F、G、H为对流通量；Fv、Gv、Hv为黏性通量。

空间离散采用基于MUSCL 插值方法的FDS-Roe 格式，黏性项采用二阶中心差分离散，对流和压力项使用三阶迎风偏置格式。时间推进格式为隐式LUSGS 方法，保证了较高的时间计算精度。非定常计算采用双时间步长方法，同时采用多重网格算法加快子迭代的收敛速度。在用湍流模型进行流动模拟时，控制方程中应加入雷诺应力相关项。本文采用的湍流模型是基于Menter 的两方程剪切应力输运湍流模型（SST），表达式为

为了具有DES 性能，DES 方法的一般思想是重新定义SST 湍流模型k方程的耗散项，其形式为

为了解决MSD（Modeled Stress Depletion）与GIS（Grid Induced Separation）问题，Spalart等［27］提出了延迟函数fd，将SST 湍流模型的湍流能量输运方程的耗散项重新定义为与网格尺度和湍流黏度有关的DES 长度尺度。延时函数的表达式为

式 中：Ui，j为速度梯度；υt为湍流黏度系数；κ=0.41 为卡门常数；d为网格到物面的距离。结合延迟函数fd的长度尺度dDES被重新定义为

因此，dDES不仅与网格尺度有关，而且与湍流黏度有关，可以防止湍流模拟过早地切换到LES模式。

采用基于三阶迎风偏置格式的DDES 方法来开展研究，主要基于以下考虑：

1） DDES 方法对网格依赖性较好，能够增强RANS 与LES 分界面的识别和过渡能力，从而减少人工计算参数设置带来的不确定性。虽然DES 类方法存在固有的“灰区”问题，在局部位置对小尺度湍流脉动解析会引入数值模拟误差，但小尺度旋涡能量较低，诱导物面产生的附加气动力较小，对整体流场结构及大尺度旋涡演化规律影响较小，所以可认为该方法是适用的。

2） 三阶迎风格式与中心格式相比耗散相对较大，这会影响对小尺度旋涡的解析。但由于本文重点在于对机翼摇滚及其非定常现象的研究，小尺度旋涡特征频率比飞行器摇滚频率高两个量级，小尺度、高频率的湍流脉动将难以对飞行器的整体运动构成明显影响。因此，这里选用迎风型格式来开展研究理论上是可行的。

测试算例采用的计算外形为NACA0021 翼型，翼型弦长为125 mm，展长为500 mm，翼型两端采用周期边界条件。计算网格采用结构网格进行求解，总数为500 万，图1 展示了横截面网格分布，为了保证对翼型后缘微小分离的模拟精度以及翼型背风侧的大尺度分离流动的模拟效果，在进行网格划分时，分别在翼型后缘与模型的背风侧法向进行了加密。由于算例计算风速为低速，在计算时引入预处理，使得计算鲁棒性与精度都得到了相应的提高。计算参数为：Ma=0.1，攻角为α=60°，Re=0.27×106，物理时间步为1×10-4s，共计算了10 000 个物理时间步，计算物理时间为1 s。图2 为NACA0021 横截面的瞬时涡量，从图中可以看到，通过采用DDES 计算方法，能够捕捉到NACA0021 翼型背风侧的复杂且丰富的旋涡结构。

图1 横截面网格分布Fig. 1 Mesh of cross section

图2 NACA0021 横截面瞬时涡量Fig. 2 Transient vorticity of NACA0021 cross section

图3中黑色曲线为模型中间横截面的压力Cp分布时均值，红色空心圆点为风洞测压试验中相应截面的压力分布。从图中可以看到，试验值［29］与计算值在量值上和趋势上都保持了较好的一致性，证明SST-DDES 方法在气动力计算上能够取得较好的效果。图4 为计算值与试验值的频谱对比情况。横轴为斯特劳哈尔数St，纵轴为功率谱密度PSD。红色曲线为通过风洞试验测得的升力时序数据辨识出的频谱，黑色曲线为通过CFD 方法得到的升力功率谱。从图中的对比能够看到，试验值与计算值在量级上与趋势上都能够得到吻合较好。计算值能够捕捉到背风侧流动的主频（St=0.2），同时能够捕捉到2 倍频（St=0.4），说明SST-DDES 方法在时序过程以及频率捕捉上也能够有比较好的计算效果。

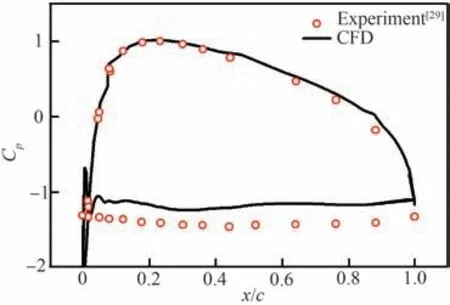
图3 试验与计算压力分布对比Fig. 3 Pressure distribution comparison between experiment and CFD

2 动力学模态分解方法

动力学模态分解（DMD）方法只基于流动快照而不受模型限制，通过提取流动中的模态，准确地描述流动结构。对于非线性流动而言，DMD 的模态描述了在数据序列中起支配作用的流动结构。其基本思路是基于线性化假设，假设每一个瞬时的物理量都可以用前一个瞬时线性表示，求解变换矩阵的相似矩阵，对相似矩阵进行特征分解得到对应的流动模态，其优势在于，每阶模态对应都是单一频率，所以对于多频复合的复杂流动下，分析单一频率下的模态特性，能够对研究复杂物理现象有一定的参考意义。以下为其数学推导过程。

DMD 方法假设每一个瞬时物理量可以用前一个瞬时线性表示，所以定义n个流场快照中，前n-1 个流场快照为X，后n-1 个流场快照为Y，所以可以表示为

式（9）中A表示线性变换矩阵，由于每个流场快照数据量非常庞大，这样矩阵A的维度就会非常大，不便于求解。所以DMD 方法是通过求解A的相似矩阵来实现。对X进行奇异值分解，得到左奇异矩阵U以及右奇异矩阵V。其中Σ为奇异值矩阵，选取前r阶奇异值，从而得到降阶的效果。同时将矩阵A向U方向投影得到式（11）。

将式（10）、式（11）代入式（9），得到相似矩阵的表达形式如下：

将相似矩阵进行特征分解，得到主要特征值和特征向量，记第j个特征值和特征向量为μj和wj，则定义第j个模态为

其对应的模态频率为

最终每个瞬时的流场快照都可以表示为模态、振幅、动力学矩阵乘积。

3 小展弦比飞翼标模及计算网格

采用国内小展弦飞翼布局标模［4］，其三维示意图与坐标如图5、图6所示。模型缩比为1∶25，模型总长L=0.612 m，翼展Span=0.457 m，参考面积S=0.131 6 m2，平均气动弦长（参考长度）c=0.382 m。计算马赫数：Ma=0.6，攻角α=0°～30°，侧滑角β=0°，Re=8.5×106，力矩参考点为（0.352，0，0.016 5）m，机头顶点为坐标原点。

图5 小展弦比飞翼标模外形尺寸Fig. 5 Configuration of low aspect ratio flying-wing

图6 飞翼标模坐标Fig. 6 Coordinate system of flying-wing

图7为网格空间拓扑结构，全流场采用全O型结构网格，远场距物面距离为20 个参考长度，y+＜1。为保证对流动分离细节的捕捉，在飞行器头部、机翼前缘、翼稍进行适当加密，在模型旋涡相应位置的法向与周向也进行了适当加密。

图7 网格空间拓扑图Fig. 7 Mesh space topology

由于针对的是飞翼布局大攻角下非定常流动特性问题，其对旋涡尺度的分辨十分重要，所以需要对网格无关性进行检查，图8 为飞翼标模物面网格拓扑结构，网格量分别为750 万、1 500万、3 000 万，3 套网格在流向、周向、法向均进行变化。选取的典型工况为Ma=0.6，α=24.5°，并选取升力CL、阻力CD和俯仰力矩Cm的平均值进行分析。表1 为3 套网格下的升力CL、阻力CD、俯仰力矩Cm计算结果。从表1 可以看到，网格规模对CL、CD、Cm均有一定的影响，随着网格量的增加，当网格量达到1 500 万时，其计算结果（CL、CD、Cm）与网格量3 000 万较为接近，证明网格量1 500 万对于研究该问题已满足要求。

图8 物面网格Fig. 8 Surface mesh

4 飞翼标模静态流动特性

图9 为Ma=0.6 下攻角α=0°～30°范围内的流动变化，从图中可以看到，攻角α=5°时，飞翼标模在翼稍开始卷起对称涡流动结构，旋涡起始点在距头部顶点X/L=0.6左右，随着攻角持续增大至α=15°，对称涡起始点逐渐移动至模型顶点，当攻角增大至α=20°时，集中涡变得不稳定，开始出现涡破裂现象，并且模型两侧旋涡开始呈现明显的非对称形态，随着攻角继续增大至α=30°，旋涡破裂点逐渐向头部移动，旋涡破裂后呈现出尺度较小的螺旋旋涡结构，流动也体现出了明显的非定常流动特性。

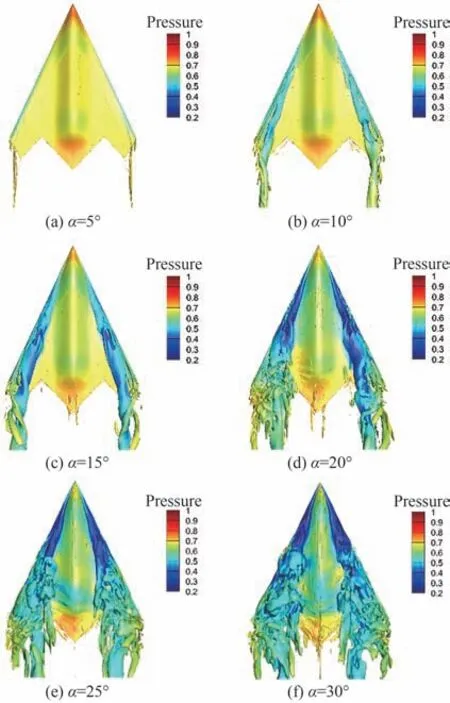
图9 飞翼标模静态流动变化Fig. 9 Static flow of flying-wing

5 飞翼标模非定常流动特性及DMD 分析

飞翼标模在大攻角下具有非常复杂的非定常流动特性，本节以亚声速为例，对其非定常流动特性进行细致分析，计算Ma=0.6，攻角α=26°，计算物理时间步长为5×10-5s。如图10 所示，从图中可以看到，飞翼标模出现了类似三角翼典型的分离涡、涡破裂、螺旋波结构。飞翼前缘诱导分离集中涡，从模型头部起始，沿流向向后发展，其中涡轴速度在X/L=0.4 位置降至很低，随即发生旋涡破裂，在旋涡破裂处，涡量由于无法继续沿涡轴向后发展，会由内而外产生螺旋波流动。为了更好的研究空间流动对物面局部压力分布的影响，在旋涡影响较大的区域布置监测点，如图10 所示，其中沿涡轴布置了5 个点，分别监测流动对物面的诱导能力，其在物面X方向位置分别为X/L=0.28，0.41，0.5，0.56，0.7。

图10 物面监测点布置（Ma=0.6）Fig. 10 Location of monitored points （Ma=0.6）

图11是飞翼标模空间流动随时间的变化，从图中可以看到，随着时间变化，旋涡飞翼旋涡破裂位置随着时间也会有一定程度的变化，当时间t=0 s时，旋涡破裂位置在X/L=0.25 的位置，随着时间推移，其旋涡破裂位置逐渐向下游移动，当t=3.0×10-3s时，旋涡破裂发展到约X/L=0.3的位置，然后旋涡破裂位置继续向头部方向移动，从以下图中也可以看出，即使飞翼标模是静止的，旋涡破裂位置也会在一定范围内变化，频率较低，而螺旋波流动体现出的是一种高频的流动变化。图12 是沿旋涡涡轴切面的涡量值随时间变化，依然能够较为明显的看到旋涡破裂位置随时间的变化。在旋涡破裂以前，涡量处于稳定的状态，旋涡破裂以后，涡轴的涡量分散成若干高频小尺度涡向后发展。这也体现出了飞翼标模在大攻角下，背风侧复杂非定常流动由不同尺度、不同频率的流动组合而成。

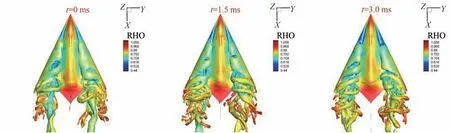
图11 非定常旋涡流动随时间变化（α=26°，Ma=0.6，FDM）Fig. 11 Unsteady vortical flow of flying-wing vs time（α=26°，Ma=0.6，FDM）

图12 涡轴切面涡量分布（α=26°，Ma=0.6，FDM）Fig. 12 Vorticity distribution on section of vortex axis（α=26°，Ma=0.6，FDM）

图13是旋涡破裂点在x方向的位置随时间的变化，从图中可以清晰的看到，旋涡破裂点随时间呈现出明显的非定常性，其变化范围在X/L=0.29～0.45，波动范围为模型全长的16%左右。

图13 涡破裂点位置随时间变化曲线Fig. 13 Location of vortex breakdown point with time

图14是监测点非定常压力脉动，中间一列曲线为压力（P/Pinf： 当地压力除以来流压力）随时间变化，右侧为其对应的频谱。从图中可以看到，在不同的测压点由于空间流动不同，诱导出了不同的压力脉动特性。在X/L=0.28 处，能看到其压力脉动幅值很小，只是有一些微小的波动，从频谱中也没有看到明显的频率，此处为稳定的集中涡，所以没有明显的脉动特性。在X/L=0.41 处，空间流动处于旋涡刚破裂的区域，由于旋涡破裂点会随着时间的变化沿涡轴前后移动，所以在压力脉动上产生了较为明显的脉动，从频谱中能够发现，其中主要频率St数（St=fc/V∞）在0.12～0.23左右，也揭示了旋涡破裂的主要频率在这个范围。在X/L=0.5，0.56 处，旋涡已经发生破裂，并且旋涡破裂点不会下移到此位置，此处流动为涡破裂后的“泡型”膨胀区域，从脉动压力上能够看到，此处的脉动压力值较小，没有体现出很明显的主频，X/L=0.5处，由于受上游涡破裂点移动的影响，在频谱上轻微的体现出了主频范围，与X/L=0.41 处频率范围接近，而X/L=0.56 处，涡量已经充分膨胀，没有体现出明显主频。当流动发展至X/L=0.7，涡量膨胀后开始诱导出高频的螺旋波流动结构，其中诱导的压力幅值开始变大，从频谱中可看到，其主频范围为St=1.16～2.33 范围内，体现出了螺旋波的高频特性。

本文还采用了DMD 方法对Ma=0.6、α=26°工况下大攻角非定常流动进行初步分析，共计算了300 个瞬时空间流动，时间间隔为5×10-4s。由于直接计算全流场的DMD 分解会带来极大的计算量，所以这里将沿涡轴切面作为表征面来进行分析，将这300个表征面的速度值进行DMD 分析，并提取出流动模态对应的频率。图15为不同频率对应的DMD 模态，可以看到，其中St=0对应模态体现为典型的涡破裂形式，沿涡轴方向速度值在涡破裂前较大，破裂后速度迅速降低，并产生一定回流，该模态类似整体流动的“平均值”，体现了旋涡流动的总体效果。在St=0.25 模态中发现，在涡破裂位置附近体现出了一定的流动非定常变化，同时在下游也体现出了一定的小尺度流动，该模态频率也在旋涡破裂点振荡频率范围内。在St=0.39 模态中，可以看到，涡破裂点处已经没有明显的脉动特征，该频率下的流动主要体现为下游的小尺度流动，同时有一定的旋涡脱落以及切换特性。在St=1.2 模态中，可以看到，该模态频率在螺旋波频率内，从模态中也能够比较清晰的看到，更多更小尺度的旋涡脱落与切换出现在接近模型尾部的地方，这也是受空间螺旋波流动影响的一种直接体现。

图15 涡轴切面速度值DMD 模态分析Fig. 15 DMD modal of section of vortex axis

6 飞翼标模自由摇滚特性

为研究飞翼标模在Ma=0.6 下的单自由度横向失稳运动，采用风洞试验与数值模拟结合的方法进行研究。风洞试验是在中国航天空气动力技术研究院FD-12 风洞中进行，飞翼标模横向无量纲转动惯量I*=36.5，无量纲方法为

式中：ρ=1.15 kg/m3为来流密度；A=1.2 为展弦比。

流动/运动耦合策略采用紧耦合方法，并引入了“预估-校正”机制，在双时间步的内迭代过程中，流动与运动同时收敛，提高系统稳定性。

六自由度运动方程可采用与流动控制方程相同的时间离散方式，根据线性多步法松弛迭代求解，松/紧耦合可用统一的形式描述［30］：

式中：Q6DOF为运动学参数；F6DOF为飞行力学控制方程通量；g、h、ω为松弛因子；a、b、c、d、e为系数。选取不同的系数即可得到不同的时间精度和耦合方式的计算方法，见表2，本文采用的方法为表2 中 的BDF2（2nd-Backward-Difference Formula）方法。

表2 飞行力学离散控制方程系数Table 2 Coefficients of discrete governing equations of flight mechanics

时间步长对自由摇滚准确捕捉也有一定的影响。采用dt=2.25×10-4，4.57×10-4，6.30×10-4，9.00×10-4s 这4种时间步长对Ma=0.6、α=24.5°工况进行测试，图16 为时间步长对自由摇滚时间历程的影响，从图中可以看到，不同的时间步长对摇滚历程频率影响很小，对局部滚转角峰值有一定影响。随着时间步长不断减小，当时间步长减小至dt=4.57×10-4s 时，其滚转角峰值几乎不随时间步长变化，证明时间步长dt=4.57×10-4s 已满足计算要求。

图16 不同时间步长对摇滚历程影响Fig. 16 Effects of time step on wing rock

图17（a）为飞翼标模自由滚转风洞试验滚转时间历程；图17（b）为滚转角平均振幅随俯仰角的变化，俯仰角运动范围为22°～24.5°，图中显示，当标模在0 s时刻放开后，飞翼标模平衡滚转角迅速调整至10°左右，滚转角存在轻微抖动。随着俯仰角逐渐增加，当俯仰角增加至24°时，平衡滚转角继续增大至27°附近，当俯仰角达到24.5°时，标模平衡滚转角增大至28°，并且其横向振荡振幅突然增大，出现了自由摇滚运动。所以飞翼标模出现的摇滚运动为平衡位置偏向一侧（平衡滚转角为±28°左右）极限环运动，这与三角翼摇滚运动有一定的不同。

图17Ma=0.6 自由摇滚试验结果Fig. 17 Wind tunnel test of wing rock （Ma=0.6）

通过CFD/RBD 方法，同样捕捉到了飞翼标模的自由摇滚运动及CFD 方法获得的飞翼。图18（a）为滚转角变化时间历程计算结果与试验结果的对比，图18（b）为二者的频谱对比。图中显示，计算结果与试验结果获得的滚转角时间历程的平衡位置均为28°左右，计算结果振幅与试验结果相比偏大，计算获得自由摇滚平均振幅为12°左右，风洞试验获得平均振幅为8°左右。从频谱分析可以看到，试验摇滚减缩频率k（无量纲化k=fc/（2V∞））为0.008 1，计算获得的摇滚减缩频率k=0.007 6，计算与试验获得摇滚频率较为接近。

图18 自由摇滚试验与计算结果对比（α=26°）Fig. 18 Comparison between wing rock experiment and CFD results （α=26°）

图19是Ma=0.6 时，在攻角α=22°，24.5°，26°下的单自由度运动特性曲线，左图是滚转角随时间的变化曲线，右图是相平面曲线，从图中可以看到，当攻角α=22°时，运动规律是收敛的，随着时间增加，滚转逐渐减弱，从相平面中也能够观察出这样的规律，当攻角α=24.5°，26°时，得到了典型的极限环运动，振荡平衡滚转角约为28°左右，振幅约为12°，计算获得的自由摇滚整体规律与风洞试验较为吻合。

飞翼标模动态失稳运动主要由模型在有滚转情况下，迎风侧与背风侧复杂流动相互作用诱导而成。其中迎风侧与背风侧定义为：当模型在有俯仰角的前提下，滚转角度为正时，在驾驶舱视角，右侧前缘为迎风侧，左侧前缘为背风侧。

图19Ma=0.6 单自由度自由滚转运动规律随攻角变化Fig. 19 Wing rock characteristics with angle of attack（Ma=0.6）

飞翼标模摇滚机理分析选用的典型工况为Ma=0.6、α=24.5°，选用如图19（b）红色方框中的一个周期来进行分析，此周期内振幅已较为稳定。图20 是自由摇滚过程中的空间流动变化，从图中可以看到，飞翼标模在背风侧一直保持着集中涡流动，同时在头尖处还会诱导一个较小的头部旋涡，在迎风侧则体现为较为复杂的大分离流动，其集中涡在靠近头部的位置就已经破裂。随着滚转角逐渐增加，背风一侧集中涡逐渐增强，涡轴逐渐向内侧移动，使得旋涡对飞翼标模的影响区域变大，而当滚转角逐渐变小，涡轴逐渐向外移动，体现出了周期性运动。在迎风侧，复杂的大分离流动体现为旋涡破裂后的螺旋波与高频小尺度涡，在滚转角较小时，高频小尺度涡离物面较近，诱导能力较强，随着滚转角逐渐增加，小尺度涡逐渐离开物面，旋涡诱导能力减弱。

图20 飞翼标模摇滚状态下非定常流动变化Fig. 20 Change of unsteady flow during wing rock of flying-wing

图21是亚声速（Ma=0.6，α=24.5°）滚转力矩随滚转角变化曲线，从图中可以看到，在一个振荡周期内，呈现出一个双“8”字环的特征，其中以滚转角28°为平衡位置，在滚转角22.5°～35°区间内，迟滞环为顺时针，整体效果为负阻尼效果，使得滚转运动处于发散状态，在滚转角16°～22.5°区间与35°～42.5°范围内，迟滞环为逆时针，整体效果为正阻尼效果，使得滚转运动处于收敛状态，顺时针迟滞环面积与逆时针迟滞环面积基本相等，使得飞翼标模能够在16°～42.5°范围内，呈现出周期性的极限环振荡运动规律。

图21 滚转力矩系数随滚转角变化Fig. 21 Roll moment coefficient with roll angle

对自由摇滚的流动机理分析主要可以从两个方面进行研究，一方面是横向静态特性，另一方面是横向动态效应。横向静态特性体现为，在自由摇滚范围内（图21），滚转力矩气动特征主要呈现静稳定特性，使得标模在自由摇滚过程中滚转角够回到平衡位置，此气动特性与三角翼摇滚较为一致。为了进一步分析自由摇滚流动机理，先分析静态特性对失稳运动的影响。

图22是不同滚转角下的横截面流线图与压力系数云图，截面位置为X=400 mm。选取的是在飞翼标模自由摇滚历程中所经历的3 个主要滚转角φ=20.4°，27.4°，38.5°。从图中也能够清晰的看到，飞翼标模横截面主要流动体现为左侧的集中涡流动与右侧的小尺度旋涡流动，随着滚转角的变化，两种流动也产生了相应的变化。图23是不同滚转角下的压力系数分布。图中显示，模型背风面的吸力整体量值较大，迎风面的量值较小，说明对于飞翼标模滚转力矩的影响主要来自于背风面，其中集中涡流动诱导正滚转力矩，分离流动诱导负滚转力矩。当φ=20.4°时，左侧集中涡产生的吸力峰值较大，右侧的旋涡分离流动吸力相对较小，所以对标模产生正向滚转力矩。随着滚转角逐渐增大，左侧集中涡位逐渐向内靠拢，涡吸力逐渐减小，当滚转达到φ=27.4°时，左右侧流动对滚转力矩的贡献较为接近，滚转力矩接近为0。当φ=38.5°时，集中涡诱导的吸力很小，此时分离流动诱导的负滚转力矩为主导，同时右侧迎风面也会出现压力峰值，所以整体产生负滚转力矩，通过以上3 个典型滚转角的分析能看到，飞翼标模体现出的滚转静稳定特性，主要为集中涡吸力诱导的正滚转力矩与分离流诱导的负滚转力矩随着滚转角变化相互“博弈”的结果。

图22 不同滚转角下的横截面流线Fig. 22 Streamlines of cross section at different roll angles

图23 不同滚转角下的横截面压力分布对比Fig. 23 Pressure distribution of cross section at different roll angles

横向动态效应体现为，在运动的过程中存在运动的迟滞效应（见图21 中的双“8”字迟滞环），使得飞翼标模能够在平衡位置附近（φ=28°）耗散能量，在双“8”字环的两侧积累能量，使得飞翼标模能够产生极限环振荡运动形式。以下分别选取双“8”字环中的“负阻尼”（φ=28°附近）与“正阻尼”（φ=38.5°附近）瞬时压力分布来分析流动对动态效应的贡献。 图24 为平衡位置附近（φ=28°）的运动历程放大图，其中有上行和下行两个过程，图25 的压力分布分别对应上行与下行运动经过φ=28°时的瞬时压力分布，图26 为上行与下行瞬时流动特性，从图中可以看到，当标模下行经过平衡位置（φ=28°）时，分离流动诱导的吸力较小，集中涡诱导的吸力较大，从而产生正向滚转力矩，当飞翼标模上行经过平衡位置（φ=28°）时，分离流诱导的吸力较大，同时集中涡诱导的吸力有减小的现象，从而诱导出负向滚转力矩。

图24 双“8”字环局部放大图（φ=28°附近）Fig. 24 Zoom-in view of double “8” ring （near φ=28°）

图25 上行与下行运动至φ=28°瞬时压力分布Fig. 25 Instantaneous pressure distribution when up and down motion to φ=28°

图26 上行与下行瞬时流动特性（φ=28°）Fig. 26 Transient flow characteristics of up and down motion （φ=28°）

图27为双“8”字环在滚转角φ=38.5°附近的局部放大图，图28 为上行与下行运动至滚转角φ=38.5°附近的压力分布对比情况，图29 为上行与下行瞬时流动特性。从图中可以看到，在上行与下行运动至φ=38.5°时，左侧集中涡变化不大，右侧分离流动在靠近边缘的地方有一定变化，在下行瞬时，分离流动诱导的吸力更大，并且在迎风侧也诱导出较大的正压力，二者均会诱导出负滚转力矩，所以下行瞬时会比上行瞬时诱导出更大的负滚转力矩。

图27 双“8”字环局部放大图（φ=38.5°附近）Fig. 27 Zoom-in view of double “8” ring （near φ =38.5°）

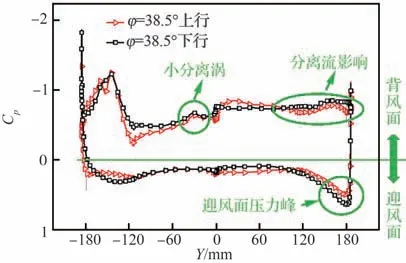
图28 上行与下行运动至φ=38.5°瞬时压力分布Fig. 28 Instantaneous pressure distribution when up and down motion to φ=38.5°

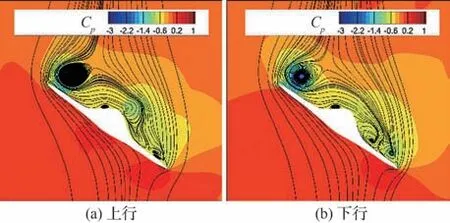
图29 上行与下行瞬时流动特性（φ=38.5°）Fig. 29 Transient flow characteristics of up and down motion （φ=38.5°）

7 飞翼标模横向失稳舵面控制特性

飞翼标模动态失稳是一个复杂的非线性现象，为了尝试探索飞翼标模自由摇滚的控制方法，采用偏转上扰流板、外侧副翼两种手段来模拟控制面固定舵偏对自由摇滚现象的控制效果。首先采用了上扰流板偏转方法，两侧上扰流板向上偏转30°，其物面网格与局部网格见图30。

图30 上扰流板偏转30°物面网格Fig. 30 Surface mesh of upper spoiler deflects by 30°

图31 是亚声速下自由摇滚上扰流板张开与无控状态下的对比情况，从图中可以看到，上扰流板张开之后，对于运动规律影响不大，在振幅上略有减小，在相平面中可以看到对于滚转角速度影响也较小。可见上扰流板在此工况下几乎无控制效果。图32 是上扰流板控制与无控状态下的频谱对比，图中显示上扰流板张开对于幅值有一定影响，但是对于自由摇滚频率影响微弱，并且依然存在机翼摇滚运动。

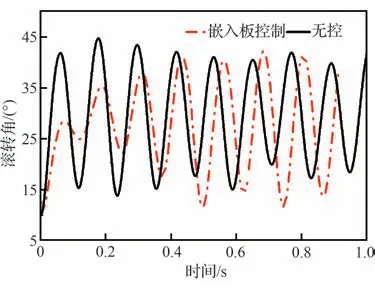
图31 自由摇滚上扰流板控制与无控状态对比Fig. 31 Upper spoiler control vs uncontrolled state in wing rock

图32 上扰流板与无控状态频谱对比Fig. 32 Spectrum comparison between upper spoiler and uncontrolled state

图33是外侧副翼偏转物面网格与局部网格，偏转方式为两侧副翼向下偏转30°。

图33 外侧副翼向下偏转30°物面网格Fig. 33 Surface mesh of outer aileron deflects downward 30°

图34为亚声速工况下，自由摇滚外侧副翼偏转控制效果，从图中可以看到，当外侧副翼向下偏转后，自由摇滚运动模式受到了很大的抑制效果，平衡位置从摇滚时的30°减小到25°左右，并且几乎不存在周期性振荡运动形式，外侧副翼向下偏转效果明显。

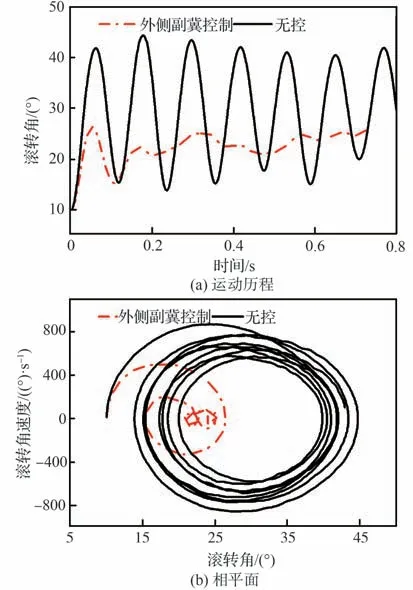
图34 自由摇滚外侧副翼与无控状态对比Fig. 34 Outer aileron vs uncontrolled state

8 结 论

采用非定常数值模拟DDES 方法模拟飞翼标模单自由度自由摇滚运动，并采用动力学模态分解（DMD）、物面脉动压力分析等方法分析飞翼标模非定常特性、自由摇滚机理，得到以下初步结论：

1）飞翼标模大攻角下非定常流动特性主要体现为，头部发展的集中涡、涡破裂、螺旋波流动结构，其中旋涡破裂点以St=0.12～0.23 的频率沿涡轴振荡，螺旋波频率在St=1.16～2.33 范围内。

2）飞翼标模亚声速自由摇滚现象平衡位置在滚转角28°，滚转角运动范围在16°～42.5°之间，在滚转角22.5°～35°区间内，阻尼整体效果为负阻尼效果，使得滚转运动处于发散状态，在滚转角16°～22.5°区间与35°～42.5°范围内，整体效果为正阻尼效果，使得滚转运动处于收敛状态。

3）自由摇滚现象的流动机理主要是背风侧的集中流动与迎风侧的具有较多小尺度旋涡的分离流动相互“博弈”。

4）上扰流板打开30°，对亚声速自由摇滚控制效果不明显，外侧副翼向下打开30°，能够在一定程度上抑制自由摇滚现象。