基于离散伴随的高超声速密切锥乘波体气动优化设计

刘超宇，屈峰，*，孙迪，刘传振，钱战森，白俊强

1．西北工业大学 航空学院，西安 710072

2．中国航天空气动力技术研究院，北京 100074

3．中国航空工业空气动力研究院，沈阳 110034

乘波体作为一种典型的高超声速飞行器构型，能够通过附着于前缘的激波将高压气流限制在飞行器下表面，在保证该区域流动均匀的同时可有效阻止溢流，从而实现较高的升阻比并便于实现机体与发动机的一体化设计［1-2］。因此，乘波体的研究受到了日益广泛的关注。传统的乘波体，如楔形流乘波体［3］、锥导乘波体［4］及密切锥乘波体［5］等，均是从已有的激波形状或流场出发，通过追踪流线生成乘波面。刘传振等［6-9］从密切锥方法出发，发展了定平面乘波体设计方法，提高了传统乘波体的设计灵活性和整体升阻特性。但是该类乘波体的设计方法是基于二维无黏理论推导出来的，因为忽略三维以及黏性效应，其在设计工况下仍会出现溢流，升阻比难以达到最优；另外，该类乘波体仍具有传统乘波体在偏离设计条件下，气动特性会出现恶化的不足［10］；同时，工程化的外形需要在理论模型的基础上实现头部/前缘钝化以及侧缘设计，而这些局部变化会对其气动特性产生较大的不利影响。因此，为使定平面形状的密切锥乘波体更具工程应用价值，有必要在考虑黏性的情况下，对其开展精细的气动优化设计［11］。

目前，国内外学者针对高超声速乘波体的优化 设计已开展了大量研究。例如：Rodi［12-13］采 用遗传算法和粒子群算法对相切流场乘波体的贝塞尔曲线前缘进行了优化设计研究；国内的张锋涛等［14］采用神经网络对乘波体进行优化，该方法在保证计算稳定的前提下有效提高了优化效率；徐佳胜［15］和吴功名［16］基于Kriging 代理模型方法分别对密切锥乘波体和类HTV-2 飞行器进行优化设计。但是，上述工作都是基于智能优化算法或代理模型方法进行的。这些优化方法在针对设计变量众多的乘波体三维整机开展气动优化设计时，会出现计算量过大的不足，一些情况下甚至可能得不到收敛结果［17-19］。与上述优化方法相比，基于伴随方程的梯度类优化设计方法可实现计算量与设计变量之间的基本解耦，并且精度较高，在大规模设计变量问题中优势明显［20］，比较适合于设计变量众多的高超声速乘波体整机气动外形优化设计。

一般来说，伴随类优化方法可分为连续伴随优化方法和离散伴随优化方法。而这2 类方法在高超声速气动优化设计中都得到了广泛的应用。连续伴随优化方法的研究方面，Kline 等［21］采用连续伴随方法针对高超声速进气道开展了优化研究；高昌等［22-23］通过建立基于连续伴随的优化方法，针对二维高超声速进气道和Sanger 飞行器机翼开展了优化设计研究。相较于连续伴随优化方法，离散伴随方程的优势为它与Navier-Stokes 方程的导数关系更清晰，实现起来比较方便且获取的梯度信息更为精确［24］。因此，诸多学者针对离散伴随方法在高超声速优化设计问题中的应用开展了研究。例如，Damm 等［25］基于离散伴随方法针对NASA P2 高超声速进气道开展了气动优化设计。高正红等［26］基于离散伴随方程法对某高超声速导弹的前体进行了气动外形优化。宋红超等［27］发展了基于离散伴随方法的高超声速单边膨胀喷管优化设计方法。但是，上述将伴随方法应用于高超声速优化问题中的工作多是针对飞行器局部简单部件开展优化设计的，缺乏在复杂飞行器整机气动优化设计当中的应用。另一方面，离散伴随优化多点设计的方式一般为加权平均，设计结果依赖于选取的权重系数，且需要进行多次尝试，而结构化网格求解器在相同资源条件下计算效率及精度更高［24］。因此，有必要实现基于结构网格数据结构的高超声速飞行器离散伴随气动优化设计方法。

针对上述问题，本文结合基于全速域通量求解方法和RANS（Reynolds Averaged Navier-Stokes equation）湍流模型的结构化网格求解器、鲁棒的结构网格变形方法、适用于高维设计变量的自由变形 （Free Form Deformation， FFD） 参数化方法、离散伴随方法与序列二次规划 （Sequential Quadratic Programming， SQP） 算法，实现了基于离散伴随的高超声速飞行器气动优化设计方法。基于该方法，针对定平面形状的密切锥乘波体构型分别开展了单一设计工况和多工况的三维整机气动优化设计。

1 基于离散伴随的高超声速飞行器气动优化设计方法

1.1 高超声速数值模拟方法

本文采用自主研发的高分辨率高超声速RANS 求解器针对高超声速流场开展数值模拟。该求解方法基于三维可压缩Navier-Stokes方程：

式中：q为流场守恒变量；f(q)表征无黏通量；fv(q)为黏性通量；Ω代表控制体；∂Ω为控制体边界；ΔSi为相应单元界面的面积。关于该控制方程的详细介绍，可参考文献［28］。

针对上述控制方程，采用基于格心的有限体积法构建了多块结构网格的流场求解器［29］。时间推进采用隐式LUSGS-GMRES（Lower Upper Symmetric Gauss Seidel-Generalized Minimum Residual）混合方法以保证定常流动求解的稳定性和收敛效率［30-31］。空间离散方法采用二阶MUSCL（Monotonic Upstream-centered Scheme for Conservation Laws）重构方法以及minmod 限制器［32］，通量求解方法采用适用于全速域流动计算的HLLEMS（modified HLLE scheme with a switch function）格式［33］。湍流模型采用一方程SA 模型［34］。为了提高求解效率，该求解器采用了MPI（Message Passing Interface）并行和多重网格技术。

1.2 离散伴随梯度求解方法

采用离散伴随方程法求解梯度是本文所实现的高超声速飞行器气动优化设计平台的核心。离散伴随方程法首先对非线性化的偏微分流动控制方程进行离散，然后对其进行线性化，最后通过离散形式的线化控制方程，推导出离散伴随方程及其边界条件。如果伴随方程的形式和原始流场控制方程的离散形式完全对应，则可以求解出目标函数和控制方程离散形式的精确导数［35］。相比于连续伴随方程法，离散伴随方程法得到的梯度往往更接近真实值，可以同时用于自适应网格生成和误差分析［36］。因此，本文采用离散伴随方法对气动目标函数的梯度进行求解。

假设气动优化目标函数为F(G(x)，Q(x))，其中：x为设计变量，表征FFD 方法中各个控制点的位移；G(x)为由设计变量x所确定的 CFD计算网格，包括表面网格Gs和空间网格Gv；Q为流场解向量。通过FFD 外形参数化，可由设计变量x获得表面网格Gs(x)，再由网格变形法获得空间网格Gv(x)。在给定一组设计变量x的情况下，通过求解式（2）便可得到相应的一组空间流场解Q。

式中：R为流场控制方程的残差，对于收敛的定常流场，可认为控制方程的残差近似为0。

将F、R分别对设计变量x求全导数，则有

式中：dQdx为空间流场解对设计变量的全导数。若采用传统的梯度求解方法求解，需对x的每一个分量进行扰动，然后分别求解流场控制方程。在设计变量较多时，计算量毫无疑问是巨大的。为了提高求解效率，将式（4）作恒等变换为

将式（5）代入式（3）可得

则可以将矩阵求逆转化为求解线性方程组，即转化为求解伴随变量：

此时，式（6）可以写为

式中：∂F∂G只需要在收敛的流场上对网格变量求偏导数即可；dGdx为空间网格对设计变量的导数，通过网格变形算法确定；∂R∂G为流场残差对于空间网格的偏导数，在流场计算中可求得此项，计算量也相对较小。因此准确高效求解式（9）主要体现在偏导数矩阵的获取以及伴随方程式的求解。偏导数矩阵的获取通过自动微分技术来实现，具体可参考文献［37］；伴随方程式（8）本质上是一个大规模、高度稀疏的线性方程组，采用广义最小残量（Generalized Minimum Residual， GMRES）算法来对其进行求解［30］。

1.3 气动优化设计平台

基于1.1 节所述的高精度RANS 流场求解器，通过结合适用于高维的FFD 参数化方法［38］、鲁棒的结构网格变形方法［39-40］、离散伴随方法和SQP 算法［41］，构建了基于离散伴随的高超声速飞行器气动优化设计平台，其流程图如图1所示。

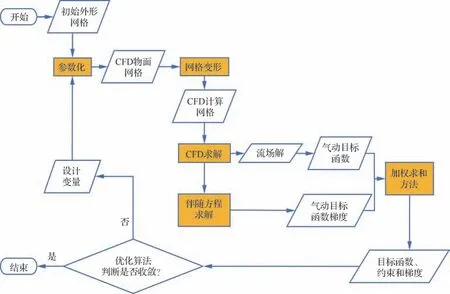
图1 基于离散伴随的高超声速飞行器气动优化设计方法流程图Fig. 1 Flow chart of aerodynamic shape optimization design software for hypersonic vehicle based on discretized adjoint method

首先，基于高超声速飞行器初始外形生成用于CFD 计算的空间网格，并从空间网格中提取出目标表面网格。其次，根据优化的问题建立包裹飞行器外形的FFD 控制体，将控制体上的坐标点位移作为外形设计变量。对控制体坐标点进行扰动之后，输出新外形的表面网格。表面网格进一步传递至网格变形模块，根据逆距离权重插值算法实现了空间网格的变形更新，生成了新的空间计算网格。随后，对于新的空间网格进行高精度CFD 流场计算，得到收敛的流场解向量以及气动目标函数的值。根据收敛的流场解向量构造伴随方程，求解伴随方程获得目标函数相对于设计变量的梯度。对于多目标优化问题，采用加权平均方法将多目标优化问题转化为单目标优化问题。不同权重系数的设置能够改变优化的侧重点，以达到期望的优化结果。最后，目标函数以及它们对应的梯度一起反馈给优化算法，判断是否满足优化收敛准则。若不满足，优化算法SQP 将计算搜索方向和步长，获得新的设计变量，进行下一步迭代，如此循环直至优化迭代收敛。

2 高超声速定平面密切锥乘波体

选取基于定平面形状方法设计得到的密切锥乘波体作为初始构型［6-8］。图2 为该乘波体全模的几何外形，图3 为乘波体半模的几何尺寸，其中：X轴为流向，Y轴为升力 向，Z轴为展向。该构型的平面形状为小弯头单后掠，后掠角为75°，并通过前缘钝化、上表面容积扩充、增加后体等方法将其工程化。通常，前缘钝化处理有2 种方式：① 根据钝化半径，对前缘上下表面进行修形；② 下表面前缘不变，整体上移上表面直到满足钝化半径［42-43］。本文采用第1 种方式对乘波体前缘进行钝化处理，钝化半径为 2 cm。由于定平面密切锥乘波体在设计时未考虑底阻的影响，本文为研究三维黏性效应以及工程化处理对乘波体升阻特性的影响，将在优化设计时基于分部件积分并扣除掉底阻。本文所选取的乘波体初始构型的设计工况为：马赫数Ma=5，迎角α=6°。

图2 乘波体初始构型Fig. 2 Initial model for waverider

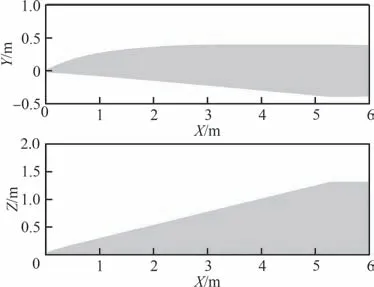
图3 乘波体平面尺寸Fig. 3 Plane size for waverider

采用粗、中、细3 套网格对本文所选用的定平面密切锥乘波体进行网格无关性验证，网格量分别为212 万、403 万和801 万。表1 给出了在密切锥乘波体设计状态下的网格无关性验证结果，表中CL、CD分别为升力系数和阻力系数；图4 给出了3 种网格在对称面处压力系数（Cp）对比。可以看到，3 种网格的阻力系数CD的计算结果相差较小，因此，为保证优化设计过程中的计算精度和计算效率，本文选用中等网格进行后面的气动优化设计。

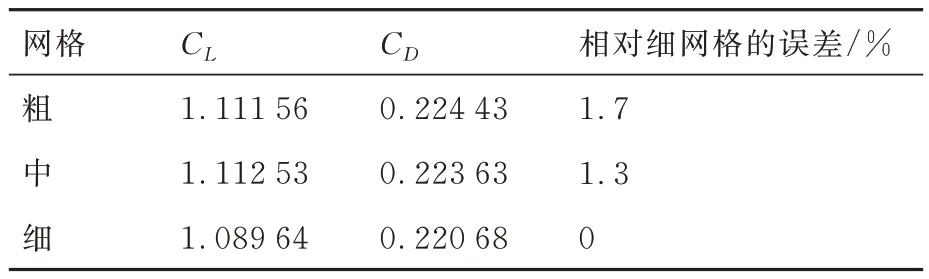
表1 乘波体网格无关性验证结果Table 1 Grid independent compute results of waverider

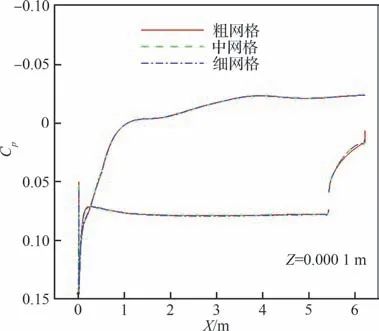
图4 对称面处表面压力系数对比Fig. 4 Comparison of surface pressure coefficient on plane of symmetry

3 离散伴随方法精度验证

在开展气动优化设计之前，采用离散伴随方法针对密切锥乘波体进行梯度求解，对伴随方法求解结果进行计算精度的验证。图5 给出了乘波体的FFD 控制框。该控制框采用20 个控制剖面，每个控制剖面沿弦向上下表面各有17 个控制点，共34 个控制点。每个控制点只能在Y向移动，用来对乘波体型面进行扰动。另外，为了保持前后缘线为直线，每个控制剖面上下表面沿弦向第一个和最后一个点保持不动。因此共有600 个FFD 控制点位移设计变量。

图5 密切锥乘波体FFD 控制框Fig. 5 FFD box of osculating-cone waverider

对FFD 控制点进行扰动，并分别用有限差分法和离散伴随方程法计算各气动力系数相对于设计变量的偏导数，计算过程中差分步长选取1×10-4、1×10-5和1×10-6。采用一组随机数选取15 个FFD 控制点的计算结果，图6 给出了2 种方法的计算结果对比，其中，Xi为随机选取的第i个设计变量，CMZ为俯仰力矩系数。可以看出有限差分法（Finite Difference method， FD）和伴随方程法的计算结果吻合较好，说明伴随方程法在求解梯度时具有较高的计算精度。

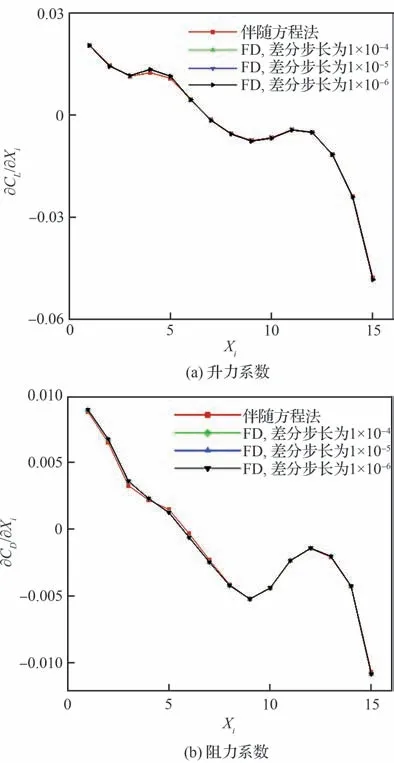
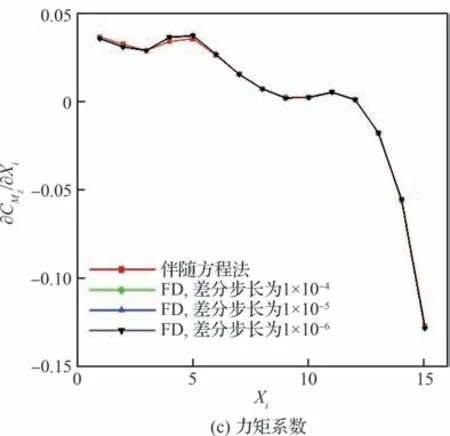
图6 伴随方程法和有限差分法计算结果对比Fig. 6 Comparison of computed results between adjoint method and finite difference method

4 高超声速乘波体气动优化设计

基于第1 节实现的高超声速飞行器离散伴随气动优化设计方法，本节针对定平面形状的密切锥乘波体构型分别开展了设计工况下的三维整机气动优化设计以及包含非设计点的多工况气动优化设计。

4.1 单点优化

单点优化设计选取初始构型的设计工况，即Ma=5，高度H=34 km，α=6°。目标函数及设计约束为

式中：CL为升力系数；CD为阻力系数；CD0为初始阻力系数；ti0为初始构型第i个站位处的厚度；ti为优化后构型第i个站位处的厚度；V为优化构型体积；V0为初始构型体积。该算例的设计目标为升阻比最大，而设计约束为：飞行器阻力值不超过初始值、厚度不小于初始的95%、容积不降低。

计算效率方面，本文基于MPI 并行方法在56核CPU 下开展整机单点优化设计，并仅耗时约27 h 即完成13 次梯度优化迭代以及59 次流场求解，进而得到了收敛的优化构型。相较于初始构型，单点优化构型满足厚度约束且其容积保持基本不变。

表2 对比了优化前后不同构型的升阻力特性，其中：CDp表征压差阻力系数；CDf为摩擦阻力系数；CL CD为升阻比。可以看出，本文优化得到的构型可以显著改善飞行器的升阻特性，优化后飞行器升阻比提升了4.9%。

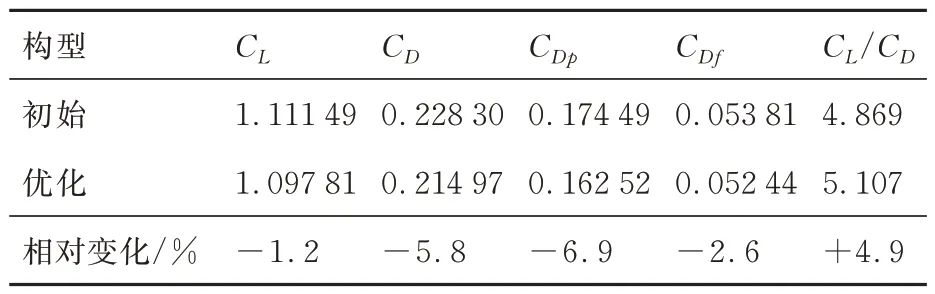
表2 优化前后升阻力特性对比（单点优化）Table 2 Comparison of lift and drag characteristics before and after optimization （single point optimization）

表3 给出了单点优化前后压心xcp位置的变化情况。其中：xcp为纵向压心位置，即压心距头部的距离占全机长度的比例。可以看出，单点优化构型的压心位置无明显变化。

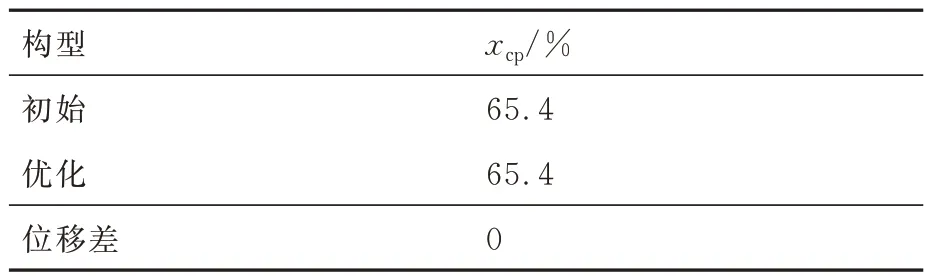
表3 优化前后压心位置对比（单点优化）Table 3 Comparison of pressure center positions before and after optimization （single point optimization）

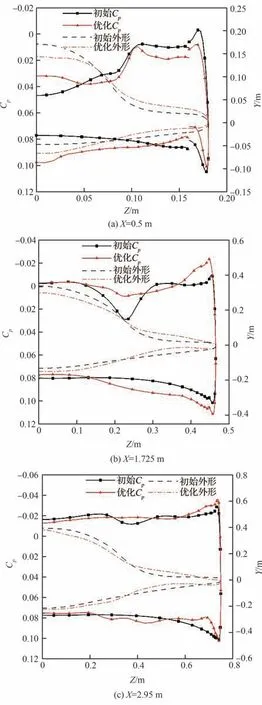
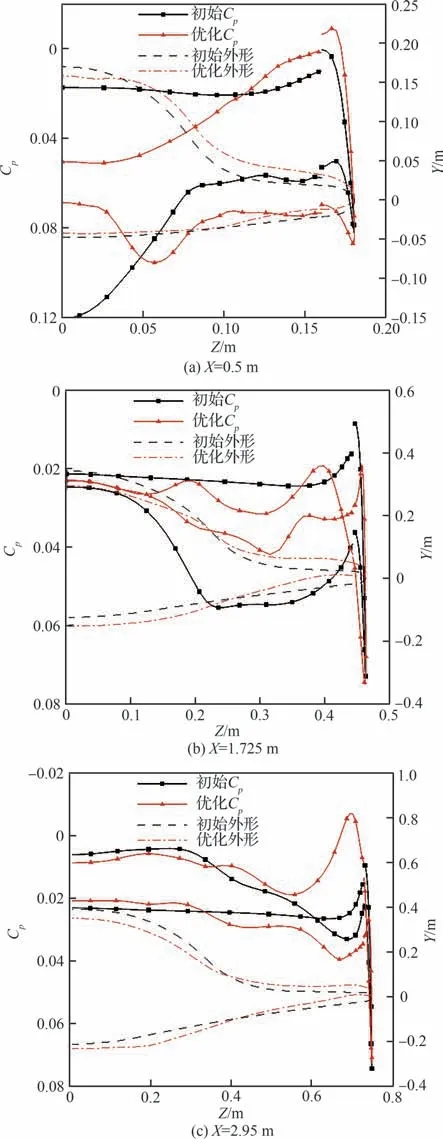
图7 和图8 给出了初始外形和优化后外形的空间流场及压力系数云图对比。图9 为选取的乘波体5 个站位示意图。图10 给出了乘波体在不同站位处的外形变化和表面压力系数分布对比。可以看出，初始外形在头部隆起，使得气流在背风面的流动会受到压缩进而产生激波，激波后的头部背风面处会有局部高压区。而优化后的外形在头部隆起的部位变得更加平缓，使得背风面激波强度减弱，激波相对上移，波后压力减小。初始外形迎风面激波依附在前缘，流场较均匀。优化后外形在头部下表面（靠近对称面处）下凸，物面角增大，激波强度更强，在波后出现局部高压区，使得头部处升力增大。因初始外形前缘进行钝化处理，在进行黏性计算后前缘处会出现溢流，迎风面高压气流转移到背风面，使得背风面前缘处的低压区减小，导致气动性能的损失。优化后的外形则对背风面前缘附近的溢流有所抑制。

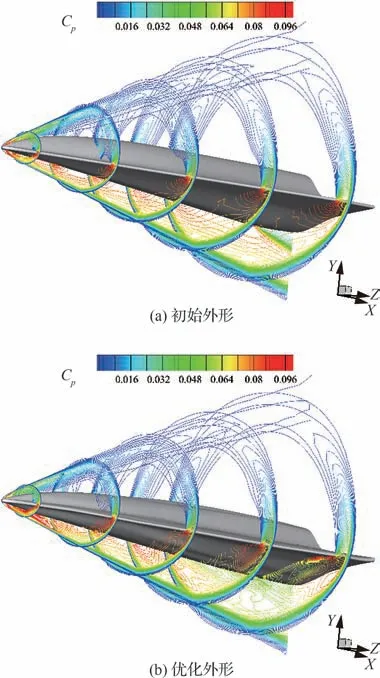
图7 优化前后空间流场对比（单点优化）Fig. 7 Comparison of flow field of waverider before and after optimization（single point optimization）

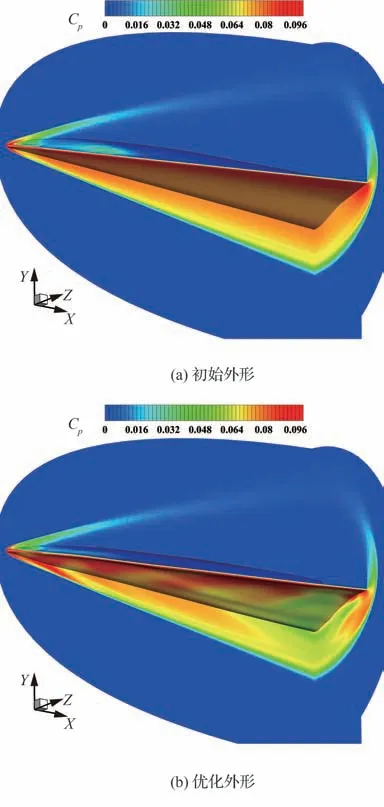
图8 优化前后压力系数云图对比（单点优化）Fig. 8 Comparison of pressure coefficient contours before and after optimization （single point optimization）

图9 乘波体5 个站位Fig. 9 Five stations of waverider configuration

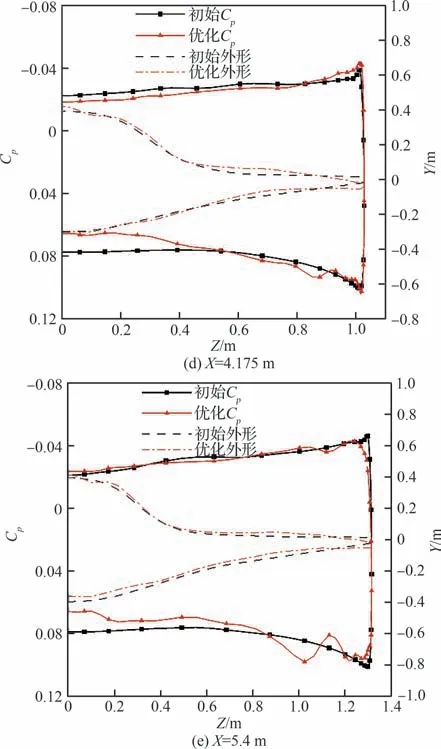
图10 优化前后各截面外形和表面压力系数分布对比（单点优化）Fig. 10 Comparison of sectional shapes and surface pressure coefficient distributions before and after optimization（single point optimization）

在乘波体的中后部，优化前后外形在背风面压力变化较小，优化后外形在类似于翼身过渡处略微上凸，相应处的压力也会较大。而优化后外形的下表面相对上移，气流流经物面的物面角减小，激波相对下移，且激波强度减弱，导致波后的压力也会更小。由于乘波体中后部的面积较大，这也使得优化后外形整体的升力有所下降。但是，由于激波强度的减弱，波阻也会更小，从而使得优化后外形阻力明显下降。另外，优化后外形在前缘处相对下偏，表面压力波动较大，在一定程度上限制了迎风面附近的高压气流。

4.2 多点优化

本节选取如下状态开展多点气动优化设计：Ma=5，H=34 km，αn(n=1，2，3)。其中，非设计状态为α1=0°和α2=2°，设计状态为α3=6°。目标函数及设计约束为

式中：CL0为初始升力系数。

多点优化问题的目标函数为各迎角状态下升阻比的线性加权和。其中，权重系数按照各迎角状态下初始升阻比的比例，分别取为ε1=0.1、ε2=0.4、ε3=0.5。多点优化设计的约束为：各迎角状态升力值不低于初始值、阻力值不超过初始值、几何约束为厚度不小于初始的95%、容积不降低。

计算效率方面，基于MPI 并行方法在56 核CPU 下开展整机多点优化设计，仅耗时约60 h 即完成9 次梯度优化迭代以及93 次流场求解，进而得到了收敛的优化构型。相较于初始构型，多点优化构型也满足厚度约束且其容积保持基本不变。图11 给出了多点优化迭代收敛历史，图中L/D为升阻比。在优化的前20 步主迭代内，各迎角状态的升力系数和升阻比提升明显，非设计状态阻力系数有不同程度的下降，在设计状态6°迎角阻力系数有小幅提升。20 步之后，各气动参数变化趋于平缓。

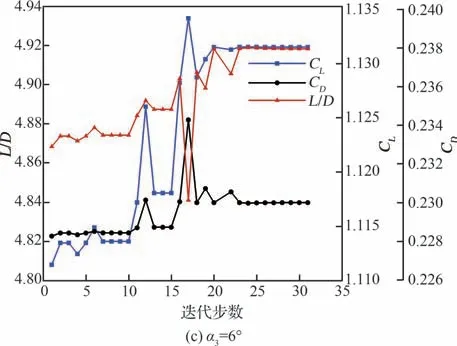
图11 多点优化迭代收敛历史Fig. 11 Convergence history of multi-point optimization iterations

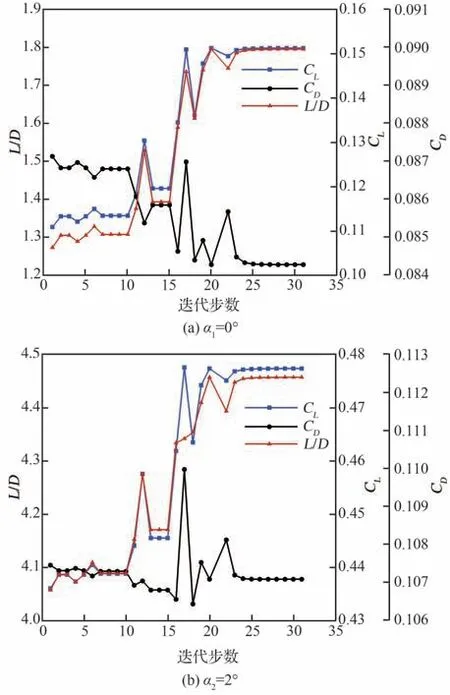
表4 对比了多点优化前后不同状态升阻力特性。可以看出，非设计迎角状态的升阻比明显增大。优化效果的来源主要为升力的大幅增加，同时阻力有所降低；在设计状态升阻比小幅提升，阻力略有升高。相对于初始外形，气动优化得到的外形可以保证设计状态升阻比不下降的同时，显著提升非设计状态的整机升阻特性。

表4 优化前后升阻力特性对比（多点优化）Table 4 Comparison of lift and drag characteristics before and after optimization （multi-point optimization）

表5 给出了多点优化前后压心xcp位置的变化情况。其中，CM为俯仰力矩系数的绝对值，力矩参考点为机头对应的坐标。可以看出，相较于初始构型，多点优化构型在各迎角下的压心位置均有所前移。在非设计0°迎角状态，压心变化幅度较大，原因可能是在0°迎角下，俯仰力矩系数绝对值较小，压心位置对气动外形变化的敏感度较大。另外，本文选取研究对象是定平面形状密切锥乘波体，并未添加平垂尾、V 尾等气动控制部件，因此压心变化幅度较大。

表5 优化前后压心位置对比（多点优化）Table 5 Comparison of pressure center positions before and after optimization （multi-point optimization）

图12 展示了优化前后外形变化情况，其中，灰白色为初始外形，蓝色为优化外形，5 个典型站位中黑色实线为初始外形的截面曲线，红色实线为优化外形的截面曲线。图13～图16 给出了初始外形和优化后外形在2 个非设计迎角状态下的空间流场及压力系数云图对比。图17 和图18 给出了乘波体在2 个非设计迎角状态下各站位处的外形变化和表面压力系数分布对比。与单点优化类似，优化后的外形在头部隆起的部位变得更加平缓，使得背风面激波强度减弱，激波相对上移，波后压力减小，这在非设计状态优化前后的流场对比中可以明显看出。初始外形下表面激波依附在前缘，流场较均匀。优化后外形在头部下表面（靠近对称面处）因型面的变化产生二次激波，在波后出现局部高压区，使得头部处升力增大。但相较于下压缩面，上表面的型面变化导致优化外形对来流的压缩减弱，背风面压力明显下降，因此其对非设计迎角状态下的气动性能产生主要的影响。因初始外形前缘进行钝化处理，在进行黏性计算后前缘处会出现不同程度的溢流，在非设计状态处溢流较为明显，迎风面高压气流转移到背风面，使得背风面前缘处的低压区减小，导致气动性能的损失。而优化后的外形显著抑制了背风面前缘附近的溢流量，特别是在2°迎角时，高压气流能更好地被限制在前缘下表面。

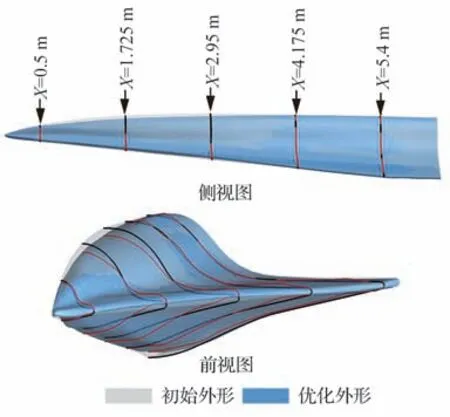
图12 优化前后外形比较Fig. 12 Comparison of waverider shape before and after optimization

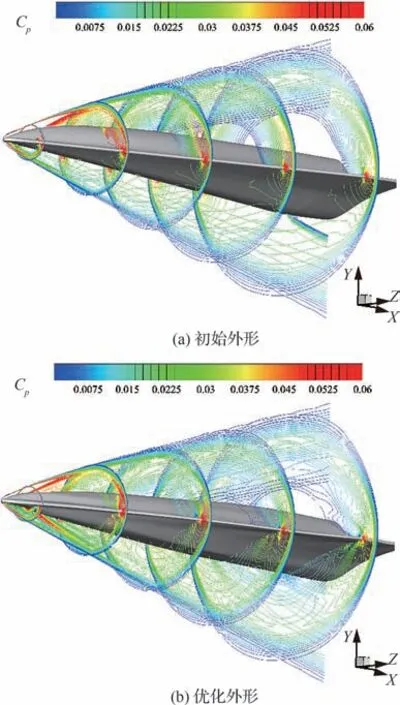
图13 非设计状态α1=0°优化前后空间流场对比Fig. 13 Comparison of flow field of waverider before and after optimization at non-design state with α1=0°

图14 非设计状态α1=0°优化前后压力系数云图对比Fig. 14 Comparison of pressure coefficient contours before and after optimization at non-design state with α1=0°

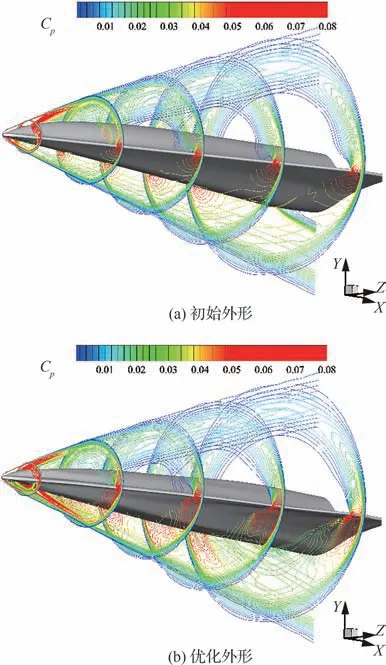
图15 非设计状态α2=2°优化前后空间流场对比Fig. 15 Comparison of flow field of waverider before and after optimization at non-design state with α2=2°

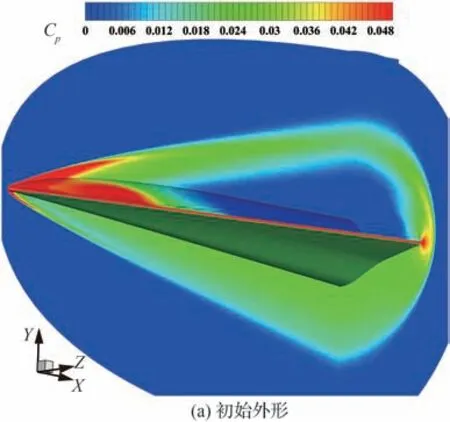
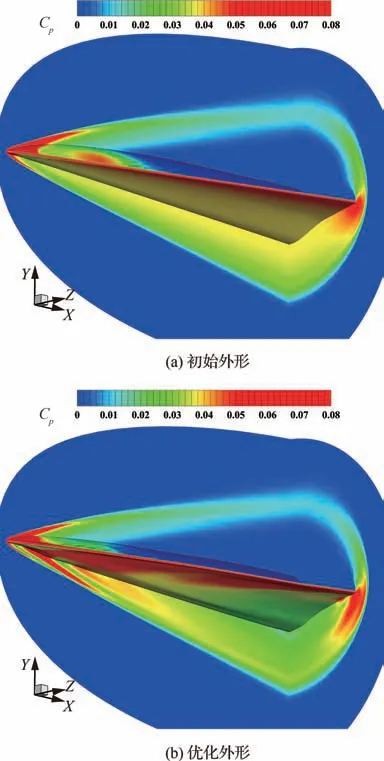
图16 非设计状态α2=2°优化前后压力系数云图对比Fig. 16 Comparison of pressure coefficient contours before and after optimization at non-design state with α2=2°

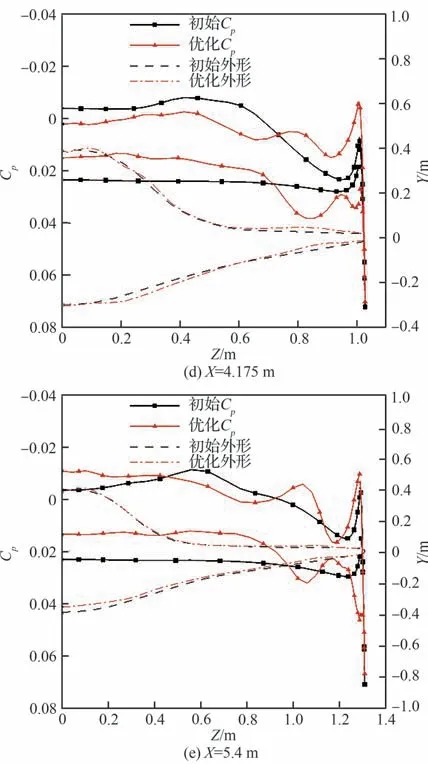
图17 优化前后各截面外形和表面压力系数分布对比（α1=0°）Fig. 17 Comparison of sectional shapes and surface pressure coefficient distributions before and after optimization （α1=0°）

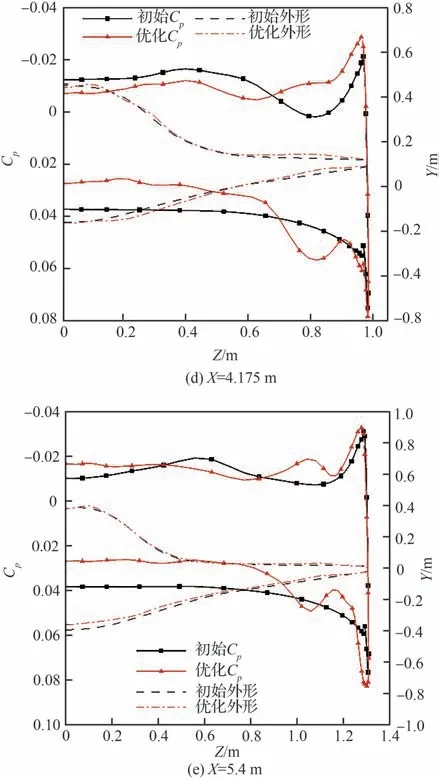
图18 优化前后各截面外形和表面压力系数分布对比（α2=2°）Fig. 18 Comparison of sectional shapes and surface pressure coefficient distributions before and after optimization （α2=2°）

在乘波体的中后部，优化后外形在中部前缘明显上凸，激波后的气流流经背风面又产生一道膨胀波，且相对于初始外形，膨胀波前移，波后气流加速，因此中后部背风面的压力更小。相应的，优化后外形上表面（靠近前缘处）也略微上移，激波强度相对更强，波后速度更小，升力更大，这也是升力增量的主要来源。此外，优化后外形下表面（靠近对称面处）相对上移，气流流经物面的物面角减小，激波相对下移，且激波强度减弱，导致波后的压力略有减小，这使得波阻有所下降。

综上所述，在非设计状态下优化后外形背风面压力下降，迎风面压力增加，同时优化后的前缘外形能更好地将高压气流限制在迎风面。因此，优化后外形非设计状态下的升阻比提升明显。

图19 和图20 给出了初始外形和优化后外形在设计状态6°迎角的空间流场及压力系数云图对比。图21 给出了乘波体在设计迎角状态下各站位处的外形变化和表面压力系数分布对比。与单点优化不同的是，优化后外形在头部下表面（靠近对称面处）先相对上移，而后又下凸，产生二次激波，在波后出现局部高压区，头部处压力相对单点优化外形更大；另外，通过空间流场对比和表面压力系数分布对比也可以看出，多点优化后的外形能够更好地阻止前缘迎风面的高压气流泄漏到背风面。在乘波体的中后部，与单点优化不同的是，优化后外形在中后部前缘更加上翘，激波强度相对更强，波后速度更小，因此前缘处的背风面压力更小，迎风面压力更大；但相应的波阻也会增加，因此阻力也相对更大。

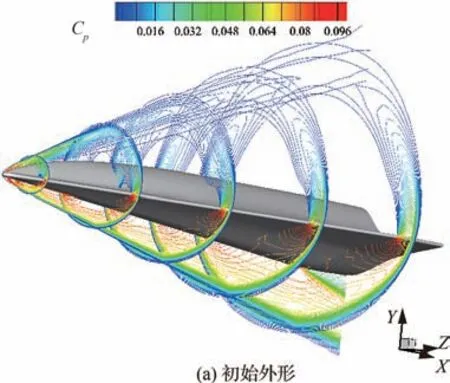
图19 设计状态α3=6°优化前后空间流场对比Fig. 19 Comparison of flow field of waverider before and after optimization at design state with α3=6°

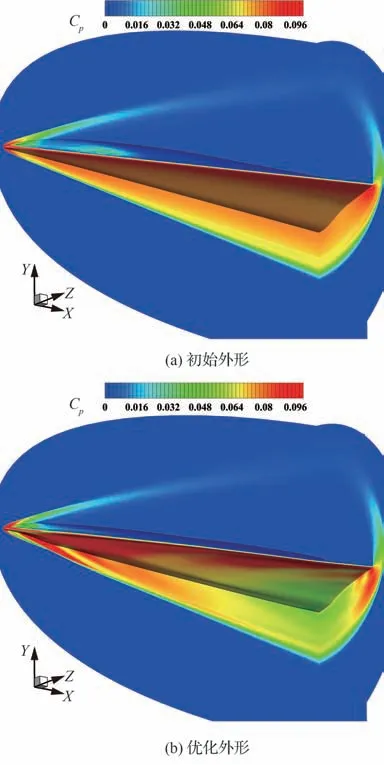
图20 设计状态α3=6°优化前后压力系数云图对比Fig. 20 Comparison of pressure coefficient contours before and after optimization at design state with α3=6°

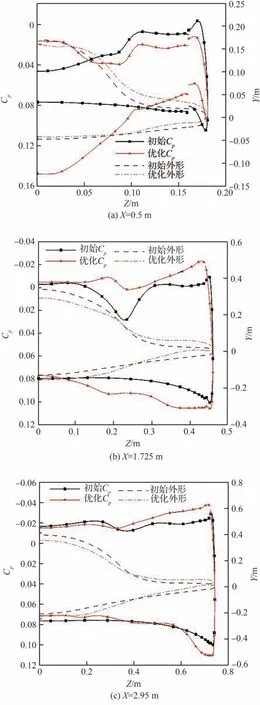
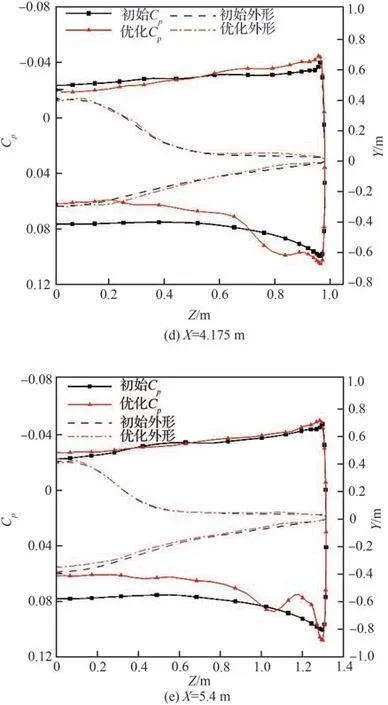
图21 优化前后各截面外形和表面压力系数分布对比（α3=6°）Fig. 21 Comparison of sectional shapes and surface pressure coefficient distributions before and after optimization （α3=6°）

综上所述，相对于单点优化外形，多点优化后的外形在设计状态下头部和前缘处的压力分布明显改善，同时优化后的前缘外形能更好地将高压气流限制在迎风面。但是因为波阻的增加，阻力相对更大。因此，多点优化时飞行器在设计状态下的升阻比提升幅度较小。

5 结 论

1）本文通过结合RANS 求解方法、结构网格变形方法、FFD 外形参数化方法、离散伴随方法与序列二次规划算法，实现了基于离散伴随的高超声速飞行器气动优化设计方法。

2）定平面密切锥乘波体的梯度计算结果表明，本文所采用的离散伴随方程法具有较高的梯度求解精度。针对定平面形状的密切锥乘波体的气动优化设计表明，本文所采用的基于离散伴随的优化设计方法在针对大规模设计变量的高超声速飞行器开展气动优化时具有较高的优化效率，具体为：在400 万多块结构网格、600 个设计变量以及303 个设计约束条件下，该方法仅分别花费2 240CPU 小时和3 360CPU 小时即完成单一设计状态和多工况的整机气动优化设计。

3）定平面密切锥乘波体在单设计点优化后，阻力下降明显，升阻比提升了近5%；在多点优化设计后，可以保证各个飞行状态下的气动性能均有所提升，具体为：多点优化得到的构型在保证设计点状态升阻特性不下降的同时，将非设计点的升阻比提升10%以上。

4）本文所实现的气动优化设计方法在一定程度上改善了定平面密切锥乘波体的理论局限性，并在工程化外形整机气动优化设计中展现出良好的优化性能。