基于梯度下降的水滴收集率计算方法

任靖豪，王强，2，李维浩，刘宇，易贤，2，*

1．中国空气动力研究与发展中心 结冰与防除冰重点实验室，绵阳 621000

2．中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000

飞机结冰数值计算中，水滴收集率的计算方法分为两类：欧拉方法［1-3］和拉格朗日方法。拉格朗日方法通过求解水滴运动方程，分析单颗水滴的运动轨迹，进而获取液滴的撞击特性。由于其算法简单，计算过程表征直观，且在描述过冷大水滴（SLD）动力学特性［4-5］方面具有天然优势，被广泛应用于结冰数值仿真［6-8］。在二维和简单三维外形问题上，展现出了高效的计算优势。然而，针对三维复杂构型问题，由于水滴轨迹计算量大、收集率计算复杂，制约了拉格朗日方法的发展。

近些年，国内外的研究者也在不断挖掘拉格朗日方法的计算潜力。其中Lee 等［9］利用高斯形函数发展了一种基于粒子统计的数值计算方法，并将该方法应用于发动机叶片的三维水滴撞击特性研究中。文献［10］在此基础上结合离散随机步模型，实现了考虑湍流影响的水滴运动过程模拟。为了进一步适应较大规模的水滴轨迹跟踪计算，Rendall 等［11］发展了一种水滴运动方程的隐式计算方法，显著提高了拉格朗日水滴轨迹方程的求解效率。文献［12-13］基于拉格朗日流管法，利用网格加密的方式，自适应地控制关键区域的水滴释放密度。相比统计法，该方法极大地降低了水滴轨迹计算规模。文献［13］还提出了一种限制径向基函数插值方法，用于改善撞击点向物面网格点传递水滴收集率的鲁棒性。笔者团队在此基础上发展了一种壁面投影算法［14］，改进了拉格朗日轨迹法对迎风区和背风区的辨识能力，实现了三维复杂构型的水滴收集率快速计算。但是上述拉格朗日流管法需要依赖插值技术将水滴收集率传递到网格角点。其中插值精度很大程度上受撞击点分布特性的影响。当撞击点分布不均匀或样本较少时，计算结果的可靠性会随之下降。

为了克服插值带来的不利影响，本文提出了一种基于梯度下降模型［15］的水滴收集率计算方法。文中采用该方法开展了三维圆球、30P30N 平直多段翼、ONERA-M6 机翼和某型发动机短舱等典型外形的水滴收集率计算，并分别与文献试验数据和计算结果进行对比分析，用于验证改进方法的可行性。

1 液滴撞击特性计算方法

1.1 流场计算

水滴撞击特性计算分为两步：①首先采用欧拉方法求解空气流场；②基于空气流场结果开展水滴轨迹计算，进而获得水滴收集率。本文采用中国空气动力研究与发展中心自研的PHengLei求解器［16］开展流场计算。

1.2 水滴运动方程及其求解方法

求解的水滴轨迹方程满足以下几个假设条件：

1） 水滴运动过程中仅受自身重力、流场的黏性阻力和浮力，且不考虑液滴对空气流场的影响。

2） 采用球形阻力公式计算液滴所受阻力，且期间不考虑液滴变形、破裂、凝聚等动力学特性。

3） 液滴运动过程中不考虑质量损失。

根据牛顿第二定律，液滴运动的控制方程表达式为

式中：ua和ud分别表示当地背景流场速度和液滴的运动速度；ρd和ρa分别为液滴和空气的密度；g为重力加速度；f为液滴的弛豫系数，其表达式为

其 中：μ为空 气黏性系数；d为液滴 粒径；CD为 液滴阻力系数；Re为液滴运动的相对雷诺数；组合参数CD·Re/24 的表达式为

式（1）为求解一阶常微分方程的初值问题。通过给定水滴初始位置和速度条件，采用四阶Runge-Kutta 方法［17］对式（1）进行数值积分，求得水滴的运动轨迹。

式中：r为水滴位置坐标；下标0 表示水滴初始参数；rp为水滴颗粒空间坐标。

1.3 液滴定位及流场参数插值

求解水滴运动方程过程中，每个时间步都需要更新水滴所受的气动力。因此需要明确各时刻水滴颗粒所处网格单元的编号，通过插值得到液滴当地位置的空气流场信息。

采用定向查找算法［14］，以最优路径快速定位出液滴所处单元。明确了水滴所处网格单元后，采用径向基函数（RBF）插值方法［18］计算水滴所处位置的流场参数值。该插值方法的优势在于插值精度高，且外插结果具有较好的连续性。

径向基函数的基本表达式为

式中：n为样本点个数；rtar和ri分别表示插值目标点和第i个样本点在变量空间中的坐标；ωi为第i个样本点的插值权重系数；φ（r）为径向基函数；R为基函数的支撑半径。选用Wendlend’s C2 函数作为基函数，表达式为

将粒子当前所处的网格单元角点作为插值样本S=｛r1，r2，…，rn｝，Sv=｛q1，q2，…，qn｝，通过式（8）求解各样本点的插值权重。

得到权重系数矩阵W后，代入式（5）估算出当前位置的流场信息。

如图1 所示，在近壁面长宽比较大的网格内进行插值时，数值误差易造成径向基函数矩阵为奇异矩阵。因此，需要将样本点变量空间坐标进行无量纲化，消除变量量纲对插值结果的影响。

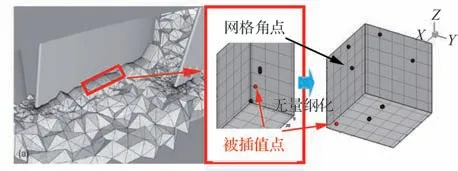
图1 无量纲化示意图Fig. 1 Dimensionless processing

1.4 水滴收集率计算

液滴收集率的定义：单位时间内，壁面与自由来流处单位面积上水滴的质量通量的比值，表达式为

式中：为单位时间流过面元A的液态水质量。当液滴轨迹不发生交叉时，可用多条相邻轨迹组成的“流管”描述该区域内所有水滴的运动特性。式（10）可以改写成如下形式：

式中：n为流管内的水滴个数；md，i为编号i的液滴质量。若水滴发生交叉，并在物面上表现出不同流管的撞击域发生重叠，采用面积比率的计算方式易低估水滴收集率。此时，通常采用时均统计的方法，对撞击特性进行分析。

2 基于梯度下降模型的收集率计算

当水滴撞击点与网格角点一致时，可直接计算物面网格面心上的水滴收集率，计算结果不受插值精度影响。基于这一思路，建立水滴撞击准确度的评价函数F。将水滴释放点坐标作为函数输入，撞击点到目标角点距离作为函数输出。采用梯度下降法沿函数梯度下降方向求解极小值点，即可得到一条逼近目标角点的水滴轨迹。

2.1 水滴轨迹的邻域模型

引入方形邻域模型，通过在水滴释放点P邻近区域增加额外的水滴轨迹信息辅助求解函数的偏导数。图2中δ表示邻域尺度，黄色单元格为辅助水滴的释放位置，其中辅助水滴粒径可能大于邻域尺度。在获取模型各水滴撞击点与目标点的距离值后，通过差分或最小二乘法计算P点处函数梯度值。

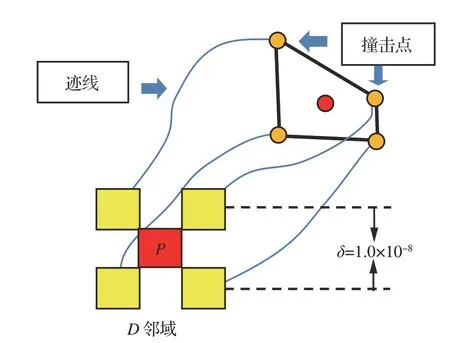
图2 水滴轨迹邻域示意图Fig. 2 Neighborhood model of droplet trajectory

为保证背景流场参数插值结果有较好的连续性，该邻域模型内的5 颗水滴质点需采用相同的插值样本，即对这5 颗水滴进行同步追踪并默认其位于同一网格单元内。

2.2 计算方法

已知有一条水滴轨迹trai撞壁，其撞壁信息包含：撞击点位置、释放点位置、撞击点所处的壁面网格单元编号。选取trai撞击的壁面网格单元上某角点作为目标点。将trai释放点坐标xi作为函数F的输入，trai撞击点到目标点的距离si作为函数F的输出，即

由于在拉格朗日算法中水滴通常释放于垂直来流的某一空间平面上，即xi是一组平面正交基表示的二维矢量，其矩阵形式可写成xi［u，v］。

采用2.1 节介绍的水滴邻域模型，可以额外获得4 个撞击点信息。通过最小二乘法求解方程组（13）：

式中：

两特征方向的偏导数可表示为

式（14）中Δulm=ul-um，邻域模型中心点编号为0，其他点编号分别为1，2，3，4。

求得梯度后，采用递归式（16），调整水滴释放点位置重新计算水滴轨迹，并带回函数（13）重复上述步骤直至函数值小于给定阈值，式（16）中g（xik）表示水滴释放位置修正的位移量，计算示意图如图3 所示。

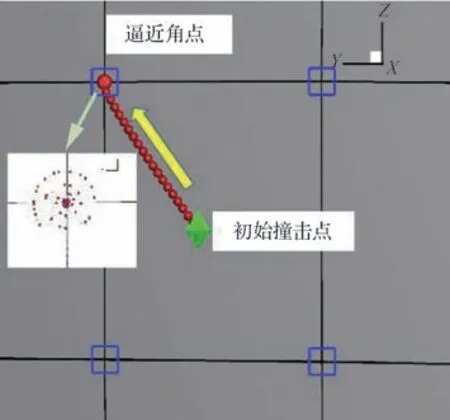
图3 逼近目标点过程示意图Fig. 3 Demonstration of process of closing to target impact point

为了加快收敛，消除目标点附近迭代振荡，采用Nesterov 动量梯度下降方法，通过引入下一步的梯度方向修正当前时间步的前进方向，表达式为

方程（17）中的λk，i和ηk，i分别通过预估校正的方式获得，其中预估值的表达式为

若λk，i和ηk，i的 预 估 值 过 大，可 能 导 致 液 滴 撞击点出现远离目标点的趋势，或是直接飞离物面。因此根据式（20）和式（21），按先后顺序对其进行校正。

在校正过程中，释放位置更新后的液滴若出现上述情况，则减小λk，i和ηk，i，直至更新后的距离函数值小于更新前。

在已知撞击某一网格角点的水滴轨迹后，可以通过类似的技巧逼近得到相邻角点的撞击轨迹，如图4 所示。在逐点逼近过程中，若推进步长小于特定值后，水滴仍飞出壁面或是撞击在非目标点邻近的面网格单元上，将该角点标记为撞击极限点，此时不再查找该点相邻角点的撞击轨迹。该算法的详细计算流程见图5。

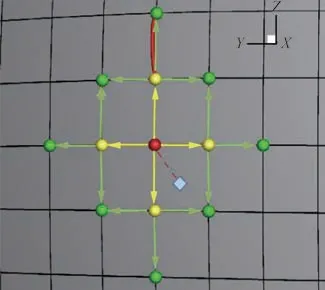
图4 邻点检索算法示意图Fig. 4 Diagram of neighbor search method

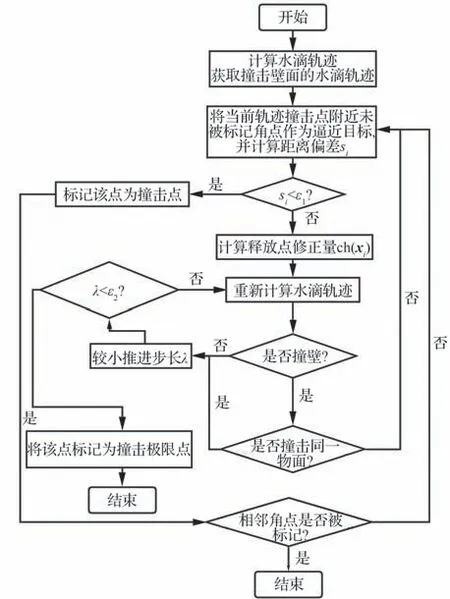
图5 计算流程图Fig. 5 Calculation flow chart

根据物面网格单元各角点所对应水滴轨迹组成的“流管”，通过式（11）计算得到单元中心的水滴收集率。

3 计算结果及分析

分别采用三维圆球、30P30N 平直多段翼、ONERAM6 机翼以及某型短舱构型对上述方法的可行性进行验证。

3.1 三维圆球水滴收集率

计算工况如下：远场来流速度为75 m/s，圆球直径为15.04 cm，远场静压95 840 Pa，，液滴粒径为18.6 μm，采用LangmuirD 多尺度粒径分布模型。迭代逼近过程中的偏移误差设为1.0 ×10-5m，时间积分步长5.0×10-5s，水滴释放平面距模型前缘1.2 m 处，即当水滴轨迹撞击点与目标角点的空间距离小于1.0 ×10-5m 时，认为该轨迹的撞击点与目标角点拟合。

图6 中给出了本文方法计算得到的撞击点分布结果，并与文献［14］所述方法在撞击极限附近加密3 次的撞击水滴阵列进行了比较。图中显示本文计算的撞击点位置与网格角点的重合度良好，且预测的撞击极限与3 次加密后的撞击网格结果基本一致。表明本文方法能够准确预测得到物面水滴撞击域以及撞击极限。

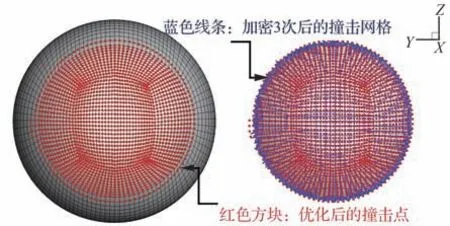
图6 圆球撞击点分布结果Fig. 6 Distribution of impinging point of sphere case

图7为不同计算方法与试验数据［19］的水滴收集率β曲线对比结果。其中，本文计算得到的收集率曲线与试验数据除在驻点处的收集率峰值仍存在一定差异外，两者分布规律基本吻合。通过局部放大图可以观察到，本文改进后的计算结果与FENSAP 计算结果贴合度更好，并且在驻点处的水滴收集率更接近试验数据。图8 比较了依赖插值的拉格朗日流管法和本文方法计算得到的水滴收集率云图。显而易见，本文方法的计算结果较传统方法的插值结果表现出更好的轴对称特征，更加符合实际物理分布规律。上述结果说明本文方法能够克服现有拉格朗日方法中插值对水滴收集率计算结果带来的不利影响，改善了方法的鲁棒性。

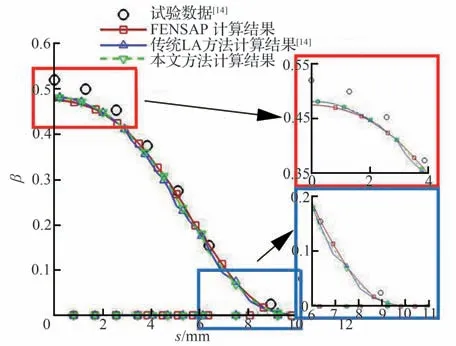
图7 圆球水滴收集率分布曲线比较Fig. 7 Comparison of computational and experimental collection efficiency of sphere case

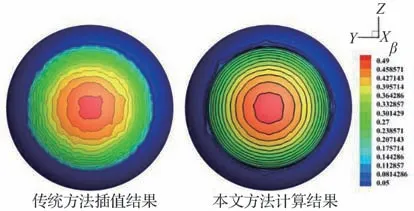
图8 圆球水滴收集率分布云图Fig. 8 Contour of collection efficiency of sphere case

本文方法需要通过迭代运算获得壁面角点的撞击轨迹，而每次迭代都需要重新计算水滴轨迹。因此，相比传统流管方法，本文方法需要耗费更多的计算机时。图9 统计了不同轨迹运算次数的目标点个数分布情况，横轴表示不同的轨迹运算次数区间，纵轴表示与之对应的目标点个数。结果显示大多数目标点的轨迹运算次数小于20。相比在提升计算精度和改善算法鲁棒性上等方面带来的收益，本文方法增加的计算量是可以接受的。另外，可以采用多起点并行计算策略，进一步缩短遍历撞击域内所有角点所需的时间。本节算例采用10 线程并行计算耗费机时33.86 s，与单核计算耗时343.82 s相比有较显著的提升。

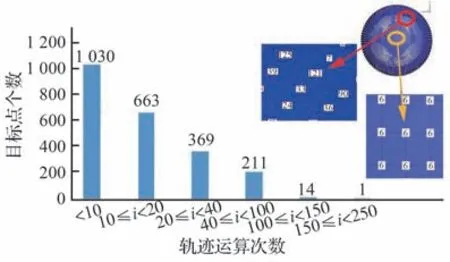
图9 撞击域内水滴轨迹迭代运算次数统计Fig. 9 Statistics of iteration times in impact zone

为了克服因部分角点迭代次数增加导致计算效率下降的困难，下一步工作将对不同的轨迹定位插值方法、邻域模型计算精度以及迭代算法进行研究分析，制定一套能够降低迭代运算量的控制策略。

3.2 30P30N 平直多段翼水滴收集率

计算工况如下：模型弦长111.44 mm，来流速度78 m/s，远场静压95 840 Pa，迎角0°，液滴粒径21 μm，采用LangmuirD 多尺度粒径分布模型。

图10 给出了30P30N 平直多段翼表面多连通域的水滴收集率分布云图。图中显示，水滴撞击域主要位于缝翼前缘和襟翼下翼面，而主翼段没有出现水滴撞击。通过截取模型中截面的水滴收集率分布曲线，与Bidwell［20］报告中公开发布的试验测量结果进行比较，验证计算结果的准确性。如图11 和图12 所示，计算得到的缝翼处的水滴收集率分布规律与试验数据吻合度较高，襟翼上的水滴收集率峰值虽存在一定差异，但整体趋势基本相同。上述结果表明，在复杂气动特性影响下，本文方法能够保证较高的计算精度。

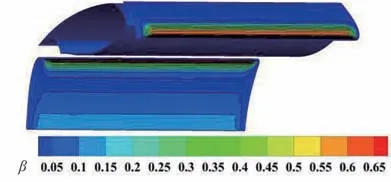
图10 30P30N 平直多段翼水滴收集率计算结果Fig. 10 Results of collection efficiency of 30P30N multi-elements airfoil

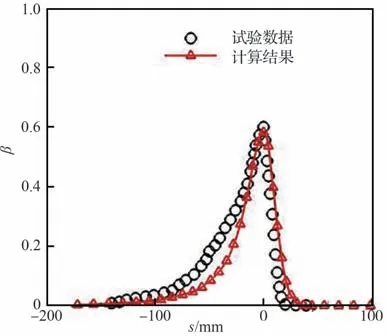
图11 缝翼水滴收集率分布曲线Fig. 11 Comparison of computational and experimental collection efficiency on the slat

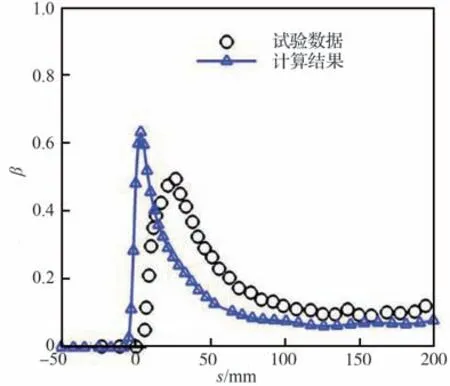
图12 襟翼水滴收集率分布曲线Fig. 12 Comparison of computational and experimental collection efficiency on the flap

3.3 ONERA-M6 机翼水滴收集率

计算工况如下：平均气动弦长为0.54 m，展长为1.0 m，来流 速 度52 m/s，迎角6°，远 场 静 压101 325 Pa，液滴粒径20.0 μm。

图13 给出了ONERA-M6 机翼水滴收集率计算云图。图14 截取了机翼沿展向站位在20%，60%和90%处的收集率分布曲线，并与文献［21-22］的计算结果进行了对比。结果显示本文计算结果与文献数据保持了良好的一致性。

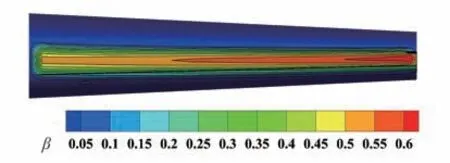
图13 ONERA-M6 机翼水滴收集率计算结果Fig. 13 Results of collection efficiency of ONERA-M6 wing

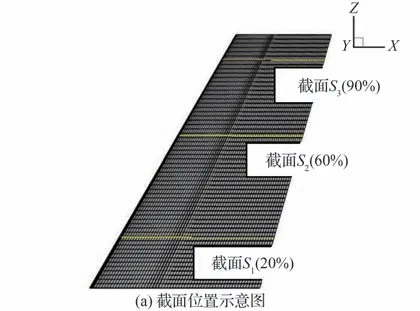
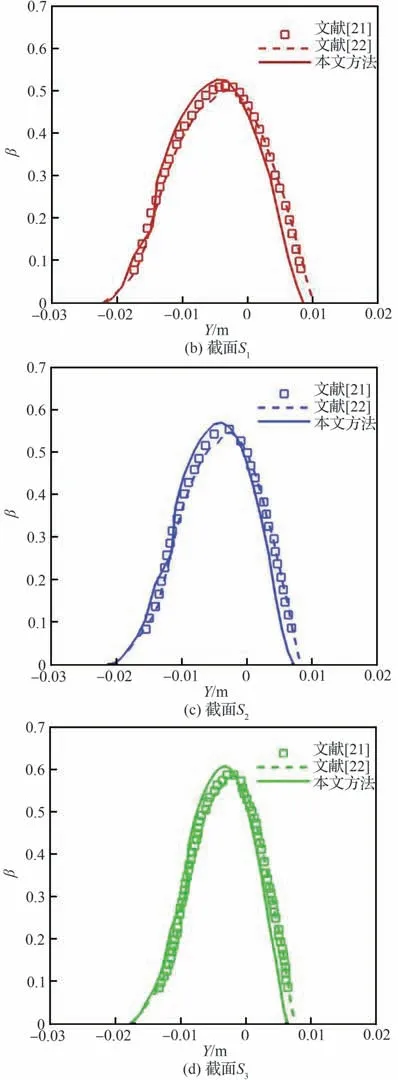
图14 沿展向不同站位处S1-S3水滴收集率曲线Fig. 14 Comparison of collection efficiency on Sections S1-S3

图15给出了不同迎角下的水滴收集率计算结果。可见，随着迎角的增大，除了上下极限位置发生改变外，机翼展向的收集率分布规律也有明显变化，翼梢处的水滴收集率变化受迎角影响更加敏感。

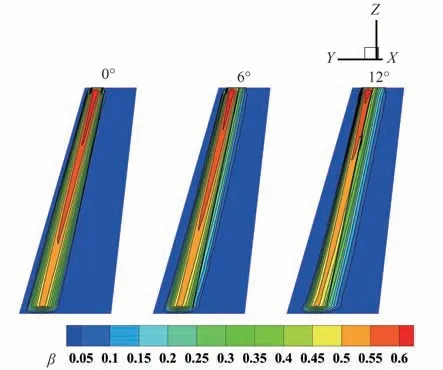
图15 不同迎角下的水滴收集率分布云图Fig. 15 Contour of collection efficiency with different angles of attack

3.4 某型发动机短舱及整流罩水滴收集率

本节算例是一个典型的旋成体模型，采用非结构类型的流场网格，如图16 所示。计算工况如下：来 流 速 度67 m/s，迎 角0°，远 场 静 压101 325 Pa，水滴粒径44.5 μm。

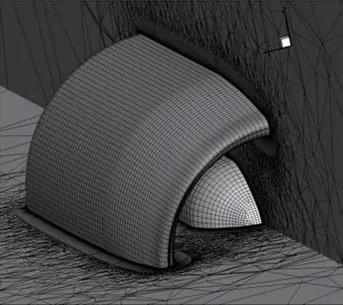
图16 短舱流场网格展示Fig. 16 Flow field grid of engine nacelle model

图17比较了本文方法与FENSAP 计算得到的物面水滴收集率云图。从图中可见：①两者计算结果一致性较好，预测得到的撞击域以及撞击极限位置基本相同，且水滴撞击区域主要位于短舱唇口与帽罩前部段；②本文方法结果表现出了良好的对称分布特征，且等高线过渡光滑，撞击极限刻画清晰。

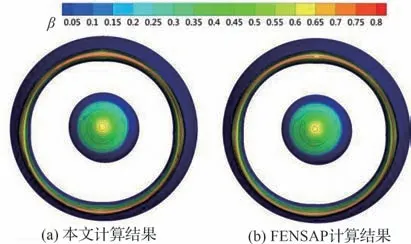
图17 短舱水滴收集率云图Fig. 17 Contour of collection efficiency of engine nacelle model

图18和图19 进一步比较了垂直于Y轴和Z轴中截面上的收集率曲线。结果显示，两者预测的撞击极限位置以及曲线分布趋势基本一致，仅在帽罩和短舱驻点区域的收集率峰值存在一定差异。

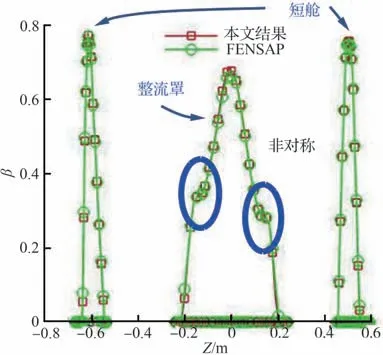
图18 垂直Y 轴中截面水滴收集率曲线对比Fig. 18 Comparison of collection efficiency on the section vertical Y-axis

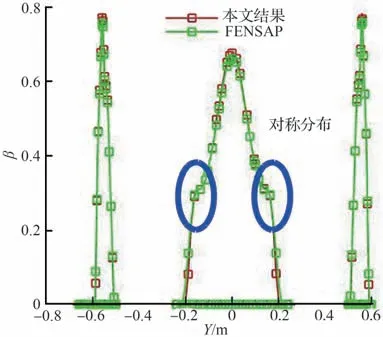
图19 垂直Z 轴中截面水滴收集率曲线对比Fig. 19 Comparison of collection efficiency on the section vertical Z-axis

4 结 论

1） 基于梯度下降法发展了一种水滴收集率计算方法。该方法通过自适应地调控释放点位置，以匹配撞击点和网格节点，避免了插值误差对计算结果带来的不利影响，使物面水滴收集率表征结果更加光滑。

2） 计算结果与文献数据吻合良好，并且该方法在三维平直多段翼、变迎角后掠翼及发动机短舱的水滴收集率计算中表现出良好的鲁棒性，具备模拟三维复杂外形水滴撞击特性的能力。

3） 本文方法需要依赖已知的一条或多条水滴撞击轨迹开展后续计算。为了进一步完善本方法的计算流程，提高程序的通用性能，下一步工作，将利用水滴轨迹的最小壁面距离信息，实现初始撞击轨迹的快速预测。