一般曲线坐标系下概率密度函数方法及其在超声速燃烧中的应用

关清帝，梁剑寒，张林，陈文武，陈玉俏

国防科技大学 空天科学学院 临近空间技术研究所，长沙 410073

超燃冲压发动机燃烧室中燃烧过程十分复杂，湍流、激波、火焰相互耦合，火焰结构一般高度褶皱、破碎，通常还伴随局部熄火、再燃、闪回等复杂过程［1］。在超声速条件下，由于流动速度极快，湍流流动与化学反应的特征时间尺度处于相当的量级，湍流与化学反应紧密耦合在一起，相互作用十分剧烈。超声速、强非定常效应等极端条件带来了一系列值得深入研究的可压、非平衡复杂流动燃烧行为［2］，给超声速湍流燃烧模拟带来了巨大的挑战。又由于化学反应源项的强非线性，对大涡模拟（Large Eddy Simulation， LES）方法而言，很难对滤波后的化学反应源项进行准确建模，湍流燃烧模型是LES 准确模拟超声速湍流燃烧的关键。

目前，超声速流中比较常用的湍流燃烧模型包括火焰面进度变量模型［3］、部分搅拌反应器模型［4］、线性涡模型和一维湍流模型［5-6］以及输运型概率密度函数（Probability Density Function， PDF）模型［7］等。在这些模型中，输运型PDF 方法可以精确处理湍流与化学反应的相互作用，适用于任何复杂的湍流燃烧模式，因此被认为是最可信的湍流燃烧模型之一［8］。输运型PDF 方法从湍流的随机特性出发，基于Navier-Stokes 方程建立并求解湍流物理量的单点联合概率密度输运方程。湍流物理量最基本的可预测性是它的概率及其概率密度分布。已知随机变量的概率密度分布，则可以求解包括化学反应源项在内的任意复杂和任意高阶的单点矩，因此PDF 方法理论上可以精确地处理湍流化学反应相互作用。

PDF 方法体系的建立，主要来源于Pope［7］的开创性工作，其对PDF 方法的理论基础、模化方法以及求解过程都进行了完整的论述。Givi［9］首先将PDF 方法的思想应用于LES 滤波化学反应源 项的 封 闭，Pope［10］随 后 提出了滤 波PDF的概念，Gao 和O'brien［11］依此推导并建立了滤波PDF的输运方程。此后，国内外学者在不可压流中开展了大量的LES-PDF数值模拟。Jaishree［12］采用LES-PDF 方法对Sandia Flame D、E 和F 进行了数值模拟，与实验结果对比，不论是平均量还是脉动量，均与实验结果符合较好。杨越等［13］采用LES-PDF 方法对非预混CO/H2射流火焰进行了模拟，与DNS（Direct Numerical Simulation）结果进行了对比验证，结果显示温度以及主要组分的质量分数与DNS 结果符合很好，LESPDF 方法较好地预测了火焰的局部熄火与再燃过程。总体上，PDF 方法在不可压湍流燃烧中取得了很好的效果。

由于在模拟湍流燃烧相互作用方面的潜在优势，PDF 方法也开始逐步向超声速流发展。Jaberi 等［14］首次将可压缩LES 求解器与PDF 相结合，发展了可压缩LES-PDF 方法，在二维无反应时间混合层算例中初步验证了PDF 方法在可压缩流中的可行性。Banaeizadeh 等［15］进一步发展了这种可压缩LES-PDF 方法，在激波管和无反应超声速同轴射流中开展了相应的数值测试。最近，Komperda 等［16］将可压缩PDF 与间断谱元方法相结合，对球形域中的爆炸过程进行了数值模拟。在作者团队先前的工作［17-18］中，发展了一种守恒可压缩LES-PDF 方法。该方法在激波管和时间反应混合层中得到了初步验证，结果表明守恒可压缩PDF 方法显著提高了能量解的精度。这些工作在可压缩LES-PDF 方法建模等方面取得了重要的进展，但是目前的大多数模型仅在无反应流或者简单反应流中进行了验证。超燃冲压发动机燃烧室中燃烧过程十分复杂，很有必要在实际构型中开展模型验证工作。

随着可压缩PDF 模型的不断完善和数值方法的发展，最近的一些研究也开始将PDF 方法应用于比较实际的可压缩湍流燃烧问题。Validi等［19］对快速压缩机中的湍流射流火焰进行了LES-PDF 模拟，定性比较了温度场计算结果。Ranadive［20］模 拟 了Cheng 等［21］的超声速射流火焰，与实验和层流有限速率模型结果进行了比较详细的定量对比。最近，Abdulrahman 等［22］使用LES-PDF 方法模拟了非预混和预混的分布式燃烧过程，PDF 预测的轴向平均速度与实验符合较好。虽然上述部分工作开始应用于比较实际的超声速燃烧问题，但是采用的网格仍为简单笛卡尔网格，该网格及其数值求解框架难以应用到实际的超燃冲压发动机构型，极大地限制了LESPDF 方法在实际发动机燃烧室中的应用。

总体来说，目前PDF 方法在超声速流中的发展还十分初步，大多数可压缩LES-PDF 方法只在简单笛卡尔网格下进行了方法验证，可压缩LES-PDF 方法在实际构型中的研究和应用还十分缺乏。为了将该方法应用于发动机燃烧室模拟，需要发展适用于复杂构型的LES-PDF 方法。同时复杂构型下LES-PDF 耦合方法，粒子追踪方法以及大规模并行计算等方面，都还有待深入的研究。本文在前期可压缩LES-PDF 工作的基础上，基于多块结构网格，实现了基于曲线坐标的粒子追踪方法，建立了曲线坐标LES-PDF 方法，使可压缩LES-PDF 方法适用于复杂构型计算。

1 基本控制方程

1.1 可压缩LES 控制方程

LES 方法通过对湍流运动的滤波，将湍流脉动分解为可解的大尺度运动和需要封闭的小尺度脉动。可解尺度湍流运动直接求解，小尺度湍流脉动的质量、动量和能量输运对大尺度运动的作用采用亚格子模型进行封闭。对Navier-Stokes 方程进行Favre 滤波，得到大涡模拟控制方程为

式中：t为物理时间；x为物理坐标；i为空间维度；ui为i方向的速度分量；ρ为密度；p为流场压力；δij为Kronecker 函数；τij为黏性应力张量；E为总能；qi为i方向热通量；Yα、Vi，α和ω̇α分别为组分α的质量分数、i方向扩散速度以及质量生成率；“-”表示空间滤波；“～”表示Favre 滤波；上标“sgs”表示未封闭的亚格子项。其中τsgsij为亚格子黏性应力，采用一方程Yoshizawa 模型［23］进行封闭：

其中：ksgs为亚格子湍动能；νt为涡黏系数，由涡黏输运方程直接求解；Sij为应变率张量。

Hsgsi为亚格子焓通量，Ysgsi，α为亚格子组分对流通量，这2 项均采用梯度扩散假设进行封闭：

式中：H为总焓；Prt和Sct分别为湍流普朗特数和湍流施密特数，在本文的模拟中，均为0.72。

1.2 曲线坐标PDF 输运方程

本文仅考虑标量PDF，在标量PDF 方法中，直接求解热力学标量ϕ的联合概率密度函数输运方程，其中ϕ包括Ns个组分的质量分数以及显焓h。可压缩流中标量PDF 定义为

式中：ϕ和ψ分别表示标量向量和标量向量的样本空间为笛卡尔物理空间坐标；y为x对应的积分变量；δ（·）为细粒密度函数；G（·）为滤波核函数。由标量守恒方程，可以直接推导建立笛卡尔坐标下的PDF 输运方程：

式中：为可解速度；Γ为扩散系数，为分子扩散系数和湍流扩散系数之和；ϕα为组分α的质量分数；Sα为组分α的化学反应源项；Ωm为标量混合频率；ψα为ϕα对应的样本空间。式（9）等号左边的2 项为PDF 瞬时项和对流项。式（9）等号右侧第1 项代表湍流脉动和分子扩散导致PDF 在物理空间的输运；第2 项为分子扩散项引起的PDF在组分空间的输运，采用最常用的IEM（Interaction by Exchange with the Mean）小尺度混合模型进行封闭；第3 项表示化学反应以及可压缩项引起的PDF 在组分空间的输运。

式（9）给出的输运方程中化学反应源项Sα可以展开为

式中：ω̇α为 组分α的质量生成率；α=Ns+1 时，Sα表示显焓方程的源项，为反应释热ω̇T和可压缩高速源项Sh之和；Sh的表达式为

由于坐标变换只涉及到物理空间，所以本文重点关注跟物理空间坐标相关联的项，忽略对可压缩项和反应源项等单点源项过程的处理。对于超声速流中反应源项和可压缩项的建模可见作者团队前期超声速PDF 方法的建模工作［18］。

对式（9）两端同时除以J，J的表达式为

式中：J为坐标变换系数矩阵对应的行列式值；ξx、ξy、ξz、ηx、ηy、ηz、ζx、ζy、ζz为度量系数。利用一般曲线 坐 标 系(ξ，η，ζ，τ)和笛卡尔直角坐标系(x，y，z，t)之间的转换关系，进行坐标变换。

为简洁起见，这里直接给出推导整理后的一般曲线坐标系下的PDF 输运方程：

式中：ξ=[ξ，η，ζ]为一般曲线坐标系下的空间坐标；Fξϕ=Fxϕ/J表示一般曲线坐标系下的标量概率密度函数。为逆变速度，其表达式为

其中：u、v、w为物理空间的速度分量。

对流项系数Ai为

可以看出，坐标变换只涉及物理空间，与标量空间无关。由此得到了完全封闭的曲线坐标下PDF 输运方程，可以进行数值求解。

2 数值求解方法

2.1 曲线坐标系下LES 离散方法

采用有限差分方法对曲线坐标下LES 控制方程进行数值离散，曲线坐标下控制方程的具体形式为

式中：Q为守恒变量矢量，表达式为

Ec、Fc、Gc为对流通量矢量；Ev、Fv、Gv为黏性通量矢量。式（17）中各项形式较为复杂，这里不再详细展开，具体表达可以参见流体力学教材。

本文采用的可压缩LES 求解器在超声速湍流流动、燃烧模拟中已经进行了大量的数值验证［24-25］。时间方向的离散采用具有TVD（Total Variation Distance）性 质 的 三 阶Runge-Kutta 方法。空间上对流项和黏性项的离散分开进行，对流项具有很强的非线性，采用五阶WENO［26］格式离散，黏性项体现为物理过程中的耗散，没有明显的方向性，采用简单的二阶中心差分格式进行离散。

2.2 曲线坐标系下Monte Carlo 粒子方法

PDF 输运方程的维数很高，用传统的有限差分等方法求解计算量过大，一般采用Monte Carlo 粒子方法求解。在粒子方法中，流体由大量的拉格朗日粒子来描述，每个粒子根据随机微分方程随时间演化。为了得到对应的曲线坐标下的随机微分方程，引入Fokker-Planck 的矢量形式。对多维扩散过程，其转移密度存在，且满足Fokker-Planck 方程：

式中：f为转移密度函数；d'为转移密度函数的维度；ys为状态空间。式（19）右端第1 项Bij为扩散项，第2 项a为漂移项。其对应的扩散过程为

其中：Ui为随机变量；U为随机变量的样本空间；ai[U(t)，t]称为漂移速度，而bij[U(t)，t]称为扩散速度，两者均为随机变量的函数；W表示维纳随机过程。

此外，民立中学历来也有演剧祝圣的活动，直到1908年8月，其演剧祝旦活动受到王安民的指责，从此不再举办演剧。《新剧史》详细记载了这一事件：

结合式（13）所示的曲线坐标下PDF 输运方程，可以得到对应的粒子随机微分方程。这里直接给出曲线坐标下ξ方向粒子的随机微分方程为

式中：上标“*”表示粒子所在位置的物理参数；U为ξ方向粒子的逆变速度分量；dτ为曲线坐标下的时间增量；dWi代表维纳随机过程［27］的增量。粒子在逆变速度、分子输运以及亚格子湍流扩散作用下在计算空间移动，而粒子标量在小尺度混合、化学反应以及可压缩高速源项的作用下发生变化。粒子随机微分方程所对应的Fokker-Planck 方程与模化后的标量PDF 输运方程形式一致，通过概率相似体系建立起了Monte Carlo粒子和真实流体运动的关联。

粒子位置以及标量的演化通过王海峰等［28］发展的弱二阶算子分裂格式进行。粒子随机微分方程可以分裂为3 个具体过程，分别是计算空间的输运（T），标量空间的混合（C）以及标量空间的单点化学反应（R）。该二阶精度的算子分裂格式称为“TCRCT”，依次包含以下5个过程：物理空间输运半时间步，标量空间半时间步的亚格子混合，整个时间步长的化学反应，另外半个时间步的亚格子混合以及位置空间的输运。上述分裂格式的优势是可以保证化学反应步不分裂，因为在所有过程中，化学反应计算占用时间最长，尤其在采用详细化学反应机理时，化学反应计算开销更大。

2.3 曲线坐标系下LES-PDF 耦合方法

LES 有限差分求解器和PDF 粒子求解器需要耦合求解，耦合过程如图1 所示。LES 有限差分求解器求解大涡模拟流动和组分方程，计算得到LES“可解场”的分布。PDF 粒子求解器计算粒子随机微分方程，并通过系综平均得到PDF“粒子场”平均量。LES 向PDF 提供滤波速度、扩散系数、可压缩源项等物理量用以PDF 粒子输运，PDF 则向LES 反馈化学反应源项以完全封闭大涡模拟组分方程。

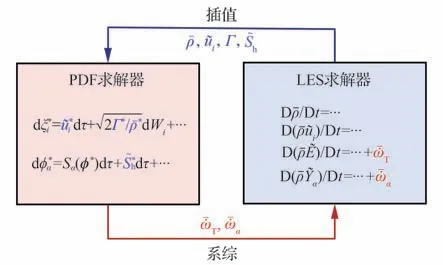
图1 LES-PDF 方法耦合示意图Fig. 1 Schematic diagram of LES-PDF coupling

上述耦合过程通过混合拉格朗日粒子/欧拉网格方法实现，该方法如图2 所示，每个网格中分布若干PDF 粒子。LES 向PDF 粒子传递的滤波速度等物理量，由网格节点向粒子位置处进行插值，得到该粒子处的具体值。在本文中，为简便起见，采用了线性插值方法。从PDF 粒子传给LES 求解器的值，则由选定区域中粒子的系综平均得到：

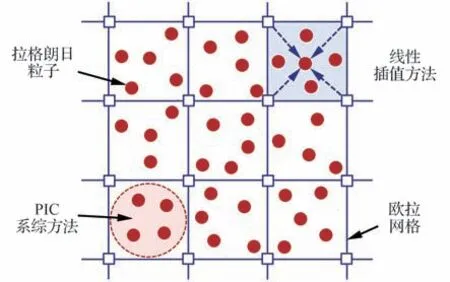
图2 混合拉格朗日粒子/欧拉网格方法示意图Fig. 2 Schematic diagram of hybrid Lagrangian particle/Eulerian mesh method

式中：Np为网格中粒子总数；ω()n为第n个粒子的权重；ϕ(n)为第n个粒子的标量值；Q为粒子标量的单点统计。为了与插值过程相匹配，本文选定的系综区域为单个网格，即采用PIC（Particles In Cell）系综方法。粒子在计算空间输运过程中，由于PDF方法的随机效应，可能出现部分网格内粒子数过少而部分网格粒子数过多的情况，这会明显增加粒子系综统计误差，且导致计算负载的不平衡。本文通过设置平均粒子数目对网格中粒子的数量进行限制，保证粒子数密度在倍网格平均粒子数之间。本文的流动混合算例中，网格平均粒子数目设置为50，燃烧算例中，由于粒子组分较多且化学反应计算量较大，网格平均粒子数设置为30。需要说明的是，在曲线坐标框架下，基于计算坐标，便于构造高阶的插值和系综方法。在超声速流中，流场速度等物理量变化大，高阶的速度插值和系综统计方法可能有助于提高计算精度。

综上，LES-PDF 方法的基本算法流程可以概括如下：首先对LES 流场进行初始化，PDF 粒子的初始质量、能量（显焓）以及组分等参数由LES 流场初始化参数计算得到。然后开始计算LES 质量、动量和能量方程，求出LES 密度、速度、温度和压力，在此基础上计算得到高速源项和湍流扩散系数等需要传递给PDF 的流场信息。下一步将滤波速度、高速源项以及湍流扩散系数等插值到PDF粒子所在位置处。之后，PDF 粒子根据式（21）和式（22），进行位置空间的粒子追踪和标量空间的混合和化学反应，粒子的位置和标量参数发生变化。最后，根据网格内所有粒子的系综平均求出PDF粒子场统计结果，并将粒子场计算的化学反应源项传递给LES 求解器，求解得出新的LES 可解场信息，如此完成一个时间步长的耦合求解过程。本文提出的曲线坐标LES-PDF 方法，主要对粒子位置空间的追踪过程进行了改进，提出了基于一般曲线坐标系的粒子追踪方法。

2.4 曲线坐标系下粒子追踪方法

本文提出的一般曲线坐标下LES-PDF 方法中，采用多块结构网格。多块网格由局部结构网格组成，局部块结构网格相互拼接形成一个全局网格。曲线坐标下的粒子追踪方法也是基于多块结构网格进行实现。

传统方法基于粒子物理速度(u，v，w)在位置空间进行移动，如图3（a）所示。物理坐标下粒子追踪过程需要判断粒子和网格之间的相对位置关系，即粒子与网格的4 条边进行矢量计算才能判断是否位于当前网格中。同时从A到B的移动过程中，还要进行搜索以确定粒子的移动路径。PDF 方法中，网格中包含大量粒子，每一时间步均需要进行搜索和定位，在物理坐标系下进行追踪相对繁琐和耗时。

曲线坐标下的追踪方法，即通过坐标变换，将传统在物理坐标下的粒子追踪过程，转换到曲线坐标系下进行。如图3（b）所示，粒子在计算空间根据逆变速度(U，V，W)移动。曲线坐标下粒子追踪的一个主要特点是，在单块网格中，粒子的计算坐标(ξP，ηP，ζP)与网格单元索引(Ic，Jc，Kc)直接相关：

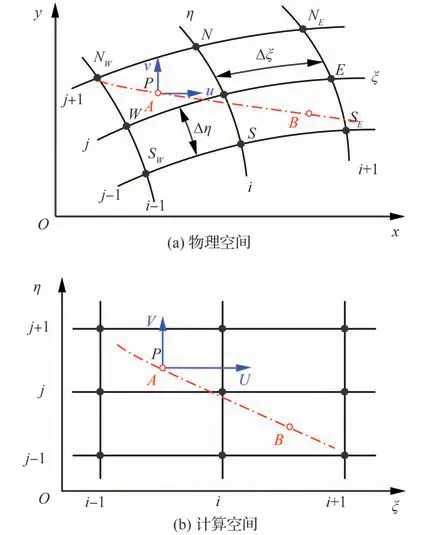
图3 单块网格内曲线坐标粒子追踪方法Fig. 3 Curvilinear particle tracking method within a single block grid

式中：floor 表示向下取整。粒子所在位置的曲线坐标向下取整即为粒子所在网格的网格索引，从A向B的移动中，粒子不需要进行额外的搜索和定位。

如何实现粒子在多个网格分区间的连续追踪，是多块结构网格下曲线坐标粒子追踪方法需要处理的一个关键问题。本文提出了一种处理多块网格分区间粒子曲线坐标转换的方法，实现了粒子在多块分区间曲线坐标的连续追踪，其基本过程如图4 所示。

图4 曲线坐标粒子追踪方法流程图Fig. 4 Flow chart of curvilinear particle tracking method

首先计算粒子到网格分区边界的最小时间Δtmin，判断粒子是否移动出当前网格分区。若Δtmin≥Δt，则粒子仍在当前分区中，在当前网格分区中的粒子不需要追踪，直接更新粒子的曲线坐标，若当前的迭代步数n小于给定的最大迭代计算步nmax，进入下一个迭代，否则结束计算。若Δtmin＜Δt则表明粒子将要移出当前分区。对跨越网格分区的粒子需要进行额外的处理。

图5给出了跨越多块网格分区粒子的追踪过程。对要移动出当前网格分区的粒子，首先确定粒子穿越网格的位置C，将粒子先输运至分区边界处，并在边界处更新输运时间Δt=Δt-Δtmin。然后在边界C处，根据边界两侧分区的拓扑关系，进行曲线坐标间的坐标转换，将当前分区1 下的曲线坐标转换为目标分区2 中的曲线坐标。除了位置坐标需要转换外，粒子的逆变速度也要进行相应的转换。位置矢量和逆变速度矢量的坐标转换在数值上需要乘以坐标转换矩阵完成，其中的坐标转换矩阵即表征了2 个分区间的拓扑关系。最后将该粒子进行非阻塞的点对点通信，从当前分区1 发送给目标分区2，并在网格分区2 中从C处开始继续对该粒子进行追踪，重复前面的过程，直到剩余的时间步长Δt变为0。

图5 多块网格间曲线坐标粒子追踪方法Fig. 5 Curvilinear particle tracking method between multiblock meshes

基于上述粒子追踪方法，可以实现全局范围内粒子的连续追踪。实际计算中，只有少部分边界附近的粒子会穿越网格分区，本文提出的曲线坐标粒子追踪方法，单块网格中不需要额外追踪，减少了单块网格内粒子追踪的计算量，同时也很好地处理了多个网格分区结合位置处的粒子追踪过程，十分适合拉格朗日粒子方法的大规模并行计算。此外，为了保证计算空间中粒子追踪的精度，当时间步长过大，粒子穿越多个网格，即时，将时间步长减半，保留剩余的输运时间，重新计算粒子位置，直到粒子剩余的时间步长为0。

3 算例验证

为了验证曲线坐标下LES-PDF 方法的准确性，针对曲线坐标下的关键问题，曲线坐标形式的PDF 输运方程及其粒子随机微分方程，多块分区间的粒子坐标转换，通信和连续追踪，以及曲线坐标程序复杂构型的处理能力等问题，从简单到复杂进行逐步的数值验证。

3.1 拉伸网格下Sod 激波管

首先针对一维Sod 激波管问题进行验证。无量纲计算域取为［0，1］，x方向共布置了101 个节点，第1 个和最后1 个网格节点为壁面边界条件。采用的网格为拉伸网格，在激波管中间位置进行了指数加密，激波管中间位置网格无量纲宽度约为0.005，激波管第1 个和最后1 个网格的无量纲宽度为0.025。计算采用的CFL（Courant-Friedrichs-Lewy）数为0.5，无量纲初始条件设为

在该算例中只考虑无黏流，标量PDF 只求解了显焓，主要通过温度和密度等热力学结果来验证方法的准确性。初始的显焓流场由式（25）给定的初始压力、速度以及密度计算得到。在简单拉伸网格下重点验证曲线坐标下可压缩模型以及显焓方程求解的正确性，排除了其他模型和方程的干扰。图6 分别给出了曲线坐标LES-PDF方法计算的无量纲温度和密度结果，从图中可以看出，PDF 计算结果与精确解符合得很好，初步验证了曲线坐标下PDF 输运方程和粒子随机微分方程的准确性。

图6 无量纲温度和密度计算结果Fig. 6 Calculation results of dimensionless temperature and density

3.2 非正交网格下时间混合层

随时间发展的平面混合层流动示意图如图7所示，由2 股相反的平行流发展而成。平均流速度的初值为双曲正切分布uˉ=tanhy，扰动流函数φ取为

图7 时间混合层示意图Fig. 7 Schematic diagram of temporal mixing layer

对应的最不稳定扰动波数β=0.444 6，扰动波长λ=2πβ=14.132 2。由此得到初始速度场为

式中：扰动量级ε取为0.1；无量纲初始压力为p=1/(γMa2c)，Mac为对流马赫数，本文中为0.4，γ=1.4为比热比。初始温度T由Busemann-Crocco 关系确定，T=1+(γ-1)Mac2(1-uˉ2)/2。该算例中除显焓外，PDF 变量中还包含一个被动标量ϕ，主要研究该被动标量的输运和混合，对曲线坐标LES-PDF 方法进行定性和定量的验证。初始时刻上层标量ϕ1=1，下层标量为ϕ2=0，标量剖面由双曲正切函数给定：

式中：δω为初始涡量厚度。选取初始涡量厚度δω为特征长度，基于此计算的雷诺数约为 2 800。

本文考虑的为双周期混合问题，所以x方向计算域包含2 个最不稳定波长，y方向计算域长度与x方向相同，即Lx=Ly=2λ。x方向为周期边界条件，y方向为出口边界。模拟中网格不分区，排除多块网格分区间粒子追踪的干扰，只验证曲线坐标方程以及单块网格内粒子追踪方法的准确性。

分别采用传统LES 方法、曲线坐标LESPDF方法和DNS（Direct Numerical Simulation）进行模拟，其中DNS 网格为1 000×1 000 的正交网格，而LES 和曲线坐标LES-PDF 方法均采用100×100 的非正交曲线网格，网格分布如图8 所示，图中只给出了30 个网格，具体的网格坐标为

图8 非正交曲线网格Fig. 8 Non-orthogonal curvilinear grid

式中：ξ和η为计算坐标；ε为网格扰动量级，取为0.5。

图9给出了t=40时刻被动标量ϕ的分布云图。从图中可以看出，曲线坐标下LES-PDF方法很好地捕捉了上下2股流体的标量界面，粒子分布与DNS计算的标量结果十分接近，表明了曲线坐标LESPDF方法以及单块网格内粒子追踪方法的准确性。

图9 标量ϕ 的分布云图Fig. 9 Contours of scalar ϕ

从图10 中标量一阶矩ϕˉ的计算结果可以看出，曲线坐标PDF 方法与DNS 结果符合得很好，准确预测了大部分的标量细节分布，而LES 的结果则较为光滑。标量二阶矩主要反映了可解尺度的相互作用，可以看出，曲线坐标PDF方法计算的结果不论是特征还是幅值上，与DNS符合得很好。标量二阶矩表征了标量的亚格子脉动效应，该部分传统的LES 由于缺乏亚格子信息，无法模拟，PDF 方法中粒子的随机脉动模拟了亚格子脉动效果，从结果来看，曲线坐标PDF 方法定性地捕捉了混合层亚格子脉动规律，但是在混合层中心位置，预估的亚格子脉动要高于DNS，这可能是由于混合层中心网格加密不足，导致其高估了亚格子脉动效应。

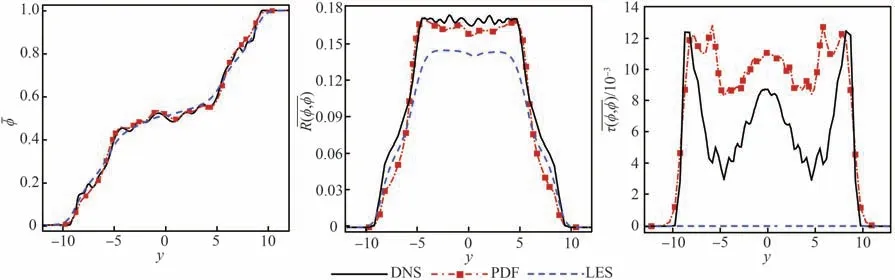
图10 标量统计结果Fig. 10 Scalar statistics results

总体来看，曲线坐标LES-PDF 方法较好地捕捉到了亚格子脉动效应，验证了单块网格内曲线坐标下粒子定位、追踪以及LES-PDF 耦合等方法的准确性。

3.3 多块分区下的圆柱绕流

二维圆柱绕流主要用以验证网格分区间粒子追踪方法的准确性。该算例中PDF 主要求解了显焓方程，通过粒子的温度分布来验证粒子是否正确穿越了分区以及是否正确处理了与激波的相互作用。入口来流马赫数选择为2.5，来流压力为101 325.0 Pa，来流温度为288.15 K。在该条件下，激波正好能穿越多个拓扑分区，能更好地验证曲线坐标下粒子是否被正确输运。入口给定超声速入口条件，上下以及出口边界均采用超声速出口条件，圆柱表面为壁面边界条件。

计算网格拓扑如图11（a）所示，多个分区结合的角点，给粒子追踪方法带来了更大的挑战。从图11（a）中全场粒子分布结果可以看出，在角点位置后，存在一条明显的空粒子带。图11（b）给出了局部放大的粒子、流线以及网格分布。从流场流线可以看出，粒子主要由分区1 向分区5进行移动，存在上下2 条路径。粒子可以正确穿越从分区1、分区4 到分区5 的路径。而粒子由分区1，经过分区2 和分区3，无法正确通过最后的分区边界。数值测试发现，主要是因为分区2 和分区3 在角点存在较大的网格畸变，在进行曲线坐标转换时，粒子逆变速度出现明显偏差，改变了粒子的正确运动方向。为解决上述问题，对角点附近的粒子追踪过程进行修正：① 当前分区和目标分区边界处使用相同的度量系数以及雅可比行列式，对分区边界的度量系数进行光滑；② 粒子进入新的分区后，在新分区重新计算粒子逆变速度。修正后的粒子分布如图11（c）所示，结果显示粒子正确穿越了分区边界，成功解决了空粒子带问题。

图11 网格畸变导致的粒子无法正确穿越边界的问题Fig. 11 Problem of particles not crossing boundary correctly due to mesh distortion

图12进一步给出了传统LES 方法和曲线坐标PDF 方法计算的温度云图对比。可以看出，LES 网格显示结果和PDF 粒子计算结果基本相同，激波位置以及尾迹的分布具有很好的一致性，定性验证了多块分区网格下曲线坐标粒子追踪方法和粒子边界条件的准确性。

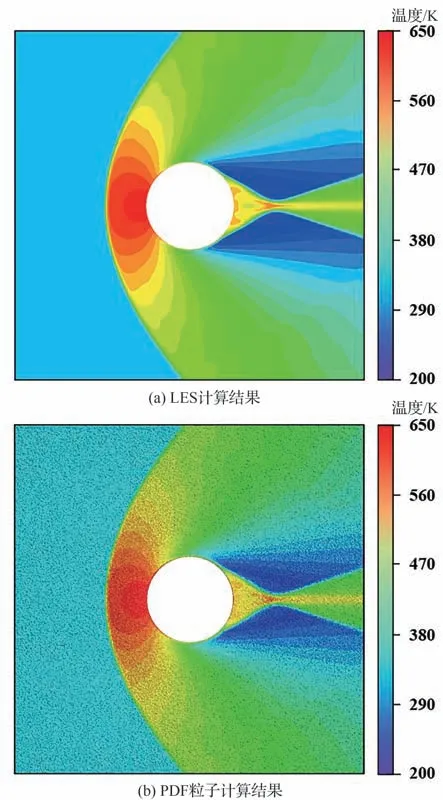
图12 LES 和PDF 温度结果对比Fig. 12 Comparison of LES and PDF temperature results

3.4 复杂拓扑下的球头绕流

进一步在三维球头绕流算例中验证曲线坐标LES-PDF 方法在三维复杂拓扑中的计算稳定性。图13（a）给出了三维球头绕流算例的网格拓扑，此次计算中总共分了48 个分区，网格拓扑相较于二维圆柱绕流进一步复杂化。同时，分区的顶点也是典型的多块接合点问题，而且这4 个顶点位置，网格的畸变均比较大。球头绕流的计算条件和设置与二维圆柱绕流基本一致，PDF 主要求解了显焓能量方程，通过能量场（温度）的分布定性地显示曲线坐标LES-PDF 方法的计算结果。图13（b）给出了PDF 粒子的分布云图，其中粒子由温度着色，图13（c）给出了中心截面上PDF 温度分布。上述结果表明当前曲线坐标下的LES-PDF 方法具备处理三维复杂拓扑下的粒子追踪和相应计算的能力。

图13 球头绕流网格拓扑及PDF 温度计算结果Fig. 13 Mesh topology of spherical blunt and temperature results of PDF method

4 超声速同轴射流火焰数值模拟

4.1 计算构型和边界条件

基于Evans等［29］的超声速同轴射流实验，在实际超声速湍流燃烧问题中对曲线坐标LES-PDF方法及其数值求解框架进行全面的验证。Evans超声速同轴射流实验基本构型如图14 所示，内外喷管形成2 股平行的超声速射流，内部为低温氢气燃料，外部为高温的污染空气氧化剂流。内部喷管外径d为 9.525 mm，唇口厚度为 1.5 mm。为简化计算构型，本文未考虑喷管内部的流场结构。计算域轴向长度（Lx）为30 倍内射流直径，径向长度（Lr）为2 倍射流直径，本文中计算域用内射流直径进行无量纲化。轴向均匀分布480 个网格，周向的网格数目均为120 个，径向网格在喷管内外壁面均进行加密，入口截面上的网格分布如图15 所示，网格拓扑为典型的“O-Block”分布。

图14 同轴射流火焰示意图Fig. 14 Schematic diagram of coaxial jet flame

图15 入口截面网格和无量纲流向脉动速度分布Fig. 15 Mesh and dimensionless streamwise pulsation velocity distribution in entrance section

内外射流入口均采用超声速入口条件，根据Evans 等［29］的实验参数直接给定。内外射流详细的流动参数如表1 所示。

表1 同轴射流火焰实验参数Table 1 Parameters of coaxial jet flame experiment

本文的计算域以及边界条件设置与刘朝阳等［30］的工作基本一致。刘朝阳等［30］采用的网格总数约为3 500 万，燃烧模型为设定型PDF 模型。本文的网格总数约560 万，采用数字滤波方法给定了如图15 所示的湍流边界层，边界处厚度约为 2.5 mm。化学反应计算采用Conaire 等［31］的9 组 分（H2、O2、H2O、H、O、OH、HO2、H2O2、N2） 21 步氢/空气反应机理。基于选择的反应机理，PDF 求解显焓的能量方程以及9 个组分的输运方程，在燃烧条件下全面验证曲线坐标LESPDF 方法的准确性。

4.2 燃烧流场结构

氢气射流与高温燃气射流相互作用，在下游发展形成图16 所示的超声速抬举射流火焰，图中为射流中心截面上流场瞬态分布。从图16（a）的轴向速度分布可以看出，由于唇口的存在，内外2股射流在入口处形成2 道膨胀波，在射流中心处相交汇聚。膨胀波反射形成2 道激波，并在正中心出现一个马赫盘。内外射流之间具有很强的速度剪切，Kelvin-Helmholtz（K-H）不稳定性导致剪切层失稳。图16（b）给出了混合分数结果，射流标量界面在K-H 涡结构作用下逐渐变得褶皱，向下游的发展过程中逐渐掺混。在该实验中，高温燃气的静温为1 495 K，远超氢/空气的自着火温度。如图16（c）所示，射流经过一小段混合距离之后，H2O 开始大量出现，并且H2O 的分布主要集中在K-H 涡结构中，表明燃烧主要发生在这些混合充分的K-H 涡结构中。图16（d）进一步给出了燃烧释热率分布云图，可以明显看出在射流入口附近存在一个明显的释热率峰值区域，其表征了火焰基底位置。总体上，曲线坐标LES-PDF 比较准确地反应了射流火焰流场的基本结构。

图16 轴向截面流场云图Fig. 16 Contours of flow field in axial plane

4.3 统计结果对比

图17进一步给出了曲线坐标LES-PDF 方法计算的4个轴向位置上H2、O2、H2O 和N2沿 径向的平均组分分布，并与实验结果和刘朝阳等［30］的设定型PDF 数值模拟结果进行对比。

图17（a）和图17（b）给出了近场x/d=8.26和x/d=15.5 截面上的组分分布。近场的2 个轴向位置处的组分分布规律基本一致。由于剪切层中涡扩散和分子扩散作用，H2燃料向高温氧化剂流中扩散，同时K-H 涡结构中混合较好的位置，开始出现着火，进一步消耗燃料，H2质量分数沿径向逐渐下降。外部高温燃气中的O2和N2则与之相反。近场燃烧仅在薄剪切层中进行，产物H2O 的峰值位于剪切层内。整体上曲线坐标LES-PDF 方法计算的结果与设定型PDF 模型的结果相似，均低估了近场剪切层中的燃烧强度。

图17 不同轴向位置处径向组分分布Fig. 17 Radial component distribution at different axial positions

图17（c）和图17（d）给出了下游x/d=21.7和x/d=27.9 火焰区内的平均组分分布。在下游位置，从产物H2O 的分布可以看出，火焰区域明显扩大。而射流中心的H2浓度比实验值偏高，说明燃料消耗不足，预测的燃烧强度仍低于实际情况。曲线坐标LES-PDF 方法计算的产物H2O的分布范围与实验更加接近，而设定型PDF 模型的计算结果则相对低估了下游火焰区内的H2O的生成和H2的消耗。此外，本文计算的N2结果存在一定的不足，明显高估了N2向射流中心的扩散。总体来看，本文的网格数量相比刘朝阳等［30］小接近一个量级，尽管预测的被动标量N2的分布稍 差，但H2和O2等 反应标量 与刘朝阳 等［30］的 设定型PDF 模型计算的结果基本相当，尤其是下游火焰区内反应生成物H2O 的分布明显优于设定型PDF 模型，这些定量结果表明了曲线坐标LES-PDF 方法的准确性。

5 结 论

1）针对超燃冲压发动机燃烧室中超声速湍流燃烧数值模拟的实际需求，面向发动机实际构型，建立了一般曲线坐标系下的LES-PDF 方法。基于多块结构网格，对PDF 输运方程和粒子随机微分方程进行了坐标变换，实现了基于曲线坐标的粒子追踪和粒子边界条件，解决了多块网格分区间粒子连续追踪问题，实现了复杂构型下的曲线坐标LES-PDF 计算。

2）由简单到复杂逐步对曲线坐标LESPDF 方法中的关键问题进行了充分的验证。一维Sod 激波管和二维时间混合层算例中，曲线坐标LES-PDF 方法计算的结果与精确解和直接数值模拟结果符合得很好，表明了曲线坐标形式的PDF 输运方程及其粒子随机微分方程的正确性。二维圆柱绕流算例中发现，在多个分区接合的角点位置，由于网格畸变较大，导致粒子速度计算出现较大误差，导致其无法正确穿越分区边界，在网格分区角点后出现了一条明显的空粒子带。通过对分区间度量系数和雅可比行列式的光滑，并在新分区重新计算粒子速度，成功解决了多块分区间粒子丢失问题。三维复杂拓扑球头绕流结果进一步证明了当前曲线坐标LES-PDF 方法对复杂拓扑的处理能力。

3）超声速同轴射流火焰模拟中，曲线坐标LES-PDF 方法给出了较为准确的射流火焰流场基本结构，同时不论是近场还是远场，该方法预测的组分分布整体上与实验均吻合较好，尤其在远场火焰区内，其给出了更准确的反应生成物H2O 的分布，在实际超声速燃烧问题中定量验证了曲线坐标LES-PDF 方法的准确性。