一种基于幅值和波数的耗散控制方法
魏皇生,黄柱,席光
西安交通大学 能源与动力工程学院,西安 710049
大涡模拟(Large Eddy Simulation, LES)可以用于研究如湍流的复杂流动问题,近年来受到越来越多的关注[1-2]。由于只解析大尺度结构,LES 的最高分辨率集中在对湍流演化有重要影响的湍流惯性子区域。然而,可压缩流中不仅存在如湍流的复杂流动结构,还存在大量间断。为了模拟间断,数值格式往往具有较大的耗散和很强的非线性。但是,过大的耗散会抹平流动细节,且强非线性会诱发如“数值湍流”的小尺度非物理波动[3]。高质量的LES 既要分辨大尺度流动结构,又要抑制小尺度非物理波动,这对耗散控制方法提出了挑战。
在面向超声速流动的高精度方法中,加权本质无振荡格式(Weighted Essentially Non-Oscillatory Schemes, WENO)[4-5]可以根据局部流场的光滑程度动态地调整耗散,是具有代表性的激波捕捉格式[6]。在此基础上,为了更好地分辨大尺度流动结构和抑制小尺度非物理波动,人们对耗散的控制方法进行了大量研究。
为了更好地分辨大尺度流动结构,基于保单调技术,Balsara 和Shu[7]构造了具有更小色散误差与更高精度的WENO 格 式。Henrick[8]和Borges[9]等通过改进光滑指示器,改善了WENO格式在奇点处精度下降的问题。为了降低耗散,Martín 等[10]通过引入顺风模板构造了具有中心型背景模板的WENO-SYMOO 格式。在此基础上,Hu 等[11]通过修改光滑因子,构造了自适应中心/迎风格式的WENO-CU 格式,显著降低了耗散。最近,Fu 等[12-13]基于新的模板选择和加权策略,提出了定向本质无振荡格式(Targeted Essentially Non-Oscillatory schemes, TENO),进一步降低了格式的耗散。Hill 和Pullin[14]通过在光滑区域使用针对LES 进行优化的中心差分格式(TCD),在间断附近使用WENO 格式,构造了具有更高分辨率的混合格式。
针对小尺度非物理波动,Pirozzoli[15]指出,数值格式中有必要包含一定的耗散以抑制高波数的数值振荡。为了对数值格式的计算误差进行分析,Pirozzoli[16]提出了近似色散关系方法(Approximate Dispersion Relation, ADR),得到了激波捕捉格式的耗散和波数的关系。基于耗散误差大小应与色散误差相匹配的假设,Hu 等[17]提出了一种耗散与色散的关系,可以用于衡量计算误差的传播距离。Sun 等[18]根据Hu 等的耗散色散关系确定了格式中的耗散系数。最近,李妍慧等[19]提出了一种波数识别器,并基于此得到了一种根据局部流场的波数控制耗散的方法。
上述数值方法基于局部流场的光滑程度或者波数控制耗散,可以在提升大尺度流动结构分辨能力的同时有效地抑制小尺度非物理波动。然而,刘君等[20]发现5 阶WENO 格式在计算激波或接触间断时存在放大计算结果误差的风险,揭示了上述耗散控制方法的局限性。因此,不能简单地将如间断区域引入的非物理波动视为一种高波数的数值振荡。如何在稳定计算激波的同时降低耗散仍然是一个亟需研究的问题[21],这要求更加合理的耗散控制方法。
小尺度非物理波动不仅具有波数高的特点,同时具有幅值小的特点。为了更好地识别小尺度非物理波动,进而更精确地控制耗散,本文提出了一种采用局部流场的幅值和波数控制耗散的方法。
首先,针对如激波主导的或各向同性湍流的具有强烈非定常性的问题,根据一维非定常欧拉方程,确定小尺度下不同物理量之间的关系,并根据数值实验或Kolmogorov 尺度理论[22]确定小尺度波动幅值的阈值。根据所采用的人工黏性格式,推导了小尺度所对应的人工黏性通量幅值的阈值。通过比较人工黏性通量幅值的阈值与实际计算值,给出一种根据局部流场的幅值控制耗散的方法。
其次,基于傅里叶分析,构造了6 阶人工黏性的对称黏性。这个人工黏性仅有2 阶,在低波数区域耗散误差增长迅速而在高波数区域耗散误差增长缓慢。由于耗散误差与人工黏性通量的幅值相关,因此6 阶人工黏性通量和其对称黏性通量幅值的比值是一个4 阶小量。使用这个比值去控制6 阶人工黏性,就可以得到一个非线性的10 阶人工黏性。该人工黏性在中低波数区域耗散小,在高波数区域耗散迅速增大。
最后,同时采用上述2 种耗散控制方法,就可以针对小幅值或高波数的区域,采用较大的耗散来抑制小尺度的非物理波动。为了获得激波捕捉能力,将上述人工黏性格式与中心格式和TENO 格式进行混合,从而构造尺度可控的混合格式。
本文的具体内容如下,1.1 节介绍有限差分格式的理论基础;1.2 节讨论了非物理波动的幅值和波数;1.3 节推导并讨论了小尺度波动;1.4 节和1.5 节分别介绍波数控制与幅值控制;1.6 节介绍尺度可控的混合格式的实施方法。第2 节进行数值测试,验证所提出的格式具有很好的分辨率并可以有效抑制小尺度非物理波动。第3 节进行总结。
1 数值方法
1.1 理论基础
以一维双曲型方程组为例:
式中:Q为守恒变量;F为守恒通量;t为时间;x为空间坐标。
假定对式(1)在空间方向上使用均匀一致的网格Δx=xi-1/2-xi+1/2进行离散,则有
式中:L为守恒形式的空间导数算子;F为对数值通量h的高阶逼近。h可以隐式地定义为
对于欧拉方程,为了改善高阶格式的稳定性,通常使用左特征矩阵R-1将守恒变量和守恒通量投影到特征空间进行求解:
式中:q和f分别为特征变量与特征通量。为简单起见,在下文中用标量形式进行分析,记q和f分别为标量形式的变量与通量。
Kim 和Kwon[23]指出,迎风型 的WENO 格 式可以拆分成一个中心格式和一个非线性耗散项;之后,Sun 等[18]通过释放数值格式中的自由度,从而可以独立地优化色散和控制耗散;最近,Fu等[24]也提出了一套可以独立优化色散和耗散的框架,这些研究为独立地控制耗散提供了理论基础。在下文中,将数值通量拆分成中心通量和人工黏性通量:
1.2 非物理波动的幅值和波数
针对光滑区域中产生的非物理波动,Hu等[17]使用一种耗散色散关系去估计必要的数值耗散大小,其可以表示为
式中:ζ定性表示由于色散误差导致的数值伪波包可传播的网格个数;κ为波数;κr为修正波数的实部;κi为修正波数的虚部;ε=10-3为一个可容许的误差界限。式(6)中分子部分表示数值伪波包的群速度误差尺度;分母部分表示耗散数值伪波包所需要的时间尺度。当|dκr/dκ-1|~ε时,ζ~O(1) ,即数值伪波包的传播距离仅为个位数网格间距。注意到,色散误差主要集中在高波数区域,因此数值格式可以在中低波数区域保持较低的耗散,而在高波数区域引入较多的耗散,这就是基于波数控制耗散的思想。
然而,上述分析不适用于间断区域产生的非物理波动。为了说明这个问题,考虑一个仅存在一道间断的一维问题。当网格较密时,光滑区域的数值通量逼近精确值,即
式中:h(x)和(x)分别为标量形式的数值通量及其逼近;xs为间断所在位置。Casper 和Carpenter[25-26]发现,除非间断正好处于网格边界上,激波捕捉方法仅有一阶精度,与数值方法的设计精度无关。因此,在间断附近的数值通量的误差会远大于光滑区域,即
为简单起见,不妨假定数值通量的误差函数为一脉冲函数,其满足式(9)和式(10)。
对其进行傅里叶分析可以得到:
式中:F(·)表示傅里叶变换。式(11)的能谱为
其中:F*(·)为F(·)的共轭。因此,间断区域产生的非物理波动服从均匀一致的能谱,这些非物理波动会传播到并污染光滑区域的流动结构。这使得一系列中心型的激波捕捉格式或混合格式不再合理,因为它们在中低波数区域会完全恢复为中心型格式,缺乏对这部分非物理波动的抑制能力,最终形成大量的“数值湍流”。而迎风型激波捕捉格式尽管能更好地抑制间断区域产生的非物理波动,但容易抹平流动细节。上述分析仅仅是一个简单的包含激波的算例,对于更加复杂的问题,上述现象会更加严重,这说明了基于波数控制耗散的局限性。
另一方面,间断附近的计算误差主要由网格与间断不匹配或通量分裂格式所引起,可以视为一个小量。因此,可以定性认为数值计算中产生的非物理波动是小幅值或高波数的小尺度波动。
为了抑制小尺度非物理波动,本文采取幅值和波数分别进行控制。首先,在小幅值区域添加人工黏性,从而抑制间断区域产生的小幅值非物理波动;其次,在高波数区域增强人工黏性的耗散,从而抑制光滑区域产生的高波数非物理波动。
在此强调,欧拉网格下的激波捕捉方法必然会在间断附近产生非物理波动,上述耗散控制的目的在于减少非物理波动对光滑区域的影响,无法彻底消除该非物理波动。若要减少间断区域产生的非物理波动,需要加密网格或改用其他方法。
1.3 小尺度波动
如1.2 节所述,非物理波动往往是具有小幅值或高波数的小尺度波动。因此,当某局部区域物理量的波动幅值小于某一阈值时,可以认为该区域存在小尺度的非物理波动。为了得到小尺度非波动幅值的阈值,首先需要推导小尺度下物理量之间的关系。考虑一维非定常欧拉方程,将密度方程代入到动量方程中,可以得到:
式中:ρ为密度;u为速度;p为压力。在可压缩流动中,往往会出现如激波和湍流等复杂情况。针对这些具有强烈非定常性的问题,可以忽略式(13)中的定常部分ρu(∂u/∂x)的影响,得到小尺度下密度与速度波动之间的关系式:
式中:ρΔ、uΔ和pΔ分别为小尺度下的密度波动、速度波动和压力波动;τ和η为小尺度下的时间和空间;Ma为马赫数。
根据压力和密度之间的关系,可以得到:
式中:γ=1.4 为空气比热比;c为声速。若给定小尺度波动幅值的阈值为σ=uΔ/u,则只需根据所计算问题的给定其他特征量ρ、p、u、Ma,就可以估计出小尺度下的物理量波动ρΔ、pΔ、uΔ。易得,小尺度下的守恒变量为
其中:e为总能量。类似的,可以得到小尺度下的守恒通量FΔ以及特征空间的小尺度变量qΔ和通量fΔ:
根据这些小尺度下的物理量,可以识别出小幅值的非物理波动,从而更合理地控制格式的耗散并区分光滑区域和间断区域。具体实施过程见1.5 节和1.6 节。
本文重点考虑激波主导的问题和具有经典理论的各向同性湍流问题。对于不同问题,小尺度波动幅值的阈值可能会差别很大,因此需要采用不同的方法进行确定。
针对激波主导的问题,本文在2.1 节中通过正激波算例研究了阈值σ的敏感性。当阈值σ较大时,会导致对间断的误判;当阈值σ较小时,无法有效抑制小幅值的非物理波动。 考虑σ=0.1,其含义为小尺度的波动要比宏观量小一个量级。注意到,当σ在0.1 附近时,计算结果对σ并不敏感,因此对于所有激波主导的问题,均选取σ=0.1。
对于具有成熟理论的各向同性湍流问题,可以类比Kolmogorov 尺度与积分尺度的关系,根据所求解问题的特征参数得到网格尺度波动幅值的阈值σΔx,使用该阈值可以得到更精确的结果。
根据能量的耗散率和输运率应当相等的条件,基于量纲分析,Kolmogorov 尺度与积分尺度的物理量存在如下关系:
式中:ηk为Kolmogorov 尺度;ℓ 为积分尺度;Re为雷诺 数;uk为Kolmogorov 尺度的速度波动;ν为动力黏性系数;u为积分尺度的速度波动。为了将网格无法解析的小尺度非物理波动耗散掉,在网格尺度,数值的耗散率与输运率也应当相等。因此,对于网格尺度远大于Kolmogorov 尺度的情况,通过用Δx替代式(20)中的ηk,结合式(21),可以类比得到网格尺度下的速度波动uΔx与积分尺度的速度波动u之间的关系为
值得注意的是,式(22)并不代表数值计算中某波数区域内的速度遵从1/3 幂律,仅用于估计网格尺度下的速度波动幅值大小。此外,与波动能量的-5/3 幂律不同,上述推导没有用到惯性子区中流体黏性与耗散率相比是次要的这一假设[27-28]。唯一的假设为在网格尺度Δx附近,数值的耗散率和输运率应当匹配。
对于曲线坐标系下的问题,可以通过坐标变换得到式(16)~式(19)在计算坐标系下的对应物理量。然而,仍需进一步研究上述耗散控制方法对曲线坐标系下产生的坐标变换诱导误差[29]的影响。此外,对于高各向异性的湍流、强分离或转捩等复杂情形,仍需要根据数值实验或经典理论确定阈值σ,这将是接下来研究的重点。
1.4 波数控制
如1.2 节所述,非物理波动具有高波数的特点。因此数值计算中的高波数流动细节往往是非物理的,需要加以控制,本节采用波数对人工黏性进行控制。在Jameson 等的人工黏性方法[30]中,人工黏性的大小依赖于流动的光滑程度。然而这种方法容易对极值点产生误判。Sun[18]和Fu[24]等主要通过采用线性的人工黏性合理地控制黏性。对于6 点模板的通量格式,线性的人工黏性最高仅有6 阶,因此无法在对高波数区域产生足够耗散的同时较好地分辨中低波数流动细节。而基于傅里叶分析,可以构造出更高阶的人工黏性,从而在对高波数区域保持足够耗散的同时减少对低波数区域的耗散。首先,6 个模板点的线性人工黏性通量可以表示为
对κi进行求导可得
注意到式(25)中等号右边第2 项在κ∈(0,π]区间的积分为0,而第1 项和第3 项共同的系数共同决定波数κ=π 时的耗散误差。特别地,第2 项的系数可以用于调整耗散误差随着波数的增长速率在低波数和高波数的比例关系。对于5 阶迎风格式所对应的6 阶人工黏性,其系数为c1=1/60,c2-c1=-6/60,c3-c2=15/60 ,其耗散误差在低波数增长缓慢,而在高波数增长迅速。将式(23)中第2 项取反数,可以得到c1=1/60,c2-c1=6/60,c3-c2=15/60,其耗散误差在低波数增长迅速,在高波数增长缓慢。这种人工黏性作为6 阶人工黏性的对称黏性项,是一个耗散非常大的2 阶人工黏性。由于耗散误差与人工黏性通量的幅值相关,因此6 阶人工黏性通量和其对称黏性通量幅值的比值是一个4 阶小量。使用这个比值去控制6 阶人工黏性的通量,就可以得到10 阶精度的非线性人工黏性:
式 中:为10阶非线性人工黏性;为6 阶线性人工黏性为6 阶线性人工黏性的对称黏性;ε=10-40。
为了展示非线性人工黏性的特点,对各种格式进行傅里叶分析,其结果如图1 所示。与预期的一样,6 阶人工黏性的对称黏性和5 阶迎风格式的耗散误差具有对称性,标定过的1 阶迎风格式位于两者中间。10 阶非线性人工黏性的耗散误差在波数2.1 之前小于9 阶迎风格式,在高波数逐渐恢复到5 阶迎风格式。尽管傅里叶分析不能完全地展示非线性的影响,但上述分析仍有一定参考意义,后续的数值实验将展示10 阶非线性人工黏性对中低波数流动细节的保持和高波数非物理波动的控制能力。

图1 各种格式的耗散特性Fig. 1 Dissipation properties for various schemes
1.5 幅值控制
如1.2 节所述,非物理波动具有小幅值的特点。因此数值计算中幅值小于阈值σ的波动是非物理的,需要加以控制。注意到,6 阶人工黏性的耗散误差在波数<2π/5 时耗散误差比较小。因此假定一道波数为2π/5,幅值为A的小尺度波动正弦波。定义在不同相位下,6 阶人工黏性对于该正弦波计算出的最大值为过滤系数εf,易得
在保证光滑区域数值格式连续[31]的前提下,对10 阶非线性人工黏性进行幅值控制:
1.6 尺度可控混合格式
1.4 和1.5 节所提出的方法可以根据幅值和波数控制耗散,但是无法分辨出如间断的不光滑流动结构。为了获得激波捕捉能力,需要将上述方法与激波捕捉格式进行混合。在激波捕捉格式中,TENO 格式克服了WENO 格式在奇点处降阶的问题,往往具有更好的分辨率。因此,本文选用6 阶TENO 格式[12]进行混合,构造了尺度可控混合格式。TENO 格式继承WENO 格式的思想,其通量可以通过如下方法得到:

表1 子模板数值通量的系数Table 1 Coefficients of numerical flux of sub-stencils
在WENO-Z 的基础上,TENO 进行尺度分离:
式中:γk为尺度分离的光滑因子;τ6为以6 点模板计算的参考光滑因子;βk为每个子模版的光滑因子;ε=10-40是一个足够小的数,其作用仅为防止分母为0。根据Jiang 和Shu 的定义[5],光滑因子βk的计算式为
参考光滑因子τ6可以定义为
对γk进行无量纲化可以得到
式中:χk为无量纲化的光滑因子。
之后对χk进行截断从而区分光滑和不光滑的模板:
式中:δk为截断系数;CT为截断阈值,本文采取推荐值10-7。
最后,可以得到TENO 格式的非线性权为
式中:dk为理想权,具体为d0=9/20,d1=6/20,d2=1/20,d3=4/20。
当流动较为光滑时,6 阶TENO 格式的非线性权ωk与理想权dk相等,此时TENO 格式将会恢复到6 阶线性中心格式:
为了在更合理地控制耗散的同时获得激波捕捉能力,将基于幅值和波数的耗散控制方法与TENO 格式进行混合,构造了尺度可控混合格式。其数值通量为
式中:为混合格式的通量;下标“comp”和“char”指该通量是通过组份方向或特征方向重构得到的;Case 1 指在坐标方向判断为光滑的情况;Case 2 指在坐标方向判断为光滑、特征方向判断为不光滑的情况;Case 3 指在坐标方向和特征方向均判断为不光滑的情况。在这套混合格式结构中,坐标方向的混合可以免除特征变换和非线性格式的计算,从而提升计算效率;特征方向的混合可以最大程度上减少非线性机制的启动。特别地,坐标方向上仅使用密度进行判断,这进一步地减少了计算量。
是否光滑可以通过光滑指示器SI 和一个人为给定的阈值TH 判断。当SI<TH 时判断为不光滑,否则为光滑。本文所采用的光滑指示器是由Hill 和Pullin[14]提出的WENO形式的开关函数进行推广得到的,定义为
式(39)含义为计算任意相邻的3 个子模版的最小值和最大值的比值,这样做的目的在于防止模板增大时对光滑区域的误判。特别地,为了改善格式的数值对称性,将Jiang 和Shu 对βk的定义中所使用的积分区间改为[xi,xi+1]:
式中:子模版的选取与6 点WENO 格式相同。
此外,文献[14]推荐式(39)中ε=10-4。然而,文献[32]指出当ε较大时,会起到对光滑指示器进行截断的效果,这导致对于不同问题往往需要调整ε以获得最佳结果。为了规避ε的影响,在本文中,选取ε=10-40,并基于小尺度的幅值提出一种新的方法来替代ε的截断效果。
该方法的核心思想为将所有波动幅值小于阈值的小尺度非物理波动均视为光滑区域,并通过幅值控制耗散掉。因此假定一道波数为π、幅值为A的小尺度波动正弦波。定义在不同相位下,光滑因子βk的最大值为过滤系数εf,易得
因此,当式(42)的逻辑判断为真时,Case 1 判断为光滑。
最后,在坐标方向,阈值THcomp=1/4 设为一个非常保守的数;在特征方向,使用特征通量进行判断,阈值THcomp=1/14 使用Zhao 等[33]的推荐值(Hill和Pullin 的推荐值为1/150~1/120[14])。
为了更好地显示本文所提出的耗散控制方法的优越性,在此定义一种中心-TENO 混合格式。其与尺度可控混合格式在实施上的区别在于,不施加耗散和基于幅值的光滑判断。此外,ε取为文献[14]的推荐值ε=10-4,并随问题调整。
2 算例验证
为了展示基于幅值和波数的耗散控制方法的优越性,展示了4 个激波主导的标准算例和三维可压缩各向同性衰减湍流的计算结果。
其中,激波主导的无黏算例存在奇异性。即黏性越小,雷诺数越高,流动细节越丰富;一旦黏性为0,却“搓不出涡”了。由于激波捕捉过程需要一定的数值黏性,计算结果与数值方法的修正方程有关。因此数值黏性越小,修正方程的雷诺数越大,流动细节越多。这些算例的流动细节的丰富程度可以用于评估数值方法引入的数值黏性大小。
尽管修正方程不再无黏,但对于波后未受到影响的区域,涡量仍应当等于0。涡量的强度越小、旋涡的尺度越大,说明能更好地抑制小幅值或高波数的小尺度非物理波动。
针对激波主导的问题,特征物理量ρ、p、u、Ma选为波前波后参数的平均值。针对可压缩各向同性衰减湍流算例,密度和压力均取初始值,速度与积分尺度均取最大含能涡所在波数值。
所有格式均采用3 阶龙格-库塔法进行显式时间推进。坐标方向使用局部Lax-Friedrichs 矢流通量分裂格式。按照文献[13]中推荐的,特征方向使用Rusanov 矢流通量分裂格式。黏性项使用6 阶中心格式离散。
2.1 一维相对坐标系下的正激波
参考文献[20]中的正激波算例,计算域设置为[0,1],使用200个网格进行离散。激波运动速度为3.0。本算例固结于激波的相对坐标系下进行计算,激波位置固定在x=0.5处。波前波后参数为
计算时长为t=100 。由于在相对坐标系下,可以统计出所有相对位置物理量的最大值和最小值,从而可以更直观地比较激波在从初始间断演化成数值激波的过程中产生的非物理波动。
图2 研究了激波主导的问题对阈值σ的敏感性。图中,黑色、红色、蓝色线代表不同阈值σ的计算结果。实线为t=100 时刻的瞬时值;长虚线为整个计算过程中各点处物理量的最大值;点线为最小值。好的数值方法应当仅在初始间断附近形成一道数值激波,在远离间断的位置,物理量的最大值和最小值应始终与初始值保持一致。因此,图2 中的长虚线和点线可以代表非物理波动的传播与衰减过程。考虑σ=0.1,其含义为小尺度的波动要比宏观量小一个量级。数值实验的结果发现,σ≪0.1 时,对小尺度非物理波动的抑制能力下降;σ≫0.1 时,会在间断附近出现振荡。进一步实验发现,σ在0.1 附近时对数值实验的影响不明显。因此,对于激波主导的算例,σ=0.1 可以良好地区分光滑区域和间断区域并抑制小尺度的非物理波动。
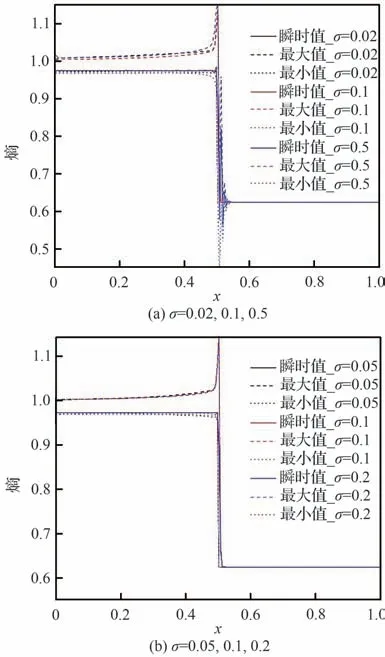
图2σ 对激波主导问题的敏感性Fig. 2 Sensitivity of σ to shock dominant problem
图3展示了各种格式产生的非物理波动。3 种格式均能得到稳定的激波结构,尺度可控混合格式的小尺度非物理波动略小于TENO 格式,远小于中心-TENO 格式。在远离激波处,尺度可控混合格式的计算误差依然存在衰减趋势;TENO 格式和中心-TENO 的计算误差在一定距离之后保持不变。这是因为TENO 和中心-TENO 格式仅依据光滑程度控制耗散,当非物理波动较为光滑时会退化为无耗散的中心格式,无法进一步加以抑制。而根据幅值和波数控制耗散不会受到非物理波动光滑程度的影响。

图3 计算过程中的最大值和最小值及t=100 时的数值激波Fig. 3 Maximum and minimum values in calculation process and numerical shock wave at t=100
最后,在激波附近区域,不同格式的非物理波动完全相同,这是因为各种格式均采用了相同的格式对间断进行捕捉。特别强调,本文无意于消除激波捕捉过程中产生的非物理波动,本文所提出的幅值和波数控制仅用于抑制已经产生的小尺度非物理波动的进一步传播。
2.2 激波密度波相互作用问题
现在考虑Shu 和Osher 提出的激波密度波相互作用问题[34],计算域设置为[0,10],使用200个网格进行离散,初始条件为
选取计算时长为t=1.8。一道马赫数为3的激波与密度波相互作用,并产生丰富的流动细节和间断。因此,该问题可用于检验对流动细节的分辨能力。其中,“精确解”由经典的5 阶WENO 格式使用4 000 个网格点得到。
如图4 所示,在密度波区域,中心-TENO 格式和尺度可控的混合格式均能更好地保持密度波的振幅。尺度可控的混合格式与中心-TENO格式的计算结果几乎相同,说明没有过多的引入数值黏性,可以有效改善对大尺度流动结构的分辨能力。而在间断区域,中心-TENO 格式在x=2.8 和x=3.6 均产生了数值振荡。而尺度可控的混合格式则完全避免了数值伪波。

图4 激波密度波相互作用问题的密度分布(t=1.8)Fig. 4 Density distribution of shock-density interaction problem (t=1.8)
2.3 二维黎曼问题
现在考虑Lax 和Liu 提出的二维黎曼问题[35],计算域设置为[0,1]×[0,1],使用400×400 个网格进行离散。边界条件均为狄利克雷边界条件,初始条件为
选取计算时长为t=0.8。每个域之间的差异导致许多复杂的现象,包括激波、稀疏波、滑移线。这些由激波相互作用引起的涡流非常适合测试数值方案的分辨率。理想的数值格式应该捕获更多由滑移线引起的开尔文-亥姆霍兹不稳定性以及它们在射流头部的复杂相互作用引起的涡流。除此之外,在未受到激波相互作用问题干扰的波后区域,流场物理量应当均匀一致,也就是说这些区域的涡量应当等于0。
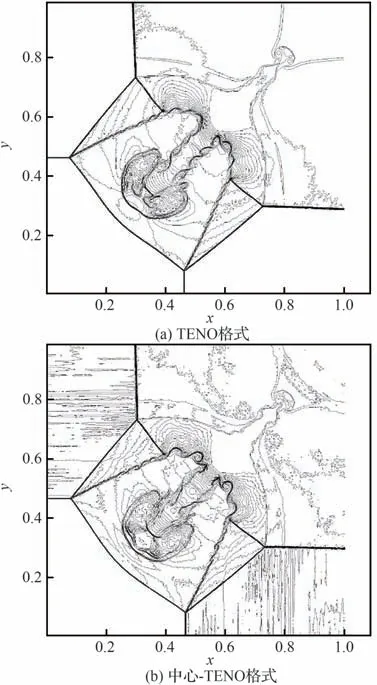
由图5 展示t=0.8 时的密度等值线可知,TENO格式,中心-TENO格式,尺度可控的混合格式均能捕捉到大量流动结构。相比TENO格式,中心-TENO 格式和尺度可控混合格式均能捕捉到更多的流动细节,且尺度可控混合格式捕捉到的流动细节更加丰富。结合图6中不同格式的涡量等值线可知,尺度可控混合格式在波后区域涡量等值线的密度更小,更符合物理规律。相比起中心-TENO格式,尺度可控混合格式减少了小尺度非物理波动对主要流动结构的干扰,增强了对光滑区域的识别能力。根据图7中2个混合格式的间断探测结果,可以发现混合格式在主要流动结构附近更少地启用TENO格式,因此更好地保留了流动细节。
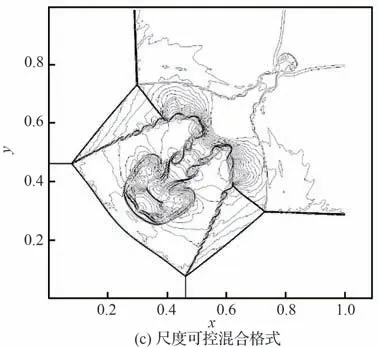
图5 二维黎曼问题t=0.8 时的密度等值线(在0.2~1.6 之 间33 等 分)Fig. 5 Density contours of 2-D Riemann problem at t=0.8(33 equally spaced from 0.2 to 1.6)

图6 二维黎曼问题t=0.8 时的涡量等值线(涡量=0)Fig. 6 Vorticity contours of 2-D Riemann problem at t=0.8(vorticity is equal to 0)
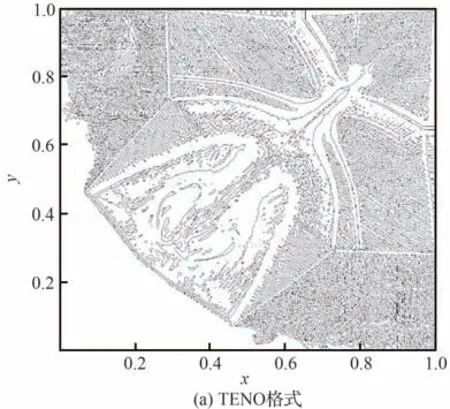
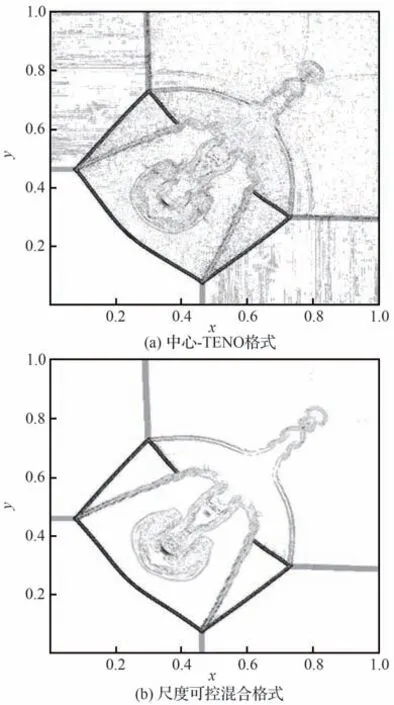
图7 二维黎曼问题t=0.8 时的间断探测结果Fig. 7 Discontinuous detection result of 2-D Riemann problem at t=0.8
另一方面,2 个混合格式在数值不对称性上也有一定的改进。混合格式在光滑区域减少了强非线性机制的启动,因此提升了数值对称性。最后,尺度可控混合格式给出非常干净的间断识别结果,这归功于小尺度波动的引入。
2.4 双马赫反射问题
现在考虑双马赫反射问题[36],计算域设置为[0,4]×[0,1],使用960×240 个网格进行离散。在本例中,一道马赫数为10 的激波以与x轴夹角为60°的方向向右移动,并与下壁面发生反射。入口和出口分别采用进口与出口边界条件。上边界采用精确的波前波后参数,并随着激波的移动而变化。在下边界,x∈[0,1.666 7]被设定为波后边界条件,其余部分被设定为反射边界条件。初始条件为
选取计算时长为t=0.2。同样的,在未受到激波相互作用问题干扰的波后区域,流场物理量应当均匀一致,即这些区域的涡量应当等于0。
由图8 展示t=0.2 时的密度等值线可知,在滑移线附近,尺度可控混合格式能捕捉到更加细致的流动结构。结合图9 中不同格式的涡量等值线可知,尺度可控混合格式很好地控制了激波演化过程中产生的小尺度非物理波动。

图8 双马赫反射问题t=0.2 时的密度等值线(在2~22之间33 等分)Fig. 8 Density contours of double Mach reflection problem at t=0.2(33 equally spaced from 2 to 22)

图9 双马赫反射问题t=0.2时的涡量等值线(涡量=0)Fig. 9 Vorticity contours of double Mach reflection problem at t=0.2 ( vorticity is equal to 0)
根据图10 中的间断探测结果,尺度可控混合格式再一次给出非常干净的间断识别结果,说明尺度可控混合格式可以在不降低分辨率的前提下控制小尺度非物理波动并识别光滑区域。

图10 双马赫反射问题t=0.2 时的间断探测结果Fig. 10 Discontinuous detection result of double Mach reflection problem at t=0.2
2.5 可压缩各向同性湍流衰减问题
考虑可压缩各向同性衰减湍流算例[37],计算域设置为[0,2π]×[0,2π]×[0,2π],网格分辨率为64×64×64。初始泰勒马赫数为Mat=0.6,初始雷诺数Reλ=100,与文献[37]中相同。采用周期性边界条件。设定初始湍能谱为
式中:urms为速度均方根;κ0为峰值波数,本文取4。选取计算时长为t/τ=4,τ=2/(κ0urms)。在本算例中,存在最大含能涡,因此将积分尺度设定为最大含能涡尺度ℓ=2π/κ0。
图11展示了计算过程中速度、涡量、温度的无量纲2 范数的变化曲线与DNS(Direct Numerical Simulation)结果的对比。可以看到,在计算的前期,如t/τ<1 时,尺度可控混合格式的耗散与其他格式的相当。当t/τ>1 时,随着湍流衰减的演化,流场中高波数流动增加,TENO 和中心-TENO 格式的耗散显著增加,而尺度可控混合格式仍然保持了较低的耗散。尺度可控混合格式与DNS 的计算结果吻合良好,说明网格尺度的推导可靠,在数值计算中起到湍流模型的作用。

图11 可压缩各向同性衰减湍流的计算结果Fig. 11 Calculation results of compressible isotropic decaying turbulence
2.6 非物理波动尺度
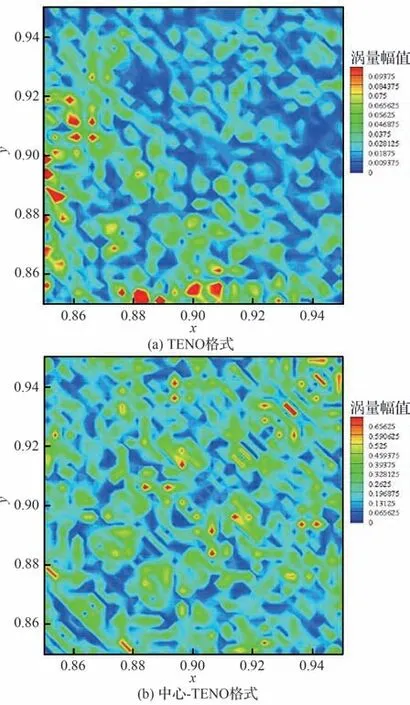
为了进一步验证本格式对非物理波动的控制效果,研究非物理波动的幅值和长度尺度。因为2 个二维算例的计算结果相似,选择二维黎曼问题中t=0.8 时刻在区域[0.85,0,95]×[0.85,0.95]处的涡量进行研究。这个区域作为波后区域,理想情况下的涡量应当为0。图12给出涡量幅值的云图。可以看到,在该区域,TENO 格式的计算误差不到0.1,中心-TENO格式的计算误差不到0.7,尺度可控混合格式计算误差不到0.004。图13展示涡量为0 的等值线和网格的放大图。可以看到,TENO 格式和中心-TENO 格式均呈现随机混沌状的小尺度非物理波动,而尺度可控混合格式的非物理波动呈条带结构。其次,TENO 格式的非物理波动尺度大约在4个网格长度左右,而中心-TENO 格式在2个网格长度左右,尺度可控混合格式的波动尺度在8~10 个网格左右。事实上,这是因为中心-TENO 格式和TENO 格式仅依据光滑程度控制耗散,因此会把小幅值的非物理波动视为光滑区域。此时,2个格式均会恢复为无耗散的中心格式,因此难以抑制具有小幅值和高波数特点的小尺度非物理波动。
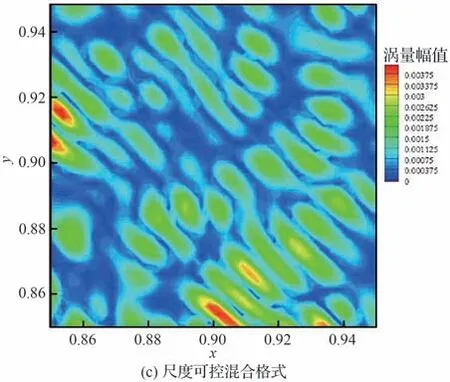
图12 波后区域涡量幅值云图的放大图Fig. 12 Enlarged view of vorticity magnitude contours in post-shock region
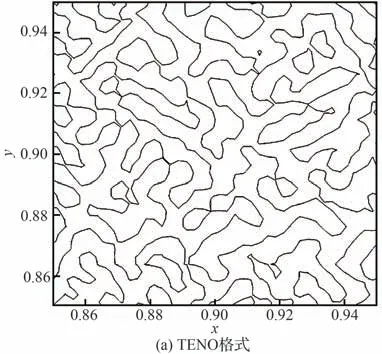
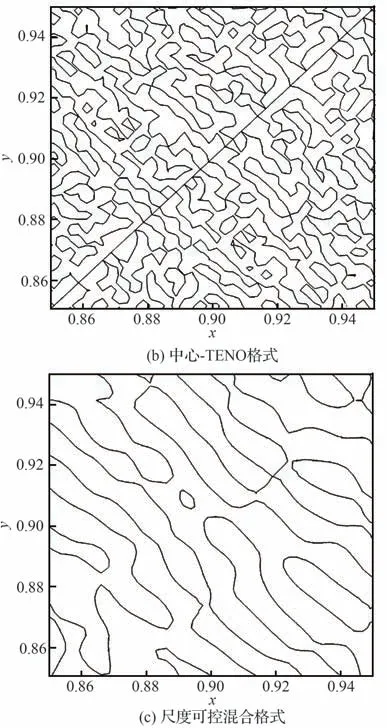
图13 波后区域的涡量等值线放大图和网格Fig. 13 Enlarged view of vorticity contours and mesh in post-shock region
图12和图13 表示,简单的基于光滑程度控制耗散无法有效抑制小尺度非物理波动;而基于幅值和波数,可以更好地抑制小尺度非物理波动。
2.7 计算效率
2.1 节~2.5 节的计算结果已经展示了尺度可控混合格式对间断的识别能力。本节对比了3 种格式的计算效率。表2 展示了2 种混合格式在计算过程中使用的TENO 格式的比例。可以看到,对于激波主导的算例,尺度可控混合格式的TENO 使用比例在3.2%左右,而中心-TENO 格式的使用比例在6.5%左右,尺度可控混合格式略好。而在三维算例中,尺度可控混合格式的TENO 使用比例仅为0.1%,而中心-TENO 格式的使用比例高达31.7%。
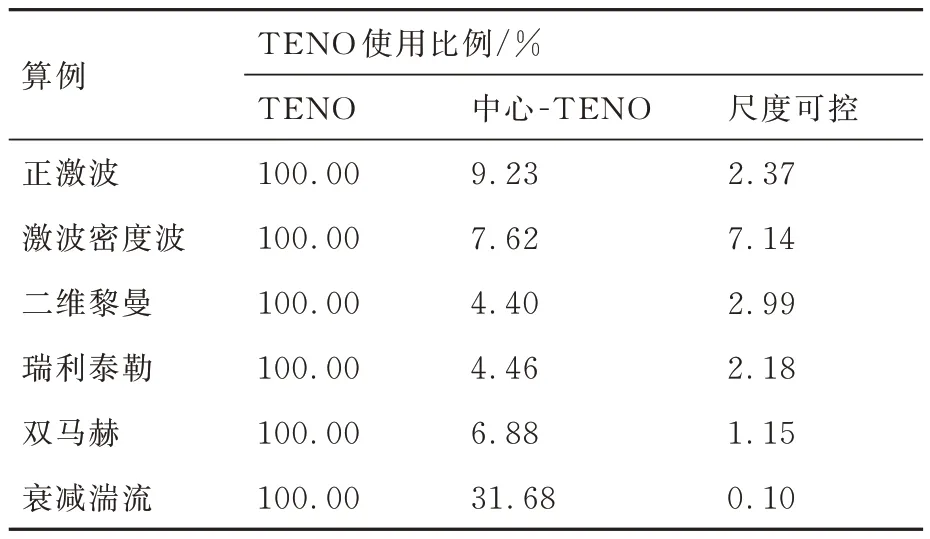
表2 TENO 格式的使用比例Table 2 Usage ratio of TENO scheme
除了基于Kolmogorov 尺度推导的网格尺度波动幅值的阈值更加合理之外,导致上述现象的还有以下原因。首先,可压缩衰减湍流不是激波主导的,同时还是一个三维算例,因此激波占比更低。其次,基于幅值和波数可以有效抑制小尺度非物理波动,从而确保大多数区域被识别为光滑的。最后,随着时间的推进,流场中高波数的流动结构增加,传统的开关函数容易对高波数的流动结构产生误判,而使用小尺度幅值辅助的开关函数不受流动结构波数的影响。
表3 统计了不同算例的计算时间。尽管由于编程手段的差异,计算时间不能完全表示算法的计算效率,但仍有一定借鉴意义。首先,尺度可控混合格式与中心-TENO 格式的计算效率接近。尽管尺度可控的混合格式更少地使用了TENO 格式,但是增加了程序复杂程度。此外,尺度可控混合格式计算效率为TENO 格式的2~4 倍。随着计算问题维数的增加,程序复杂性的增强,混合格式所带来的效率提升被程序中的其他模块逐渐稀释。通过对程序进行优化,尺度可控混合格式的计算效率提升幅度会更大。
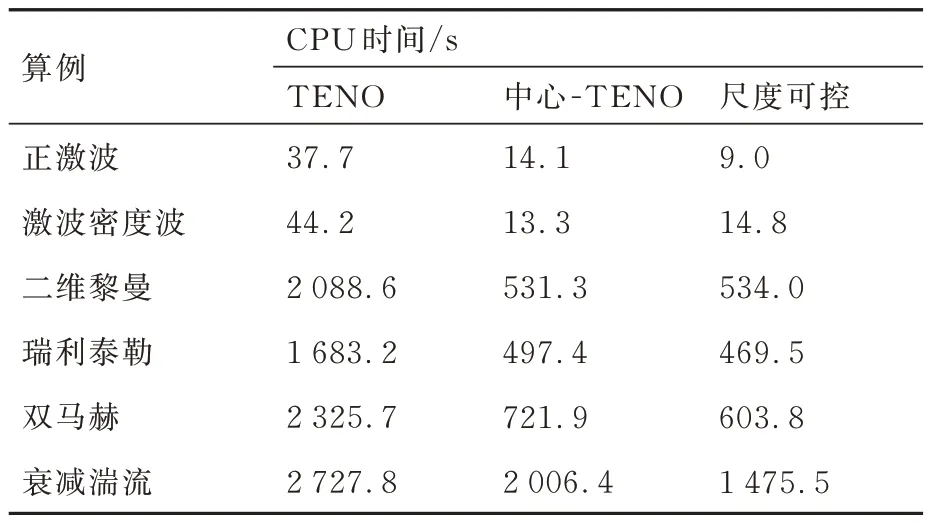
表3 不同算例的计算时间Table 3 Calculation time of different cases
3 结 论
本文提出一种基于幅值和波数控制耗散的方法。为了获得激波捕捉能力,与TENO 格式进行混合构造了尺度可控混合格式。主要结论如下:
1)对于激波主导的或各向同性湍流的具有强烈非定常性的问题,根据一维非定常欧拉方程,推导了小尺度下不同物理量之间的关系,并通过数值实验或Kolmogorov 尺度理论确定小尺度波动幅值的阈值。基于该阈值构造了耗散大小和局部流场幅值的关系,从而有效抑制小幅值的非物理波动。一维正激波的结果表明,非物理波动的幅值显著减小。激波密度波相互作用算例中,在间断区域避免了数值振荡。二维算例(以二维黎曼问题为例)在波后区域的涡量分布表明,本格式在波后区域的涡量计算误差不到0.004,远远小于TENO 格式的0.1 和中心-TENO 格式的0.7。
2)基于傅里叶分析构造了10 阶非线性人工黏性,其耗散误差在波数2.1 之前小于9 阶迎风格式,在高波数逐渐恢复到5 阶迎风格式。二维算例在波后区域的涡量分布表明,尺度可控混合格式减少了非物理的数值湍流,其非物理波动的尺度在8~10 个网格左右,远远优于TENO 格式的4 个网格和中心-TENO 格式的2 个网格。
3)基于小尺度的幅值提出一种新的方法替代ε在开关函数中的截断效果,改善了对光滑区域的识别能力。在整个计算过程中,尺度可控混合格式平均仅有3.2% 左右的情况下启用TENO 格式,而中心格式有6.5%左右的情况启用TENO 格式。相较于TENO 格式,尺度可控混合格式效率提升2~4 倍。
4)对于本文中的算例,尺度可控混合格式可以捕捉到更多的大尺度流动细节。激波密度波算例中更好地保持了密度波的幅值。可压缩各项同性衰减湍流算例与DNS 结果对比良好。即使相对于中心-TENO 格式,尺度可控混合格式分辨率也有所提升。

