以“学生提问”撬动深度学习

张齐华

摘要：鼓励、引导学生提出问题，并且基于学生提问展开数学教学，有利于引发学生的深度学习。《轴对称图形》一课，以学生提问为支点，通过前置学习任务中的独立提问、小组共同学习中的相互提问、全班组际对话中的互动答疑等学习活动，激发学生主动参与、充分卷入学习，撬动深度学习。

关键词：小学数学；提出问题；学生提问；深度学习；《轴对称图形》

*本文系江苏省教育科学“十四五”规划课题“促进儿童社会性素养发展的‘社会化学习’范式建构”（批准号：SJMJ/2021/03）的阶段性研究成果。

所谓“深度学习”，是指“在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程”［1］。鼓励、引导学生提出问题，并且基于学生提问展开数学教学，是触发学生深度学习的有效路径。一方面，学生有价值的提问，往往发生在已知与未知的交界处，发生于“最近发展区”，对学生而言具有适切的思维挑战，容易激发学生的好奇心和求知欲。另一方面，由于推动课堂前行的问题不再由教师主导，也并非来自教材、教参等课程文本，而是来源于学生自己。这样的问题与学生息息相关，更容易引发学生的探究兴趣和思考乐趣，激发学生的学习主动性。最后，当学生提出的问题经过独立思考或同伴互助，最终由学生自己解决时，这样的成功体验是解决教师提出的问题所无法比拟和替代的。因而，由学生提问展开的数学学习就具备了深度学习的特质。

近几年来，笔者带领小学数学团队开展的“社会化学习”课堂变革实践，正是以“学习地图”为载体，以“小组共学”为路径，以“组际答疑”为核心，借助“学生提问”这一关键因子，通过“前置学习任务中的独立提问”“小组共同学习中的相互提问”“全班组际对话中的互动答疑”这些连续性的学习活动，着力撬动课堂中学生的深度学习。本文介绍一个具体案例。

一、教学过程

（一）独立探索，在深度研究中引发个体提问

师（出示学习单）课前，同学们独立完成了这个学习单，提出了学习过程中属于自己的问题。比如，有同学提出：“除了对折，还可以用什么更快捷的方法判断一个图形是不是轴对称图形？”有同学提出：“轴对称图形可以有两条对称轴吗？”有同学提出：“学习轴对称图形有什么用？”……看得出来，大家在独立研究的过程中，既形成了自己对轴对称图形的初步理解，也产生了很多新的困惑。在老师看来，这就是有意义的学习，也是有深度的学习。为大家“点赞”！

学习单的内容如下：

【我的目标】

1.能判断日常生活中的对称现象，通过折一折、剪一剪、比一比等活动，认识轴对称图形，认识对称轴。

2.能通过看一看、折一折、比一比、想一想，判断一个图形是不是轴对称图形。

【我的研究】

1.图1中的哪些现象是“对称”的？在（）里打“√”。

你是怎么判断的？把你的想法写下来。

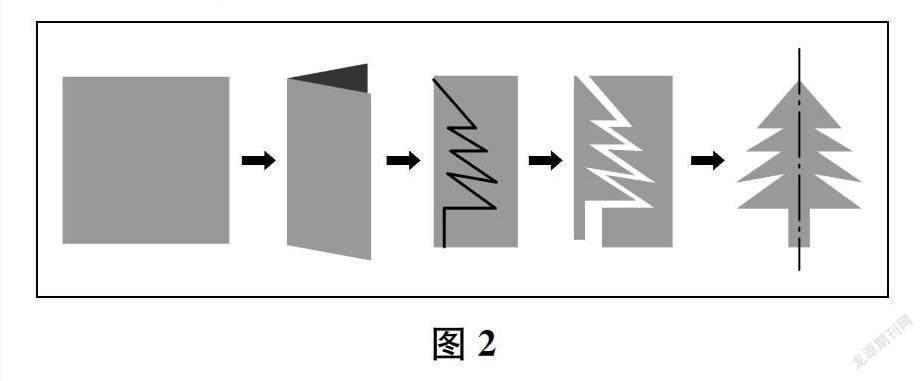
2.把一张纸对折后，照样子（如图2）画一画、剪一剪。

（1）剪下的图形是一个轴对称图形。对折时，折痕所在的线是它的对称轴。

（2）你能像这样，折一折、画一画、剪一剪，剪出3个不同的轴对称图形吗？

记得把作品带到课堂上来，和同伴说一说你是怎么剪的，它们的对称轴在哪里。

3.图3中的五个字母，哪几个是轴对称图形？在（）里打“√”，并说明理由。

4.关于今天的学习内容，你还能提出什么问题？

学习单给出了本节课基本的学习目标和指引学生完成学习目标（探索新知识、建构新理解、生成新经验）的学习任务。学生在独立完成学习单的过程中，由于经验、思维与能力的不足，自然会产生认知失衡，也就能提出自己的问题。

（二）组内交流，在持续对话中生成小组提问

师接下来，请大家在小组中先分享自己的思考，再帶着自己的问题碰撞交流。组内解决不了的问题，或产生出的新问题，可以提交全班进行讨论。

（学生小组交流，持续约15分钟。教师巡视。）

一个四人学习小组的交流过程如下：

生（1号）今天，我们讨论的内容是轴对称图形，我们先来看学习目标。（解读学习目标）接下来，我们来看“我的研究”第1题的第一个图形。谁来说？

生（4号）第一个图形是轴对称图形。如果拿笔画一画，它的中间有一条对称轴。

生（2号）大家还有别的方法来判断吗？

生（1号）如果把这只蝴蝶剪下来，对折一下，两边应该是一样的，所以它是轴对称图形。

生（2号）我来总结一下：只要找到对称轴，或者折一折两边重合，就可以认为这个图形是轴对称图形。第二个图形，谁来说？

生（1号）它是轴对称图形。把这片树叶左右对折，两边完全一样。

生（3号）我还有一种方法。我在树叶的中间画一条竖线，发现它正好是树叶的对称轴，所以我认为它是轴对称图形。

生（2号）我想补充一下：这里画的不是一条直线，应该这样画。（示范画点划线）第三个图形，谁来说？

生（3号）我觉得它不是轴对称图形。虽然外面的圆圈是对称的，但里面的字母不是对称的。

生（4号）因为它不能平均分成两半。你看，假如从中间画一条直线，它的两边是不对称的。

生（2号）最后一个图形，我来说吧。我觉得它是轴对称图形。把它从中间对折，它的两边应该会重合，所以它是轴对称图形。接下来，我们看一下第2题。谁来展示自己的作品？

生（4号）我的作品是一个京剧脸谱，它是轴对称图形。

生（2号）你是怎么剪出来的？

生（4号）我先把它对折，然后只要剪一边，它的两边就都出来了。中间的折痕就是它的对称轴。

生（3号）我剪的是一个杯子。我的方法和他差不多，也是先对折，然后只剪了一边，就剪出来了。

生（1号）我剪了一个南瓜脸。我先把一张纸对折，然后画了半个圆；剪完以后，再给它画上眼睛和嘴巴。它是轴对称图形。

生（4号）我想补充一下：画眼睛和嘴巴的时候，两边一定要一模一样。

生（2号）最好是在对折后，先把一只眼睛和半张嘴画好，这样剪出来的图形，才能保证是轴对称图形。

生（3号）我剪的是一个长方形，我觉得长方形就是轴对称图形。

生（1号）我有质疑。你在长方形的右边写了你的姓名，这样两边就不对称了。所以，长方形上最好不要写姓名。

生（2号）如果要写姓名，左边和右边要写同样的姓名，左边的字还要反着写。

生（3号）谢谢你的提醒。

生（2号）我剪的是一个胡萝卜。我先拿一张彩纸，把它对折，然后用铅笔画出胡萝卜的半边，把它剪下来，就成了一个完整的胡萝卜。大家同意吗？

生（齐）同意！

生（2号）那么，我们来说第三题吧。第一个字母，谁来说？

生（1号）它是轴对称图形。因为它的上面和下面是完全一样的，可以重合。

生（3号）我有质疑。它竖着看，左右两边没法重合啊。

生（4号）我有个提醒：只要能分成一样的两半，它就是轴对称图形，不管它是左右分的，还是上下分的。

生（2号）我觉得有道理。那第二个字母，谁来说？

生（4号）第二个字母是轴对称图形。虽然它横着、斜着对折都不能重合，但它竖着对折后两边完全重合，所以它是轴对称图形。

生（2号）我在第三个字母上画了六条线，横着、斜着、竖着都不能重合，所以它不是轴对称图形。

生（3号）我有补充：如果“S”上面的半圆和下面的一样，那它就是轴对称图形了。

生（1号）我没听懂你的意思。

生（3号）我是说，如果这个字母变成“3”的样子，那它就是轴对称图形了。

生（2号）有道理！第四个字母，谁来说？

生（3号）第四个字母是轴对称图形，虽然它上下对折不能重合，但是它左右对折能重合。

生（1号）最后一个字母不是轴对称图形。因为它不管左右对折，还是上下对折，哪怕斜着对折，都不能完全重合。

生（2号）大家说得非常好！我来总结一下。判断一个字母是不是轴对称图形，不能只看一个方向，而要多试几个方向。只要有一个方向上对折后能重合，它就是轴对称图形。最后，让我们交流一下自己提出的问题吧。

生（1号）我提的问题是：学习轴对称图形有什么用？

（没有同伴解答。）

生（2号）既然没人解答，那我来说说我提的问题：汉字、字母、数字、图形旋转半圈，能重合吗？

生（齐）什么意思？

生（2号）比如字母“C”，旋转半圈后，能重合吗？

生（1号）可以重合。只要是轴对称图形，不管旋转到哪个方向，都可以重合。

生（2号）不对！你看字母“T”，旋转半圈后，上面一横转到下面了，没法重合了。

生（4号）但是，字母“S”是可以的——旋转半圈后，它是能够重合的。

生（2号）看来，有些字母、图形旋转半圈能重合，有些不能。下面讨论谁提的问题？

生（3号）我带来了两个问题：轴对称图形在生活中有什么用？轴对称图形对生活有什么帮助？

生（2号）你这两个问题是一样的呀！一个意思。而且，和前面同学的问题也很像，没法解答。

生（4号）我来说一下我的问题：轴对称图形可以有两条对称轴吗？

生（3号）当然可以。

生（2号）不信的话，我现在给你画一个。（画出一个长方形）你看，这是一个轴对称图形吧。它横着对折，竖着对折，都能够重合，所以它有兩条对称轴。

生（2号）现在看来，1号和3号同学的问题没人能够解答，我们小组就写这个问题了。

（组长把1号和3号同学的问题写在便签条上，交给教师。）

在组内共学中，学生可以初步交流各自的思考，从而提升认识，形成共识。同时，也能初步交流各自独立研究时遇到的问题。这时，部分问题可以得到解答，部分无法解答的问题则成为小组的公共问题，为下一阶段组际之间的答疑互动提供了素材。

（三）组际答疑，在深度联结中深化数学理解

师老师转了一圈，发现我们班几乎每一个小组都能在组长的带领下进行有效交流，有对话、有追问、有回应、有总结。这才是小组交流应该有的模样。当然，组内交流后，各个小组也在个体提问的基础上，提出了代表小组的问题。我们一起来看一下。（汇总出示各个小组提出的问题，如图4所示）快速浏览各个小组提出的问题，你能读懂别的小组的问题吗？

（学生快速浏览。）

师细心的同学一定已经发现，这些问题大概可以分为这样几类。先看第一列：如何判断是否对称？怎样找对称轴？三角形一定是轴对称图形吗？对称轴能斜着吗？怎么剪轴对称图形？这是一组能够帮助我们更好地理解轴对称图形的问题。再来看第二列：轴对称图形只有一条对称轴吗？正方形有几条对称轴？正六边形是不是轴对称图形？圆有几条对称轴？这些问题都指向对称轴的条数，尤其是我们熟悉的平面图形究竟有几条对称轴。它们都是好问题！继续看第三列，前两个问题的视角已经从数学转向现实生活了：生活中有轴对称图形吗？学了轴对称图形有什么用？最后一个问题更有深度：除了轴对称，还有别的对称类别吗？这个小组显然不满足于研究轴对称了，还想向数学学习的更深处挺进。真好！接下来，我们就按从易到难的顺序，集中全班的力量，一起来回应这些问题。好吗？

生好！

师如何判断一个图形是不是轴对称，或者是不是轴对称图形？怎样找它的对称轴？对这一组问题，是直接回应，还是先在小组里二度讨论？

生直接开始。

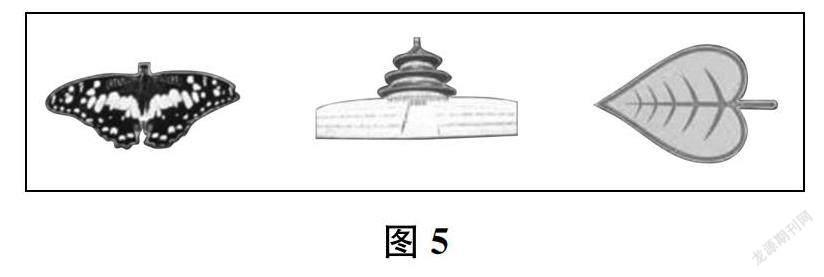
师（板贴，如图5所示）黑板上，老师正好贴了三个生活中的图案。它们是轴对称图形吗？谁能代表你们小组，和大家分享你们的观点？

生我觉得这里的蝴蝶、天坛、树叶都是轴对称图形。

师台下的同学如果同意，请一起拿手比画一下，它们的对称轴究竟在哪里？

（学生比画。）

师奇怪，这里的对称轴，有些是竖着的，有些是横着的，那会不会出现斜着的？

生会。（把树叶图旋转45度）这时，树叶的对称轴就是斜着的。

师看来，轴对称图形的对称轴的方向不只有横着或竖着的，也可以是——

生斜着的。

生我有补充。轴对称图形的方向发生变化，对称轴的方向也会跟着变化。

师聊着聊着，第8小组的问题也被我们顺便解决了。那你们是怎么判断一个图形是不是轴对称图形的？

生可以用眼睛看。如果一个图形的左右或上下两部分是完全一样的，那它就是轴对称图形。

师观察，的确是判断的一种好方法。

生我觉得看有时不准，我们可以用对折的方法来判断。比如，我们把天坛图从中间对折一下，它的左右两边重叠在了一起，所以它是轴对称图形。

师是部分重合还是完全重合？

生完全重合。

师看来，对折是一种更专业的方法。讨论到现在，第1小组的前半个问题已经有答案了，那后半个问题呢？

生我觉得对称轴就在对折的地方。

师数学上，折痕所在的这条直直的线，就叫对称轴。（示范画对称轴）现在，第1小组的问题讨论完毕。而第2小组显然并不满足于如何判断一个图形是不是轴对称图形，他们想知道究竟应该如何剪出一个轴对称图形。谁有好办法？

生其实，学习单已经告诉我们怎样剪出一个轴对称图形了。

师打断你一下：如果让你用三个字来概括一下剪轴对称图形的方法，你会选择哪三个字？

生（略作思考）我觉得应该是折、画和剪。也就是先把长方形纸对折，再画出轴对称图形的一半，最后沿着画好的线把图形剪下来，就可以得到一个轴对称图形。

师老师这儿就有一张白纸，你愿意向大家现场演示一下如何用“三字口诀”得到一个轴对称图形吗？

（学生上台演示。教师相机完成板书，如图6所示。）

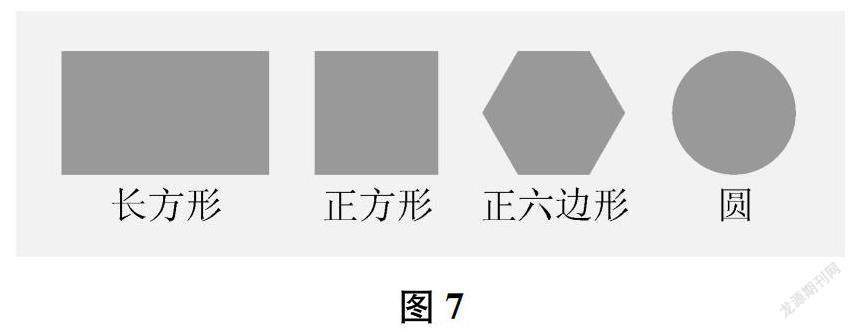
师解决完前两个相对比较基础的问题后，来看大家特别感兴趣的第二列提问：对称轴只有一条吗？长方形、正方形、圆等是不是轴对称图形？又有多少条对称轴？（出示图7）老师提前准备了这几个图形，谁能结合这些图形，具体回应一下这几个问题？

生我觉得，有些轴对称图形只有一条对称轴，比如之前的三个图形。但有些图形有两条对称轴，比如长方形。

生我反对！（上台同步比画）我觉得长方形有四条对称轴。师出现两种不同的觀点了。怎么办？

生大家看，我们的学习单就是一个长方形。我觉得，（横着对折后指着折痕）这是它的一条对称轴，（竖着对折后指着折痕）这也是它的一条对称轴，所以它有两条对称轴。

你漏了两条对称轴：长方形中，还有两条斜着的对称轴。

生我觉得斜着的两条不是对称轴。

师长方形到底有几条对称轴？谁能从板书中找到判断的依据和方法？

生我们可以把长方形折一折。大家看，（同步演示）如果把长方形横着对折或竖着对折，两边都可以完全重合；但是，如果把长方形斜着对折，两边不能完全重合。

师看来，判断一个图形是不是轴对称图形，或者判断它有几条对称轴，光靠看还不行，有时还得动手折一折、比一比。现在，你能确定长方形有几条对称轴了吗？

生两条。

师那正方形、正六边形和圆又有几条对称轴呢？如果大家的观点不一致，我们将再次通过折一折、比一比来判断。

生我觉得正方形有四条对称轴，它们就像一个“米”字一样。

生我觉得正六边形有三条对称轴，一条竖着的，两条斜着的。

生不对，正六边形应该有六条对称轴。

（该生上台比画，台下同学掌声通过。）

生我觉得圆有无数条对称轴。

生无论从哪个方向对折，圆的两边都能完全重合，所以圆有无数条对称轴。

师判断这些平面图形是不是轴对称图形、有多少条对称轴，应该是小学高年级才探讨的话题。然而，正是因为大家的主动提问，我们才有机会在二年级时就对这些话题有了初步的思考。当然，到了高年级，我们会继续就这些话题展开更深入、更专业的研究。接下来，敢不敢研究更有挑战性的问题？

生敢！

师除了轴对称之外，还有没有别的类型的对称？

生有！中心对称。

师（板书：中心对称）能不能告诉大家，你是从哪儿知道中心对称的？

生我在课前查阅了资料。比如，圆就是中心对称图形。

生我也查阅了资料，把一个图形旋转半圈后，如果和原来的图形完全重合，它就是中心对称图形。

师大家是有备而来啊！那么，学习单上的五个字母中，有没有中心对称图形？

生我觉得字母“S”就是中心对称图形。

生我想向大家演示一下。（上台同步演示）把字母“S”绕着中间这一点旋转半圈，正好和原来的字母完全重合，所以它的确是中心对称图形。

师除了“S”以外，26个字母中还有中心对称图形吗？黑板上的四个平面图形中，哪些也是中心对称图形？带着这些新问题，让我们课后继续展开研究。最后，让我们聚焦今天这节课的最后一个问题：生活中，你见到过轴对称图形吗？

（学生小组讨论后汇报——）

生我们佩戴的红领巾，就是轴对称图形。

生教室的窗户由两个相同的部分组成，它也能看作轴对称图形。

师当我们带上数学的眼光观察现实世界时，生活中随处都能看到轴对称图形的影子。老师课前也找来了一些生活中的画面，你能从中看到轴对称图形吗？如果能，用手比画一下它的对称轴。

（教师出示图片，学生一一判断并比画。）

师课的最后，老师也为大家留下一个问题：为什么生活中大量的建筑、剪纸、京剧脸谱等都设计成轴对称图形？这背后的原因到底是什么？让我们带着问题走进课堂，再带着新的问题离开课堂。

在组际交流中，由于每一个问题都是小组成员共同推荐的，加上教师精准的介入、引导与点拨，学生原有的模糊理解、肤浅表达、零散认知等不断得到澄清、深化与结构化。更有深度的学习正是在这样的组际互动与教师引导中得以发生。

二、教学反思

回顾完整的課堂学习历程，不难发现：“学生提问”的确是撬动学生深度学习的有效抓手。

首先，经由充分的训练与实践，学生完全具备提出问题、提出高质量问题的能力。他们所提的问题并不局限于依托数量关系所构想的常规数学问题，而能将触角伸向数学学习的关键处，指向思维的不足处。课例中，学习单呈现的轴对称图形的对称轴基本都是横平竖直的，学生由此提出“对称轴可以斜着吗”；当学生发现长方形、正方形永远都是轴对称图形后，便提出了“三角形一定是轴对称图形吗”；当整个学习单都要求研究轴对称图形时，学生提出“除了轴对称，还有别的对称类别吗”……这样的提问，不落俗套，真正反映了学生思维的盲区，指向数学学科的本质。

其次，学生自主提出的问题数量众多、难以预设，在讨论过程中还会生成新的问题，这给教师的课堂调控带来了巨大的不确定性和挑战。对此，一方面，教师需要提前了解学生自主提出的问题，做到心中有数、未雨绸缪；另一方面，面对学生小组共学后涌现的团队提问，教师要能快速进行甄别、分类、排序、整合，并且就若干核心问题如何引导学生展开讨论、如何促发学生深度思考，作出提前预判和有效规划。课例中，各小组看似提出了10个不同的问题，然而，只要对这些问题稍加梳理与归类，便不难发现，它们主要涉及“如何判定和创作轴对称图形”“如何判定对称轴的条数”和“轴对称图形在生活中有怎样的应用”这三个维度。由此，教师得以从纷繁复杂的问题碎片中抽身出来，而将所有精力聚焦到这三个被各个小组普遍关注的核心、关键问题上，并由此引导学生展开新的讨论。当然，这对教师的临场应变能力提出了更高的要求，也对教师的备课能力提出了新的期待，包括对数学知识的本质要有准确理解，对课程内容的重难点要有深刻洞见，对学生学习的经验起点、思维路径和方式要有精准把握，对如何基于“学生提问”把他们的思维与认识由模糊引向清晰、由肤浅引向深刻、由单一引向多元、由零散引向结构等要有清晰的规划。

最后，教材与教参预设的问题往往基于“教的逻辑”，基本规定了课堂可触及的边界。而由“学生提问”引领的数学课堂更侧重于“学的逻辑”，关注学生的真实困惑和学习体验，关注学生的好奇心和求知欲。学生的提问会面向所有的未知世界展开，这决定了课堂的原有边界会被打破，课堂将向四面八方打开。这样的课堂固然会因为充满未知和不确定性而让教师深感不安，但同样会因为开放性和生成性而展现出独特的吸引力。在这样的课堂中，只要是有价值的问题、能引发学生深度思考的问题，都可能成为大家共同讨论的焦点。课例中，原本并不属于这堂课的“三角形一定是轴对称图形吗？”“长方形、正方形、圆等是不是轴对称图形？各有多少条对称轴？”“除了轴对称以外，还有别的对称类别吗？”等问题便纷至沓来，进而，因为未知和不确定性而带来的探究乐趣、思维乐趣便一点点被点燃。正是在这样的教学逻辑中，“学生提问”真正让学习成为一场知识的历险，成为一次面向未知的深度探秘，高品质的深度学习便有可能真正发生。

参考文献：

［1］ 郭华.深度学习及其意义［J］.课程·教材·教法，2016（11）：2532.