大跨度预应力混凝土连续刚构桥跨中下挠原因分析

黄 炜， 余 健， 李晓猛， 李 懿， 宁德飚

(云南省公路科学技术研究院， 昆明 650051)

大跨度预应力连续刚构桥由于其优越的结构性能，在中国的桥梁建设中广泛应用。而在大跨度预应力连续刚构桥迅速发展的同时，其病害也在运营过程中不断出现，尤其是跨中长期过度下挠、开裂等病害影响其运营安全，威胁到了桥梁的正常使用性能。因此，研究如何控制连续刚构桥跨中长期过度下挠具有十分重要的现实意义。

1 工程概况

某三跨双肢薄壁连续刚构桥跨径组合为64 m+115 m+64 m，为直腹板单箱单室预应力混凝土箱梁，采用纵向和竖向两向预应力，左右两幅，双向两车道。桥面宽度为11.0 m+2×0.5 m，荷载标准为汽车-20级，挂车-100。预应力混凝土箱梁顶板宽12.0 m，底板宽6.0 m；梁高在边跨梁端及中跨跨中均为2.5 m，在墩顶根部为6.0 m，其余主梁梁高变化采用二次抛物线变化。腹板厚度采用0.4、0.5 m，仅在主梁0号块为0.7 m。主墩及箱梁均采用C50混凝土，承台采用C30混凝土，桩基采用C25混凝土。桥型布置如图1所示。

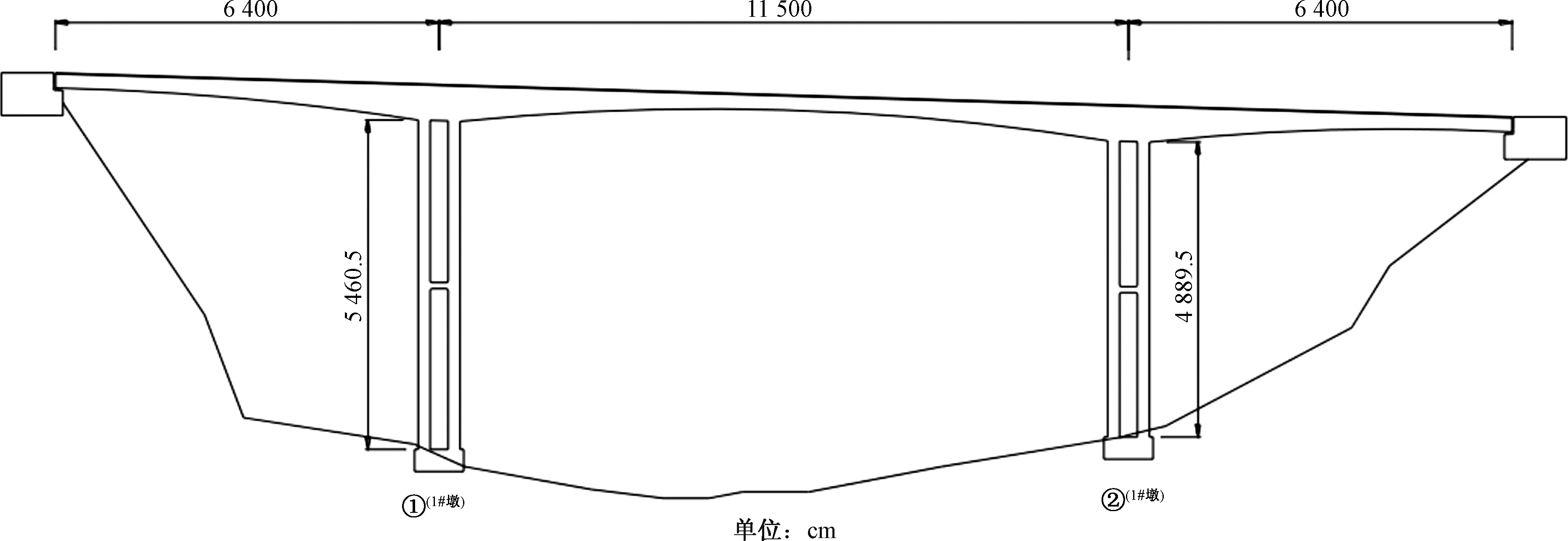
图1 桥型布置

该桥2004年4月完成合拢，于2006年11月竣工，因其病害自建成至2010年持续增加，中跨跨中下挠值持续增大，自建成起6年间桥梁中跨跨中累计下挠137 mm，故2011年7月相关单位对该桥进行了体外预应力加固处治，加固工程于2011年8月通过竣工验收。但根据后续几年的检测报告，该桥中跨跨中仍继续下挠，并且其趋势未得到有效抑制，至2017年2月，该桥中跨跨中已累计下挠204.9 mm。

2 原桥有限元模型建立

本文采用杆系模型[1]建立该桥的全桥有限元模型，模型中共建立节点277个，单元224个，预应力钢束(仅考虑纵向预应力)142根，采用两端张拉方式。其中主梁离散为93个节点，92个单元；单个承台、基础及桩基共离散为74个节点，66个单元。采用一般支承在主梁的两端模拟边界，以此约束Y方向和Z方向的线位移；采用刚性的弹性连接在双肢薄壁墩与主梁固结处进行连接，桥墩与桩基的连接、桥墩系梁与墩的连接均采用刚性连接，桩基底部全约束。在模型中，施工阶段的设置根据图纸设定的施工步骤进行，并设置其分析类型为线性累加模型。桥梁有限元模型如图2所示，2011年加固处治后新增体外预应力束布置如图3所示。

结合所建立的该桥全桥有限元模型及历年下挠情况，以混凝土徐变变形、底板钢束径向力和预应力损失为主要影响因素[2]，分别分析三者对连续刚构桥跨中下挠的影响。

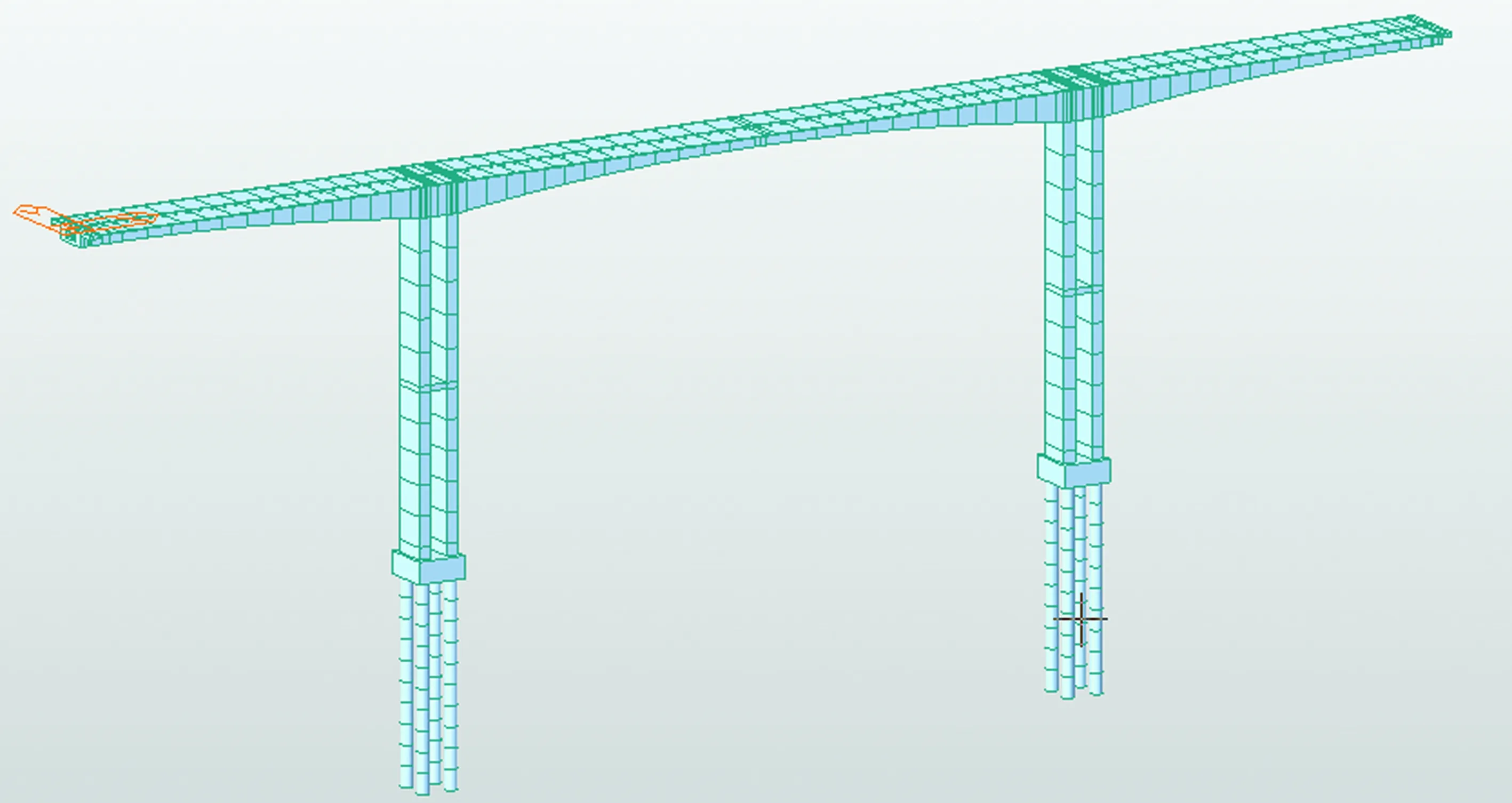
图2 全桥有限元模型

图3 2011年新增体外预应力束布置图

3 下挠原因分析

3.1 混凝土徐变对挠度的影响分析

混凝土收缩徐变会引起结构应力重分布[3-4]，对于连续刚构桥这种多次超静定结构而言影响更为突出，将引起附加内力和徐变次内力，且会导致预应力损失，致使结构挠度不断增大，对桥梁线形产生重大影响。对混凝土徐变变形的主要影响因素包括加载龄期、环境湿度和温度效应等，该桥已建成投入运营，其长期挠度主要受施工时混凝土的加载龄期及后期时间效应的影响。本节主要研究该桥施工时加载龄期对其跨中下挠的影响[5]。

加载龄期会影响混凝土的成熟度，加载龄期短，混凝土水化反应仍在进行，其强度尚未达到设计值，混凝土成熟度差，加重了混凝土最终的徐变变形。该桥在施工过程中存在赶工现象，预应力筋张拉时混凝土龄期普遍较短，多数箱梁梁段在混凝土浇筑后仅3 d即进行了预应力筋张拉。

本文所研究的连续刚构桥始建于2002年，故徐变的计算采用标准《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ 023—85)附录4中的规定，徐变系数：

φ(t,τ)=βa(τ)+0.4βd(t-τ)+φf[βf(t)-βf(τ)]

(1)

(2)

式中：φ(t,τ)为加载龄期为τ、计算龄期为t时的混凝土徐变系数；βd(t-τ)为滞后弹性应变，大小随时间增长；βf(t)、βf(τ)为滞后塑性应变，大小随混凝土龄期而增长；R(τ)/R(∞)为混凝土龄期为τ时的强度与最终强度之比；φf为流塑系数，φf=φf1φf2，φf1为依周围环境而定的系数，φf2为依理论厚度h而定的系数；h=2λAh/μ，λ依周围环境而定，Ah为构件混凝土截面面积，μ为与大气接触的截面周边长度。

考虑到加载龄期对徐变系数的影响，取混凝土初次加载龄期为3、5、7、10 d 4种计算模型，分别研究其对主梁挠度的影响。以构件理论厚度1 m为例，采用图纸设计的环境相对湿度70%，加载龄期为3、5、7、10 d的混凝土徐变系数φ(t,τ)如图4所示。

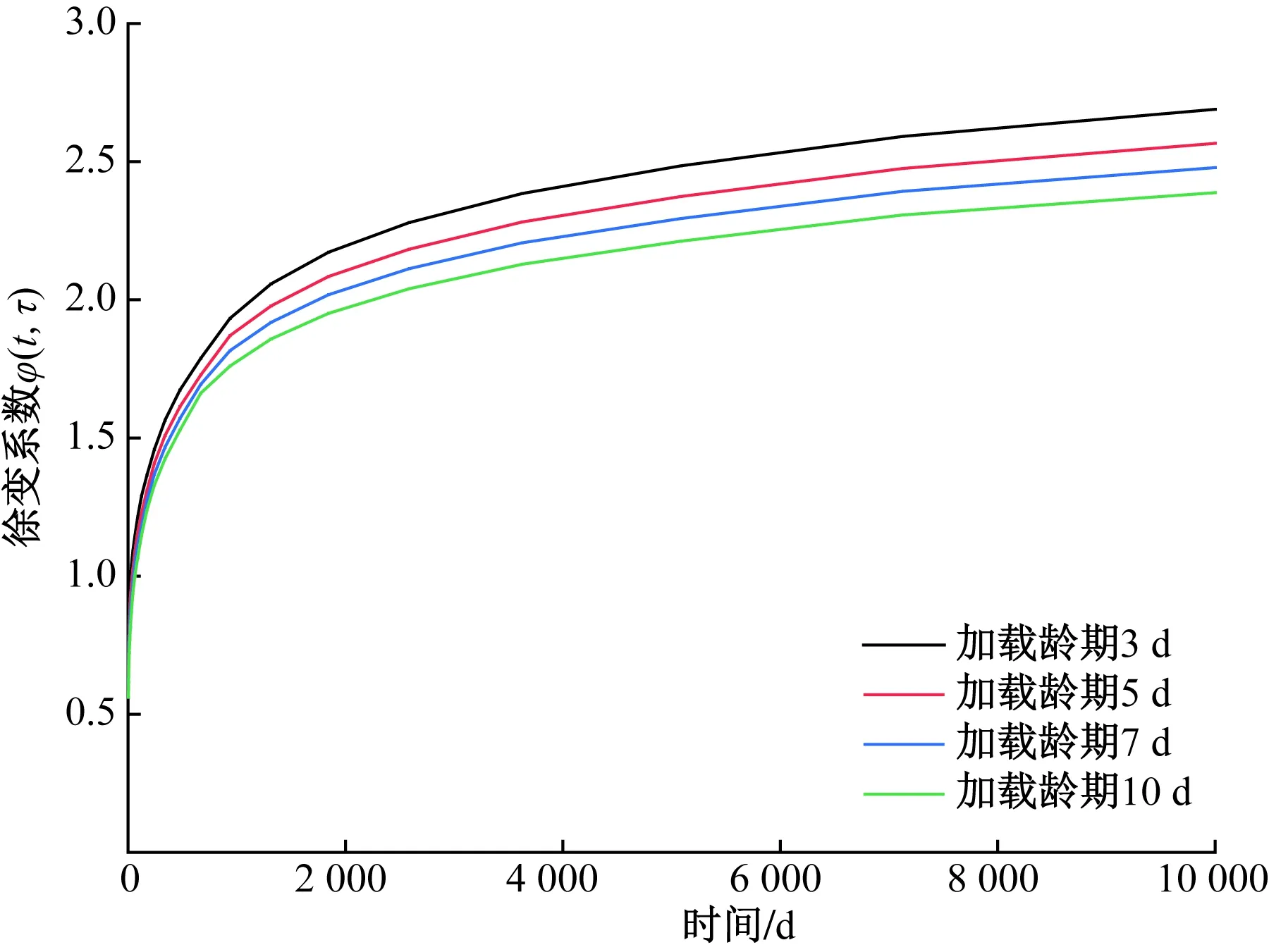
图4 不同加载龄期的混凝土徐变系数

由于该桥在2011年加固处治时进行过体外预应力加固，故在研究不同加载龄期对主梁下挠的影响时按以下3种情况分别进行考虑。

1)自成桥至2017年10月以考虑体外预应力加固为条件，主梁混凝土初始加载龄期为3 d时相比于初始加载龄期为5、7、10 d时的下挠量变化。

2)自成桥至2017年10月以不考虑体外预应力加固为条件，主梁混凝土初始加载龄期为3 d时相比于初始加载龄期为5、7、10 d时的下挠量变化。

3)自成桥至2017年，分别考虑主梁是否增加体外预应力在混凝土初始加载龄期为3、5、7、10 d时的下挠量变化。

3种情况所对应的图像如图5～图7所示。

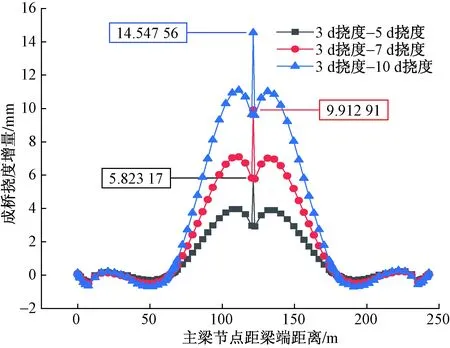
图5 考虑体外预应力加固情况下初始加载龄期3 d相比于5、7、10 d主梁成桥挠度增量

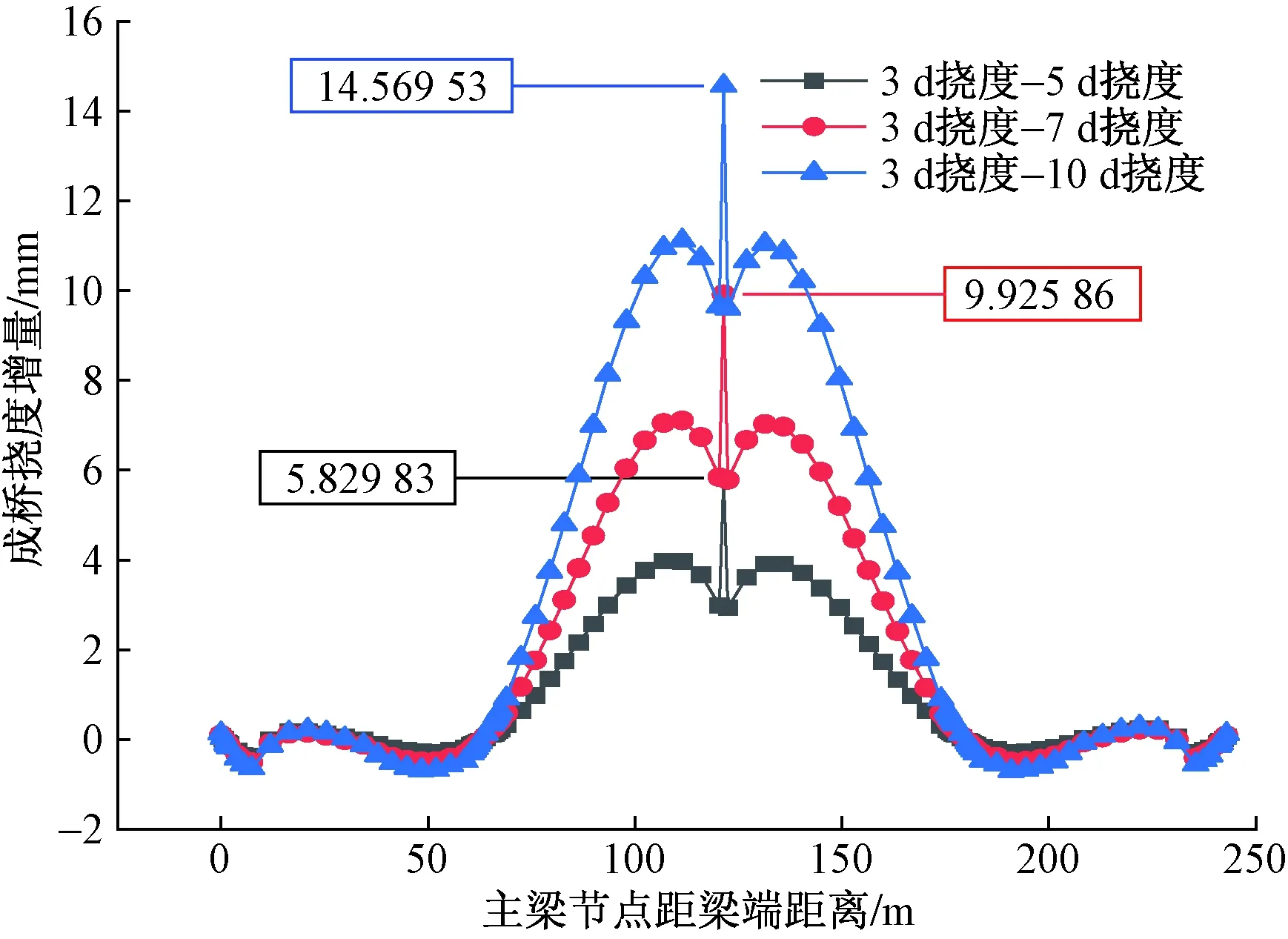
图6 不考虑体外预应力加固情况下初始加载龄期3 d相比于5、7、10 d主梁成桥挠度增量

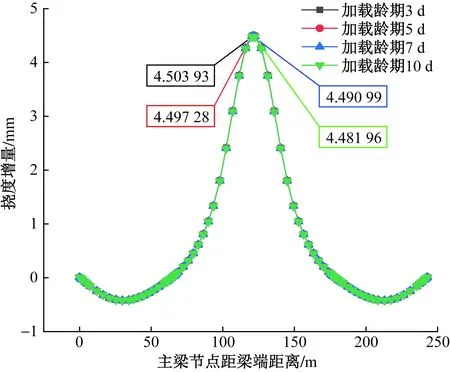
图7 不同加载龄期是否考虑体外预应力主梁挠度增量

由图5～图7分析可得，主梁节段混凝土初始加载龄期越短，成桥挠度就越大。在未考虑体外预应力加固的情况下，主梁初始加载龄期为3 d时相比于初始加载龄期为5、7、10 d时，跨中最大下挠量增加率分别达到4.51%、7.93%、12.09%；在考虑体外预应力加固的情况下，主梁初始加载龄期为3 d时相比于初始加载龄期为5、7、10 d时，跨中最大下挠量增加率分别达到4.37%、7.67%和11.68%。主梁混凝土初始加载龄期为3、5、7、10 d时，未增加体外预应力相比于增加体外预应力的跨中最大下挠量增加率分别达到3.34%、3.49%、3.59%、3.73%。可见，考虑体外预应力加固后，主梁下挠情况有些许改善，但仍未有效抑制下挠趋势。

3.2 底板钢束径向力对挠度的影响分析

钢束径向力实质为在大跨度预应力连续刚构桥中跨合拢进行预应力筋张拉时，由于悬臂施工及结构受力的需要，桥梁梁高设置一般呈现为圆曲线渐变或抛物线形态，而为了实现拉直状态，受到张拉力而绷紧的钢束将挤压预应力管道壁，从而对周围混凝土产生的附加荷载效应。图8为两端锚固点处存在部分微小弯起时的钢束径向力分布示意。预应力钢束在传统连续刚构桥中的布置及其径向力计算图示如图9所示。

图8 钢束径向力分布

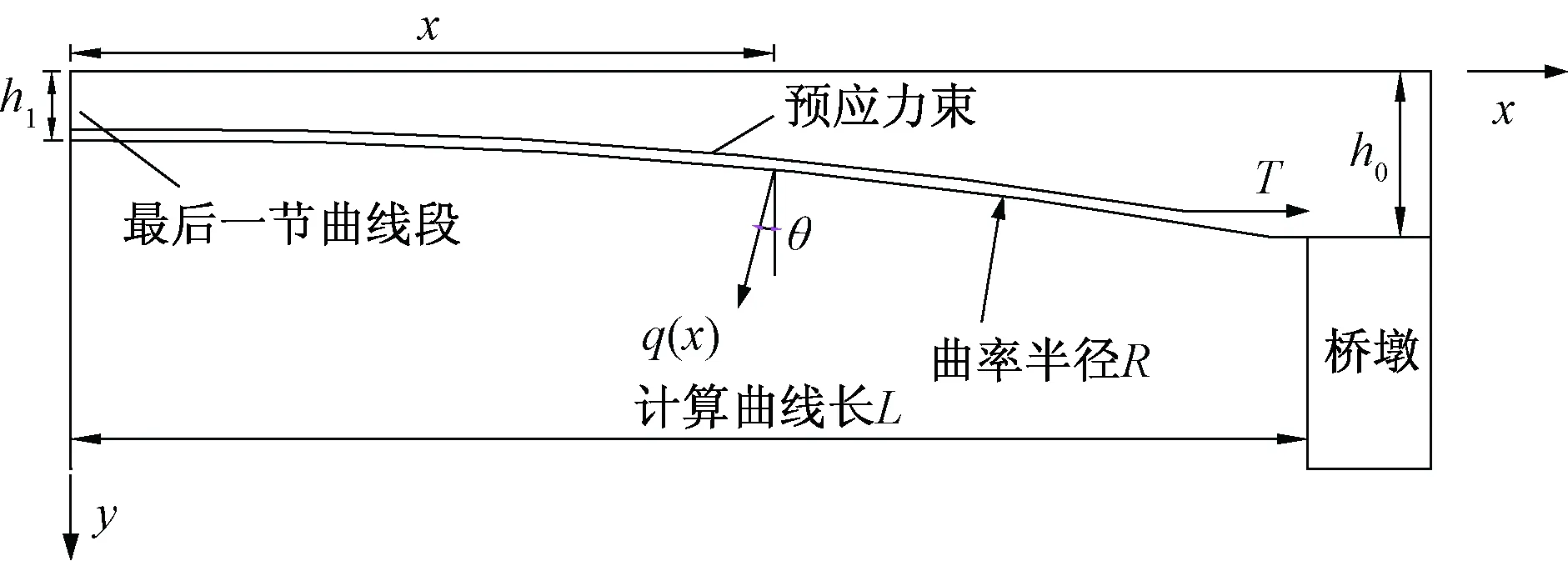
图9 预应力钢束布置及计算图示

由图9可知，θ为梁底面的切线与x轴的夹角，θ=arctan(y′)；T为预应力钢束张拉时的拉力，dx为钢束上的任意微段；q(x)为径向力集度[6]。连续刚构桥底板预应力钢束布置的曲线方程为

(3)

式中，k为连续刚构桥底面抛物线次幂。

根据力的平衡方程，当底板预应力钢束按照式(3)的曲线方程进行布置时，有

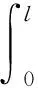
(4)

由于当x=0时，θ=0，由牛顿-莱布尼茨公式得

q(x)dx=-Tdθ=-Td[arctan(y′)]

(5)

(6)

式中：负号是由于在预应力钢束张拉时，其所接触的梁体混凝土为预应力管道壁上侧，故由于力的相互作用，钢束径向力q(x)作用方向向下。

对式(3)求导得式(6)中的一阶导数和二阶导数：

(7)

(8)

为研究底板钢束径向力对该桥跨中下挠的影响，根据吴国松[7]、陈海波等[8]提出的水平底板索技术，将钢束径向力简化计算后反向加载至该桥有限元模型，将水平底板钢束消除径向力后以原曲线钢束加反向加载的径向力来取代，并且忽略两端锚固点处钢束的部分微小弯起。钢束沿底板曲线布置，整体上凸。根据牛顿第三定律，钢束锚固力与张拉力在不考虑损失的情况下，二者数值相等，方向相反，则有

T张拉=T锚固

(9)

由图9可知，底板钢束在其两锚固点之间将沿底板曲线呈现向上凸的形状，在其张拉时，钢束锚固力所产生的轴向力会在竖向和水平方向分解出竖向和水平分力，其中水平分力因钢束对称布置将相互抵消。竖向分力为

T竖=T锚固sinθ

(10)

式中，θ为钢束上一点与水平方向的夹角，竖向分力T方向竖直向上，竖向合力为2T，又因合力在竖直方向上数值为0，即

∑y=0

(11)

故此时底板预应力钢束将受到与其相接触的预应力管道上侧混凝土对其向下的力的作用，此作用将使钢束产生方向向下的均布荷载q，即径向力。此径向力将竖向合力2T抵消，故其数值为

(12)

式中，l为钢束布置长度。

根据本文所研究连续刚构桥的收集资料，全桥均采用弹性模量为1.95×105MPa的φj15.2-16规格低松弛270钢绞线组成纵向预应力钢束。根据竣工图纸，单根钢束张拉力为313.6 t，钢束张拉力T张拉=313.6×9.8=3 076.22 kN。根据该桥设计说明及立面图得，梁高于墩顶根部为6.0 m，边跨梁端及中跨跨中均为2.5 m，其余主梁采用二次抛物线形梁高变化，计算曲线长L=53 m。则可得底板预应力钢束布置的曲线方程及其一阶导数：

(13)

(14)

结合式(14)及θ=arctan(y′)，先求得钢束锚固点切线与x轴的夹角，进而求得钢束锚固力的竖向分力，最终求得简化的钢束径向力。计算结果列于表1。

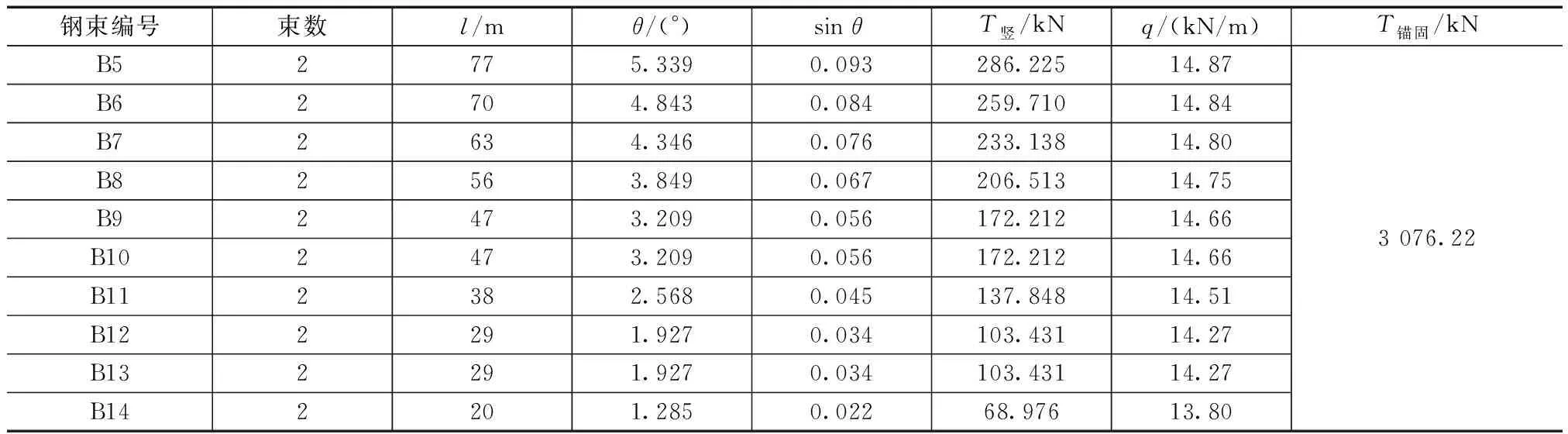
表1 底板钢束简化径向力数值

为近似模拟消除底板钢束径向力工况，将求得的简化径向力反向加载到该桥的有限元模型中，具体数值如图10所示；该桥自成桥至2017年10月未消除钢束径向力与消除钢束径向力所导致的成桥挠度如图11、图12所示；消除钢束径向力相比于未消除钢束径向力所引起的挠度减少量如图13所示。

图10 底板反向径向力分布

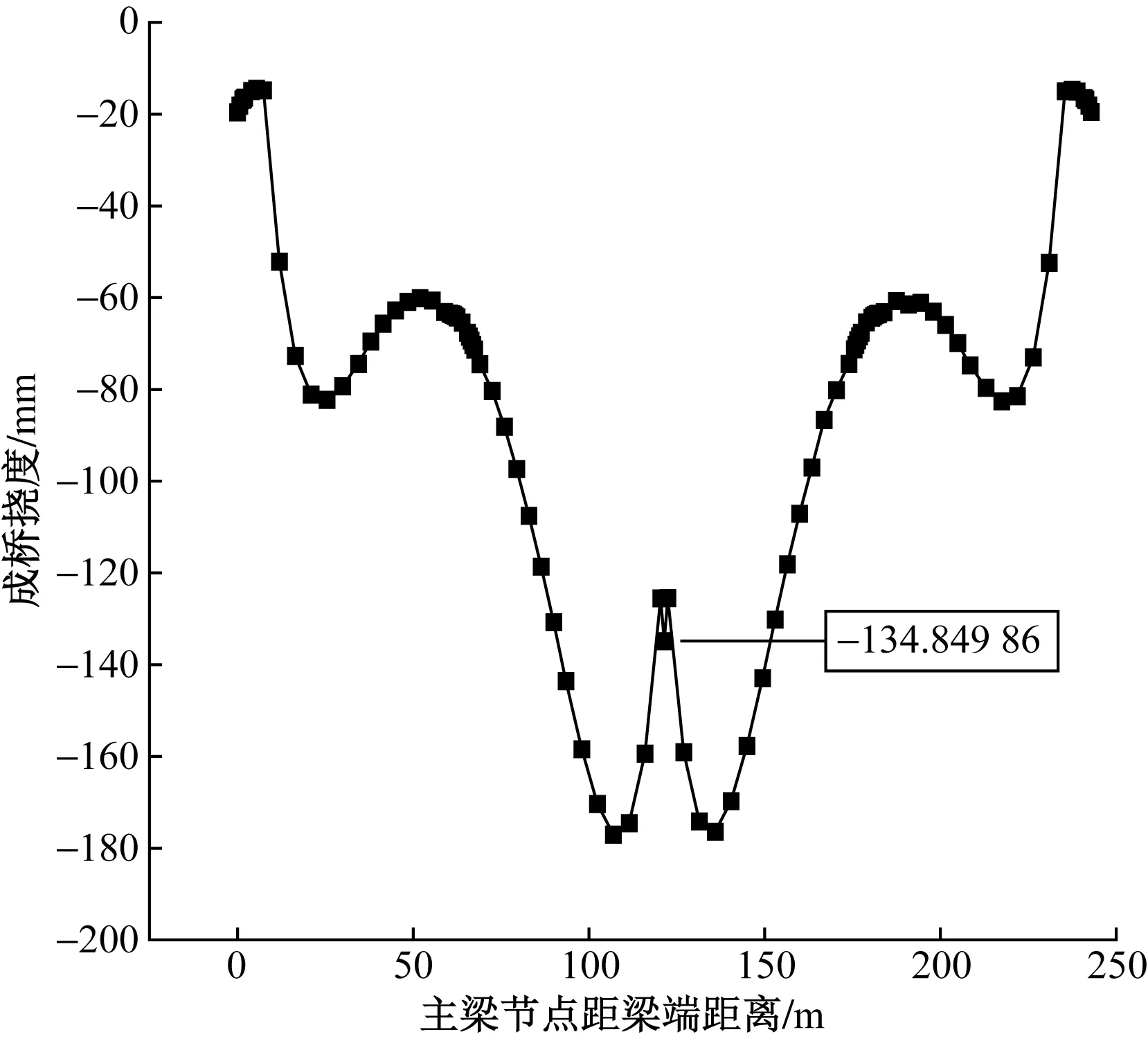
图11 未消除径向力主梁成桥挠度

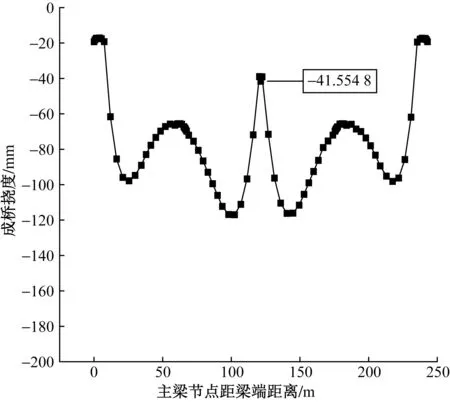
图12 消除径向力主梁成桥挠度

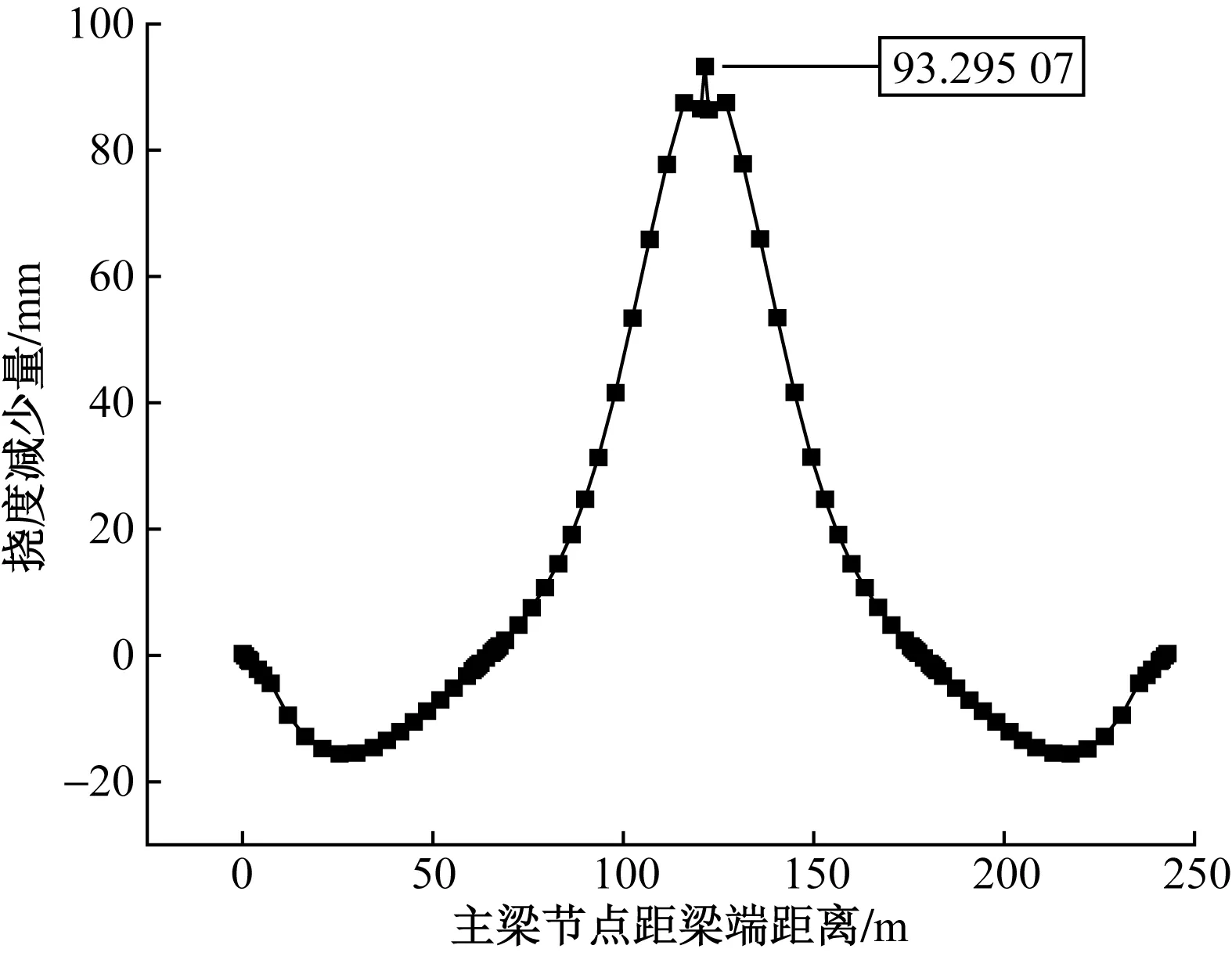
图13 消除径向力相比于未消除径向力所引起的挠度减少量

据图11～图13分析可知，底板钢束径向力对本文所研究连续刚构桥的中跨跨中下挠影响十分明显。其中当消除径向力时与未消除径向力时中跨跨中最大下挠量分别为41.55 mm和134.85 mm。消除钢束径向力相比于未消除钢束径向力最大下挠率减少了69.18%。

3.3 钢束预应力损失对挠度的影响分析

在预应力混凝土连续刚构桥进行预应力设计时，纵向预应力设计是其核心问题[9-11]，纵向预应力钢束在主梁各截面上提供预压应力，以使各个截面有足够的抵抗弯矩的强度。在实际工程中，受施工质量、所处环境等因素的影响，桥梁预应力筋的预拉应力将逐渐减少，即结构预应力损失，其中纵向预应力的损失对预应力混凝土连续刚构桥跨中下挠的影响最为明显。

在原图纸预应力设计值、加载龄期3 d的基础上，分别在纵向预应力折减为10%、20%、30%时分析预应力损失对该桥中跨跨中下挠的影响，并且按照3种情况进行考虑。

1)该桥自成桥至2017年10月以考虑体外预应力为条件，纵向预应力折减分别为10%、20%、30%时相比于无纵向预应力折减的成桥挠度变化。

2)该桥自成桥至2017年10月以不考虑体外预应力为条件，纵向预应力折减分别为10%、20%、30%时相比于无纵向预应力折减的成桥挠度变化。

3)该桥自成桥至2017年，纵向预应力折减分别为10%、20%、30%时，是否考虑体外预应力的成桥挠度变化。

3种情况所对应图像如图14～图16所示。

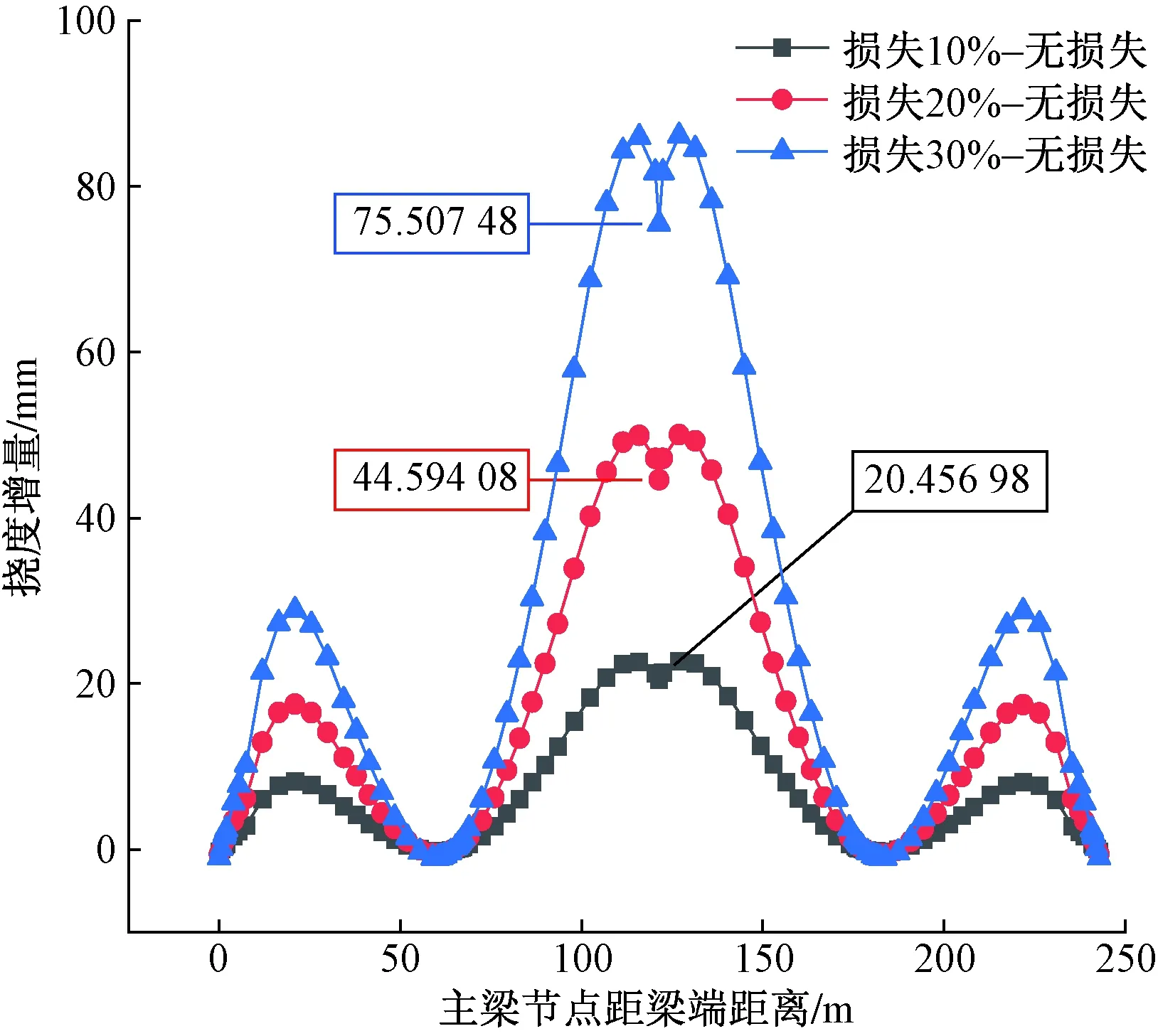
图14 考虑体外预应力条件下纵向预应力损失为10%、20%、30%时，相比于无预应力损失的挠度增量

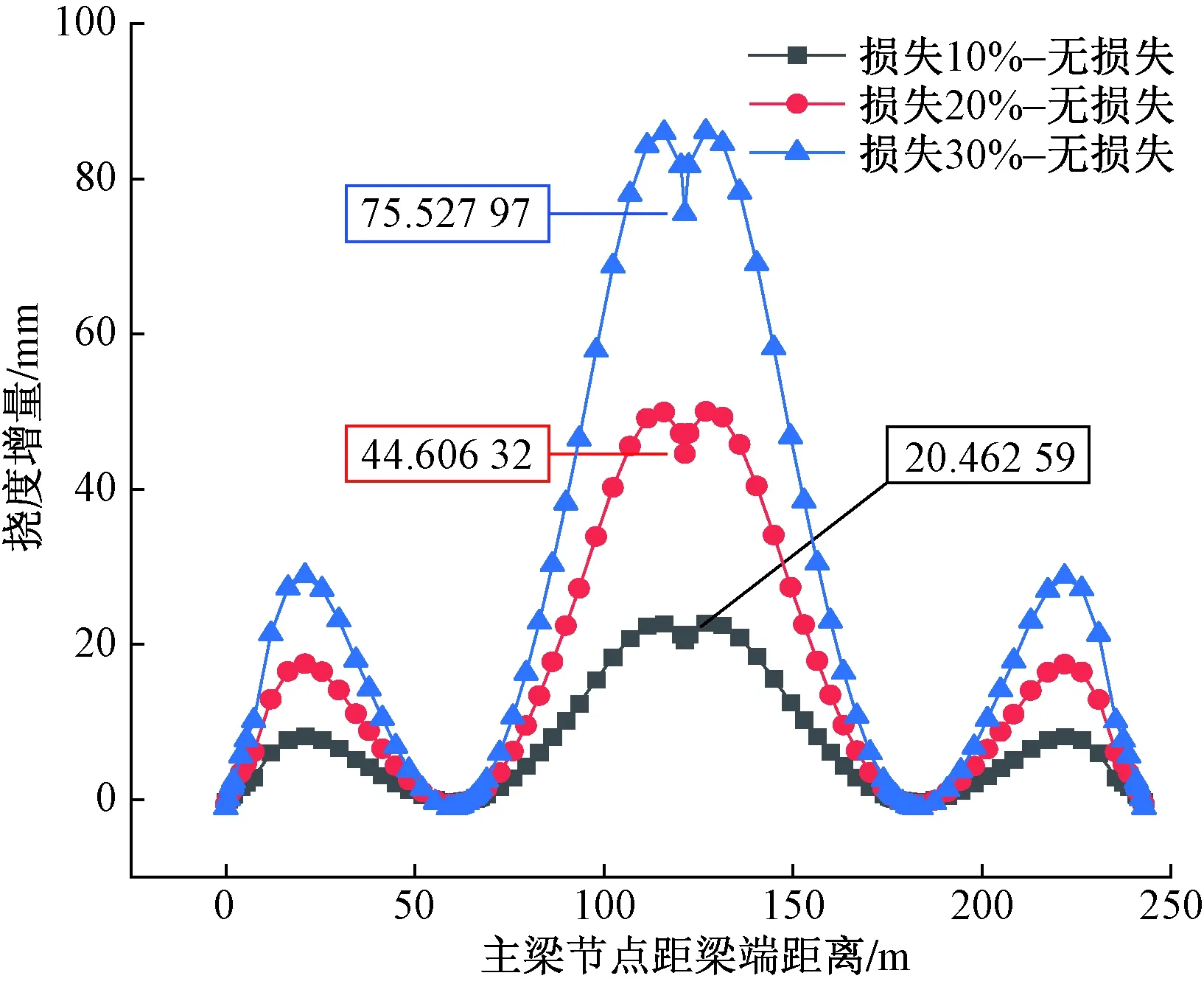
图15 不考虑体外预应力条件下纵向预应力损失为10%、20%、30%时，相比于无预应力损失挠度增量

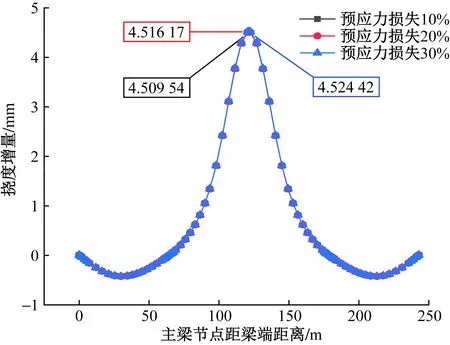
图16 纵向预应力损失为10%、20%、30%时，是否考虑体外预应力的成桥挠度增量

由图14～图16分析可知，主梁节段钢束纵向预应力损失越多，成桥挠度越大。在不考虑体外预应力的情况下，纵向预应力折减分别为10%、20%、30%时相比于无纵向预应力折减，跨中最大下挠量增加率分别达到15.17%、33.07%和56%；在考虑体外预应力的情况下，纵向预应力折减分别为10%、20%、30%时相比于无纵向预应力折减，跨中最大下挠量增加率分别达到14.68%、32.01%和54.2%。纵向预应力折减分别为10%、20%、30%时，不考虑体外预应力相比于考虑体外预应力的跨中最大下挠量增加率分别为2.9%、2.52%和2.15%。考虑体外预应力加固后，主梁下挠情况有些许改善，但仍未有效抑制下挠趋势。

4 结论

1)在该桥多数箱梁梁段在混凝土浇筑后仅3 d即进行了预应力筋张拉的情况下，若不考虑预应力损失，根据模型结果比较，在混凝土加载龄期为3 d时，主梁的成桥挠度最大，即由于该桥主梁节段初始加载龄期过短，致使徐变变形过大。但模型分析所得挠度结果仍未接近实际检测结果，其原因既有程序计算和桥梁有限元模型计算所选择参数等引起误差，也包括因桥梁施工质量等因素引起的严重病害。在当下施工技术日趋先进的条件下仍不应当为追求施工速度而在施工过程中盲目缩短混凝土加载龄期。

2)底板钢束径向力对连续刚构桥中跨跨中下挠的影响十分明显，消除径向力对于控制预应力混凝土连续刚构桥跨中下挠有显著效果。在未来桥梁建设中可以考虑将水平底板索替代曲线索，从而改善预应力混凝土连续刚构桥的下挠问题。

3)纵向钢束预应力损失对连续刚构桥主梁跨中下挠的影响非常突出。当纵向预应力损失达到30%时，跨中最大下挠增加率可达50%以上，这导致本文所研究连续刚构桥结构刚度降低，引起跨中下挠问题加剧。