多龄期锈蚀钢结构框架柱力学性能研究

王 婷，王明飞

(1.成都职业技术学院，四川 成都 610041; 2.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

0 引 言

钢结构的性能（如承载力、刚度和延性等）会受到环境因素的影响，其中最为明显的是腐蚀环境下对钢结构的性能影响。对于既有钢结构建筑，随着其在酸性大气环境下服役时间的增加，将导致其锈蚀程度增大，进而使得结构承重试件截面削弱及钢材强度和延性的降低，引起结构性能发生变化，如在水平地震作用下的层间位移增大，结构安全将受到严重威胁。基于材料层面，钢材腐蚀后其强度和延性下降，腐蚀生成的物质不能提供强度，导致构件有效截面减损，不均匀腐蚀形成腐蚀坑，引起应力集中[1-2]。

对既有钢结构在未来可能发生的地震作用下发生各种不同程度的破坏进行评估显得尤为重要，且目前国内外基于结构耐久性的抗震性能研究较少，主要集中于材料方面，主要以试验研究为主。史炜洲等[3]对锈蚀钢材的力学性能进行了实验研究，得到了受腐蚀钢材的屈服强度，抗拉强度和伸长率随着腐蚀程度的增加而下降的结论。郑山锁等[4]对处于酸性大气环境下的钢材力学性能进行了一系列的试验，研究表明钢材力学性能随着龄期的变大而变差，如钢材的屈服强度，抗拉强度，伸长率和弹性模量等均随着龄期的增大而减小。文献[5]通过对我国不同地区和不同龄期的工业钢结构建筑进行了耐久性能实测与材料性能试验，提出了钢材的腐蚀模型及力学性能退化模型。曹楚南等[6]对钢材在多种环境下的腐蚀行为进行了一系列研究，积累了大量的试验数据。范颖芳等[7-15]对锈蚀钢材进行了试验研究，研究表明钢材的力学性能指标与失重率基本呈线性关系。从构件或者结构角度，史炜洲[3]对锈蚀钢梁的力学性能进行了研究，得到了锈蚀钢梁的承载力和刚度均随着锈蚀的增大而减小。王晓飞等[16-17]建立了时变概率地震需求模型、时变概率抗震能力模型及时变易损性模型，并分析了结构易损性随服役年限的衰减规律。

近年来，在考虑环境因素（腐蚀）下，锈蚀对钢材材料，构件和结构的性能影响研究方面已积攒了大量的研究，但对于锈蚀对钢结构柱构件的承载力和性能研究较少，也缺乏从纤维模型角度去模拟锈蚀钢结构构件性能的研究。因此，本文主要通过建立锈蚀钢材力学性能的损伤退化规律，从纤维模型角度，基于Opensees对锈蚀钢结构柱的性能进行了初步研究，为我国的多龄期钢结构地震性能提供了基础。

1 锈蚀钢材力学性能模型

为研究多龄期锈蚀钢结构构件和结构性能的退化规律，首先需研究锈蚀对钢材力学性能的影响，因此需要建立锈蚀钢结构力学性能模型。

钢材锈蚀会引起其截面的削弱及力学性能的改变，为定量描述钢材试件的锈蚀程度，本文采用失重率D来描述钢材的锈蚀程度，D为钢材锈蚀前的质量减去钢材锈蚀并除锈后的质量与钢材原质量的比值，D越大就表示该试件的锈蚀程度越严重，失重率D的计算公式如下：

其中W和W'分别为钢材锈蚀龄期分别为0年和t年试件的质量，单位为g，其中t为结构的锈蚀龄期，单位为年。例如钢构件截面采用H型钢，失重率D可表达成以下形式：

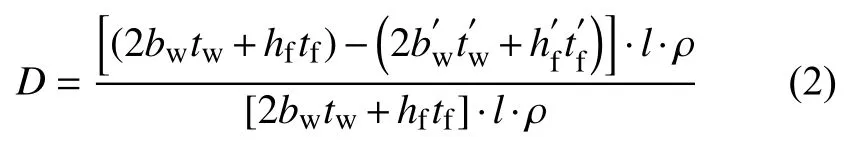
式中：l——H型钢构件的长度；

ρ——钢材的密度；

bw和b′w——结构锈蚀龄期分别为0年和t年时试件翼缘宽度；

tw和t′w——结构锈蚀龄期分别为0年和t年时试件翼缘厚度；

hf和h′f——结构锈蚀龄期分别为0年和t年时试件腹板高度；

tf和t′f——结构锈蚀龄期分别为0年和t年时试件腹板厚度。

其中b′w=bw-2Kt，t′w=tw-2Kt，h′f=hf-2Kt，t′f=tf-2Kt，K为钢材腐蚀速率。

为建立锈蚀钢材的力学性能退化模型，需收集钢材在腐蚀环境下的力学性能试验，建立锈蚀钢筋力学性能数据库，收集的锈蚀钢材力学性能试验需符合以下准则：

1）钢材的材料等级为Q235B，为大部分钢结构常用的材料，具有代表性。

2）钢材的含碳量在0.08%左右。

3）钢材所处环境为国际标准化组织ISO 12944—2腐蚀环境中的C3环境，即本文钢材腐蚀率K为30 μm/a。

从文献中收集的锈蚀钢材力学性能试验数据和拟合结果如图1所示。从图中可看到锈蚀钢材的屈服强度、抗拉强度和伸长率均随着钢材失重率的增大而减小。

图1 锈蚀钢材力学性能与失重率的关系

锈蚀钢材的力学性能指标拟合公式为：

式中：fy和f′y——多龄期锈蚀前后钢材的屈服强度；

fu和fu′——多龄期锈蚀前后钢材的极限强度；

δ和δ′——多龄期锈蚀前后钢材的伸长率。

而多龄期锈蚀钢材的弹性模量退化规律采用文献[4]中提及的退化规律，如下式所示：

其中E和E′分别为多龄期锈蚀前后钢材的弹性模量。

2 多龄期钢结构Opensees数值建模

2.1 锈蚀H型钢柱pushover数值模拟

为研究多龄期锈蚀钢结构构件的性能，以H型钢柱为例进行说明，柱截面尺寸为300 mm×200 mm×6 mm×8 mm，高度为3 000 mm，钢材采用Q235钢材。为了对不同锈蚀龄期(锈蚀龄期t为0年、15年、30年、45年)的 H型钢柱进行 pushover分析，建模过程中需要定义各龄期结构钢材的力学性能。通过锈蚀后钢材材性试验，得到锈蚀后钢材的力学性能随着失重率变化的退化规律见式(3)、式 (4)、式 (5)和式 (6)。在建模过程中，多龄期Opensees有限元模型中的材料非线性采用Steel01模型，在Opensees材料属性输入中采用式(3)、式(4)、式(5)和式(6)计算得到的各龄期结构的钢材力学性能指标。截面采用纤维截面模型，构件采用基于位移法的非线性梁柱单元，并考虑P-Delta效应。图2为Opensees有限元模型示意图，可看到，模型分为6个节点，5个梁柱单元，从Node 1～Node 5中，每个节点之间的距离为500 mm，而Node 5～Node 6之间的距离为1 000 mm。

图2 Opensees有限元模型示意图

图3为多龄期锈蚀H型钢柱在不同龄期(锈蚀龄期t为0年、15年、30年、45年)下的荷载-位移曲线，可看到随着锈蚀龄期t的增大，荷载-位移曲线的屈服点和峰值点逐渐增大，表明多龄期锈蚀H型钢柱的承载力随着锈蚀龄期的增大而下降，刚度随着锈蚀龄期的增大而降低。从图3中，还可看到在荷载-位移曲线具有明显的屈服点和最高点，表明采用文中的Opensees有限元模型可较好地模拟了锈蚀多龄期H型钢柱的水平荷载-位移曲线前半段。而在锈蚀H型钢柱达到最大承载力后曲线较为快速下降。原因是文中的Opensees有限元模型中所采用的Steel01材料模型中对钢材的极限拉应变进行截断，即钢柱在实际受力过程中，当钢材应变达到或大于极限拉应变时，钢材的所承担的应力值为零。因此，计算模拟的水平荷载-位移曲线在峰值点承载力后出现下降段。从图3中可进一步看到，其曲线后半段结果一开始下降而后又逐渐上升，这是由于软件的数值计算问题引起的钢柱承载力达到最低点后再继续增长，表明多龄期锈蚀H型钢柱的水平荷载-位移曲线后半段增长的结果较为失真。由图3可看到，多龄期(锈蚀龄期t为0年、15年、30年和45年)锈蚀H型钢柱的四条水平荷载-位移曲线下降段的趋势较为一致，表明多龄期锈蚀对钢柱的后期承载力的变化趋势影响较小。

图3 多龄期锈蚀H型钢柱荷载位移曲线

2.2 锈蚀H型钢柱低周期反复试验模拟

为了研究多龄期锈蚀钢结构构件的地震性能，将以H型钢在低周期反复为例进行说明，柱截面尺寸同样为 300 mm ×200 mm ×6 mm ×8 mm，其有限元模型均与2.1节相同。基于Opensees有限元平台，模拟了不同锈蚀多龄期(锈蚀龄期t为0年、15年、30年、45年)的锈蚀H型钢柱低周期反复荷载试验。图4所示为不同锈蚀多龄期(锈蚀龄期t为0年、15年、30年、45年)的H型钢柱低周期反复荷载位移曲线。从图4可看到随着锈蚀龄期t的增大，H型钢柱的承载力、位移和延性逐渐下降，表明多龄期锈蚀H型钢柱的承载力、位移和延性均随着锈蚀龄期t的增大而降低。从图4中可看到，随着锈蚀龄期t的增大，多龄期锈蚀H型钢柱的软化特征逐渐增大。从图4的4个多龄期锈蚀H型钢柱的水平荷载-位移滞回曲线对比中可进一步看到，随着锈蚀龄期t的增大，多龄期锈蚀H型钢柱的滞回环逐渐缩小，表明多龄期锈蚀H型钢柱的耗能能力随着锈蚀龄期t的增大而降低。从图4中可知，随着锈蚀龄期t的增大，多龄期锈蚀H型钢柱的滞回环基本保持棱形形状，基本呈现出一种弯曲破坏为主的破坏模式，由此表明多龄期锈蚀H型钢柱的破坏模式基本不随锈蚀龄期t的增大而改变。

图4 多龄期锈蚀H型钢柱反复荷载位移曲线

2.3 不同截面形式对多龄期钢结构构件性能影响

通过2.2节的多龄期锈蚀H型钢柱作为特殊实例，已经验证Opensees有限元建模计算的有效性，在本节中，进一步将其再推广到其他型钢柱构件。因此，为了研究不同截面形式对多龄期锈蚀钢结构构件性能的影响，基于Opensees有限元计算分析软件，本文进行了不同截面形式下，在经历了不同锈蚀龄期(锈蚀龄期t为0年、15年、30年、45年)下锈蚀钢结构柱的数值模拟研究，结合式(3)、式(4)、式(5)和式(6)得到不同锈蚀龄期t下钢结构构件的钢材力学性能。本文采用的钢结构柱子截面形式分别为H型钢柱，不对称H型钢柱，工字钢柱，槽钢柱和方钢柱，如表1所示，采用的Opensees有限元模型建模方法与2.1节相同。表中H型钢柱截面为截面高度×宽度×腹板厚度×翼缘厚度； 不对称H型钢柱截面为截面高度×上翼缘板宽度×下翼缘板宽度×腹板厚度×上翼缘板厚度×下翼缘板厚度；工字钢表示方法与H型钢相同； 槽钢柱截面尺寸为腰部高度×腿部宽度×腰部厚度×腿部厚度；方钢管柱截面尺寸为截面宽度×截面高度×厚度。

表1 多龄期锈蚀钢结构框架柱不同截面尺寸

图5中的数据点为各种截面形式下钢柱力学性能退化指标与失重率之间的关系，可看到无论是哪种截面形式，锈蚀钢柱的承载力和位移均随着失重率的增大而下降，可得锈蚀钢结构构件的性能随着龄期的增长而下降。从图5可明显看到，相对于其他截面形式而言，方钢管钢柱性能随着龄期的增大，承载力和位移下降比其他截面形式的钢柱小。

2.4 多龄期钢结构构件性能退化模型

为了研究多龄期钢结构构件性能退化的一般规律，通过采用最小二乘法，对2.3节中各种截面形式下多龄期锈蚀钢柱的承载力与位移性能拟合分析，可得多龄期钢结构构件性能退化模型，如图5所示。多龄期钢结构构件性能退化模型如下式所示：

式中：P和P'——多龄期锈蚀钢结构框架柱锈蚀前后的峰值承载力；

Δ和Δ'——多龄期锈蚀钢结构框架柱锈蚀前后的峰值承载力对应的位移。

从（7）和式（8）可看到多龄期钢结构构件性能退化模型与失重率是呈负线性关系，即多龄期钢结构构件性能随着失重率的增大而下降。本文所提出的多龄期钢结构构件性能退化模型需要进一步的试验研究进行验证，也为多龄期钢结构整体结构性能研究提供了基础。

3 结束语

本文通过研究典型酸性大气环境下钢材的性能退化规律，进而提出锈蚀钢材材料退化模型，采用Opensees有限元计算分析软件平台，对各种截面形式下的多龄期锈蚀钢结构框架柱进行了数值模拟，提出了模拟多龄期锈蚀钢结构框架柱的有限元数值模型，基于本文的研究，可得以下结论：

1）多龄期锈蚀钢材的力学性能指标，如屈服强度，抗拉强度和伸长率等，均随着龄期的增大而下降，基本呈线性关系。

2）多龄期锈蚀钢柱的承载力和刚度性能指标均随着龄期的增大而下降，也基本呈线性关系。

3）截面形式对多龄期锈蚀钢柱性能变化有一定的影响，相对于其他截面形式而言，方钢管钢柱性能随着龄期的增大，承载力和位移下降比其他截面形式的钢柱小，表明这种截面形式可以有效的防止龄期对钢构件性能的影响。