基于IGOA-RBF的矿用风压传感器温度补偿研究

吴新忠，耿 柯，陈 昌

(中国矿业大学信息与控制工程学院，江苏 徐州 221008)

0 引 言

矿井智能通风的精准调控依赖于控制系统前端通风参数的精准监测。在矿内温、湿度和灾害气体等通风参数测量已经能满足精度要求的前提下，风压参数的快速准确测量成为关键，风压参数测量精度高，风网解算与智能调控将更精准[1]。当前，硅压阻式风压传感器因其体积小、灵敏度高、响应速度快等综合优势成为煤矿通风系统风压参数的主流采集设备。由于矿井环境温度的干扰[2]，导致测得的风压参数精度降低，需要对风压传感器进行温度补偿。

风压传感器的温度补偿主要有硬件和软件两种方式。由于硬件补偿存在电路温漂、价格昂贵和普适性不高的缺点[3]，学者们针对风压传感器的温度漂移软件补偿进行了大量研究，具体地有插值法、曲面拟合法[4]和人工神经网络方法等。其中，人工神经网络因其强大的非线性映射能力被广泛应用。文献[5]对应变片式压力传感器的温度漂移问题，建立快速非排序遗传算法(non-dominated sorting genetic algorithm,NSGA-Ⅱ)优化的误差反向传播(back propagation,BP)神经网络温度补偿模型，提高了应变片式压力传感器的测量准确度。文献[6]通过建立粒子群算法(particle swarm optimization,PSO)优化的BP神经网络温度补偿模型，改善了压力传感器的温漂现象。与BP神经网络相比，径向基神经网络(radial basis function,RBF)训练过程中需要调节的结点和权值较少，训练速度更快。文献[7]表明RBF对电化学CO气体传感器的温补精度高于BP的补偿精度。但RBF存在易陷入局部最优解的缺点，蝗虫优化算法(grasshopper optimization algorithm,GOA)是一种新的智能优化算法，具有全局优化、收敛速度快等优点，目前被应用于多目标优化、作业车间调度、参数优化等方面[8-9]。

本文针对硅压阻式风压传感器存在的温度漂移问题，提出了一种基于改进蝗虫算法优化的径向基神经网络(IGOA-RBF)温度补偿方法。通过佳点集均匀初始化蝗虫种群和自适应非线性参数变化两种策略改进GOA算法，利用改进的蝗虫算法优化的RBF神经网络对风压传感器进行温度补偿，减小了温度对风压传感器造成的影响。

1 压阻式风压传感器温度漂移特性

压阻式风压传感器利用硅的压阻效应，通过半导体工艺在硅片上扩散4个电阻构成惠斯通电桥，通过惠斯通电桥将风压转换为电信号，再通过小信号放大电路、模数转换电路等过程，最终转化为实际待测风压。风压传感器的桥臂电阻R和灵敏度K是关于温度的函数：

式中：RN——常温下的电阻值；

α——温度系数；

ΔT——温度变化值；

μ——半导体的泊松系数；

πL——压阻系数；

E——弹性模型；

A、β——掺杂系数；

T——温度。

传感器的灵敏度K和压阻系数πL有关，而πL又是关于温度T的函数，T越高，πL值越小，灵敏度K则越低[10]。当工作环境温度变化时，风压传感器输出会发生温度漂移。温度漂移具体包括零点漂移和灵敏度漂移。

通过对风压传感器在不同温度下的输入输出特性曲线进行测量，得到传感器的温度漂移特性如图1所示。在给定相同的压力下，当温度为25 ℃时，风压传感器的输入输出特性曲线是一条理想的特性曲线，即输出压力值等于给定标准压力值；当温度高于25 ℃时，随着温度升高，传感器输出值向比标准值偏大方向变化；当温度低于25 ℃时，随着温度降低，传感器的输出值向低于标准值方向漂移。从图中可以看出：1）风压传感器在零点处存在严重漂移，当温度为-20 ℃时，风压传感器的输出值漂移至-0.132 kPa；在温度60 ℃时，给定压力0 kPa，传感器的输出值漂移至0.080 4 kPa。2）不同温度下的传感器输入输出特性曲线并不平行，表明风压传感器的灵敏度发生漂移。

图1 风压传感器温度漂移特性

风压传感器灵敏度和温度的关系如图2所示，可以看出，温度由-20 ℃升到60 ℃，传感器的灵敏度从1.15 K降至0.9 K。因此风压传感器的温漂导致传感器的精度降低，需要采取一定的补偿方法来提高传感器的精度。

图2 风压传感器灵敏度和温度的关系

2 GOA-RBF风压传感器补偿算法

2.1 RBF神经网络温度补偿模型

图3 风压传感器的RBF温度补偿模型

Cj、bj、wj分别是第j个结点的数据中心、扩展常数和输出权值。本文RBF神经网络参数的调整是通过最小化均方误差函数：

式中：N——训练数据的个数；

ei——误差信号；

Yi——第i个训练数据的期望值。

2.2 蝗虫优化算法

蝗虫优化算法模拟蝗虫在自然界中的种群迁徙和觅食行为[11]，将蝗虫的幼虫和成年期，对应于算法中的局部开发和全局搜索。将蝗虫位置映射为解，蝗虫个体向食物源移动的过程，对应于搜索个体的最优解选取过程。

蝗虫位置的更新主要依靠蝗虫个体当前位置、全局最优位置以及其他蝗虫个体共同决定，所有蝗虫个体都会参与其他蝗虫个体位置的更新：

式中：xi——第i个寻优个体的位置；

dij——第i个体与第j个个体之间的相对空间距离；

(ub)d和(ld)d是第d维的上下界，c是平衡勘探与开发的参数，随迭代次数的增加有利于减小蝗虫在目标值附近的距离。计算如下：

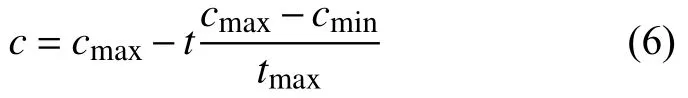
式中：t——当前迭代次数；

tmax——最大迭代次数；

cmax、cmin——参数的上下限值。

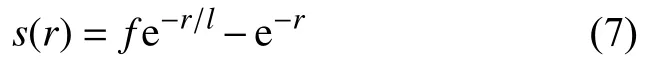
2.2.1 均匀随机初始化种群

GOA算法初始蝗虫种群个体的均匀性和多样性，可以提高算法的搜索速度和寻优质量。而随机初始化蝗虫种群则无法保证蝗虫个体分布的均匀性[12]。

用佳点集取点的方式点的分布均匀性要好于随机取点，并且理论证明佳点集取点的偏差要远小于随机取点的偏差[13]。

在GOA算法要优化的d维单位立方体Gd中，要求佳点rk满足：

p是满足上式的最小质数，然后构造佳点集PN(i)：

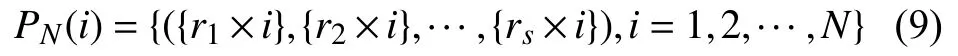
2.2.2 非线性自适应参数

GOA中的参数c在算法前期影响全局优化性能，在算法后期决定着局部开发能力，线性递减的变化方式，将导致前期下降速率较快，无法进行全局探勘，后期下降速度较慢，不易跳出局部最优[14]。为平衡算法在不同迭代时期的全局探索和局部开发能力，采用非线性变化的自适应曲线，即：

采用非线性递减参数，前期c较大且下降速率较慢，这样有助于算法在充足的时间内在全局范围内寻优，后期 c较小且变化快，可使算法快速收敛。

2.3 IGOA-RBF温度补偿算法

径向基函数的Cj、bj以及wj的随机初始化，会导致网络的收敛方向具有不确定性，易陷入局部最优，无法保证神经网络的精度。GOA具有全局优化、可调参数少等优点。改进后GOA初始种群更加均匀，算法收敛速度更快，利用IGOA优化算法对RBF参数进行寻优，将最佳的bj、Cj、wj参数组合赋值给RBF神经网络对风压传感器进行温度补偿。IGOA-RBF温度补偿算法具体步骤如下：

1）设置种群规模N、进化代数tmax。将bj、Cj、wj作为每个GOA个体的一组维度信息。利用佳点集进行种群均匀初始化。

2）导入风压传感器实测数据并将其进行归一化操作，将网络输出的均方误差作为蝗虫位置更新的适应度函数，用式(4)作为计算初始种群的个体适应度。

4）用式(10)更新参数c。

5）根据位置更新公式(5)和适应度更新最新目标值。

6）利用IGOA寻优得到的RBF神经网络最优初始参数，导入样本集，训练RBF神经网络温度补偿模型。

7）导入测试集进行模型验证。

3 实验结果分析

3.1 实验数据的获取

实验系统如图4所示，实验器材：美国Druck的PACE5000高精度压力控制器、高低温试验箱、温度传感器SHT35、风压传感器、相同量程的国外差压传感器以及SIEMENS的S7-1200模块等。标定温度区间是-20～60 ℃，风压传感器量程范围是0～0.5 kPa，国外差压传感器(包括罗斯蒙特、横河EJA和霍尼韦尔)起到温漂参照作用。其中压力控制器的精度为0.001%FS，高低温试验箱的温度范围是-25～140 ℃，准确度是 0.1 ℃，S7-1200 用来采集风压传感器输出数据。

图4 实验系统

将风压传感器和温度传感器放入高低温试验箱，温控箱以10 ℃步长调节温度变化，每个温度点保温2 h之后，再进行加压实验，压力控制器以0.05 kPa压力步长改变压力作为风压传感器的输入，通过PLC进行数据自动采集。实验采集到的原始数据在表1中列出。

表1 风压传感器样本数据

采用如下零点漂移系数公式和灵敏度漂移系数公式来计算温度对风压传感器的影响，补偿前的计算结果在表2中列出。

表2 风压传感器温漂系数 10-3 kPa/(FS·℃)

式中：α0——零点漂移系数；

αs——灵敏度漂移系数；

Tc——当前温度；

TN——常温；

Pt0——当前温度下的零点输出；

PN0——常温下差压传感器的零点输出；

PN——传感器满量程的输出值；

Pt——当前温度下的满量程输出。

3.2 温度补偿

为了使得样本数据更好地覆盖温度、压力区间，首先对样本数据根据预先设置的比例划分为训练和测试两类。为了加快神经网络的学习速度，需要将不同量纲的数据统一到同一量纲下，即需要对样本数据进行归一化处理。如图5所示是归一化后的样本数据。

图5 样本数据归一化

为了比较IGOA算法的优点，选用PSO、GA和GOA算法作对比。其中，粒子群算法按照文献[6]进行参数设置，惯性权重为1，学习因子c1=c2=1.44，遗传算法的参数按照文献[15]设置，交叉概率为0.75，变异概率为0.01，GOA参数和IGOA参数设置相同。各算法的适应度曲线如图6所示。

图6 各优化算法适应度曲线

GA算法在20代左右陷入了局部最小值，PSO算法在150次迭代后接近全局最优，GOA算法在100次迭代后可达到全局最优解，IGOA在50次左右即可收敛到最优解，这是因为采用佳点集均匀初始化蝗虫种群，使得初始种群具有多样性，能够遍布整个搜索区间，并且非线性自适应参数变化能够加快算法后期收敛速度，防止陷入某个局部区域。结果表明IGOA能够快速的找到使误差函数值最小的数据中心、径向基基宽参数和输出权值。

为了验证IGOA-RBF温度补偿模型的性能，分别对传统的RBF、遗传算法优化的径向基神经网络(GA-RBF)、粒子群算法优化的径向基神经网络(PSO-RBF)和蝗虫算法优化的径向基神经网络(GOA-RBF)用同样的测试集对各算法进行测试验证。将算法补偿后的压力值与标准值相对比，以满量程相对误差、均方误差(MSE)、平均绝对误差(MAE)进行评价。各补偿模型上得到的满量程相对误差如图7所示，用RBF神经网络温度补偿后的风压传感器输出相对误差在-0.9%～1.7%之间，用GA-RBF网络补偿后的相对误差在-0.6%～1.3%之间，PSO-RBF网络温度补偿后相对误差为-1.0%～0.9%之间，GOA-RBF网络温度补偿后的相对误差在-0.7%～0.7%区间范围内，IGOA-RBF补偿后相对误差为-0.3%～0.3%之间，经IGOA-RBF补偿后的最大相对误差比经RBF补偿后的降低了1.4%。

图7 不同训练算法的相对误差

如表3所示，IGOA-RBF补偿后的均方误差为6.61×10-7，平均绝对误差为 0.76×10-3kPa，从图 7和表3可以看出相较于RBF、GA-RBF、PSO-RBF和GOA-RBF神经网络，IGOA-RBF神经网络温度补偿模型的补偿精度最高。

表3 各算法性能

IGOA-RBF补偿后的温度漂移系数见表4，对比表2，平均零点温度漂移系数由补偿前的5×10-3kPa/(FS·℃)降为补偿后的2.56×10-4kPa/(FS·℃)，平均灵敏度漂移系数由补偿前的3.08×10-3kPa/(FS·℃)降为补偿后的2.65×10-4kPa/(FS·℃)，经IGOA-RBF补偿后的零点温度漂移系数和灵敏度漂移系数分别降低了94.9%和91.4%。

表4 IGOA-RBF补偿后温漂系数 10-4 kPa/(FS·℃)

IGOA-RBF神经网络在测试集上的补偿输出与期望输出对比如图8所示。测试样本网络输出与给定标准压力基本一致，表明IGOA-RBF温度补偿模型泛化能力较强，补偿精度较高。

图8 IGOA-RBF网络输出与期望值的对比图

经IGOA-RBF神经网络补偿后的全部样本拟合如图9所示。经过IGOA-RBF温度补偿之后，不同温度下的风压传感器输入输出特性曲线基本重合，风压传感器的零点漂移和灵敏度漂移均得到改善。

图9 IGOA-RBF温度补偿后的I/O特性曲线

4 结束语

针对矿用风压传感器因温度漂移导致的风压测量精度降低问题，建立GOA优化的RBF神经网络温度补偿模型，克服了RBF易陷入局部最优的缺陷。利用佳点集均匀初始化蝗虫种群和非线性自适应参数策略改进GOA算法，提高了GOA收敛速度。经IGOA-RBF补偿后的零点温度漂移系数降低了94.9%，灵敏度漂移系数降低了91.4%。IGOA-RBF补偿效果优于GA-RBF、PSO-RBF和GOA-RBF温度补偿模型，IGOA-RBF补偿后的最大相对误差相较于RBF补偿后的降低了1.4%，能有效的消除环境温度变化给风压传感器带来的误差，提高测量精度。