不同风攻角下分离式双箱梁涡振气动力演化和局域相关性研究
李玲瑶,张敬怡,贺诗昌,3,何旭辉,徐汉勇
(1.中南大学 土木工程学院,湖南 长沙,410075;2.高速铁路建造技术国家工程研究中心,湖南 长沙,410075;3.佛山市顺德区乐从桂圃房地产开发有限公司,广东 佛山,528315;4.长沙学院 土木工程学院,湖南 长沙,410022)
为了提高桥梁的颤振抗风性能,大跨度桥梁主梁设计越来越多地采用双幅桥面或分离式双箱梁断面[1-3]。我国西堠门大桥(主跨径为1 650 m)、上海长江大桥(主跨径为730 m)、昂船洲大桥(主跨径为1 018 m),韩国Gwang-yang 大桥(主跨径为1 545 m)均采用这种断面形式。然而,这种分离式双箱梁的空气动力性能研究还处于探索阶段。已有研究发现,设置中央开槽的流线型箱梁的两箱之间存在不可忽略的气动相互干扰作用,相比闭口单箱梁,分离式双箱梁的旋涡脱落模式更明显,且在某些开槽间距和风攻角下的涡振性能可能会更差,发生涡振的概率更高[4-8]。在大量分体式双箱梁的风洞试验和现场实测中均发现了涡激共振现象,例如,在昂船洲大桥的高低雷诺数试验中发现该桥分体箱梁存在涡振现象[9];西堠门大桥分体箱梁加劲梁的不同雷诺数风洞试验中[10]和现场实测中[11]均观测到了不同振幅的涡激振动现象。
近年来,关于分离式双箱梁的涡激振动性能和机理的研究越来越多,大多采用测压、测力及测振风洞试验方法进行研究。KIMURA 等[12]通过节段模型试验,发现分离式双箱梁的涡振特性与箱梁分离的间距密切相关,即使双箱梁的净间距与单箱梁宽之比达到8,双箱梁之间的干扰效应仍不可忽略。刘小兵等[7,13]进一步深入分析了间距这一重要因素对涡振性能的影响,发现上游、下游箱梁在不同间距下存在相互干扰效应。CHEN等[14]对分离式双箱梁进行了实验研究,发现大间隙下双箱梁桥下游箱体上会产生比较大的脉动压力系数,且主梁双箱之间的横梁会导致下游箱体的脉动压力系数增大。LAIMA 等[15-16]研究了雷诺数对分离式双箱梁涡激振动性能的影响,结果表明雷诺数越大,旋涡脱落频率越大,涡激振动幅值也增大。另外,针对分离式双箱梁的涡振控制措施,学者们也进行了进一步研究。李玲瑶等[17]以青岛海湾大桥大沽河航道桥主梁为研究对象,深入研究了导流板特征尺寸(高度、长度和倾角)对分离式双箱梁断面制振效果的影响。YANG等[18-19]通过对6 种开槽率的大跨度分体箱梁涡振性能和4 种涡振控制措施(增加阻尼比及设置导流板、格栅和风障)的抑振效果展开了研究,并给出了指导性意见。综上可见,对于分离式双箱梁涡振的研究多集中在箱梁间距、雷诺数等参数及不同涡振抑制措施对涡振振幅和涡振风速区间的影响,从微观层面揭示分离式双箱梁涡振机理的研究相对较少。
学者们采用风洞测压试验和流场显示相结合的方式深入研究了槽宽变化和桥面附属结构对分离式双箱梁在静止时的绕流特性、表面风压分布和振动时的涡振性能的影响,发现槽宽变化、桥面附属结构均会改变箱梁周围的流态模式,并伴有涡振类型的变换[20-21],即涡振过程中气动力具有明显的演化特性。刘圣源等[22]利用风洞测压测振试验,对中央开槽箱梁断面扭转涡振过程中不同阶段的表面气动力的发展变化规律及其对涡振效应的贡献率进行了研究,并将其与流线型闭口箱梁的相应结果进行了比较,在一定程度上量化了涡振发生过程中的气动力致振机理。
在通常情况下,实际桥梁结构的来流攻角范围一般为±3°,但复杂风场环境下的分离式双箱梁易遭受-3°~3°范围之外的大攻角来流风,此时,主梁涡振性能与常规攻角情况下的差异较大。因此,本文通过节段模型同步测振测压风洞试验,针对1座大跨度斜拉桥,研究在不同常规攻角和大攻角来流情况下分离式双箱梁表面不同局部特征区域涡振过程中风压分布统计特性及气动力演化特性的变化规律,并分析其与整体气动力的相关性。
1 风洞试验
1.1 模型与试验概况
以某斜拉桥的分离式双箱主梁断面为研究对象,成桥状态主梁主要振型和自振频率如表1所示。风洞试验在中南大学风洞实验室高速段中进行,高速试验段宽为3 m、高为3 m、长为15 m,风速可控范围为1~94 m/s,湍流度小于0.5%。主梁节段模型几何缩尺比为1:60,相应的特征高度H为66.6 mm,特征宽度为857.5 mm,长度为1 810 mm(长宽比为2.1∶1),双箱梁的净间距D与单箱梁宽度B之比为0.48。模型整体刚度由铝合金鱼骨式框架提供,外衣由ABS 板覆面提供,桥面布置有轻轨检修通道和防撞护栏,底板下布置有检修轨道,均选用ABS 板雕刻而成,并粘贴在外衣表面。分离式双箱梁模型示意图如图1所示。
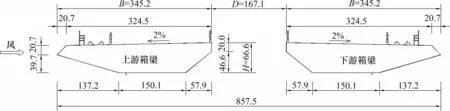
图1 分离式双箱梁模型示意图Fig.1 Sectional model diagram of the separated twin-box girder
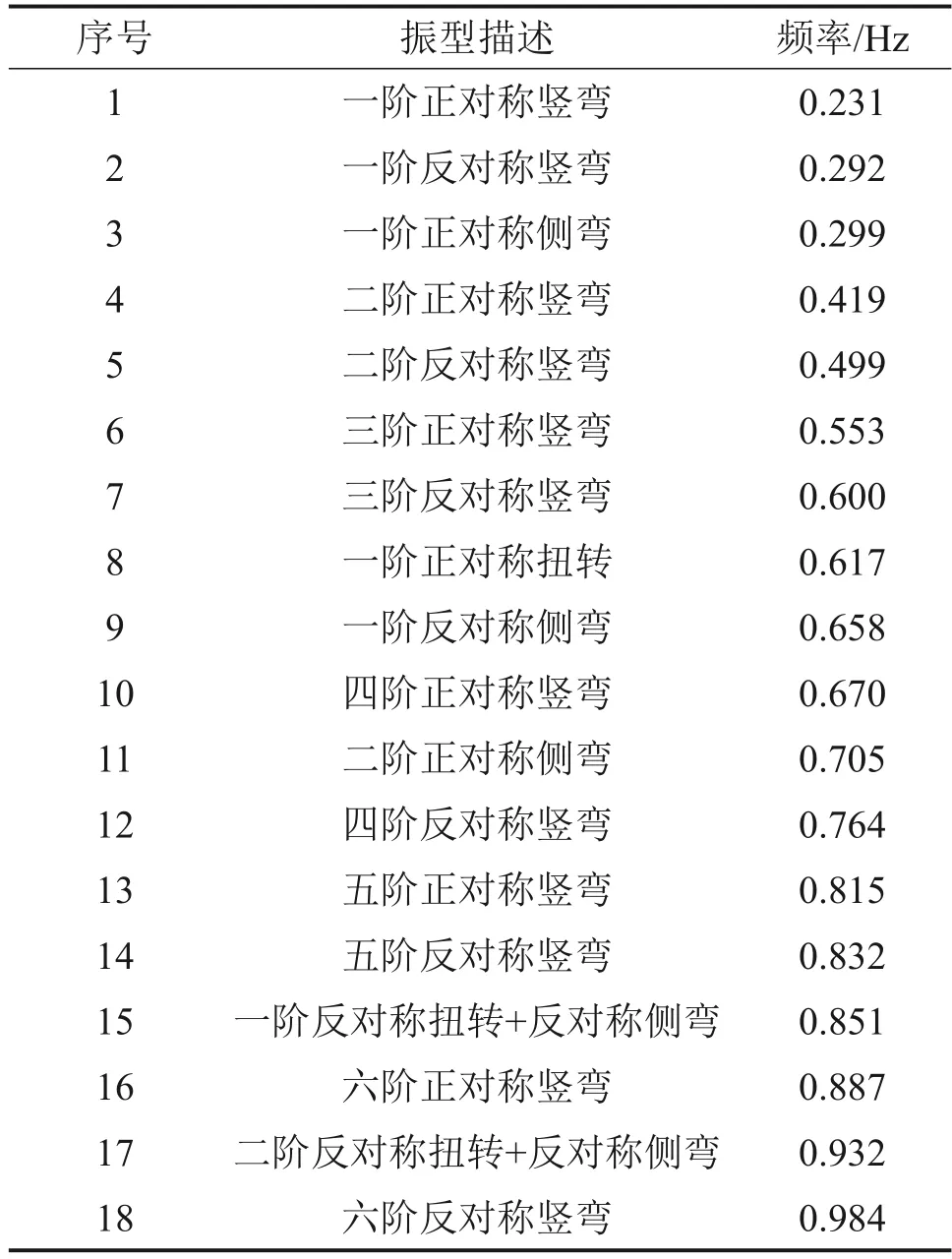
表1 成桥状态主梁主要振型和自振频率Table 1 Main vibration modes and natural frequencies of the girder in completed bridge status
为了获得分离式双箱梁表面风压特性,在模型沿跨向正中无横梁位置处,沿横断面周向布置了一圈测压孔作为测点,考虑到气流绕流在拐角处更为复杂,测压孔布置会适当加密,大多数测点间距为5~20 mm,个别间距为30~35 mm,根据来流方向,将双箱梁分为上、下游2个断面,上游对应测点A-1~A-52,下游对应测点B-1~B-52,两断面测点均对称布置。模型测压点布置如图2所示。
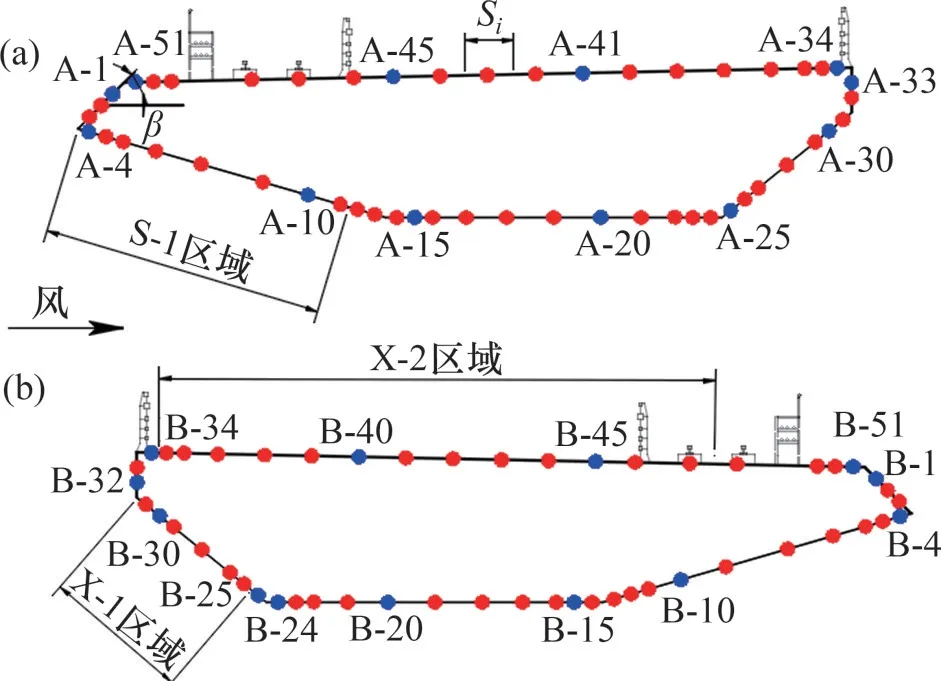
图2 模型测压点布置图Fig.2 Layout of pressure taps in the sectional model
模型两端固接2根刚性吊臂,每根吊臂上下对称设置4根弹簧,并悬挂安装在刚性框架上,从而形成整个弹簧悬挂系统。刚性框架与模型两端之间设置大端板,保证端板与模型端部间隙足够小且在试验中不会发生碰撞,以避免三维绕流效应。4个激光位移计对称布置在吊臂下侧。模型测压孔通过放置在模型内腔的1.5 m长的测压管与设置在刚性框架上的DSM3400 电子式压力扫描阀连接,保证所有测压点均能同步采集,试验采样频率为333.3 Hz,采样时间60 s。节段模型悬挂系统及风洞试验测试仪器布置如图3所示。

图3 同步测振测压节段模型试验条件Fig.3 Synchronous displace and pressure testing conditions of sectional model
模型安装完成后,通过自由振动法对试验模型进行动力特性测试。主梁节段模型主要参数如表2所示。
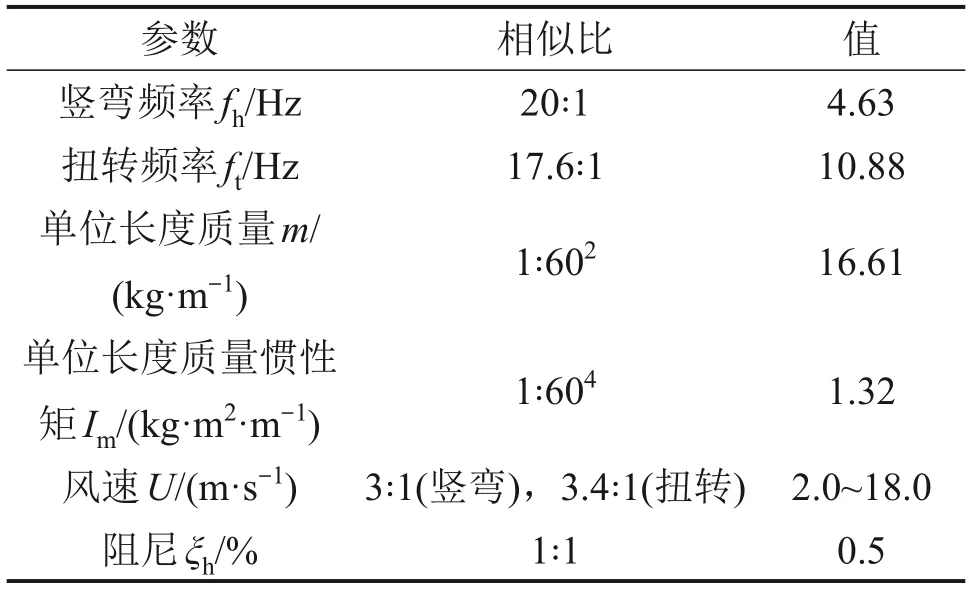
表2 主梁节段模型主要参数Table 2 Main parameters of sectional model of girder
1.2 涡振响应
试验均在均匀流场中进行,来流风速为2.0~18.0 m/s,对应基于主梁特征宽度的雷诺数范围为1.16×105~1.04×106。通过在弹簧线性范围内调节弹簧伸长量来设置风攻角5°,3°,0°,-3°和-5°,数据采集时间均设置为60 s。在所有风攻角下,均出现了竖弯涡振现象,竖弯涡振响应结果如图4所示。需要特别说明的是,本文给出的所有位移(或振幅)均为试验模型的位移(或振幅),风速均为风洞试验风速。由图4可知,在测试风速范围内出现了两个明显的竖弯涡振锁定区间。在第一涡振锁定区间内,竖弯涡振响应随风攻角的增加而递增,而在第二涡振锁定区内,涡振响应随风攻角的变化规律恰巧与第一涡振锁定区间的变化规律相反。
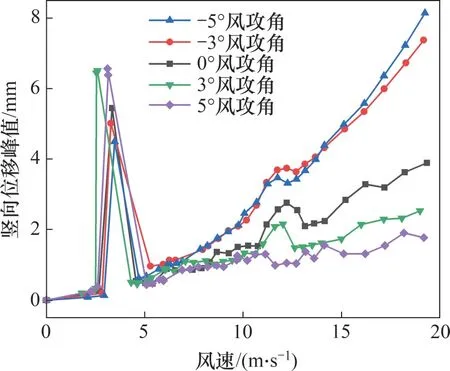
图4 竖弯涡振响应Fig.4 Ⅴertical ⅤIⅤ responses
选取分离式双箱梁模型在风攻角0°时的竖弯涡振响应(见图5),分别对第一涡振锁定区和第二涡振锁定区任一风速时的竖向位移时程进行频谱分析,得到最大竖向位移幅值谱,如图6所示。由图6 可见,2 个涡振锁定区间分别对应2 个不同的卓越频率4.70 Hz 和19.42 Hz,结合表1 可知,其与原型桥梁的一阶正对称竖弯频率0.231 Hz和六阶反对称竖弯频率0.984 Hz 按20:1 换算后的频率接近。虽然第一涡振区间内涡振响应较大,但考虑到低风速时风速不稳定,风速测点太少,仅针对第二涡振锁定区间研究风攻角变化对分离式双箱梁表面分布气动力演变特性的影响。下面分别对风攻角为-5°,-3°,0°,3°和5°下主梁发生最大涡振振幅时表面风压力分布情况进行分析。
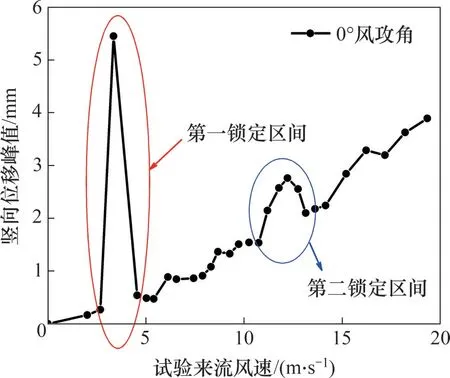
图5 0°风攻角时竖弯涡振响应Fig.5 Ⅴertical ⅤIⅤ responses at wind attack angle of 0°

图6 最大竖向位移幅值谱Fig.6 The maximum vertical displacement magnitude spectrums
2 不同风攻角下分布气动力演变规律
钝体箱梁在来流风下的表面压力不仅能够反映断面气流绕流情况,还可以反映气动力变化的整体过程及变迁过程[23]。根据节段模型表面压力信号,对比和分析不同风攻角下涡振发生时箱梁表面气动力分布特征及演变特性,包括断面各测点时域内的压力系数均值、压力系数根方差及局部特征区域气动力频谱。
2.1 测点压力系数
本文采用测点量纲一压力系数[24]来判断气流在主梁断面的分离及再附情况:
式中:Ci(t)为i测点风压系数时程;pi(t)为i测点处风压时程,压力为正,吸力为负;ρ为空气密度;Ud为相应工况下来流平均风速。分离式双箱梁节段模型拐角、栏杆、检修通道等特殊位置及区域与测点的对应关系见表3。

表3 测点设置Table 3 Pressure taps setting
箱梁表面平均压力系数的分布状况可表征气流在模型表面的总体分布特征,据此能够判断气流在箱梁断面上的分离和再附情况[22]。在不同风攻角下,分离式双箱梁上下游断面发生最大涡振振幅时的测点平均压力系数如图7所示。由图7可以看出:除了上游断面迎风侧上斜腹板和顶板检修通道前缘区域及-3°和-5°风攻角下游断面内外防撞护栏之间受正压作用外,其余部分均受负压作用,平均风压系数在上游断面迎风侧风嘴和轻轨检修轨道附近发生突变,出现很大的负压,说明气流在此处发生强烈的分离作用,在大多数风攻角下,这种旋涡分离会一直延续到下游断面的尾部,但受检修轨道、防撞护栏、断面拐角局部位置干扰,负压强度会产生突变。
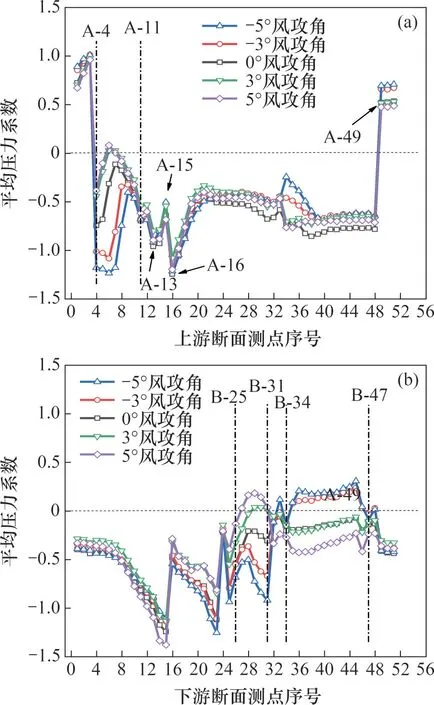
图7 不同风攻角下最大涡振振幅时测点平均压力系数Fig.7 Mean pressure coefficient distribution under different attack angles during maximum ⅤIⅤ amplitudes
对于上游断面,气流经过迎风侧风嘴后,在上游第4 个测点(A-4)处和轻轨检修通道前端发生分离,风压由正变负,除负攻角时迎风侧下斜腹板中间区域外,其他区域测点均为负压,仅在检修轨道、防撞护栏和断面拐角处局部区域出现气压波动,表明未出现明显的再附现象。当风攻角从5°变化到-5°时,迎风侧下斜腹板上的负压呈现阶梯状增强,且受风嘴气流分离作用区域宽度增大;背风侧直腹板与顶板相交附近区域风压随风攻角的变化规律则相反,所承受负压随风攻角减小有显著减小趋势。除此之外,上游断面的其余区域风压随风攻角减小的变化趋势不明显。
对于下游断面,当风攻角从5°变化到-5°时,迎风侧下斜腹板区域平均风压系数发生变化,负压增加显著,且迎风侧直腹板附近区域平均风压系数接近于0,说明在迎风侧下斜腹板与直腹板交界处附近气流发生了分离再附,在底板及背风侧斜腹板区域形成气流分离区,且随风攻角减小,负压强度变化不大;随风攻角减小,内侧防撞护栏到轻轨检修通道之间区域所受压力由负变正,负攻角时正压显著增加,说明随着风攻角由正变负,气流经内侧防撞护栏后在顶板产生的分离作用增强;另外,受到底板与背风侧斜腹板交界处拐角的干扰,气流分离强度会突然增强,断面其他拐角处气流也均有不同程度的突变,但程度不及拐角干扰影响下的大。
气流流经浸没的钝体时,多次流动分离和再附必会产生作用于钝体表面的脉动压力,可通过模型表面压力系数的根方差得知模型表面脉动压力。图8所示为断面在最大涡振振幅时不同风攻角下各测点脉动压力系数。由图8可以看出,在各风攻角下,上游断面各测点脉动压力系数相比于下游断面较小。在上游第33 个测点(A-33)、下游第24 和34 个测点(B-24 和B-34)处脉动压力系数随风攻角的变化非常小,而这些测点附近区域的脉动压力系数会迅速增大甚至达到最大,且随风攻角变化发生显著变化,说明气流在模型开槽处上下拐角处会积蓄能量,脱落旋涡与箱梁开槽处区域发生撞击并产生强烈的耦合作用,从而造成这些测点脉动压力系数变化幅度较大。
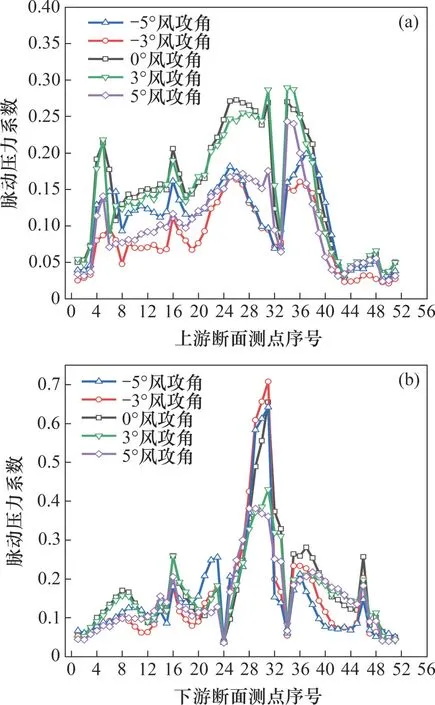
图8 不同风攻角下最大涡振振幅时测点脉动压力系数Fig.8 RMS distribution of fluctuating pressure coefficients under different attack angles during maximumⅤIⅤ amplitudes
对于上游断面,在风攻角为0°和3°时,大部分测点脉动压力系数均比其他风攻角条件下的大;顶板除A-34~A-41测点处的脉动风压系数随风攻角的变化趋势相差显著外,其他区域变化趋势差异不明显;背风侧直腹板、迎风侧斜腹板、背风侧斜腹板及底板各区域范围内测点的脉动压力系数随风攻角的变化趋势基本一致,除拐角外,各板脉动风压系数对0°和3°风攻角不敏感,背风侧直腹板和斜腹板对负风攻角变化亦不敏感;另外,在背风侧直腹板临近的测点脉动压力系数随风攻角的变化相较于其他拐角附近测点的变化更显著。
对于下游断面,在风攻角为0°和3°时,除B-24~B-34测点外,大部分区域的脉动压力系数均比其他风攻角条件下的大;B-24~B-34测点之间迎风侧直腹板和斜腹板表面脉动压力系数在正风攻角和负风攻角时的差别相较于其他区域显著,且此区域脉动压力系数达到最大;而在5°风攻角下,脉动压力系数在断面不同区域变化明显,背风侧斜腹板区域和迎风侧直腹板区域的脉动压力系数最小,顶板中间区域的脉动压力系数最大。
从分离式双箱梁断面的平均压力系数和脉动压力系数结果可知,风攻角的变化导致上、下游断面脱落旋涡的影响区域发生了明显的改变,且敏感度各不相同,其中大攻角时变化最突出;上游断面迎风侧斜腹板和中央开槽区域来流旋涡分离再附作用随风攻角变化显著,尤其是下游断面迎风侧直腹板和斜腹板的脉动压力系数最大,说明迎风侧斜腹板和中央开槽区域断面的来流旋涡分离再附作用最强烈,且对风攻角尤其是大攻角敏感程度最明显。
2.2 局部特征区域气动力功率谱
下面针对上游断面的S-1区域以及下游断面的X-1区域和X-2区域(测点编号见表3)涡振最大振幅时的气动升力进行频谱分析。整个断面及不同区域的局部气动升力按照体轴方向上的气动升力FL(t)进行计算:
式中:δ为沿模型纵轴向宽度(此处取单位长度);Si为结构表面外轮廓i测点与相邻两测点中点间的距离(如图2所示);βi为i测点所在外轮廓线与体轴坐标系横坐标之间的夹角(逆时针方向,范围为0~2π);n为测点总数。
表4所示为风攻角为-5°~5°时分离式双箱梁模型不同局部特征区域上的气动升力及整个断面总气动升力功率谱密度(PSD)的特征参数。表4 中,FL(total),FL(S-1),FL(X-1)和FL(X-2)分别为主梁总体、上游断面S-1 区域、下游断面X-1 区域及下游断面X-2 区域的气动升力。根据表4 可知,下游断面X-2 区域对风攻角的敏感度比其他区域的高,因此,选取整体断面和X-2区域的气动升力频谱分析图进行展示。图9所示为相应的不同风攻角下气动力功率谱密度示意图。图9 中,Ptotal和PX-2分别为整体断面和X-2区域气动升力功率谱密度。
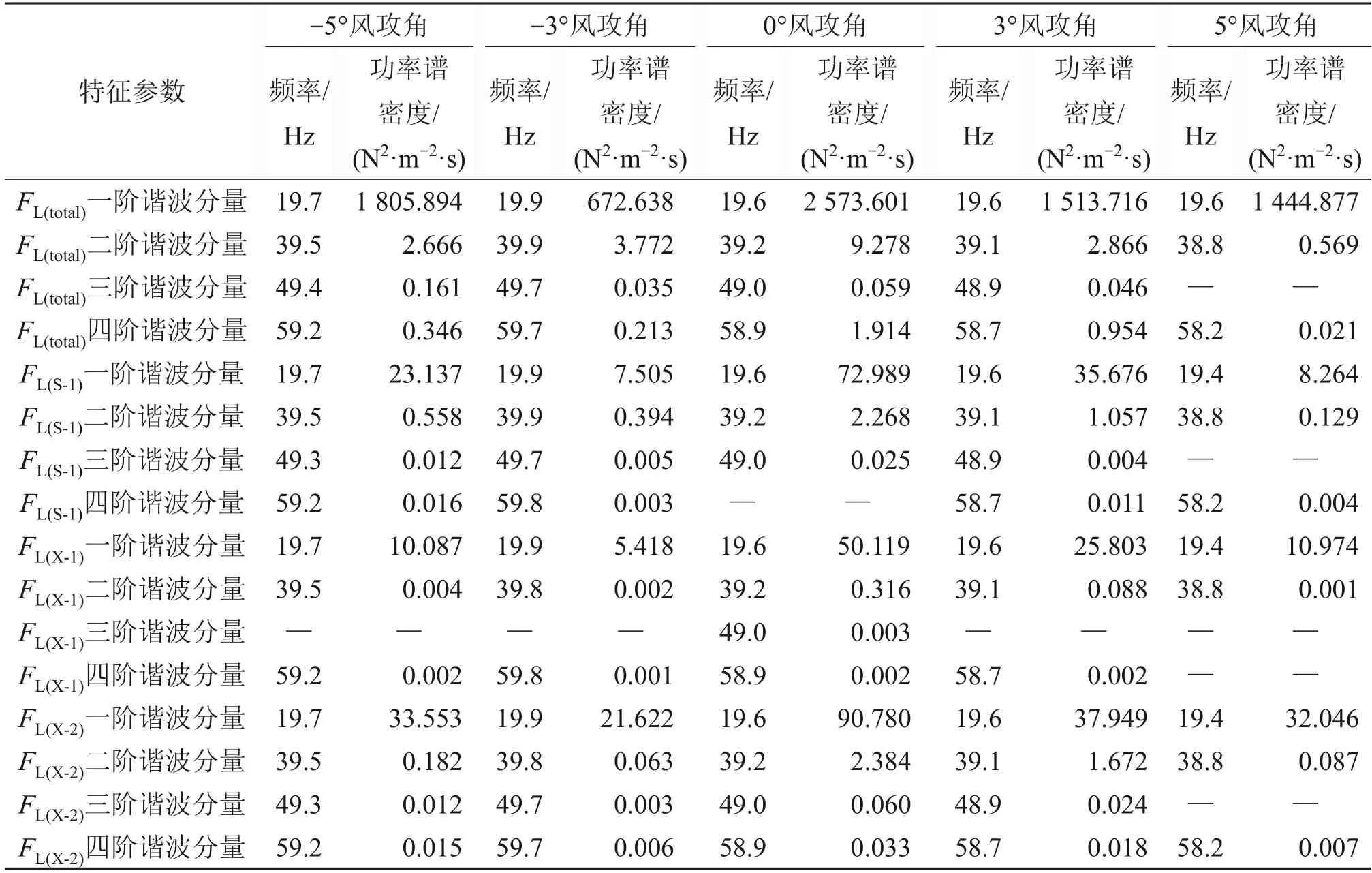
表4 不同风攻角下气动升力功率谱密度特征参数Table 4 Characteristic parameters of PSD for aerodynamic lift under different attack angles
由图9可以发现,在任一风攻角下第二涡振锁定区间最大振幅处,分离式双箱梁断面涡激力受结构运动状态控制,其总体气动升力及不同局部特征区域气动升力的卓越频率均在模型的竖弯自振频率19.6 Hz 附近,但是存在多个高阶谐波分量,这种倍频现象证明了气动力的非线性特性;另外,S-1 区域、X-1 区域及X-2 区域的气动升力卓越频率及二阶高阶谐波分量对应的频率均与断面的总体气动升力相应的频率一致,且不会随风攻角变化而改变。
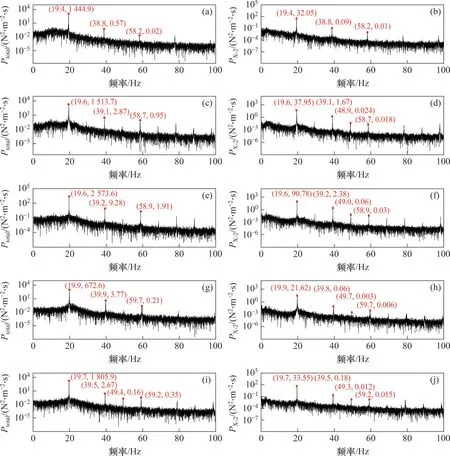
图9 不同风攻角下气动升力功率谱密度示意图Fig.9 Schematic diagram of aerodynamic lift PSD under different attack angles
随着风攻角的改变,卓越频率及其高阶谐波分量所对应的频率会稍有浮动,有些攻角下的(2n+1)/2 倍(n为大于等于1 的正整数)倍频效应发生改变。例如,总体气动升力在风攻角0°和3°下出现了卓越频率的1.5 倍倍频效应,但在风攻角-5°,-3°和5°下没有出现该效应,在风攻角-5°,-3°,0°和3°下出现了卓越频率的2.5 倍倍频效应,但是在5°风攻角下没有出现该效应。另外,整体断面及各局部特征区域气动升力卓越频率处及高阶谐波分量对应的功率谱密度随着风攻角变化而发生明显改变,高阶谐波分量对应的功率谱密度相对于卓越频率处功率谱密度普遍不高,可见涡激力非线性程度不高。在各风攻角下,X-2区域卓越频率处的功率谱密度明显比其他2 个区域的高,X-1区域除5°风攻角外其他卓越频率处的功率谱密度均最小,说明X-2 区域为涡振贡献的能量最大,X-1区域的能量最小;整体断面和各局部特征区域在风攻角0°和-3°下,卓越频率处气动升力功率谱密度分别达到最大值和最小值,与其他风攻角下的变化规律均不相同。
由此可知,在不同风攻角下,在第二竖弯涡振锁定区间振幅最大时,整体断面及各局部特征区域的气动升力卓越频率基本与结构运动频率保持一致;涡振力的各阶谐波分量对应频率参与涡振作用的比例不同;涡振力高阶谐波分量(2n+1)/2倍倍频效应所对应的频率不同。
3 局域气动力相关性
3.1 局域相关系数
为了进一步分析涡振发生时分离式双箱梁表面不同局部特征区域的气动力贡献,借鉴测点气动力相关性的概念[25-26],提出局部区域气动力与总体气动力之间的局域相关性概念,其相关系数可反映两者的频率和相位特征。本文以气动升力为例,给出相应的局域相关系数ρ的计算公式:
式中:FL(t)和Fi(t)分别为整体断面及某局部特征区域受到的气动力;σFL(t)和σFi(t)分别为整体断面气动力及某局部特征区域气动力根方差。局域相关系数ρ的取值范围为[-1,1],相关系数正值表示正相关,负值表示负相关,相关系数绝对值越大说明相关性越强。
图10所示为-3°风攻角下第二涡振锁定区间涡振振幅最大时X-1 区域和S-1 区域气动升力时程与整体断面气动升力时程的对比。由图10 可知气动升力并非单频的正弦曲线,且幅值有一定波动;相比于S-1 区域,X-1 区域气动升力脉动与总体气动升力脉动时程周期分布吻合程度较好。
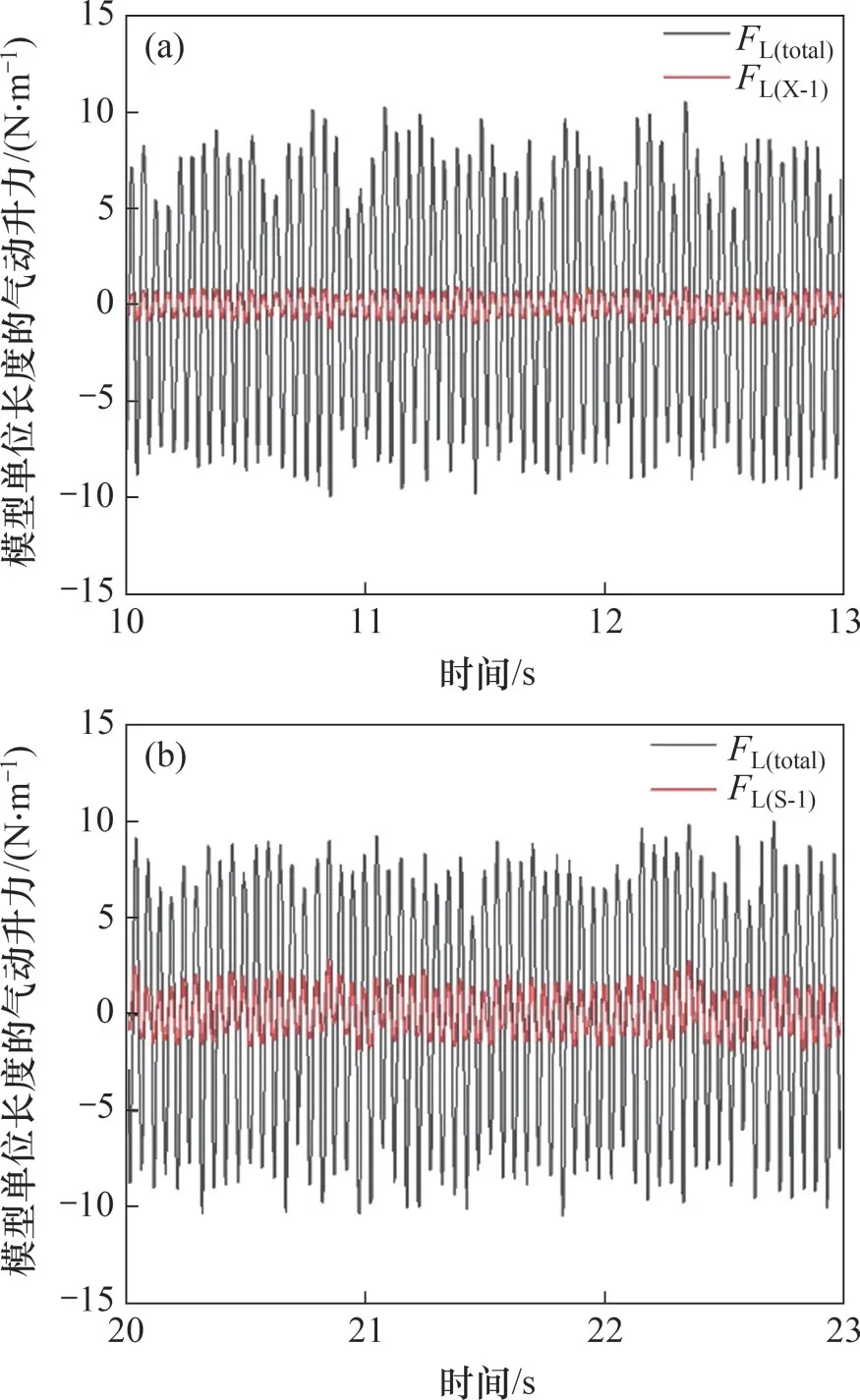
图10 -3°风攻角下涡振振幅最大时气动升力时程对比Fig.10 Time history comparison at maximum ⅤIⅤamplitude point under attack angle of -3°
图11所示为不同风攻角下分离式双箱梁涡振时表面不同局部特征区域的局域相关系数。由图11可知:在不同风攻角下发生最大涡振振幅时,X-1区域的气动升力与总气动升力的相关系数基本上都在0.9 左右,-3°和-5°风攻角下X-2 区域的气动升力与总气动升力的相关系数都大于0.8,说明局域气动升力与断面总气动升力相关性很好,可能对涡振的产生作出主要贡献;S-1 区域和X-2 区域随风攻角变化的规律正好相反,说明不同风攻角下分离式双箱梁发生涡振时,S-1区域气动力对总气动力的影响规律与X-2区域的正好相反;各区域相关系数差异较大,在风攻角为3°和-3°时相关系数达到极值。

图11 不同风攻角下局域相关系数Fig.11 Local correlation coefficient under different attack angles
3.2 局域气动力贡献系数
箱梁表面测点压力脉动及其与涡激力的相关性共同决定了主梁表面测点所受气动力对涡振的贡献度[25-28]。分离式双箱梁表面局部特征区域所受气动力对涡激力的贡献值CR可以表示为
式中:Ci,rms为主梁某局部特征区域内i测点的脉动压力系数;ρi(FL,Fi)为对应区域i测点所受气动力与总气动力的相关系数;m为某局部特征区域内测点总数。
图12所示为分离式双箱梁S-1,X-1和X-2这3个区域在不同风攻角下的局域气动力贡献系数。由图12 可以发现,各风攻角下X-1 区域的贡献系数相比于其他2 个局部特征区域的大且均为正值,即下游断面的内侧斜腹板区域的气动力对涡激力的增强效应最显著,增强作用按从大到小排列时对应的工况分别为风攻角-3°,-5°,5°,0°和3°。除5°风攻角工况外,在涡振幅值最大处,X-1区域气动力对涡激力的贡献随风攻角的变化趋势与涡振振幅和压力脉动的变化趋势基本一致,说明三者有明显的相关性。S-1区域在各风攻角下所受气动力对涡激力的贡献系数相差不大,相比于其他两个局部特征区域其贡献系数最小。除-5°风攻角工况外,在涡振幅值最大处,S-1区域气动力对涡激力的贡献随风攻角的变化趋势与平均压力的基本一致,说明两者有明显的相关性。另外,在风攻角-3°和0°工况时贡献系数为负,说明在风攻角-3°和0°下S-1区域会对涡激力产生抑制作用。X-2区域在各风攻角下所受气动力对涡激力的贡献系数相差也不大,在涡振幅值最大处,X-2区域气动力对涡激力的贡献随风攻角的变化趋势与平均压力的变化趋势正好相反,说明两者有明显的负相关性。
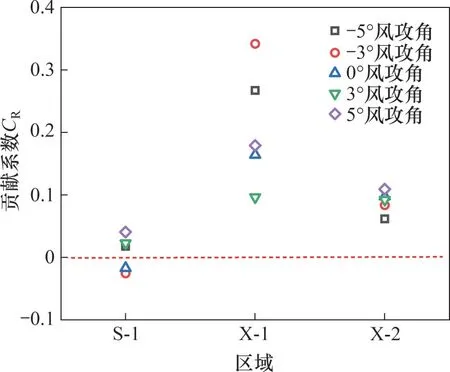
图12 不同风攻角下局域气动力贡献系数Fig.12 Contribution coefficient of local aerodynamic force under different attack angles
综合来看,本文所考虑的S-1 区域与X-2 区域在负风攻角时所受气动力对断面整体涡振的贡献小于其在正风攻角时的贡献,而X-1区域在正风攻角时所受气动力对断面整体涡振的贡献小于其在负攻角时的贡献;除-5°风攻角工况外,X-2 区域与S-1区域随风攻角的涡激力贡献系数变化规律与平均气动压力密切相关;除5°风攻角工况外,X-1区域随风攻角的涡激力贡献系数变化规律则与压力脉动和最大涡振振幅密切相关。
4 结论
1)分离式双箱梁发生竖弯涡振时迎风侧斜腹板和中央开槽区域断面的来流旋涡分离再附作用最强烈,且对风攻角尤其是大攻角工况最敏感。
2)在不同风攻角下,整体断面及各局部特征区域的气动升力卓越频率基本与结构运动频率保持一致,但参与涡振的各阶谐波分量的占比及高阶谐波分量(2n+1)/2倍倍频效应所对应的频率发生了改变。
3)不同局部特征区域气动力与总体气动力的相关性及其对整体涡激力的贡献随风攻角的变化规律各不相同,尤其在5°和-5°大攻角时变化突兀,其中,下游断面迎风侧斜腹板(X-1 区域)所受气动力与总气动力有着非常高的相关性,涡激力的贡献随风攻角(除5°风攻角工况外)的变化规律与压力脉动和最大涡振振幅密切相关,是发生涡振的一个重要原因。

