直线翼垂直轴风力机叶片支架对气动性能的影响

张艳锋，郭志平，朱新宇，张立军，蔡畅，李庆安

(1.内蒙古工业大学 机械工程学院，内蒙古 呼和浩特，010051；2.中国石油大学(华东)机电工程学院，山东 青岛，266580；3.中国科学院 工程热物理研究所，北京，100190)

近年来随着社会的高速发展，能源与环境的和谐显得十分重要。为了改善气候环境，我国提出了碳达峰、碳中和的承诺。电力脱碳与零碳化成为了关注的重点[1]。风能作为清洁型能源，会为碳中和这一目标做出贡献。由于垂直轴风力机对湍流敏感度低，适用在低风速，湍流强度较高的城市以及山区[2]，这为分布式风能资源的开发利用提供了一种选择。

近年来，CFD 仿真技术具有变量控制容易、成本相对较低、用时较短等特点，许多研究人员应用CFD 仿真技术作实验的预测、补充，或者直接应用CFD 仿真技术作项目研究。LI 等[3]通过风洞试验与CFD 仿真技术对垂直轴风力机的截面压力系数、单叶片转矩系数、叶片各截面转矩系数以及功率系数等参数进行研究，阐述垂直轴风力机的气动特性。郭志平等[4]通过CFD仿真技术与实验相结合来研究垂直轴风力机非定常流场速度特性。WANG 等[5]通过CFD 仿真技术与实验相结合来研究不同系列翼型对垂直轴风力机的影响。REZAEIHA 等[6-9]应用CFD 仿真技术研究回转轴、运行条件(叶尖速比、雷诺数、湍流强度)、攻角等因素对垂直轴风力机气动特性的影响，并且在不同叶尖速比与不同实度的条件下探究方位角增量、数值区域大小和收敛规律等因素对垂直轴风力机的影响。YANG 等[10]通过实验与CFD 仿真技术讨论了垂直轴风力机叶片最佳安装角为6°，并且基于Q 准则对垂直轴风力机产生的涡进行研究，得出涡位置对风力机尾流恢复有一定程度的影响。LEI等[11]利用三维数值模拟研究了垂直轴风力机的工作特性，发现从气动特性、流场特性和涡分布等方面的研究对预测风力机功率性能更为准确。ZHANG等[12]通过CFD仿真技术与风洞实验对垂直轴风力机的翼展方向的气动特性进行研究，发现垂直轴风力机气动性能会随翼展方向增加而下降，并且随叶尖速比增加，叶尖位置的气动性能下降得越严重。

在上述研究中，为了简化数值仿真模型，未添加叶片支架，未考虑叶片支架对风力机气动性能的影响。虽然支架的形状以及安装位置多样，但要得到更准确的直线翼垂直轴风力机性能预测结果，应进一步确认支架对垂直轴风力机的影响。针对叶片支架对直线翼垂直轴风力机气动性能的影响问题，使用SSTk-ω湍流模型对垂直轴风力机的气动性能和流场进行预测分析，并为后续的垂直轴风力机结构设计、性能优化和外场测试提供参考。

1 垂直轴风力机结构与气动参数

1.1 垂直轴风力机基本结构

直线翼垂直轴风力机基于空气动力学原理，选择与飞机叶片相似的翼型，使风轮机的输出性能在旋转时不会因变形而改变。垂直轴风力机主要由风轮、发电系统、制动系统和辅助系统组成。风力涡轮机的风轮由2～5个直叶片、连接叶片的支架和一个中间旋转轴组成，如图1所示。风轮在来流风速作用下驱动稀土永磁发电机发电并传输至控制器，实现电能的传输和分配。叶片支架作为风力机叶片的主要支撑部件，其具有良好的气动性能是保证风力机输出性能的关键。

图1 直线翼垂直轴风力机Fig.1 Straight-bladed vertical axis wind turbine

图2(a)所示为双叶片垂直轴风力机风轮简化模型的轴测图，风轮模型直径D=2.0 m，翼展高度H=1.2 m，叶片采用标准对称翼型NACA 0021，其弦长c=0.265 m，支架位于叶片中心偏移0.315 m处(支架中心截面用z=315 mm表示)，安装角为6°，截面长×宽为0.045 m×0.025 m的矩形支架。图2中笛卡尔坐标系为风轮的绝对坐标系，x轴正方向为自由风速方向，y轴为垂直于来流方向，z轴为叶片翼展方向，O点位置在风轮中心位置。图2(b)所示为垂直轴风力机风轮的俯视图，其回转方向顺时针为正，当叶片处于风轮最下端时，叶片的方位角为θ=0°。自由来流风从左到右吹过风轮，并将流场分为上流域(x＜0)和下流域(x＞0)2个区域。

图2 垂直轴风力机模型Fig.2 Model of vertical axis wind turbine

1.2 风力机气动参数

雷诺数是垂直轴风力机运行中的重要气动参数，其与来流风速的关系式为

式中：Re为雷诺数；U0为来流风速，m/s；c为翼弦长，m；v为运动黏性系数，m2/s。

叶尖速比λ为

式中：ωθ为叶片角速度，rad/s；R为风轮半径，m。

功率系数Cpower是衡量风力机输出性能的重要参数，其公式如下：

式中：Q为转矩，N·m；ρ为空气密度，kg/m3。

叶片表面压力系数CP公式如下：

式中：P为叶片表面压力，Pa。

2 湍流模型与数值模型

2.1 湍流模型

通过式(1)求出的雷诺数均比临界雷诺数大，风力机周围气流的流动状态以湍流为主[13]，故应选择湍流模型进行CFD 仿真。由于SSTk-ω湍流模型合并了来源于湍流频率ω方程中的交叉扩散，考虑到湍流剪应力的传播，所以该模型具有良好的稳定性、收敛性、对数层内压力梯度流动计算精确性与自由来流的湍流度不敏感性，并通过BANGGA 等[14]验证了SSTk-ω模型的计算结果较为准确。所以湍流模型采用的是雷诺时均湍流模型中的SSTk-ω模型。

该模型假定湍流黏性µt和湍流动能k以及湍流频率ω，其关系如下：

式中：k为湍流动能；ω为湍流频率。

湍流动能k方程为

式中：µ为时均速度；µ1为湍动黏度；δ为“Kronecherdelta”符号；Pk为湍动能k的生成项；β为湍动能k的耗散系数；k3为湍动能k的扩散系数。

湍流频率ω方程：

2.2 数值模型

模型采用结构网格，并通过组合网格的形式建立。图3所示为垂直轴风力机CFD 仿真的数值模型，在整体模型中，其模型沿x轴方向的长度为20D，沿y轴方向的宽度为10D，沿z轴方向的高度为2H，坐标原点位于风力机风轮的回转中心。在风轮附近的网格域中，由于风轮附近的风速和压力变化梯度较大，对风轮附近的网格进行了加密处理。模型应用滑移网格技术，将值模型分为动网格(move mesh)和静网格(static mesh)。在叶片附近的被进一步加密的网格和边界层网格中，雷诺数Re=2.89×105，第一层边界厚度为0.02 mm，增长因子为1.1，满足边界层条件y+＜1(y+为量纲一的壁面距离)，文献[15]也使用相同的边界层厚度和边界层条件。

图3 垂直轴风力机CFD仿真的数值模型Fig.3 Numerical model of CFD simulation of vertical axis wind turbine

采用速度入口边界条件，入口风速U0=8 m/s，湍流强度0.5%；出口采用压力出口边界条件；回转区域交界面采用interface边界条件，回转区域速度满足叶尖速比λ=2.19；回转轴、叶片以及叶片支架采用无滑移壁面条件。

3 结果分析

3.1 单叶片功率系数曲线

由于支架形状以及安装位置都有特殊性，风力机叶片翼展方向中间位置周围流场受叶尖涡、展向气流和支架影响较小，因此，选择通过将模型简化为无支架的CFD 仿真计算所得叶片中间截面(z/R=0)的局部功率系数，并将其与来自文献[16]的实验数据进行对比，验证CFD 仿真的有效性，如图4所示。由图4可以看出：单叶片功率系数在趋势上符合实验结果，其中在方位角为50°＜θ＜210°的上流域区间仿真效果较好。然而，在其他方位角处，叶片主要处于风轮的下流域，由于上流域紊乱气流的影响使得下流域气流运动非常复杂，致使数值仿真模型与文献[16]中的实验值出现偏差。此外，风洞实验中风力机回转轴的空气阻力和驱动系统的机械损耗是导致这种差异的另外2个原因。同时，数值仿真和风洞实验之间的相对差值与模拟过程中的许多模型因素有关，如简化的物理模型、湍流模型、网格质量和能量损失[17-18]。虽然CFD 仿真数值稍有偏差，但总体而言还是有一定的可信度，因此，CFD 仿真模型可用于后续计算分析。

图4 单叶片局部功率系数仿真结果与实验结果对比Fig.4 Comparison of local power coefficient of single blade between CFD simulation and experimental data

为了研究叶片支架对风力机气动特性的影响，将无支架模型的单叶片功率系数与有支架模型的单叶片功率系数进行对比，分析叶片支架对风力机功率系数的影响规律，如图5所示，由图5 可知：无支架模型计算出的单叶片功率系数与有支架模型计算出的单叶片功率系数在整体趋势上保持一致。支架的回转运动，致使风轮内部的气流随着风轮的运动趋势加剧，造成下流域195°＜θ＜250°区间有支架模型的单叶片功率系数提高。除195°＜θ＜250°外，其余方位角有支架模型的单叶片功率系数均比无支架模型计算出的单叶片功率系数的小，并且可以看出在方位角θ=110°时，有支架模型对于单叶片功率系数的最大值影响较大，最大值下降约47.5%。

图5 单叶片功率系数曲线Fig.5 Power coefficient curves of single blade

3.2 叶片压力云图

将无支架模型与有支架模型叶片压力云图进行对比，如图6所示，其中截面1，2和3依次为无支架模型叶片的内侧面、前缘面和外侧面，截面4，5和6依次为有支架模型叶片的内侧面、前缘面和外侧面。由图6可知：支架的存在对气流产生阻碍与分流，使图6(a)中6 截面、图6(b)中4 截面、图6(c)中4 截面与图6(d)中4 截面的叶片前缘负压区域减少，正压区域变化较小，压差下降，功率系数减小；支架的存在使图6(e)中的4截面的压力正值稍有增大，使6截面的压力负值区增大，增加压差，使功率系数比无支架模型的功率系数高。

3.3 截面压力系数

为了进一步研究叶片支架对垂直轴风力机叶片压力的影响，取叶片z=0 mm 截面与z=315 mm截面的压力系数进行对比，得到叶片支架对叶片截面压力系数的影响，如图7所示。

图 6 叶片表面压力云图Fig.6 Pressure nephograms of blade surface

由图7可知：对比无支架模型与有支架模型在z=0 mm 截面压力系数，发现无支架模型叶片前缘压力差比有支架模型叶片前缘压力差的大，但变化趋势相同；z=315 mm 截面由于支架对气流的影响，导致叶片前缘压力差变小，气动性能降低，使在方位角θ=0°，60°，120°，180°和300°时，无支架模型叶片的功率系数比有支架模型叶片的功率系数大；支架存在还会小幅度提高叶片中部到尾缘的压力差。在θ=240°时，由于叶片前缘压力差相同，有支架模型的叶片中部到尾缘的压力差较大，使有支架模型的压力系数比无支架模型的压力系数大。

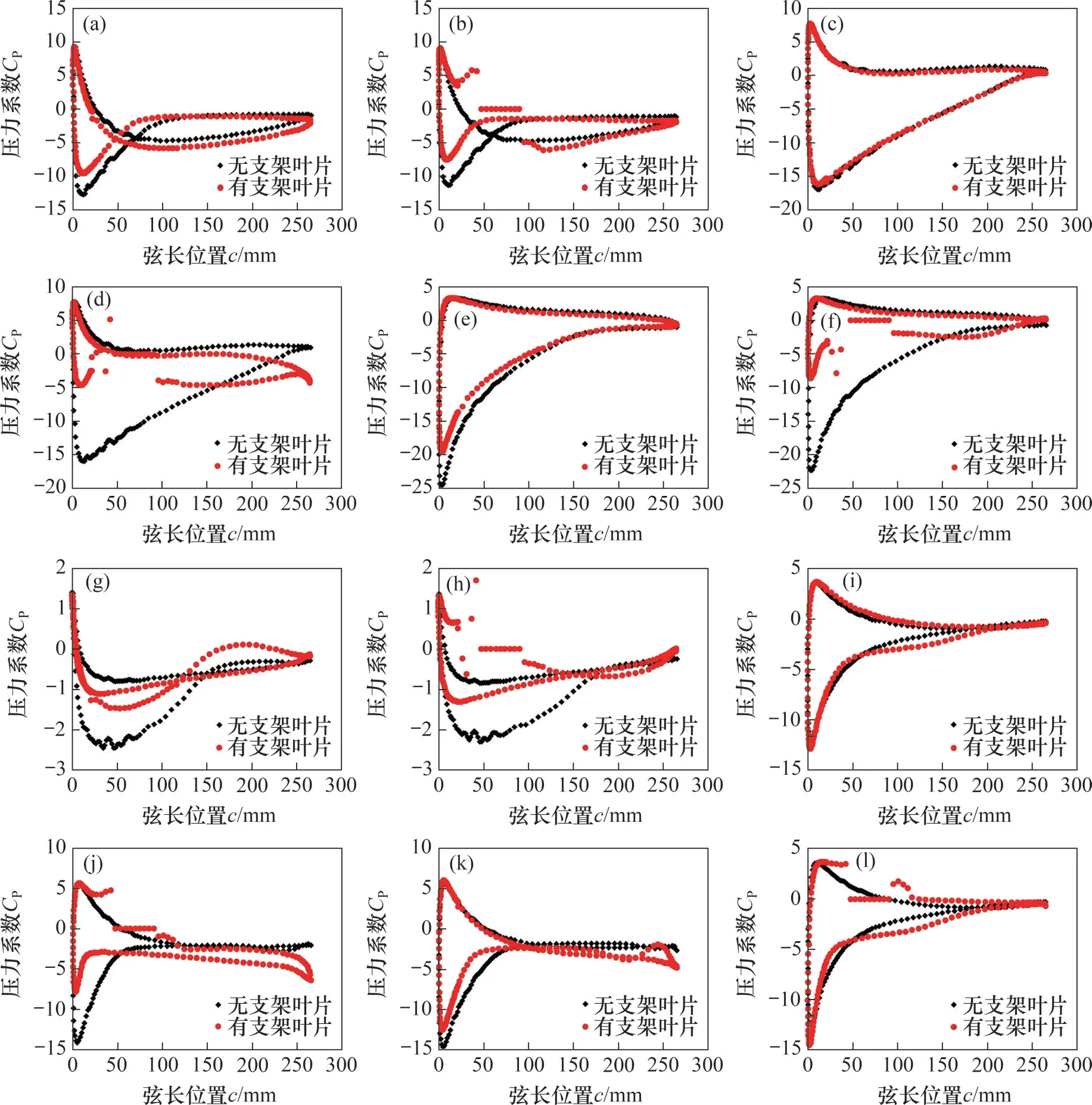
图7 叶片截面压力系数Fig.7 Pressure coefficient of blade section

3.4 流场分析

流场特性对于风力机性能十分重要。图8所示为垂直轴风力机下流域风速云图。

由图8 可知：风轮的低风速区域不是关于x轴对称分布，其低风速区域偏向于方位角270°＜θ＜90°侧，其主要由风轮的回转方向所致。当模型相同时，z=0 mm截面产生的低风速区域比z=315 mm截面的更广，这说明在不考虑其他因素的情况下，叶片z=0 mm截面产生压力差会更大，得到的功率系数会更高，这在图7中也可以体现；在无支架模型产生的低风速(＜3 m/s)区域中风速较低，并且在无支架模型的低风速(4 m/s)区域比有支架模型的低风速区域大；支架在旋转过程中对周围气流的阻碍与分流，使其周围形成的低风速区域更大，导致在多数情况下有支架模型的叶片前缘压差下降，尤其是位于支架附近的位置。

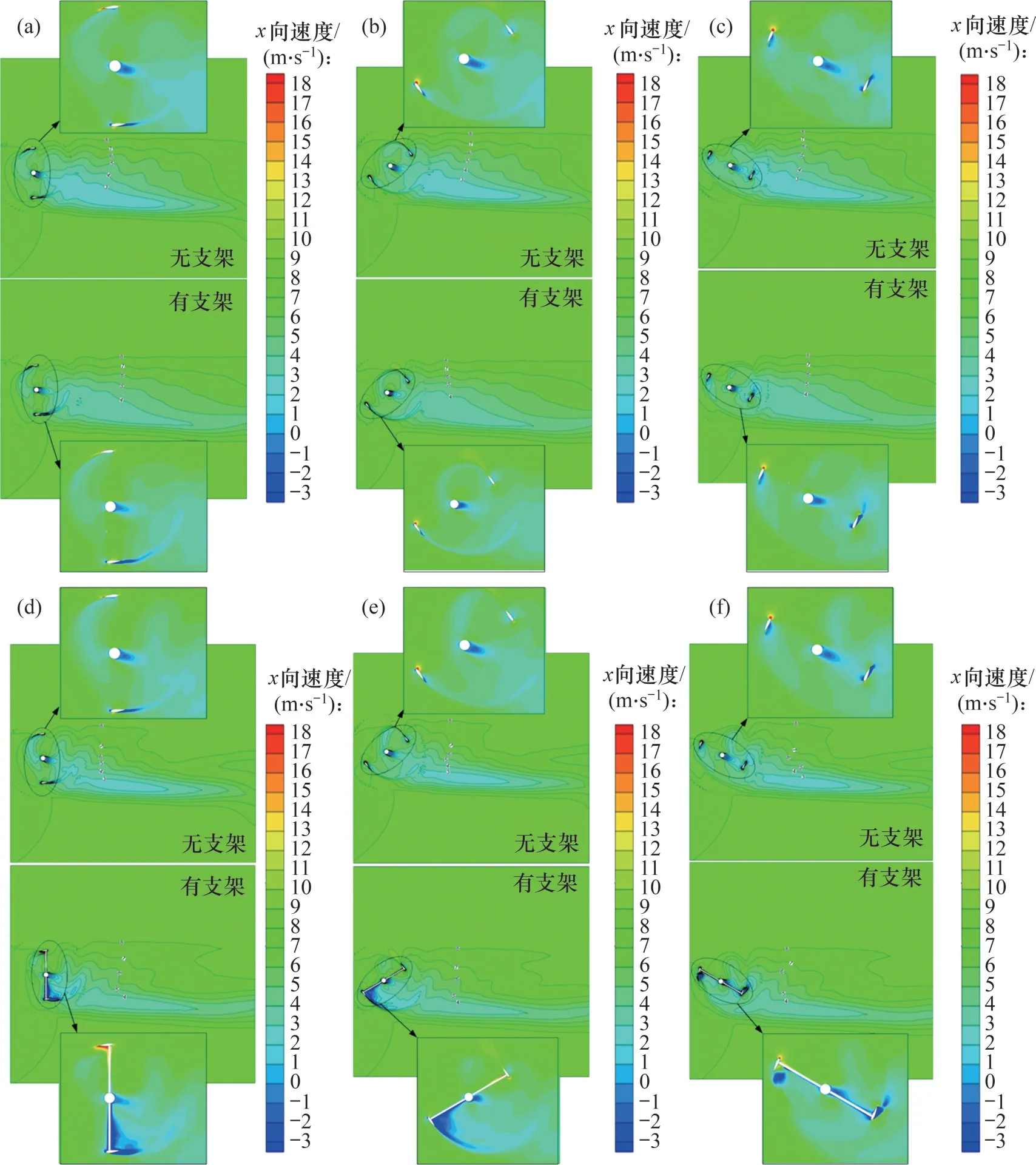
图8 垂直于z轴风速云图Fig.8 Wind velocity nephogram perpendicular to z-axis

图9所示为垂直轴风力机垂直于x轴的风速云图。由图9 可知：无支架模型与有支架模型在x/R=0处由于支架对流场的影响使靠近支架位置出现低风速区域，但在x/R=-1，1，2，4 和8 处无支架模型与有支架模型的风速分布相似；对比x/R=4和8处的风速云图，有支架模型风速恢复速度比无支架模型的慢。

图9 垂直于x轴风速云图Fig.9 Wind velocity nephogram perpendicular to x-axis

3.5 风速曲线

为定量的分析风数值的规律，建立风速曲线。在方位角为θ=0°、60°、120°在z=0 mm 截面与z=315 mm截面的风速如图10所示。由图10可知：在y轴方向上，取-2＜y/R＜2区间上的风速进行分析。根据图2(b)和图3(b)可以看出，在x/R=0 和y/R=0位置是风力机回转轴的回转中心，回转轴的直径为0.15 m，因此在数值仿真结果中，在x/R=0 和y/R=0 位置的风速为0 m/s。在垂直于来流风速的z轴方向上，取全部翼展方向上风速的平均值。当x/R=4时，风轮下流域的风速达到最小值，并且无支架风速最小值更低，区域更广；当x/R=8时，无支架模型风速比有支架模型风速高，说明无支架模型风速恢复较快；在z=0 mm截面有支架模型与无支架模型风速曲线趋势相同；在z=315 mm截面由于支架与支架回转造成有支架模型在x/R=0处出现风速最低值以及大区域风速低值。

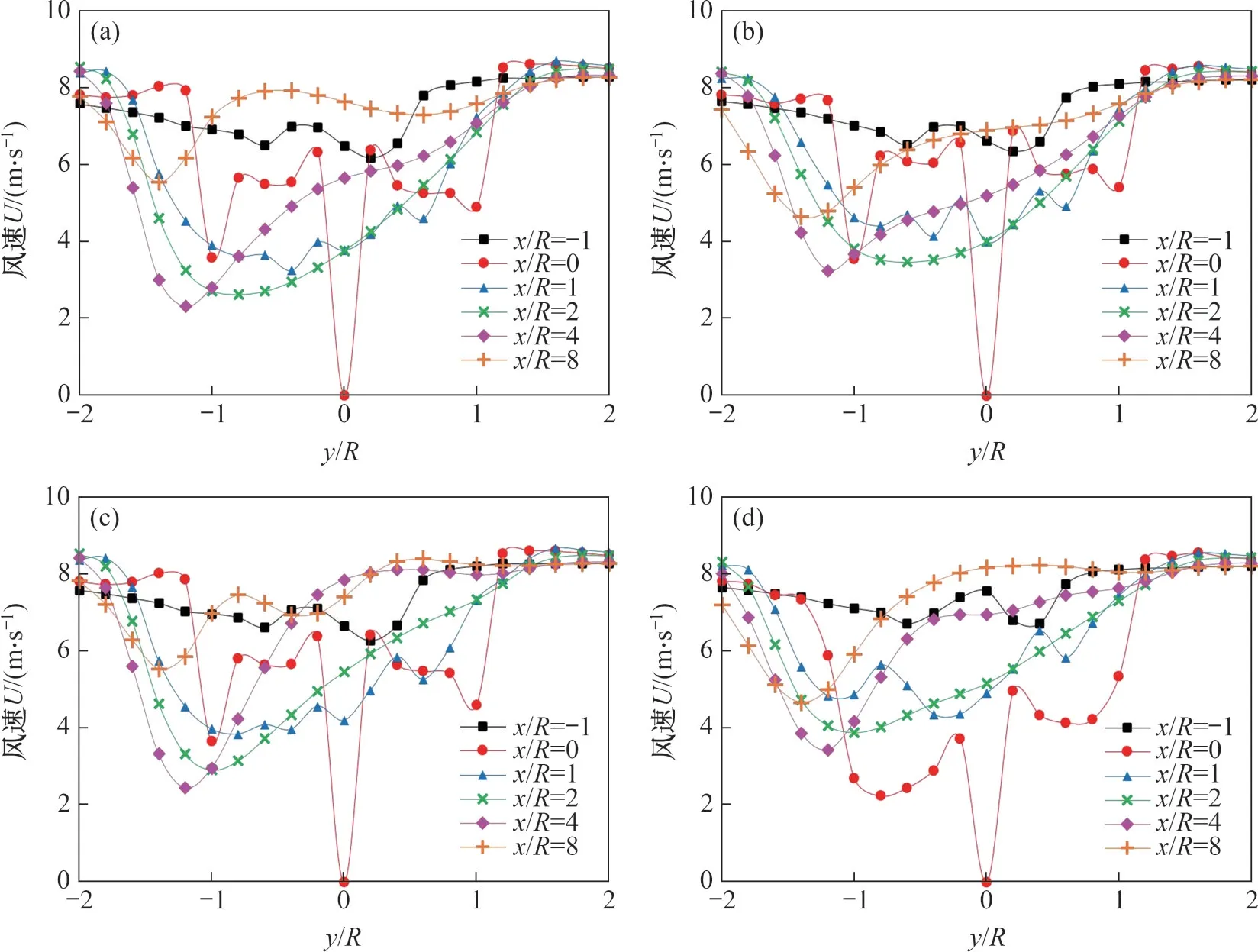
图10 风速曲线Fig.10 Wind velocity curves

提取出θ=0°，θ=60°和θ=120°时沿翼展风向速度，再求风速的平均值，如图11所示。由图11 可知：沿y轴方向的风速先逐渐减小再增加，当x/R=4.0 时，下流域的风速达到最小值；当x/R=8.0 时，由于与自由流能量交换的作用，此处的风速恢复，其中无支架模型平均风速恢复到流风速的91%，最低风速恢复到来流风速的73%，有支架模型平均风速恢复到流风速90%，最低风速恢复到来流风速的64%，可见有支架模型风速恢复相对较慢。

图11 平均风速曲线图Fig.11 Ⅴelocity curves of average wind

4 结论

1)支架的回转扰动使风轮内部的气流随着风轮的运动趋势加剧，在下流域195°＜θ＜250°区间有支架模型的单叶片功率系数提高，而在其他方位角有支架模型的单叶片功率系数均比无支架模型功率系数小，有支架模型的单叶片功率系数在方位角θ=110°下降约为47.5%。

2)在风力机叶片z=0 mm截面中无支架模型与有支架模型压力差区别较小且趋势相同，在z=0 mm截面前缘压差最大；在叶片z=315 mm截面，支架会使风力机叶片前缘压力差下降，同时使叶片中部到尾缘的压力差稍有增加，因此风力机叶片支架位置应远离z=0 mm截面。

3)随着x/R的增大，低风速区的面积逐渐扩大，其值先减小后增大。当x/R=4.0 时，下流域的风速达到最小值，有支架模型比无支架模型产生的风速最小值更高，且有支架模型风速恢复速度相对较慢。